Abstract
Bessel beams are of great interest due to their unique non-diffractive properties. Using a conical prism or an objective paired with an annular aperture are two typical approaches for generating zeroth-order Bessel beams. However, the former approach has a limited numerical aperture (NA), and the latter suffers from low efficiency, as most of the incident light is blocked by the aperture. Furthermore, an additional phase-modulating element is needed to generate higher-order Bessel beams, which in turn adds complexity and bulkiness to the system. We overcome these problems using dielectric metasurfaces to realize meta-axicons with additional functionalities not achievable with conventional means. We demonstrate meta-axicons with high NA up to 0.9 capable of generating Bessel beams with full width at half maximum about as small as ~λ/3 (λ=405 nm). Importantly, these Bessel beams have transverse intensity profiles independent of wavelength across the visible spectrum. These meta-axicons can enable advanced research and applications related to Bessel beams, such as laser fabrication, imaging and optical manipulation.
Similar content being viewed by others
Introduction
Non-diffracting Bessel beams are a set of solutions of the free space Helmholtz equation and have transverse intensity profiles that can be described by the Bessel functions of the first kind. Since their discovery in 19871, they have exhibited many interesting properties such as non-diffraction1, self-reconstruction2 and even providing optical pulling forces3, 4. The scalar form of Bessel beams propagating along the z axis can be described in cylindrical coordinates (r,φ,z) by:

where A is the amplitude, kz and kr are the corresponding longitudinal and transverse wavevectors that satisfy the equation  (where λ is the wavelength). Equation (1) shows that the transverse intensity profiles of Bessel beams are independent of the z coordinate, which gives rise to their non-diffracting characteristic. It also indicates that any higher-ordered Bessel beam (n≠0) must carry orbital momentum and have zero intensity along the z axis at r=0 because of the phase singularity resulting from the
(where λ is the wavelength). Equation (1) shows that the transverse intensity profiles of Bessel beams are independent of the z coordinate, which gives rise to their non-diffracting characteristic. It also indicates that any higher-ordered Bessel beam (n≠0) must carry orbital momentum and have zero intensity along the z axis at r=0 because of the phase singularity resulting from the  term.
term.
Ideal Bessel beams are not spatially limited and carry infinite energy; therefore, they can only be approximated within a finite region by the superposition of multiple plane waves. This can be achieved by symmetrically refracting incident plane waves toward the optical axis of a conical prism, an axicon, to generate a J0 Bessel beam. Figure 1a shows the schematic diagram of a conventional axicon. The numerical aperture (NA) of an axicon is related to the angle α (Figure 1a) by:

where n is the refractive index of the constituent material, often glass. This equation and Figure 1a show that for a given refractive index, achieving high NA axicons requires an increase in α. Considering a refractive index of 1.5, typical of most silica glasses, total internal reflection occurs when α>42°. Thus, the NA of a conventional axicon cannot exceed 0.75 (Supplementary Fig. S1). This, in turn, also limits the minimum achievable full width at half maximum (FWHM) of the Bessel beam. In addition, the tip of a refractive axicon is rounded instead of being perfectly sharp because of limitations in glass polishing, which again affects the FWHM of the Bessel beam5. Herein, the FWHM of the zeroth-order Bessel beam J0 is defined as the distance between two points at half of the maxima intensity of the center bright spot, and can be derived from Equation (1) as:

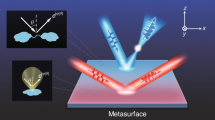
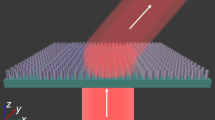
Comparison of conventional axicons with meta-axicon. (a, b) Schematic diagram of two conventional approaches for generating a J0 Bessel beam. (a) Cross-section of a conventional refractive axicon comprised of a glass prism. The axicon angle α and the refraction angle θ, which determine the NA, are labeled. (b) A high NA objective paired with an annular aperture for generating a J0 Bessel beam. (c) Schematic diagram of a meta-axicon. The meta-axicon deflects an incident collimated light to an angle θ toward its center to generate Bessel beams. The meta-axicon is composed of identical TiO2 nano-fins but different rotation angle θnf with respect to its geometrical center. Two different meta-axicons with NAs of 0.9 and 0.7 are designed at wavelengths λ=405 and 532 nm with corresponding dimensions (L=125 nm, W=60 nm, h=600 nm, P=155 nm) and (L=210 nm, W=65 nm, h=600 nm, p=250 nm). (d) A scanning electron microscope micrograph of a fabricated meta-axicon. Scale bar=1 μm.
where  . Similarly, the FWHM of a J1 Bessel beam is defined as twice the distance from the dark spot center to the point at its closest ring with the half maxima intensity, and given by:
. Similarly, the FWHM of a J1 Bessel beam is defined as twice the distance from the dark spot center to the point at its closest ring with the half maxima intensity, and given by:

In the case of conventional axicons, the NA is almost constant within the visible region due to the weak dispersion of glass. Thus, the FWHM of the J0 beam is proportional to wavelength and varies accordingly. For example, changing the wavelength from 400 to 700 nm can result in a difference of 175% in the FWHM. Alternatively, a high NA objective lens paired with an annular aperture is usually used to generate Bessel beams with subwavelength FWHMs6, as shown in Figure 1b. However, this configuration is not efficient as most of the incident light is blocked by the aperture. Both methods require the addition of phase-modulating elements, such as spatial light modulators or spiral phase plates, to generate higher-ordered Bessel beams.
In recent years, metasurfaces, consisting of subwavelength-spaced phase shifters, have been demonstrated to fully control the optical wavefront7, 8, 9, 10, 11, 12. Various compact optical components have been reported including lenses13, 14, 15, 16, 17, holograms18, 19, 20, 21, modulators22, 23, 24 and polarization-selective devices25, 26, 27, 28. Metallic and dielectric metasurface axicons were reported in Ref. 29 and Ref. 27, respectively; both had low NAs. Unlike conventional phase-modulating devices (for example, spatial light modulators), metasurface-based devices can provide subwavelength spatial resolution, which is essential in order to deflect light by very large angles. This is mandatory to realize high NA optical components, including axicons and lenses capable of generating beams with even smaller FWHM. Various applications, including (but not limited to) scanning microscopy6, 30, 31, optical manipulation32, 33, 34 and lithography35, 36, all require subwavelength FWHM to achieve high spatial resolution, strong trapping force and subwavelength feature sizes, respectively. Here we report meta-axicons with high NA up to 0.9 in the visible region that are capable of generating, not only the zeroth-order, but also higher-ordered Bessel beams with FWHM about one-third of the wavelength without the use of additional phase elements. In addition, by appropriately designing the metasurfaces’ phase shifters, the transverse field intensity profiles are maintained independent of the wavelength.
Materials and methods
Figure 1c shows a schematic diagram of a meta-axicon. The basic elements of the meta-axicon are identical rotated titanium dioxide (TiO2) nano-fins with height h, length L and width w, arranged in a square lattice. To maximize the performance of the meta-axicon, each nano-fin should act as a half-waveplate at the design wavelength, converting incident circularly polarized light to its orthogonal polarization state. To tailor the required phase profiles, we use geometric phase associated with the rotation angle of the nano-fin, known as the Pancharatnam–Berry phase37, 38. The h, L and w parameters are determined using the three-dimensional finite difference time domain (FDTD from Lumerical Inc.) method to maximize the circular polarization conversion efficiency39, 40. At the design wavelength λd=405 nm, simulated polarization conversion efficiencies >90% were obtained. The efficiencies decrease as NA increases due to the sampling criterion (Supplementary Fig. S2). To determine the polarization conversion efficiency, we arranged an array of TiO2 nano-fins in such a way to deflect light to a particular angle and then the efficiency is calculated by dividing the total deflected optical power by the input optical power. Perfectly matched layer boundary conditions were used normal to the propagation of the incident circularly polarized light and periodic conditions were used for the remaining boundaries.
For the generation of a zeroth-order Bessel beam, a meta-axicon requires a radial phase profile φ(r) with a phase gradient

This can be understood from the generalized Snell’s law9 as the condition for all light rays to be refracted by the same angle θ at the design wavelength λd, where sin(θ) is the NA. Integrating Equation (5) gives:

where  . The generation of the high-order Bessel beams requires the addition of a term nφ, where
. The generation of the high-order Bessel beams requires the addition of a term nφ, where  is the azimuthal angle, which represents the phase of an optical vortex imparted to the deflected light. Equation (6) then becomes
is the azimuthal angle, which represents the phase of an optical vortex imparted to the deflected light. Equation (6) then becomes

This phase profile is imparted by the rotation of each nano-fin at a position (x, y) by an angle  for the case of left-handed polarized incidence. TiO2-based meta-axicons are fabricated using the approach described in Ref.41, which can prevent tapered sidewall42. Figure 1d shows a scanning electron microscope image of the center part of a fabricated meta-axicon. We used a custom-built microscope to characterize the meta-axicons. A schematic diagram of the set-up and the optical components used can be found in Supplementary Fig. S3.
for the case of left-handed polarized incidence. TiO2-based meta-axicons are fabricated using the approach described in Ref.41, which can prevent tapered sidewall42. Figure 1d shows a scanning electron microscope image of the center part of a fabricated meta-axicon. We used a custom-built microscope to characterize the meta-axicons. A schematic diagram of the set-up and the optical components used can be found in Supplementary Fig. S3.
Results and discussion
Figure 2a and 2d shows the measured transverse intensity profile of the J0 and J1 Bessel beams at λ=405 nm, whereas Figure 2b and 2e shows the intensity along a horizontal cut across the centers of Figure 2a and 2d, respectively. The measured FWHM of the J0 Bessel beam is observed to be ~163 nm with 3.5 nm standard deviation, which is very close to its theoretical limit of 160 nm (Equation (3)). The measured FWHM of the J1 Bessel beam is 130 nm with 1.75 nm standard deviation, which agrees well with its theoretical value of 131 nm (Equation (4)). Figure 2c and 2f shows the intensity profile along the beam propagation direction of the J0 and J1 Bessel beams. Their FWHMs at different planes normal to the propagation z axis are provided in Supplementary Fig. S4. Both the J0 and J1 Bessel beam have a depth of focus of 75 μm (150λ). This value is close to the theoretical value using geometric optics, that is,  , where D=300 μm is the diameter of the meta-axicons.
, where D=300 μm is the diameter of the meta-axicons.
Optical characterization of meta-axicons with NA=0.9 designed at wavelength λd=405 nm. (a, b) Measured intensity profile (a) for the meta-axicon designed to generate J0 (scale bar=250 nm) and its corresponding horizontal cut (b). (c) Normalized intensity profile of the Bessel beam (J0) along the propagation direction. (d, e) Measured intensity profile (d) for the meta-axicon designed to generate J1 (scale bar=250 nm) and its corresponding horizontal cut (e). (f) Normalized intensity profile of the Bessel beam (J1) along the propagation direction.
Polarization properties of a Bessel beam generated by a high NA meta-axicon can be very different from that of a corresponding axicon with low NA43, 44. In order to understand the polarization properties of the J0 and J1 Bessel beams generated by the meta-axicons with NA=0.9, we show in Figure 3 their theoretical (first row) and simulated (second row) normalized electric field intensities |Ex|2, |Ey|2 and |Ez|2. Only a portion of the meta-axicon (30 μm in diameter), but with the same NA, was simulated due to limited computational resources. A slight deviation of the simulations from theory results from the uncoupled light of nano-fins and the effects of the boundary in the simulations. We note that for either |Ex|2 (Figure 3a and 3d) or |Ey|2 (Figure 3b and 3e), the shape of the J0 and J1 Bessel beams at their respective centers is elliptical rather than circular. For example, as shown in Figure 3d and 3e, for J1, the center regions are accompanied by two brighter spots at the end of the long axis of the ellipse. Moreover, the intensity of |Ex|2 and |Ey|2 show variation on their side lobes. These are also observed in their corresponding simulation results (Figure 3j and 3k). In addition, |Ez|2 is described by a Bessel function one order larger than its transverse electric field. These properties can be explained by considering the vector form of Bessel beams. The theoretical vector solutions of the electric field of a Bessel beam propagating along the z direction in cylindrical coordinates are:

Polarization properties of meta-axicons with NA=0.9 designed at wavelength λd=405 nm. A comparison of the square of the electric fields from theoretical calculation using Equation (8) (first row) and FDTD simulations (second row). The first (a, g), second (b, h) and third columns (c, i) show |Ex|2, |Ey|2 and |Ez|2 for the J0 Bessel beam, respectively. The corresponding plots for the J1 Bessel beam are shown on the right side of the black line. Scale bar=250 nm.
where CTM and CTE are complex numbers associated with the constituent transverse magnetic (TM) and transverse electric (TE) waves of Bessel beams, and η is the phase difference between CTM and CTE3, 45). For our case (circularly polarized Bessel beams), CTE is equal to CTM,  , NA=0.9, and n=0 and n=1 for J0 and J1 Bessel beam, respectively. For high NA Bessel beams, the electric field of the z component results from TM waves: the higher the NA, the higher the contribution the TM waves make to
, NA=0.9, and n=0 and n=1 for J0 and J1 Bessel beam, respectively. For high NA Bessel beams, the electric field of the z component results from TM waves: the higher the NA, the higher the contribution the TM waves make to  . The
. The  and
and  components mainly result from TE wave contribution, as the term
components mainly result from TE wave contribution, as the term  is relatively small for the high NA case. The term
is relatively small for the high NA case. The term  contributes to localized intensity near the center spot or the most inner ring, as
contributes to localized intensity near the center spot or the most inner ring, as  for large r, such that Jn(krr) and Jn+2(krr) cancel each other due to a π phase difference. The intensity distribution of side lobes away from the center of a Bessel beam is due to another term
for large r, such that Jn(krr) and Jn+2(krr) cancel each other due to a π phase difference. The intensity distribution of side lobes away from the center of a Bessel beam is due to another term  . When we transform cylindrical (r,φ) to Cartesian coordinates (x,y) using
. When we transform cylindrical (r,φ) to Cartesian coordinates (x,y) using  , we will have cos (φ) modulation resulting in the elliptical center, and a corresponding modulation of sin (φ) for the side lobe, which is shown in Figure 3a and 3d, respectively. This is a signature feature of high NA Bessel beams (see a comparison with a lower NA in Supplementary Fig. S5). Due to the spatially varying intensity of Ex and Ey, the Bessel beams for high NA are not homogeneously polarized, but rather show space-variant polarization states (see Supplementary Fig. S6 for plots of ellipticity and polarization orientation angle). Therefore, only the center part of the J0 Bessel beam can be circularly polarized in the case of high NA case.
, we will have cos (φ) modulation resulting in the elliptical center, and a corresponding modulation of sin (φ) for the side lobe, which is shown in Figure 3a and 3d, respectively. This is a signature feature of high NA Bessel beams (see a comparison with a lower NA in Supplementary Fig. S5). Due to the spatially varying intensity of Ex and Ey, the Bessel beams for high NA are not homogeneously polarized, but rather show space-variant polarization states (see Supplementary Fig. S6 for plots of ellipticity and polarization orientation angle). Therefore, only the center part of the J0 Bessel beam can be circularly polarized in the case of high NA case.
By the judicious design of our metasurface, we compensate the wavelength dependency of the FWHM of Bessel beams (Equations (3) and (4)). As mentioned previously, the transverse intensity profile is determined by the factor  . In our case, the
. In our case, the  , where φ follows Equation (7). Therefore, kr only depends on the phase gradient ∇φ(x,y,λ), which can be designed to be wavelength-independent using the Pancharatnam–Berry phase concept. In this case, the phase gradient is a constant, and the NA is only proportional to the wavelength λ. This manifests experimentally, in the form of the increasing ring diameters in the Fourier plane of the meta-axicons for increasing wavelength (Supplementary Fig. S7). To demonstrate this unique characteristic across a broad wavelength region, we use the same method to design two meta-axicons for J0 and J1 with the NA=0.7 at the wavelength λ=532 nm. Each nano-fin (L=210 nm, W=65 nm and h=600 nm) for this case is arranged in a square lattice, with a lattice constant of 250 nm. We show in Figure 4a–4d and 4f–4i the corresponding J0 and J1 Bessel beams in false color for different wavelengths (at λ=480, 530, 590 and 660 nm) with a bandwidth of 5 nm at the z plane about 60 μm away from the surface of meta-axicons. Note that the efficiency of the meta-axicon is dependent on wavelength. The efficiency was measured and is shown in Supplementary Fig. S8. The FWHMJ0 and FWHMJ1 for each wavelength spanning 470–680 nm are shown in Supplementary Fig. S9. Figure 4 explicitly indicates that the intensity profile for different wavelengths vary weakly, confirming wavelength-independent behavior. It is notable that for these measurements the distance between the meta-axicon and objective lens was kept unchanged. We also repeated the measurements using a supercontinuum laser of bandwidth 200 nm centered at 575 nm (see Supplementary Fig. S10 for its spectrum). The intensity profiles (Figure 4e and 4j) for both J0 and J1 remarkably changed weakly. It is important to note that in order to generate high NA and wavelength-independent Bessel beams, the Nyquist sampling theorem and wavelength-independent phase gradient conditions both need to be satisfied. According to the Nyquist sampling theorem, one needs to sample the phase profile given by Equation (7) in the spatial domain with a rate that is at least twice the highest transverse spatial frequency. This requires the size of the unit cell to be equal to or smaller than
, where φ follows Equation (7). Therefore, kr only depends on the phase gradient ∇φ(x,y,λ), which can be designed to be wavelength-independent using the Pancharatnam–Berry phase concept. In this case, the phase gradient is a constant, and the NA is only proportional to the wavelength λ. This manifests experimentally, in the form of the increasing ring diameters in the Fourier plane of the meta-axicons for increasing wavelength (Supplementary Fig. S7). To demonstrate this unique characteristic across a broad wavelength region, we use the same method to design two meta-axicons for J0 and J1 with the NA=0.7 at the wavelength λ=532 nm. Each nano-fin (L=210 nm, W=65 nm and h=600 nm) for this case is arranged in a square lattice, with a lattice constant of 250 nm. We show in Figure 4a–4d and 4f–4i the corresponding J0 and J1 Bessel beams in false color for different wavelengths (at λ=480, 530, 590 and 660 nm) with a bandwidth of 5 nm at the z plane about 60 μm away from the surface of meta-axicons. Note that the efficiency of the meta-axicon is dependent on wavelength. The efficiency was measured and is shown in Supplementary Fig. S8. The FWHMJ0 and FWHMJ1 for each wavelength spanning 470–680 nm are shown in Supplementary Fig. S9. Figure 4 explicitly indicates that the intensity profile for different wavelengths vary weakly, confirming wavelength-independent behavior. It is notable that for these measurements the distance between the meta-axicon and objective lens was kept unchanged. We also repeated the measurements using a supercontinuum laser of bandwidth 200 nm centered at 575 nm (see Supplementary Fig. S10 for its spectrum). The intensity profiles (Figure 4e and 4j) for both J0 and J1 remarkably changed weakly. It is important to note that in order to generate high NA and wavelength-independent Bessel beams, the Nyquist sampling theorem and wavelength-independent phase gradient conditions both need to be satisfied. According to the Nyquist sampling theorem, one needs to sample the phase profile given by Equation (7) in the spatial domain with a rate that is at least twice the highest transverse spatial frequency. This requires the size of the unit cell to be equal to or smaller than  , which cannot be satisfied by conventional diffractive elements. For example, spatial light modulators usually have ~6 μm pixel sizes46 and photo-aligned liquid crystal devices are usually limited to a phase gradient of ~π/μm47, corresponding to a maximum achievable NA of about 0.03 and 0.26 in the visible region, respectively. It is also important to note that the phase profile of metasurfaces can also be designed by varying the geometrical sizes (length, width or diameter and so on) of the nanostructures, pixel by pixel7, 9. However, these metasurfaces, not designed by the Pancharatnam–Berry phase, are accompanied by strong amplitude differences between each pixel at wavelengths away from the design wavelength. This becomes more significant within the absorption region of the constituent materials used. In addition, the unwanted amplitude difference between each pixel can result in the deflection of light to multiple angles48, changing the profile of the Bessel beams. Utilizing the Pancharatnam–Berry phase approach minimizes the relative amplitude difference between each nano-fin for all wavelengths in the case of circularly polarized illumination, as each nano-fin is identical, and consequently, has the same size. We experimentally demonstrate this concept by measuring meta-axicons consisting of silicon nano-fins from the near-infrared to the visible spectrum, where silicon becomes intrinsically lossy (Supplementary Fig. S11). It is clearly observed that the sizes of the Bessel beam remain constant over the wavelength range of 532–800 nm.
, which cannot be satisfied by conventional diffractive elements. For example, spatial light modulators usually have ~6 μm pixel sizes46 and photo-aligned liquid crystal devices are usually limited to a phase gradient of ~π/μm47, corresponding to a maximum achievable NA of about 0.03 and 0.26 in the visible region, respectively. It is also important to note that the phase profile of metasurfaces can also be designed by varying the geometrical sizes (length, width or diameter and so on) of the nanostructures, pixel by pixel7, 9. However, these metasurfaces, not designed by the Pancharatnam–Berry phase, are accompanied by strong amplitude differences between each pixel at wavelengths away from the design wavelength. This becomes more significant within the absorption region of the constituent materials used. In addition, the unwanted amplitude difference between each pixel can result in the deflection of light to multiple angles48, changing the profile of the Bessel beams. Utilizing the Pancharatnam–Berry phase approach minimizes the relative amplitude difference between each nano-fin for all wavelengths in the case of circularly polarized illumination, as each nano-fin is identical, and consequently, has the same size. We experimentally demonstrate this concept by measuring meta-axicons consisting of silicon nano-fins from the near-infrared to the visible spectrum, where silicon becomes intrinsically lossy (Supplementary Fig. S11). It is clearly observed that the sizes of the Bessel beam remain constant over the wavelength range of 532–800 nm.
Meta-axicons with wavelength-independent intensity profile. Two meta-axicons for J0 (top row) and J1 (bottom row) Bessel beams with NA=0.7 designed at the wavelength λ=532 nm were measured. (a–d, f–i) Measured intensity profiles at wavelengths λ=480, 530, 590 and 660 nm, respectively. Intensity profiles are false colored for ease of visualization. (e, j) J0 (e) and J1 (j) intensity profiles measured using a tunable laser with center wavelength of 575 nm and a bandwidth of 200 nm. Besides changing the exposure time of the camera to avoid saturation, these images were taken without adjusting any other optical component, including the distance between the meta-axicon and objective, which were unchanged throughout the entire measurements. Scale bar=500 nm.
Conclusions
In summary, as a superior alternative to using conventional prism axicons or an objective paired with an annular aperture, we demonstrate high NA meta-axicons capable of generating Bessel beams of different orders in a single device in a much more efficient and compact way. The FWHM of J0 and J1 Bessel beams are shown to be as small as ~160 and 130 nm at the design wavelength λ=405 nm. This size is maintained for an exceptionally large distance of 150λ (depth of focus). Their polarization is space-variant due to high NA. By tailoring the phase profile of the meta-axicons, the FWHMs of generated Bessel beams are made independent of the wavelength of incident light. These meta-axicons can be mass-produced with large diameter using today’s industrial manufacturing (deep ultraviolet steppers). These properties show great promise in potential applications ranging from laser lithography and manipulation to imaging.
References
Durnin J, Miceli JJ, Eberly JH . Diffraction-free beams. Phy Rev Lett 1987; 58: 1499–1501.
Bouchal Z, Wagner J, Chlup M . Self-reconstruction of a distorted nondiffracting beam. Opt Commun 1998; 151: 207–211.
Chen J, Ng J, Lin ZF, Chan CT . Optical pulling force. Nat Photon 2011; 5: 531–534.
Dogariu A, Sukhov S, Jose Sáenz J . Optically induced 'negative forces’. Nat Photon 2013; 7: 24–27.
Brzobohatý O, Čižmár T, Zemánek P . High quality quasi-Bessel beam generated by round-tip axicon. Opt Express 2008; 16: 12688–12700.
Planchon TA, Gao L, Milkie DE, Davidson MW, Galbraith JA et al. Rapid three-dimensional isotropic imaging of living cells using Bessel beam plane illumination. Nat Methods 2011; 8: 417–423.
Sun SL, Yang K-Y, Wang C-M, Juan T-K, Chen WT et al. High-efficiency broadband anomalous reflection by gradient meta-surfaces. Nano Lett 2012; 12: 6223–6229.
Arbabi A, Horie Y, Bagheri M, Faraon A . Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat Nanotechnol 2015; 10: 937–943.
Yu NF, Genevet P, Kats MA, Aieta F, Tetienne J-P et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 2011; 334: 333–337.
Huang LL, Chen XZ, Bai BF, Tan QF, Jin GF et al. Helicity dependent directional surface plasmon polariton excitation using a metasurface with interfacial phase discontinuity. Light Sci Appl 2013; 2: e70.
Sun SL, He Q, Xiao SY, Xu Q, Li X et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat Mater 2012; 11: 426–431.
Sun WJ, He Q, Sun SL, Zhou L . High-efficiency surface plasmon meta-couplers: concept and microwave-regime realizations. Light Sci Appl 2016; 5: e16003.
Chen XZ, Huang LL, Mühlenbernd H, Li GX, Bai BF et al. Dual-polarity plasmonic metalens for visible light. Nat Commun 2012; 3: 1198.
Arbabi A, Horie Y, Ball AJ, Bagheri M, Faraon A . Subwavelength-thick lenses with high numerical apertures and large efficiency based on high-contrast transmitarrays. Nat Commun 2015; 6: 7069.
Khorasaninejad M, Chen WT, Devlin RC, Oh J, Zhu AY et al. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016; 352: 1190–1194.
Khorasaninejad M, Chen WT, Zhu AY, Oh J, Devlin RC et al. Multispectral chiral imaging with a metalens. Nano Lett 2016; 16: 4595–4600.
Khorasaninejad M, Chen WT, Oh J, Capasso F . Super-dispersive off-axis meta-lenses for compact high resolution spectroscopy. Nano Lett 2016; 16: 3732–3737.
Huang LL, Chen XZ, Mühlenbernd H, Zhang H, Chen SM et al. Three-dimensional optical holography using a plasmonic metasurface. Nat Commun 2013; 4: 2808.
Huang YW, Chen WT, Tsai WY, Wu PC, Wang CM et al. Aluminum plasmonic multicolor meta-hologram. Nano Lett 2015; 15: 3122–3127.
Zheng GX, Mühlenbernd H, Kenney M, Li GX, Zentgraf T et al. Metasurface holograms reaching 80% efficiency. Nat Nanotechnol 2015; 10: 308–312.
Ye WM, Zeuner F, Li X, Reineke B, He S et al. Spin and wavelength multiplexed nonlinear metasurface holography. Nat Commun 2016; 7: 11930.
Wang Q, Rogers ETF, Gholipour B, Wang C-M, Yuan GH et al. Optically reconfigurable metasurfaces and photonic devices based on phase change materials. Nat Photon. 2016; 10: 60–65.
Ou J-Y, Plum E, Zhang JF, Zheludev NI . An electromechanically reconfigurable plasmonic metamaterial operating in the near-infrared. Nat Nanotechnol 2013; 8: 252–255.
Karimi E, Schulz SA, De Leon I, Qassim H, Upham J et al. Generating optical orbital angular momentum at visible wavelengths using a plasmonic metasurface. Light Sci Appl 2014; 3: e167.
Chen WT, Török P, Foreman MR, Liao CY, Tsai W-Y et al. Integrated plasmonic metasurfaces for spectropolarimetry. Nanotechnology 2016; 27: 224002.
Khorasaninejad M, Crozier KB . Silicon nanofin grating as a miniature chirality-distinguishing beam-splitter. Nat Commun 2014; 5: 5386.
Lin DM, Fan PY, Hasman E, Brongersma ML . Dielectric gradient metasurface optical elements. Science 2014; 345: 298–302.
Hess O, Pendry JB, Maier SA, Oulton RF, Hamm JM et al. Active nanoplasmonic metamaterials. Nat Mater 2012; 11: 573–584.
Aieta F, Genevet P, Kats MA, Yu NF, Blanchard R et al. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces. Nano Lett 2012; 12: 4932–4936.
Gao L, Shao L, Chen B-C, Betzig E . 3D live fluorescence imaging of cellular dynamics using Bessel beam plane illumination microscopy. Nat Protoc 2014; 9: 1083–1101.
Fahrbach FO, Simon P, Rohrbach A . Microscopy with self-reconstructing beams. Nat Photon. 2010; 4: 780–785.
Brzobohatý O, Karásek V, Šiler M, Chvátal L, Čižmár T et al. Experimental demonstration of optical transport, sorting and self-arrangement using a 'tractor beam’. Nat Photon. 2013; 7: 123–127.
Garcés-Chávez V, McGloin D, Melville H, Sibbett W, Dholakia K . Simultaneous micromanipulation in multiple planes using a self-reconstructing light beam. Nature 2002; 419: 145–147.
Novitsky A, Qiu C-W, Wang HF . Single gradientless light beam drags particles as tractor beams. Phys Rev Lett 2011; 107: 203601.
Yalizay B, Ersoy T, Soylu B, Akturk S . Fabrication of nanometer-size structures in metal thin films using femtosecond laser Bessel beams. Appl Phys Lett 2012; 100: 031104.
Tseng ML, Wu PC, Sun S, Chang CM, Chen WT et al. Fabrication of multilayer metamaterials by femtosecond laser-induced forward-transfer technique. Laser Photon Rev 2012; 6: 702–707.
Berry MV . The adiabatic phase and Pancharatnam's phase for polarized light. J Mod Opt 1987; 34: 1401–1407.
Gori F . Measuring Stokes parameters by means of a polarization grating. Opt Lett 1999; 24: 584–586.
Luo WJ, Xiao SY, He Q, Sun SL, Zhou L . Photonic spin Hall effect with nearly 100% efficiency. Adv Opt Mater 2015; 3: 1102–1108.
Huang LL, Chen XZ, Mühlenbernd H, Li GX, Bai BF et al. Dispersionless phase discontinuities for controlling light propagation. Nano Lett 2012; 12: 5750–5755.
Devlin RC, Khorasaninejad M, Chen WT, Oh J, Capasso F . Broadband high-efficiency dielectric metasurfaces for the visible spectrum. Proc Natl Acad Sci USA 2016; 113: 10473–10478.
Lalanne P, Astilean S, Chavel P, Cambril E, Launois H . Blazed binary subwavelength gratings with efficiencies larger than those of conventional échelette gratings. Opt Lett 1998; 23: 1081–1083.
Bomzon Z, Gu M, Shamir J . Angular momentum and geometrical phases in tight-focused circularly polarized plane waves. Appl Phys Lett 2006; 89: 241104.
Lalithambigai K, Suresh P, Ravi V, Prabakaran K, Jaroszewicz Z et al. Generation of sub wavelength super-long dark channel using high NA lens axicon. Opt Lett 2012; 37: 999–1001.
Novitsky AV, Novitsky DV . Negative propagation of vector Bessel beams. J Opt Soc Am A Opt Image Sci Vis 2007; 24: 2844–2849.
Leach J, Gibson GM, Padgett MJ, Esposito E, McConnell G et al. Generation of achromatic Bessel beams using a compensated spatial light modulator. Opt Express 2006; 14: 5581–5587.
Escuti MJ, Kim J, Kudenov MW . Controlling light with geometric-phase holograms. Opt Photon News 2016; 27: 22–29.
Song L, Lessard RA, Galarneau P . Diffraction efficiency of a thin amplitude-phase holographic grating: a convolution approach. J Mod Opt 1990; 37: 1319–1328.
Acknowledgements
This work was supported in part by the Air Force Office of Scientific Research (MURI, grant# FA9550-14-1-0389), Charles Stark Draper Laboratory, Inc. (SC001-0000000959) and Thorlabs Inc. WTC acknowledges postdoctoral fellowship support from the Ministry of Science and Technology, Taiwan (104-2917-I-564-058). RCD is supported by a Charles Stark Draper Fellowship. AYZ thanks Harvard SEAS and A*STAR Singapore under the National Science Scholarship scheme. This work was performed in part at the Center for Nanoscale Systems (CNS), a member of the National Nanotechnology Coordinated Infrastructure (NNCI), which is supported by the National Science Foundation under NSF award no. 1541959. CNS is a part of Harvard University. We thank E. Hu for the supercontinuum laser (NKT ‘SuperK’).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications’ website.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Chen, W., Khorasaninejad, M., Zhu, A. et al. Generation of wavelength-independent subwavelength Bessel beams using metasurfaces. Light Sci Appl 6, e16259 (2017). https://doi.org/10.1038/lsa.2016.259
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2016.259
Keywords
This article is cited by
-
Non-interleaved chiral metasurfaces and neural networks enhance the spatial resolution of polarimetry
Light: Science & Applications (2024)
-
Bessel light beam for a surgical laser focusing telescope—a novel approach
Lasers in Medical Science (2024)
-
Spin-orbit Rabi oscillations in optically synthesized magnetic fields
Light: Science & Applications (2023)
-
Silicon photonic Bessel–Gaussian beam generation unlocks new possibilities for long-range sensing
Light: Science & Applications (2023)
-
On-chip generation of Bessel–Gaussian beam via concentrically distributed grating arrays for long-range sensing
Light: Science & Applications (2023)