Abstract
Optical filters are essential in a wide range of applications, including optical communications, electronics, lighting, optical sensors and photography. This article presents recent work which indicates that optical filters can be created from specialized nanoparticle suspensions. Specifically, this article describes a theoretical optimization process for designing nanofluid-based filters for hybrid solar photovoltaic/thermal (PV/T) applications. This particular application is suitable because nanofluids can be utilized as both volumetric solar absorbers and flowing heat transfer mediums. The nanofluid filters described in this work compare favorably with conventional optical filters for five photovoltaic (PV) cell alternatives: InGaP, CdTe, InGaAs, Si, and Ge. This study demonstrates that nanofluids make efficient, compact and potentially low-cost, spectrally selective optical filters.
Similar content being viewed by others
List of symbols
- A :
-
Geometric parameter
- a o :
-
Bohr radius (cm)
- D :
-
Diameter (nm)
- E :
-
Spectral irradiance (W m−2µm−1)
- f v :
-
Volume fraction
- n :
-
Charge carrier density (cm−3)
- T :
-
Transmittance
- k :
-
Complex refractive index component
- I :
-
Radiant flux (W m−2)
- L :
-
Length (mm)
- Q :
-
Optical efficiency
- V f :
-
Fermi velocity (m s−1)
Subscripts
- c :
-
Critical density
- e :
-
Electron
- ext :
-
Extinction
- i :
-
ith particle
- p :
-
Plasmon
- bulk :
-
Bulk material property
Greek
- α :
-
Absorbance
- ε o :
-
Permittivity of free space (m−3 kg−1 s4 A2)
- ε :
-
Complex dielectric constant (F m−1 or kg mm mV−2 s−2)
- λ :
-
Wavelength (µm)
- σ :
-
Extinction coefficient (m−1)
- ω :
-
Frequency (s−1)
- τ :
-
Relaxation time (s)
- γ :
-
Relaxation frequency (s−1)
- Γ:
-
Damping constant
- η :
-
Filter efficiency
Introduction
Optical filters are traditionally made of thin films or solid materials. These filters have been designed for a myriad of applications including optical communications, optical sensors, electronics, lighting, photography and energy harvesting. With recent advances in nanofabrication and thin film manufacturing techniques, optical filters have seen a step-change in the number of available production methods and materials. Techniques which provide control on the nanoscale have been successfully deployed to achieve finely tuned spectral properties of thin films.1,2 However, fluid-based filters remain relatively underdeveloped.
Hybrid photovoltaic/thermal (PV/T) solar collectors can theoretically be designed to operate at near 80% in combined efficiency.3 This represents almost double the efficiency of the best photovoltaic (PV) only systems, for which the record test efficiency for PV cells in 2012 was 43.5%±2.6% (multijunction cells).4 If designed well, PV/T systems can also provide significant financial savings for residential and industrial applications where demands for both electrical and thermal energy are presented.5,6 Several PV/T concepts have been proposed.3 Most commonly PV/T systems put the working fluid directly in contact with the PV system, thereby removing excess heat. This type of design necessitates a compromise between the drop in efficiency with temperature for PV cells and the value of higher output temperatures from the thermal system. While straightforward, an integrated system forces operation temperatures to be moderate, in the range of 30–100 °C.4 In concentrating PV/T (or CPV/T) solar systems, irradiance on the receiver is high causing the compromise in performance to be even more pronounced.
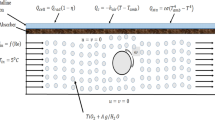
This article suggests that nanofluids—nanoparticles suspended in conventional base fluids—provide one possible solution to the challenges discussed above. Several studies have investigated the capacity for nanoparticles and nanofluids to achieve tunable optical properties.7,8,9,10,11 Additionally, previous work of the co-authors12,13,14,15,16,17,18,19,20 has shown that nanofluid mixtures can improve the performance of solar thermal systems. Other studies have shown that pure fluids (water and organic liquids) can be applied to solar systems as optical filters.21,22 However, the potential for nanofluids to be used as selective absorbing fluids has not been previously explored. Therefore, this study demonstrates that alternative liquid nanofluid optical filters can achieve the same level of control as conventional optical filters. The advantage of using nanofluids is that they can easily be pumped in and out of a system or controlled by magnetic/electric fields, making them ideal for applications where dynamic optical switching is desired. For solar energy harvesting applications, this is especially advantageous because a nanofluid-based filter can also be used as the heat transfer and thermal storage medium. Thus, with a nanofluid filter, it is possible to de-couple the PV and thermal systems so that each can operate at optimum temperature. The general schematic for this type of PV/T system is shown in Figure 1.
Methods and assumptions
The aim of this study was to develop optimized nanofluid-based filters to match with several PV cell options: InGaP, CdTe, InGaAs, Si and Ge. These PV cells were chosen to demonstrate the versatility of nanofluid filters over the entire solar spectrum. The following sections describe the process used in this study to achieve optimized filters for these cells.
Particle material selection
To obtain nanofluids with optical properties corresponding to the spectral response of these cells, the bulk materials were chosen carefully. As a starting point for modeling, this study reviewed optical property data for many materials from the handbook edited by Palik.23 Most pure materials have either very broad absorption or absorption outside solar wavelengths. As such, the list of suitable materials is relatively short, including: doped semiconductors, metals and core/shell composite nanoparticles. Doped semiconductors present a feasible nanoparticle material choice because they absorb and transmit light in a similar range as PV cells. Due to their strong plasmon resonance over a short spectral range, some metals are well suited to this application. Noble metals are a particularly attractive subset because they are resistant to oxidation and corrosion. Lastly, core/shell nanoparticles are attractive as well because the shell to core radius ratio can be controlled to tune optical absorption.24,25,26,27,28 Likewise, they can have more pronounced absorption peaks than pure metals and use considerably less metal material, which represents a potential cost benefit over pure metal nanoparticles. Thus, core/shell nanoparticles with noble metal shells were chosen as a focus of this study.
To achieve volumetric absorption—where light is absorbed over a finite light path inside the fluid—the particle volume fraction was assumed to be in the range of 0%–0.1% by volume. That is, for a relatively thick volumetric absorber (100 mm), only a low volume fraction of particles (i.e., less than 1×10−5%) was needed to absorb the wavelengths of interest. For a thin filter (0.1 mm), volume fractions near 0.1% by volume were required for sufficient absorption.
Nanoparticle sizes in the range of 20–50 nm in diameter were used in this study. This size constraint assured that particles followed the flow, did not foul and/or abrade pumps and plumbing, and were available ‘off-the-shelf’.29,30,31 Table 1 summarizes the design parameters used in this study. It should also be noted that nanofluids should be stabilized for long-term operation in real-world applications,32,33,34 but this is outside the scope of this work.
Calculation of nanofluid optical properties
Nanofluid optical properties were calculated in this study through the following procedure: (i) determination of bulk material properties; (ii) modification of bulk properties based on particle characteristics; (iii) calculation of particle extinction efficiencies; (iv) particle mixture selection; and (v) volume fraction optimization. Note: Steps iv and v were iterative and were done separately for each type of PV cell.
Determination of bulk material properties
As a first step, data of the bulk materials were obtained for the materials used in this study from ref. 23. For the optical filters designed in this study, these properties were known over the majority of the solar spectrum containing substantial energy (i.e., 0.25–2.5 µm). The pure fluid choices for this study were based on the results of Kaluza et al.21 and Chendo et al.22 These studies indicated that water, heat transfer oils (such as Therminol VP-1) and Brayco 888F were potential options for spectrally selective fluids over the solar wavelengths. If bulk material property data were not available, as was the case for proprietary heat transfer oils, a ultraviolet–infrared spectrophotometer was required to measure them. Thus, Therminol VP-1 oil optical data were measured by the co-authors for this study.
Modification of bulk properties based on particle characteristics
The next step was to modify the bulk properties based on particle size, addition of dopants, and whether or not the materials were incorporated into a core/shell nanoparticle. The Drude–Lorentz model was the starting point for each of these modifications. The model assumes that electrons are harmonically bound to the nucleus.
Size effect modification
When the nanoparticle diameter nears the mean free path of the bulk material, boundary effects can become important. This effect has been demonstrated numerically,35 and confirmed experimentally for metallic nanoparticles.36 To account for this, the bulk properties were modified through the damping coefficient in the Drude–Lorentz model. As such, the Drude–Lorentz model can be transformed into the following expression:37,38,39

where ε(ω)exp is the bulk complex dielectric constant (from handbook data), ωp is the bulk plasmon frequency, ω is the variable electromagnetic wave frequency and γbulk is the relaxation frequency of bulk metal. The small particle modification term, γ(leff), is defined as the following:40,41

In this equation, τo is the bulk metal free electron scattering time, A is a geometric parameter assumed to be 1,35 Vf is the Fermi velocity (where an experimental values on the order of Vf≈106 m s−1 are used42), and D is the particle diameter which is used as the effective mean free path. For example, copper and silver have mean free paths around 50 nm.43 Thus, Equations (1) and (2) are used when the particles are less than or equal to the mean free path. When this is the case, the mean free path is assumed to be restricted to the particle diameter.
Addition of dopants
Semiconductor materials are viable for use in a nanofluid band-pass filter since they have complementary optical properties to PV cells. To calculate the optical properties, the effect of added dopants must be included. For high absorption in the selected regions, significant dopant concentrations are necessary. With heavy doping, it is possible to exceed the Mott critical density, nc. The parameter ranges from ∼6×1013 cm−3 for InSb to ∼3×1018 cm−3 for Si and were calculated by the following:44

where the Bohr orbit radius is denoted as ao. Thus, Equations (1) and (2) also apply to semiconductor nanoparticles. In this case, however, the bulk plasmon frequency, ωp, was modified based on the carrier density:45

where ne is the electron density, e is the electronic charge, me is the effective electron mass and εo is the permittivity of free space. Thus, Equation (4) was used in Equation (1) to determine the optical properties of semiconductor nanoparticles.
Core/shell nanoparticles
Metallic shell/dielectric (silica) core particles were chosen because their plasmon resonance is very pronounced. That is, under specific wavelength, polarization and incident angle conditions, free electrons (plasma) at the surface of the nanoparticle strongly absorb incident photons. Therefore, a narrow band of wavelengths is converted into plasmon waves which spread across the surface. The wavelengths at which this occurs are determined by the particle’s size, shape, shell thickness and the bulk optical properties of the materials involved.46 As was shown in a seminal study by Oldenburg et al.,9 controlling the ratio of the shell radius to the core radius can allow for strong plasmon resonance tuning.
The modeling assumption used for core/shell nanoparticles was the quasi-static approximation. This assumption is valid if particles are much smaller than the wavelength of light and if the incident light does not vary over the particle diameter. Both of these assumptions were applicable to the nanofluids of this study. To find the properties of an individual nanoparticle, the approach of Lv et al.39 was used.
Calculation of particle extinction efficiencies
For the design space of this study, the Rayleigh scattering approximation was valid. In this regime, absorption, scattering and extinction efficiencies from the optical properties are calculated using the approach of Bohren and Huffman.47 Figure 2 plots the spectral extinction efficiency for selecting particle options calculated using the above approach. Note: extinction efficiency is a non-dimensional parameter which is defined as the effective light extinction cross-section divided by the geometric cross-section. It can be seen that particle options are available over ultraviolet to near infrared wavelengths (0.25–2 µm).
Particle mixture selection
Depending on the PV cell, various nanoparticles were selected. Since PV designs can be quite variable, this study optimizes based on an ‘ideal’ approximations of PV material response curves. For example, the ‘ideal’ filter for a silicon PV cell was assumed to absorb wavelengths shorter than 0.75 µm and those longer than 1.125 µm. Table 2 shows the assumptions made for the various PV cells used in this study.
The base fluid will also absorb light. Water and Therminol VP-1 are effectively transparent for wavelengths shorter than 1.5 µm, but highly absorbing beyond 1.5 µm. To keep the resulting nanofluid suspensions and optimization somewhat straightforward, only two- and three-particle liquid filters were modeled in this study. In general, any number of particles could be chosen to meet the specifications of the application.
Volume fraction optimization
The volume fraction, fv, of the each type of nanoparticle was a key parameter for optimization in this study. This was determined by calculating the extinction coefficient from the following equation:47

where i represents the ith particle and Qext represents the extinction efficiency of the particle. It should be noted that this is only valid for small particle, low volume fraction nanofluids, i.e., the constraints of Table 1. Since the base fluid can contribute to the extinction of light through a nanofluid, this study assumes that the total nanofluid extinction coefficient is a simple addition of the base fluid extinction coefficient and that of the particles, defined as the following:

Note: This approximation has been shown to be experimentally valid.18 By varying the thickness of the base fluids, the most suitable base fluid configuration for each type of PV cell was determined. Beer’s law provides a good first-order spectral approximation of the amount of light transmitted/absorbed by these fluid filters:47

where T is the transmittance, α is absorbance, I is the transmitted irradiation, Io is the incident irradiation and L is the length of the light path in the filter. This simple calculation does not separate the effect of scattering. For a nanofluid filter, scattering (i.e., lost solar energy) should be much less than 10% of total extinction (note: small particles scatter much less than large particles). In this study, low scattering was assured by putting a constraint of 0.1 for the ratio of scattering efficiency to extinction efficiency.
To determine the efficiency of a nanofluid as a band-pass filter, this study used the following partitioned integral:

where Eλ is the amount of solar irradiance per unit wavelength—data for Eλ can be obtained from Gueymard.48 A perfectly transparent (T=1) filter between the short and long edges shown in Table 2 which is also perfectly absorbing (T=0) outside of that range, will achieve an efficiency of 1. Thus, Equation (8) is the objective function for filter optimization. This study uses a simple Monte Carlo approach to randomly generate volume fraction combinations which can be sorted by η to find the optimum filter.
Results and discussion
The results of this optimization process are shown in Figures 3–7. Each figure corresponds to a different PV cell. The y-axes depict absorbance (ranging from 0 to 1) as a function of wavelength (0.25–2.5 µm) on the x-axes. In the figures, the study results are compared to ideal, pure fluid, and conventional filters using data obtained from Schott.49 Thus, each curve represents a fluid that can fit into Figure 1—where heat can be pumped to a thermal system. The figures show that in most cases the base fluids are highly absorbing at long wavelengths. Thus, large base fluid absorbance can be seen in the figures at wavelengths >1.5 µm. Since pure water is essentially a short-pass filter, H2O makes a relatively good selective absorber for InGaP and CdTe. A similar reasoning shows that Brayco 888F gives the best selectivity for an InGaAs cell. For a Si cell, conventional Valvoline motor oil (low viscosity), is the most efficient pure fluid as it gives a reasonable spectral match. Since all of the pure fluids tested in this study absorb some of the ideally transmitted spectrum for a Ge cell, a thin layer of Therminol VP-1 was found to be the best pure fluid for a Ge cell.
The highest solar weighted efficiency achieved in this study, η, is found to be 76.1% for CdTe using a conventional filter with H2O. As compared with conventional filters, two- and three-particle nanofluid filters are generally not as good in terms of solar weighted efficiency, η. The exception is the Ge cell where the conventional filter has an η=63.9%, but a nanofluid filter can achieve η=67.1%. The optimized nanofluid filter is thinner (9–20 mm) as compared to pure fluids and conventional filters—shown in Table 3. This indicates a more compact CPV/T design may be possible with nanofluid-based optical filters. Table 3 summarizes the particle volume fractions used to achieve each filter and the associated filter efficiency values calculated from the objective function of Equation (8). It should be pointed out that in these optimized designs, the highest particle volume fraction, fv, is <1×10−4 (i.e., <0.01% by volume). Importantly, this means that very few particles are needed to create these filters. Overall, these results indicate that nanofluid optical filters can potentially be employed in any number of CPV/T systems.
Conclusions
This study presented innovative designs of nanofluid-based optical filters for PV/T systems. Nanofluid-based filters provide superior solar-weighted efficiency to pure fluids and comparable efficiency to conventional optical filters over the solar wavelengths—ultraviolet to near infrared. In addition, the resulting nanofluid filters are considerably more compact than a pure fluid filter or a conventional filter surrounded by a pure fluid. Another advantage of liquid filters is that they can potentially be controlled—dynamically—with pumps, magnetic/electric fields and temperature changes. The optimization results of this study reveal that, at most, a volume fraction of 0.0011% is required to achieve optimum filters for CPV/T applications. A big advantage of core/shell nanoparticles is that only a small fraction of each particle is metal, while the majority is silica. This results in an inexpensive nanofluid since little metal material is required to create highly absorbing particles. This indicates excellent potential for very low-cost liquid filters with comparable performance to conventional filters.
Future work
The goal of this study was to demonstrate the versatility of novel nanofluid collectors and several potential avenues were identified for future work. The effect of stabilization agents (surface chemistry modification) and linker agents (such as silanes) which are necessary in the fabrication process is unknown. The addition of many more particles to achieve more complex filtration could help to achieve a better filter. Experimental studies are needed to measure filter performance. Lastly, for real applications, an economic optimization based on the price of fabrication and the relative value of electricity vs. heat (based on location) is needed.
References
Zaitsu S, Jitsuno T, Nakatsuka M, Yamanaka T, Motokoshi S . Optical thin films consisting of nanoscale laminated layers. Appl Phys Lett 2002; 80: 2442–2444.
Imenes AG, Mills DR . Spectral beam splitting technology for increased conversion efficiency in solar concentrating systems: a review. Sol Energy Mater Sol Cells 2004; 84: 19–69.
Chow TT . A review on photovoltaic/thermal hybrid solar technology. Appl Energy 2010; 87: 365–379.
Green MA, Emery K, Hishikawa Y, Warta W, Dunlop ED . Solar cell efficiency tables (version 39). Prog Photovoltaics: Res Appl 2012; 20: 12–20.
Tripanagnostopoulos Y, Souliotis M, Battisti R, Corrado A . Energy, cost and LCA results of PV and hybrid PV/T solar systems. Prog Photovoltaics: Res Appl 2005; 13: 235–250.
Beccali M, Finocchiaro P, Nocke B . Energy and economic assessment of desiccant cooling systems coupled with single glazed air and hybrid PV/thermal solar collectors for applications in hot and humid climate. Sol Energy 2009; 83: 1828–1846.
Mock JJ, Barbic M, Smith DD, Schultz DA, Schultz S . Shape effects in plasmon resonance of individual colloidal silver nanoparticles. Chem Phys 2002; 116: 6755.
Liz-Marza LM . Tailoring surface plasmons through the morphology and assembly of metal nanoparticles. Langmuir 2006; 22: 32–41.
Oldenburg SJ, Averitt RD, Westcott SL, Halas NJ . Nanoengineering of optical resonances. Chem Phys Lett 1998; 288: 243–247.
Mishra A, Tripathy P, Ram S, Fecht HJ . Optical properties in nanofluids of gold nanoparticles in poly(vinylpyrrolidone). J Nanosci Nanotechnol 2009; 9: 4342–4347.
Mishra A, Ram S, Ghosh G . Dynamic light scattering and optical absorption in biological nanofluids of gold nanoparticles in poly(vinyl pyrrolidone) molecules. J Phys Chem C 2009; 113: 6976–6982.
Otanicar TP, Phelan PE, Golden JS . Optical properties of liquids for direct absorption solar thermal energy systems. Sol Energy 2009; 83: 969–977.
Otanicar TP, Phelan PE, Prasher RS, Rosengarten G, Taylor RA . Nanofluid-based direct absorption solar collector. J Renew Sustain Energy 2010; 2: 033102.
Otanicar TP, Chowdhury I, Prasher R, Phelan PE . Band-gap tuned direct absorption for a hybrid concentrating solar photovoltaic/thermal system. J Sol Energy Eng 2011; 133: 041014.
Otanicar TP, Phelan PE, Taylor RA, Tyagi H . Spatially varying extinction coefficient for direct absorption solar thermal collector optimization. J Sol Energy Eng 2011; 133: 024501.
Otanicar TP, Phelan PE, Taylor RA . Tuning the extinction coefficient for direct absorption solar thermal collector optimization. ASME Conf Proc 2010; 1: 819–824.
Otanicar TP, Taylor RA, Phelan PE, Prasher RS . Impact of size and scattering mode on the optimal solar absorbing nanofluid. In: Proceedings of the ASME 2009 3rd International Conference of Energy Sustainability; 19–23 July 2009; San Francisco, CAUSA. ASME: New York, USA, 2009, Vol. 1, pp 791–796.
Taylor RA, Phelan PE, Otanicar TP, Adrian R, Prasher R . Nanofluid optical property characterization: towards efficient direct absorption solar collectors. Nanoscale Res Lett 2011; 6: 225.
Taylor RA, Phelan PE, Otanicar TP, Walker CA, Nguyen M et al. Applicability of nanofluids in high flux solar collectors. J Renew Sustain Energy 2011; 3: 023104.
Taylor RA, Phelan PE, Otanicar T, Adrian RJ, Prasher RS . Vapor generation in a nanoparticle liquid suspension using a focused, continuous laser beam. Appl Phys Lett 2009; 95: 161907.
Kaluza J, Funken KH, Groer U, Neumann A, Riffelmann KJ . Properties of an optical fluid filter: Theoretical evaluations and measurement results. J Phys IV 1999; 9: Pr3-655–Pr3-660.
Chendo MA, Jacobson MR, Osborn DE . Liquid and thin-film filters for hybrid solar energy conversion systems. Sol Wind Technol 1987; 4: 131–138.
Palik ED . Handbook of optical constants of solids, five-volume set. New York: Academic Press, 1997: 999.
Zou S, Janel N, Schatz GC . Silver nanoparticle array structures that produce remarkably narrow plasmon lineshapes. J Chem Phys 2004; 120: 10871–10875.
Garcia G, Buonsanti R, Runnerstrom EL, Mendelsberg RJ, Llordes A et al. Dynamically modulating the surface plasmon resonance of doped semiconductor nanocrystals. Nano Lett 2011; 11: 4415–4420.
Zou S, Schatz GC, Introduction I . Narrow plasmonic/photonic extinction and scattering line shapes for one and two dimensional silver nanoparticle arrays. J Chem Phys 2004; 121: 12606–12612.
Halas NJ, Lal S, Chang WS, Link S, Nordlander P . Plasmons in strongly coupled metallic nanostructures. Chem Rev 2011; 111: 3913–3961.
Palombo N, Park K . Investigation of dynamic near-field radiation between quantum dots and plasmonic nanoparticles for effective tailoring of the solar spectrum. ASME Conf Proc 2011; 4: 1715–1719.
NanoComposix. nanoComposix Products. San Diego, CA: NanoComposix, 2012. Available at http://nanocomposix.com/products (accessed 22 April 2012).
Sigma-Aldrich. Nanopowders. St Louis, MO: Sigma-Aldrich, 2010. Available at http://www.sigmaaldrich.com/materials-science/nanomaterials/nanopowders.html (accessed 17 May 2012)
NanoAmor. Catalog of Nanoscale Particulate Materials. Houston, TX: NanoAmor, 2010. Available: http://www.nanoamor.com/cat/catalog_nanoamor.pdf (accessed 17 May 2012)
Ghadimi A, Saidur R, Metselaar HS . A review of nanofluid stability properties and characterization in stationary conditions. Int J Heat Mass Transfer 2011; 54: 4051–4068.
Tavares J, Coulombe S . Dual plasma synthesis and characterization of a stable copper–ethylene glycol nanofluid. Powder Technol 2011; 210: 132–142.
Keblinski P, Eastman JA, Cahill DG . Nanofluids for thermal transport. Mater Today 2005; 8: 36–44.
Kreibig U, Vollmer V . Optical properties of metal clusters. 1st ed. Aachen: Springer, 2010.
Averitt R, Sarkar D, Halas N . Plasmon resonance shifts of Au-coated Au2S nanoshells: insight into multicomponent nanoparticle growth. Phys Rev Lett 1997; 78: 4217–4220.
Neeves AE, Birnboim MH . Composite structures for the enhancement of nonlinear-optical susceptibility. J Opt Soc Am B 1989; 6: 787.
Fox M . Optical properties of solids. 2nd ed. Oxford: Oxford University Press, 2010.
Lv W, Otanicar TP, Phelan PE, Dai L, Taylor RA et al. Surface plasmon resonance shifts of a dispersion of core–shell nanoparticles for efficient solar absorption. In: Proceedings of ASME 3rd 2012 Micro/Nanoscale Heat & Mass Transfer International Conference; Atlanta, GAUSA; 3–6 March 2012. ASME: New York, USA, MNHMT 2012– 75090.
Johnson PB, Christy RW . Optical constants of the Noble metals. Phys Rev B 1972; 6: 4370–4379.
Grady NK, Halas NJ, Nordlander P . Influence of dielectric function properties on the optical response of plasmon resonant metallic nanoparticles. Chem Phys Lett 2004; 399: 167–171.
Kittel C . Introduction to solid state physics. 8th ed. Hoboken, NJ: John Wiley & Sons, 2004.
Berglund CN, Spicer WE . Photoemission studies of copper and silver: theory. Phys Rev 1964; 136: A1030–A1044.
Hugon PL . Pressure-induced Mott transition in doped semiconductors. Phys Lett 1971; 34: 120–121.
Ederth J, Johnsson P, Niklasson GA, Hoel A, Hultåker A et al. Electrical and optical properties of thin films consisting of tin-doped indium oxide nanoparticles. Phys Rev B 2003; 68: 1–10.
Kelly LK, Coronado E, Zhao LL, Schatz GC . The optical properties of metal nanoparticles: the influence of size, shape, and dielectric environment. J Phys Chem B 2003; 107: 668–677.
Bohren CF, Huffman DR . Absorption and scattering of light by small particles. New York: Wiley-VCH, 1998: 544.
Gueymard C . Parameterized transmittance model for direct beam and circumsolar spectral irradiance. Sol Energy 2001; 71: 325–346.
SCHOTT. Optical Filters. Mainz: SCHOTT, 2012. Available at http://www.schott.com/advanced_optics/english/filter/index.html?PHPSESSID=ra0uavqiou413sfj003ublirj4 (accessed 10 March 2012).
Acknowledgements
RAT and GR gratefully acknowledge the support of the Australian Solar Institute and the UNSW ECR funding scheme. TO gratefully acknowledges support from USA NSF grant CBET-1066705.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This work is licensed under the Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Taylor, R., Otanicar, T. & Rosengarten, G. Nanofluid-based optical filter optimization for PV/T systems. Light Sci Appl 1, e34 (2012). https://doi.org/10.1038/lsa.2012.34
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2012.34
Keywords
This article is cited by
-
Multiple Nanoparticles Coupling Strategy for Enhancing Optical Filter Performance of Spectral Splitter Used in Photovoltaic/Thermal System
Journal of Thermal Science (2023)
-
A critical review of concentrating and nanofluid-based hybrid PV/T systems utilizing beam splitting technique: Progress, challenges, and way forward
Environmental Science and Pollution Research (2023)
-
A versatile interferometric technique for probing the thermophysical properties of complex fluids
Light: Science & Applications (2022)
-
Assessment of alumina/water nanofluid in a glazed tube and sheet photovoltaic/thermal system with geothermal cooling
Journal of Thermal Analysis and Calorimetry (2022)
-
Efficiency limits of concentrating spectral-splitting hybrid photovoltaic-thermal (PV-T) solar collectors and systems
Light: Science & Applications (2021)