Abstract
Finding gene interaction models is one of the most important issues in genotype–phenotype association studies. This paper presents a model-free nonparametric statistical interaction analysis known as Parallel Haplotype Configuration Reduction (pHCR). This technique extends the original Multifactor Dimensionality Reduction (MDR) algorithm by using haplotype contribution values (c-values) and a haplotype interaction scheme instead of analyzing interactions among single-nucleotide polymorphisms. The proposed algorithm uses the statistical power of haplotypes to obtain a gene–gene interaction model. pHCR computes a statistical value for each haplotype, which contributes to the phenotype, and then performs haplotype interaction analysis on the basis of the cumulative c-value of each individual haplotype. To address the high computational complexity of pHCR, this paper also presents a scalable parallel computing solution. Nine common two-locus disease models were used to evaluate the algorithm performance under different scenarios. The results from all cases showed that pHCR shows higher power to detect gene–gene interaction in comparison with the results obtained from running MDR on the same data set. We also compared pHCR with FAMHAP, which mainly considers haplotype in the association analysis. For every experiment on the simulated data set, pHCR correctly produced haplotype interactions with much fewer false positives. We also challenged pHCR with a real data set input of β-thalassemia/Hemoglobin E (HbE) disease. The result suggested the interaction between two previously reported quantitative trait loci of the fetal hemoglobin level, which is a major modifying factor, and disease severity of β-thalassemia/HbE disease.
Similar content being viewed by others
Introduction
Genetic association studies have been proven to potentially identify susceptibility genes contributing to several complex diseases. In a classical Mendelian disease model, genetic susceptibility factors directly and independently contribute to disease risks. On the other hand, multiple genetic and environmental factors that are dependent on one another (gene–gene and gene–environment interactions) contributing to the phenotypic outcomes of complex diseases. Therefore, the individual effect of each genetic factor could be marginal in each subject, leading to difficulties in obtaining statistically robust genotype–phenotype correlations. Several recent association studies could not be reproduced, possibly because the underlying epistasis (gene–gene interaction) was not considered in the analysis. Therefore, the search for gene–gene interactions has gained momentum.1, 2, 3
Many statistical analysis techniques have been developed while searching for gene–gene interactions. The Multifactor Dimensionality Reduction (MDR) technique is one of the most popular nonparametric algorithms developed by Ritchie et al.4, 5 and it has been widely applied to many real data sets.6, 7, 8, 9 MDR identifies the possible interactions between multiple genes using the differences between cases and controls of all possible genotype combinations. This algorithm relies neither on statistical parameters nor on the adoption of any genetic model. Given a set of multiple single-nucleotide polymorphism (SNP) loci, MDR searches for interactions among these loci by observing all SNP genotyping combinations of a given group size. MDR determines the total number of individuals for each genotype combination. If there are more affected subjects (cases) than unaffected (controls) individuals, the genotype combination is identified as either ‘high risk’ or ‘low risk,’ respectively. An interaction model is chosen when its SNP genotyping combinations can best classify individuals with the minimum misclassification rate. The algorithm internally validates the best model by using a 10-fold cross-validation technique. Since the introduction of MDR, various aspects of the technique have been studied, and extensions have been made to improve its statistical power.10, 11, 12, 13, 14
It is generally known that by considering haplotypes, the statistical power of the analysis can be increased by including linkage disequilibrium (LD) information of multiple SNPs, which reflects the underlying architecture of ancestral chromosomes. Hence, haplotype analysis has an advantage over that of individual SNPs, from both biological and statistical perspectives.15, 16 From a biological point of view, haplotypes reflect the underlying nonrandom organization of the genome into regions under differing evolutionary constraints. In addition, the functional properties of genes are determined by the linear sequence of DNA on a chromosome. From a statistical point of view, combining multiple SNPs into a larger haplotype unit reduces the analytical dimensions. Moreover, many studies have proven the superiority of using haplotypes over SNPs.17
Becker et al.18 proposed a statistical-based algorithm, known as FAMHAP, that analyzes gene–gene interactions in association studies using haplotypes. Instead of using genotypic information for the analysis, FAMHAP uses the expectation-maximization technique to infer haplotypes from the input genotypes. Inferred haplotypes with high frequencies contribute to high weighting factors known as contribution values (c-values). The χ2 test is conducted on all possible combinations of haplotypes in the search for interactions that associate with disease state. However, the statistical test by FAMHAP does not generate classification models and could lead to too many false-positive results if the distribution is not χ2.
Therefore, we propose a Parallel Haplotype Configuration Reduction (pHCR) framework that adapts the combinatorial calculation of interactions presented in MDR. Instead of constructing multi-locus SNP genotyping combinations, pHCR calculates the c-value of multiregion haplotypes and observes the interactions from these new haplotype units. The c-value reflects the contribution of each haplotype to the underlying disease status. The pHCR algorithm also uses a cross-validation strategy to explore the best multiregion haplotype configuration that can best classify patients into high- or low-risk groups with maximum classification accuracy. To overcome the large number of combinations of haplotype interaction, we created a parallel algorithm that allows the combinational analysis part of pHCR to be executed in parallel on any computer cluster that can support the message-passing interface framework.
Materials and methods
The pHCR algorithm follows the dimensionality reduction step of MDR to explore the underlying multiregion haplotype interaction.4, 5 Unlike MDR in which interactions among different SNP loci are explored, pHCR considers interactions of r different unlinked regions, known as the r-interaction model. By exploring every possible interaction of N unlinked regions, the goal is to identify the interaction that can best classify cases and controls, noting that the term ‘interaction’ indicates the multiregion interaction in which r different unlinked regions (r-interaction model) are selected from the total N unlinked regions that produce the interaction. Therefore, the input to pHCR requires haplotype information, including all possible individual haplotypes. It is worth noting that pHCR can generally accept standard genotyping data as its input when considering allelic combinations instead of genotypic combinations.
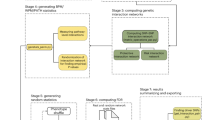
Figure 1 shows the algorithm steps of pHCR that uses the cross-validation framework as a control measurement for the best interaction selection. Therefore, in step 1 of pHCR, case and control subjects are divided into cross-validation groups, for example, 10 groups. During the cross-validation stage, each group takes turns to be the test group, whereas the rest are combined into the training group. In step 2 of pHCR, r different unlinked regions are selected from the total N unlinked regions to produce the interactions. The total number of interactions produced from N unlinked regions of the r-interaction model is then equal to N!/(r!(N−r)!).
In step 3, for each interaction created during step 2, a table of all possible haplotype combinations is created. If input haplotypes are not given and if their frequencies must be inferred from the SNP genotyping data, the uncertainties in haplotype estimation should be taken into account. The c-value concept used in FAMHAP is used to represent the probability of a given haplotype combination contributing to the disease status of a subject. In general, an individual should have two haplotypes. Each haplotype can be considered as a contributor to the disease status of that subject, and the contributions are assumed to be the same. The c-value of each haplotype for a subject should be equal to one-half (0.5), if there is no haplotype ambiguity. However, if haplotype ambiguity exists, the c-value already incorporates the chance that the subject has a given haplotype. Hence, the summation of the c-value of each subject equals 1 (see below).
In step 4 of pHCR, the c-values obtained from case and control subjects are calculated and counted separately according to their haplotype combinations. If the ratio of the accumulated c-value of cases versus controls is greater than a preset threshold, for example, 1 in case the number of cases and controls are equal, then such a haplotype combination is classified as high risk, whereas a c-value ratio below the threshold is classified as low risk. Misclassification errors of the interaction are calculated on the basis of the training group, whereas the test group is used to validate the trained model in each cross-validation step. In step 5, steps 3 and 4 of pHCR are processed repeatedly until every interaction produced in step 2 is investigated. All interaction models are ranked, and the model that has the minimum misclassification error is reported as the best interaction of the cross-validation.
In step 6, the entire process from steps 2 to 5 is repeated until every cross-validation group takes a turn to be a test group. The evidence of a gene–gene interaction is chosen as the best overall model by the interaction that has the highest cross-validation consistency and the lowest average prediction error in the overall cross-validation process. In case two interactions have equal measures, the interaction with the fewer number of regions is chosen to be the best overall model. The significance level of the best overall model is defined by permutation test of the original data set.
A parallelization solution for pHCR was implemented to accommodate a large number of SNPs. The large number of interactions created in step 2 is divided and assigned to each processor when steps 3–5 are analyzed concurrently. However, pre-calculation of all possible interactions could result in high memory complexity, that is, storing all possible interactions on disk. Thus, instead of sending all interactions that will only be partially processed by each processor, pHCR uses our novel algorithm, known as ranked interaction, which locates the proper execution starting point within the list of all possible interactions for each processor. Each processor is responsible for regenerating the actual combinations that are only a small part of the whole interaction set (see Supplementary Information).
Haplotype interaction and contribution value
In this section, the algorithm for computing contribution value (c-value) is presented. The basic idea of c-value is that different haplotype combinations (including haplotype ambiguities) of an individual subject contribute to the disease phenotype. Therefore, c-value represents the probability of a given haplotype combination contributing to an individual's disease status being weighted by the probability of that individual having a given haplotype combination.
Assume that there are N independent genomic regions. We consider haplotypes for each of the N genomic regions both in the population and in each subject. A subject possesses two haplotypes for each genomic region. The two haplotypes can be inferred on the basis of the population haplotype frequencies and the observed genotypes of the subject at the loci within the genomic region. Let  denote the observed genotypes in the lth genomic region of the qth subject. It must be noted that
denote the observed genotypes in the lth genomic region of the qth subject. It must be noted that  is a set of genotypes from more than one locus. Let
is a set of genotypes from more than one locus. Let  denote the population frequency of the ith haplotype in the lth genomic region, and let fl denote a set of population frequencies of all haplotypes in the lth genomic region.
denote the population frequency of the ith haplotype in the lth genomic region, and let fl denote a set of population frequencies of all haplotypes in the lth genomic region.
We consider a haplotype combination (diplotype configuration) for a subject in a genomic region. Let  denote the haplotype combination for the qth subject in the lth genomic region composed of the ith and jth haplotypes (1⩽i⩽j⩽s(l)), where s(l) denotes the number of haplotypes in the lth genomic region. The haplotype combination for a subject q in a genomic region l cannot necessarily be determined from the observed genotypes
denote the haplotype combination for the qth subject in the lth genomic region composed of the ith and jth haplotypes (1⩽i⩽j⩽s(l)), where s(l) denotes the number of haplotypes in the lth genomic region. The haplotype combination for a subject q in a genomic region l cannot necessarily be determined from the observed genotypes  . Rather, more than one haplotype combination is consistent with
. Rather, more than one haplotype combination is consistent with  ; let δ denote the set of the combinations of indexes for all pairs of haplotypes in the lth genomic region consistent with
; let δ denote the set of the combinations of indexes for all pairs of haplotypes in the lth genomic region consistent with 
The probability that the qth subject contains the combination of the ith and jth haplotypes (i⩽j) (diplotype configuration) in the lth genomic region, given the observed genotypes  and population haplotype frequencies (fl), will be
and population haplotype frequencies (fl), will be

for (i, j) ∈ δ, where

We consider gene–gene interactions among r of the N independent genomic regions. There are N!/(r!(N−r)!) different sets of the r genomic regions; let θu denote the indexes of the uth set (u=1, 2,…, N!/(r!(N−r)!)). We only consider the r genomic regions whose indexes are in θu. By drawing each one of the haplotypes from each of the r different genomic regions, we can construct a list of haplotypes with size r. Therefore, let  denote a list of haplotypes with size r, where aj (j=1, 2, , r) represents the jth factor in θu (1⩽aj⩽N)), and
denote a list of haplotypes with size r, where aj (j=1, 2, , r) represents the jth factor in θu (1⩽aj⩽N)), and  denotes the kth haplotype in the lth genomic region (among N genomic regions). The variable bj represents the index of a haplotype in the
denotes the kth haplotype in the lth genomic region (among N genomic regions). The variable bj represents the index of a haplotype in the  genomic region (1⩽bj⩽(s(aj)), where s(aj) is the number of possible haplotypes in the
genomic region (1⩽bj⩽(s(aj)), where s(aj) is the number of possible haplotypes in the  genomic region consistent with
genomic region consistent with  . The number of different lists of haplotypes is
. The number of different lists of haplotypes is  A function c of λ(q) is defined as the following equation. The summation of c for all haplotype listing for a subject is always equal to 1 (see Supplementary Information).
A function c of λ(q) is defined as the following equation. The summation of c for all haplotype listing for a subject is always equal to 1 (see Supplementary Information).

where


Let us consider a simple example in which there are N=3 independent genomic regions, and the gene–gene interactions between each pair (r=2) of the N regions are considered. There are three possible θi values, that is, θ1={1, 2}, θ2={2, 3} and θ3={1, 3}. We only consider θ1, that is, {1, 2}. Therefore, α1=1 and α2=2. Let the population frequencies of the haplotypes in the first genomic region be 0.5, 0.2, 0.2 and 0.1, and let those in the second genomic region be 0.6 and 0.4. When considering the first genomic region for the subject, q,  and
and  are the possible haplotype combinations of the second genomic region. Therefore, only
are the possible haplotype combinations of the second genomic region. Therefore, only  outcomes are possible.
outcomes are possible.
From Equation (1), we can calculate:

If θ1=(1, 2), the following four lists of haplotypes are possible:

From Equation (3), function c of the above lists of haplotypes can be calculated as follows:

It must be noted that 
Simulation study
Two-locus disease model
There is a broad spectrum of genetic interaction models. The most general is the two-locus disease model in which two unlinked biallelic loci interact, resulting in nine possible genotypic combinations to produce phenotypes. From the complete enumeration of the two-locus disease models, we have selected nine commonly used models that have been described in detail by others.19 The genotype combinations without any at-risk genotype are allowed to be affected in the simulation at the baseline value (α) with the genotype effect (θ). The genotype effects are described in terms of increasing the chance of disease in which a subject with the risk allele has an increase in the chance of 1+θ relative to a subject without the risk allele. The odds for disease of these models under epistasis are shown in Table 1.
The nine models that were selected for the simulation are (1) Jointly dominant-dominant model (DD): the dominant at-risk allele must be present at both loci to cause the disease. (2) Jointly recessive-recessive model (RR): the disease occurs when the homozygous recessive allele is present at both loci. (3) Jointly recessive-dominant model (RD): the only asymmetric model in our simulation. The disease allele is recessive at locus 1 and dominant at locus 2. (4) Dominant-or-dominant model (DorD): the disease phenotype is expressed when the dominant at-risk allele is present at either of the causative loci. (5) Exclude-odds-ratio model (XOR): the disease phenotype is not expressed if there are zero or two risk alleles at both loci. (6) Threshold model (T): three or more at-risk alleles are required to cause the disease. (7) Modified-threshold model (Tmod): two or more at-risk alleles are required to cause the disease. Full penetrance occurs when three or more at-risk alleles are present. (8) Heterogeneity-of dominant-or-dominant model (h-DorD): this model allows for heterogeneity of phenotypic expression in the DorD model. (9) Heterogeneity-of-recessive-or-recessive model (h-RorR): the model allows for heterogeneity in phenotypic expression in a model in which one or both loci are homozygous recessive. The explanations of these models was described previously in the studies by Neuman and Rick20, Schork et al.21 and Knapp et al.22
Parameterization of the interaction model
The simulations of two interaction loci were conducted in a manner similar to that described by Marchini et al.23 The parameters of the simulation were set to give the marginal effect within the range suggested by empirical studies in humans, namely relative risks of 1.2–2.0.24, 25 Therefore, we set the disease prevalence equal to 0.01 and defined marginal heterozygote odds ratio to the value λ. By setting these marginal parameters, the baseline value, α, and the genotype effects in terms of odds, 1+θ, corresponding to the disease model can be calculated according to the range of allele frequencies (p). We assume equal contribution of two loci, for example, loci A and B; hence, the allele frequencies of the interacting loci are assumed to be the same (pA=pB).
Haplotype simulation
We simulated three unlinked haplotype regions by using a haplotype-based simulation software known as SNAP.26 We assume that markers are in strong LD within the regions, whereas markers from different regions are assumed to be in linkage equilibrium. Two haplotype regions were preset to contain the risk loci, whereas the third haplotype region was not. LD between the risk locus and the other three loci within the haplotype region was set to D′=1. This LD pattern consists of five haplotypes, encoded as 1111, 1211, 1212, 1221 and 2212. For nine models, two haplotype regions (each containing one risk locus) were simulated using the parameter setting as follows: n=250, 500, 1000 or 2000; pA=pB=0.05, 0.1, 0.2 or 0.5 and λ=1.2, 1.5 or 2.0. The non-disease haplotype region was simulated by assigning equal probability haplotypes in the LD block.
Searching for haplotype interaction
The haplotype data were used for pHCR analysis, whereas we ignored the phased genotypic information to produce the unphased genotype data for MDR and FAMHAP analysis. We simulated 1000 replicates for each combination of defined parameters to assess the algorithm performance and performed 1000 permutations to determine the threshold for significance. For MDR and pHCR, the permutation was conducted by reassigning the affected status within each data set. The entire process of both pHCR and MDR was performed to produce the empirical distribution of average prediction error. This distribution was used to estimate the significance level of the prediction error generated from the best haplotype interaction model of the original data set.
For the FAMHAP experiment, all possible locus combinations were allowed in searching for interaction (allcombi, maxregion=2) and 10 000 permutations were conducted to obtain the significance level of each interaction. The nominal threshold α was set to 0.05 for every simulation. The strict definition was considered for correct interaction in which
-
pHCR identified the interaction of both at-risk haplotypes as the best model;
-
MDR identified the interaction of both at-risk loci as the best model; and
-
FAMHAP identified an interaction comprising both at-risk loci with a significant P-value under Bonferroni correction.
In summary, for each interaction model, we simulated 48 different scenarios to see the effect of sample size, causative allele frequency and λ value. For each scenario, 1000 replicates were conducted to assess the power on the basis of 1000 permutations.
Results
Simulation study
In our simulation study, we selected a broad range of disease models to compare the three main algorithms that study gene–gene interaction from simple to complex interaction, for example, asymmetry and heterogeneity. From nine selected models, they can be categorized into four main groups:
-
1
the joint effect (DD, RR and RD);
-
2
recessive/exclusive (h-RorR, XOR);
-
3
dominant (h-DorD, DorD); and
-
4
threshold (T, Tmod)
For joint effect, the RD model represents an asymmetric model. The threshold models represent large effect size models, that is, common diseases. For exclusive recessive and exclusive dominant models, the heterogeneity effect is applied to observe the effect of the heterogeneity in comparison with another similar model of the same group. The simulation results are discussed in terms of the robustness in predicting for epistasis against different models, the effect of sample size, allele frequency and λ value to the power of each algorithm in comparison.
Figure 2 presents the average power of MDR, pHCR and FAMHAP across 48 scenarios of 9 models. The power of analysis is strongly dependent on the model used, which is the same for all three algorithms. For example, power is very low for the XOR model, but is consistently high for the Tmod model. For comparative purposes only, the power of each method is considered high if it is ⩾0.5. Nevertheless, for any given model, power varies between algorithms. MDR has a consistently lower power than do pHCR and FAMHAP. The FAMHAP algorithm has a higher power than do the other two algorithms for the DD, RR, h-DorD, T and Tmod models. Although pHCR has a greater power than does FAMHAP for the RD, XOR, h-RoR and DorD models, the power is considerably low. As pHCR and MDR use the same framework while searching for gene–gene interactions, the gain in power of pHCR over MDR occurs by introducing haplotype into the search framework. This result emphasizes the higher power of haplotype analysis over single locus analysis. It is worth noting that for FAMHAP to detect all of the true interactions, we had to relax the P-value threshold from preset value for all nine models.
The overall power performance. The average power across 48 scenarios of each model is shown. The gray line, Parallel Haplotype Configuration Reduction (pHCR) results; the black line, Multifactor Dimensionality Reduction (MDR) results; and the dashed black line, FAMHAP results for the correct interaction defined by the significance level.
The differences between the algorithms for each model were investigated further by varying the analytical parameters. It was found that the λ value had little effect on power (Supplementary Figure 1), whereas causative allele frequency and sample size had a noticeable effect (Figure 3). The results shown in Figure 3 suggested that power has a stronger correlation with allele frequency than does the sample size. The most robust models seem to be the threshold models (group 4), in which all algorithms have high power when allele frequencies are high. At low allele frequencies, power is dependent on the sample size. MDR is more sensitive to the allele frequency than pHCR and FAMHAP, which show loss of power only at an allele frequency of 0.05. The joint effect models (group 1) showed a higher power than did the recessive/exclusive models (group 2), whereas the dominant models (group 3) showed a higher power than did group 2. The most problematic models are the group 2 models, although the introduction of haplotype shows greater power, but the gain in power is modest.
The power of analysis. The solid lines present the Parallel Haplotype Configuration Reduction (pHCR) results; the dashed lines represent the Multifactor Dimensionality Reduction (MDR) results and the dotted lines represent the FAMHAP results. The row represents the difference in allele frequencies that were varied from the top row (0.05) followed by 0.1, 0.2 and 0.4 (bottom row). Different sample sizes (n cases and n controls) are indicated by a color code where n=250 (black), 500 (red), 1000 (green) and 2000 (blue)). λ was fixed to 2.0 throughout. A full color version of this figure is available at the Journal of Human Genetics journal online.
In group 1, the asymmetric model RD showed a lower power than did the symmetric models (DD and RR), as expected. MDR showed a lower power to detect the true interaction, whereas the haplotype-based methods (pHCR and FAMHAP) could detect the true interaction only when the causative allele frequencies were 0.4.
The effect of heterogeneity can be observed in the dominant models (group 3). Overall, the h-DorD model had higher power than did the DorD model. However, the increase in power when using the h-DorD model was observed only when the allele frequency was ⩾0.1 for pHCR and FAMHAP, whereas MDR showed lower power than did other algorithms when the allele frequency was <0.4.
The false-positive rate for the three algorithms is presented in Table 2. MDR has the lowest overall false-positive rate (average=0.0424), followed by pHCR and then FAMHAP. FAMHAP showed markedly more false positives for some models over the others, whereas MDR and pHCR had similar false-positive rates for different models.
Real data set
Patients with β0-Thalassemia/Hemoglobin E (HbE) show variability in clinical presentations from asymptomatic to severe transfusion dependence. Genetic factors associated with disease severity were identified within the β-globin cluster.27 However, differences in clinical severity have still been observed among patients who have similar β-globin cluster genotype. Thus, an association study including 97 SNPs of 27 candidate genes was performed in 256 β0-Thalassemia/HbE patients with phenotypes classified as either mild or severe according to a severity classification-scoring system.28 The single SNP analysis showed no association with disease severity after multiple testing correction using the false discovery rate method (see Supplementary Table 1).
The pHCR algorithm was used to analyze the genotyping data and to search for possible gene–gene interactions. SNPs with a minor allele frequency <0.05 were excluded from the analysis. LD was observed using Haploview-v.3.2.29 Haplotype blocks were defined using Gabriel's definition.30 SNPs within the same LD block were selected using the Bayesian haplotype inference tool PHASE version 2.1.31 The pHCR algorithm was used to analyze these data, and 1000 permutations were performed to predict the interactions with significance level. The MDR algorithm was tested on this data set using default parameters.
The genetic interactions detected by MDR were insignificant with very low cross-validation, prediction and classification accuracies. FAMHAP analysis was not performed, as the large number of haplotype blocks in this data set would likely generate an unacceptably high number of false positives. On the other hand, significant interactions of biological interest were revealed by pHCR. The best interaction model discovered by pHCR was the 3-model interaction of DEPDC2, PIK3C2A and HBS1L genes. The classification accuracy of this model was 0.6427, whereas the prediction accuracy was 0.5710 (P=0.002). The cross-validation consistency of this model was 7 out of 10. For PIK3C2A, there is no previous report of its relationship to the β-thalassemia disease. However, DEPDC2 and HBS1L, located on chromosome 8 and chromosome 6, respectively, are in the proximity of the previously reported QTL region that associates with the fetal hemoglobin level.32, 33, 34 Thus, the results produced from pHCR analysis are consistent with the known biological factors for this disease, reaffirming the interplay of these two regions.
Discussion
The proposed pHCR algorithm showed its ability to identify haplotype interactions that associate with the disease state. The parallel programming solution was created to handle the analysis of a large number of all possible interaction combinations. The running time (elapsed time) for predicting a 2-interaction model using 500 ‘regions’ was ∼72 min on a computer using CPU Pentium IV, 3.06 GHz, 2 GB RAM (random access memory). However, when using a 50-node cluster computer with the same computer specification running in parallel, the running time reduced dramatically to merely 3 min. It must be noted that the running time in performing permutation tests on the 50-node cluster is ∼1.5 min per permutation.
To achieve better parallelism (running the program in parallel), two important factors need to be minimized (1) communication costs among the processing nodes and (2) the underlying I/O (input/output) operations from each node. The ranked interaction technique was able to overcome these two factors. During program execution, the communication between processing nodes (node synchronization) occurred only twice: first, when the master node assigns the workload to each compute node; and, second, when the results are being collected by the master. Furthermore, the major I/O operations are performed twice while reading the input data and writing the results, both of which are done only by the master node. Through the design of this parallel solution, the ranked interaction scheme can be deployed on larger clusters or even a computational grid without reducing the efficiency of the pHCR program.
In this study, pHCR largely extends the MDR framework by using haplotypes and their probabilities to analyze the best haplotype interaction model. In a simulation study, we would like to observe the power of both algorithms in a worst-case scenario. Therefore, the simulated data were specifically created. Genotypes without the risk allele were allowed to be affected at the baseline value and a strict definition of correct interaction was considered.
When comparing with MDR, the simulation results clearly showed that pHCR possesses higher power to detect the correct gene–gene interaction from all simulated scenarios. The result supported the concept that haplotype-based analysis has higher power over individual SNP analysis. The power to detect epistasis depends on the sample size and the allele frequency. Moreover, the power to detect epistasis is also different under various genetic models. The threshold models are the most robust for detecting gene–gene interactions. In contrast, the recessive/exclusive models have a very low power to detect interactions when used by all three algorithms. pHCR had marked advantage over MDR, particularly for analysis using the heterogeneity and asymmetric models; only MDR showed a decrease in the power to detect the true interaction. This result is consistent with a previous report that MDR has lower power to detect the interaction in the presence of phenocopy, missing data and genetic heterogeneity.35
We compared our approach with Becker's method implemented in FAMHAP. This tool performs χ2 test statistic to capture potential interactions that pass a high confidence probability threshold. This technique, however, does not aim at producing a model that can be used to predict states of the disease. Furthermore, FAMHAP does not explicitly test for each specific interaction model, but rather tests whether unlinked regions, either alone or together with other unlinked regions, show association with the disease. Therefore, under a significant global hypothesis, irrespective of the threshold cutoff used, FAMHAP will report false positives. The false-positive rate of FAMHAP showed an average of all models equal to 0.2659 in our simulation study. Overall, pHCR and FAMHAP showed similar power to detect the correct interactions. Although FAMHAP is likely to be more robust than pHCR for small sample sizes, FAMHAP could not predict the best/overall true interaction.
The advantage of our proposed algorithm is not only in the power to detect the true interaction but also in the ability to accommodate the interpretation of multiple SNPs as a functional unit of gene interactions. pHCR also reported the potential interaction as a haplotype prediction model, which can be used for more challenging tests of independent data sets. On the other hand, the major limitation of this framework is the time required for analysis, which could be impractical for a large number of SNP inputs. Although a parallel scheme is proposed, very large-scale analysis of higher-order interaction, for example, on newer SNP array platforms is still not practical. The two-stage analysis may be a possible solution.23
To our knowledge, many algorithms for detecting gene–gene interactions were presented, yet none of them were adopted as the ‘gold standard’ for gene–gene interaction analysis. A common concern of these approaches is how to model the interaction as well as the biological interpretation of the results. However, we believe that the development of our proposed pHCR algorithm will reveal the hidden gene–gene interaction information that is the predisposing factor to a complex disease.
References
Carlborg, O. & Haley, C. S. Epistasis: too often neglected in complex trait studies? Nat. Rev. Genet. 5, 618–625 (2004).
Culverhouse, R., Suarez, B. K., Lin, J. & Reich, T. A perspective on epistasis: limits of models displaying no main effect. Am. J. Hum. Genet. 70, 461–471 (2002).
Heidema, A. G., Boer, J. M., Nagelkerke, N., Mariman, E. C., van der, A D. L. & Feskens, E. J. The challenge for genetic epidemiologists: how to analyze large numbers of SNPs in relation to complex diseases. BMC Genet. 7, 23 (2006).
Ritchie, M. D., Hahn, L. W., Roodi, N., Bailey, L. R., Dupont, W. D., Parl, F. F. et al. Multifactor-dimensionality reduction reveals high-order interactions among estrogen metabolism genes in sporadic breast cancer. Am. J. Hum. Genet. 69, 138–147 (2001).
Hahn, L. W., Ritchie, M. D. & Moore, J. H. Multifactor dimensionality reduction software for detecting gene-gene and gene-environment interactions. Bioinformatics 19, 376–382 (2003).
Nelson, M. R., Kardia, S. L., Ferrell, R. E. & Sing, CF . A combinatorial partitioning method to identify multilocus genotypic partitions that predict quantitative trait variation. Genome. Res. 11, 458–470 (2001).
Moore, J. H. & Williams, S. M. New strategies for identifying gene-gene interactions in hypertension. Ann. Med. 34, 88–95 (2002).
Cho, Y. M., Ritchie, M. D., Moore, J. H., Park, J. Y., Lee, K. U., Shin, H. D. et al. Multifactor-dimensionality reduction shows a two-locus interaction associated with type 2 diabetes mellitus. Diabetologia 47, 549–554 (2004).
Tsai, C. T., Lai, L. P., Lin, J. L., Chiang, F. T., Hwang, J. J., Ritchie, M. D. et al. Renin-angiotensin system gene polymorphisms and atrial fibrillation. Circulation 109, 1640–1646 (2004).
Martin, E. R., Ritchie, M. D., Hahn, L., Kang, S. & Moore, J. H. A novel method to identify gene-gene effects in nuclear families: the MDR-PDT. Genet. Epidemiol. 30, 111–123 (2006).
Mei, H., Cuccaro, M. L. & Martin, E. R. Multifactor dimensionality reduction phenomics: a novel method to capture genetic heterogeneity with use of phenotypic variables. Am. J. Hum. Genet. 81, 1251–1261 (2007).
Bush, W. S., Edwards, T. L., Dudek, S. M., McKinney, B. A. & Ritchie, M. D. Alternative contingency table measures improve the power and detection of multifactor dimensionality reduction. BMC Bioinformatics 16, 238 (2008).
Pattin, K. A., White, B. C., Barney, N., Gui, J., Nelson, H. H., Kelsey, K. T. et al. A computationally efficient hypothesis testing method for epistasis analysis using multifactor dimensionality reduction. Genet. Epidemiol. 33, 87–94 (2008).
Motsinger-Reif, A. A. The effect of alternative permutation testing strategies on the performance of multifactor dimensionality reduction. BMC Res. Notes 1, 139 (2008).
Clark, A. G. The role of haplotypes in candidate gene studies. Genet. Epidemiol. 27, 321–333 (2004).
Schaid, D. J. Evaluating associations of haplotypes with traits. Genet. Epidemiol. 27, 348–364 (2004).
Morris, R. W. & Kaplan, N. L. On the advantage of haplotype analysis in the presence of multiple disease susceptibility alleles. Genet. Epidemiol. 23, 221–233 (2002).
Becker, T., Schumacher, J., Cichon, S., Baur, M. P. & Knapp, M. Haplotype interaction analysis of unlinked regions. Genet. Epidemiol. 29, 313–322 (2005).
Li, W. & Reich, J. A complete enumeration and classification of two-locus disease models. Hum. Hered. 50, 334–349 (2000).
Neuman, R. J. & Rick, J. P. Two-locus models of disease. Genet. Epidemiol. 9, 347–365 (1992).
Schork, N. J., Boehnke, M., Terwilliger, J. D. & Ott, J. Two-trait-locus linkage analysis: a powerful strategy for mapping complex genetic traits. Am. J. Hum. Genet. 53, 1127–1136 (1993).
Knapp, M., Seuchter, S. A. & Baur, M. P. Two-locus disease models with two marker loci: the power of affected-sib-pair tests. Am. J. Hum. Genet. 55, 1030–1041 (1994).
Marchini, J., Donnelly, P. & Cardon, L. R. Genome-wide strategies for detecting multiple loci that influence complex diseases. Nat. Genet. 37, 413–417 (2005).
Carlson, C. S., Newman, T. L. & Nickerson, D. A. SNPing in the human genome. Curr. Opin. Chem. Biol. 5, 78–85 (2001).
Lohmueller, K. E., Pearce, C. L., Pike, M., Lander, E. S. & Hirschhorn, J. N. Metaanalysis of genetic association studies supports a contribution of common variants to susceptibility to common disease. Nat. Genet. 33, 177–182 (2003).
Nothnagel, M. Simulation of LD block-structured SNP haplotype data and its use for the analysis of case-control data by supervised learning methods. Am. J. Hum. Genet. 71, A2363 (2002).
Ma, Q., Abel, K., Sripichi, O., Whitacre, J., Angkachatachi, V. & Makarasara, W. et al. Beta-globin cluster polymorphisms are strongly associated with severity of HbE/beta(0)-thalassemia. Clin. Genet. 72, 497–505 (2007).
Sripichai, O., Makarasara, W., Munkongdee, T., Kumkhaek, C., Nuchprayoon, I., Chuansumrit, A. et al. A scoring system for the classification of beta-thalassemia/HbE disease severity. Am. J. Hematol. 83, 482–484 (2008).
Barrett, J. C., Fry, B., Maller, J. & Daly, M. J. Haploview: analysis and visualization of LD and haplotype maps. Bioinformatics 21, 263–265 (2005).
Gabriel, S. B., Schaffner, S. F., Nguyen, H., Moore, J. H., Roy, J., Blumenstiel, B. et al. The structure of haplotype blocks in the human genome. Science 296, 2225–2229 (2002).
Stephens, M. & Donnelly, P. A comparison of Bayesian methods for haplotype reconstruction from population genotype data. Am. J. Hum. Genet. 73, 1162–1169 (2003).
Garner, C. P., Tatu, T., Best, S., Creary, L. & Thein, S. L. Evidence of genetic interaction between the beta-globin complex and chromosome 8q in the expression of fetal hemoglobin. Am. J. Hum. Genet. 70, 793–799 (2002).
Garner, C., Menzel, S., Martin, C., Silver, N., Best, S., Sepctor, T. D. et al. Interaction between two quantitative trait loci affects fetal haemoglobin expression. Ann. Hum. Genet. 69, 707–714 (2005).
Thein, S. L., Menzel, S., Peng, X., Best, S., Jiang, J., Close, J. et al. Intergenic variants of HBS1L-MYB are responsible for a major quantitative trait locus on chromosome 6q23 influencing fetal hemoglobin levels in adults. Proc. Natl Acad. Sci. USA 104, 11346–11351 (2007).
Ritchie, M. D., Hahn, L. W. & Moore, J. H. Power of multifactor dimensionality reduction for detecting gene-gene interactions in the presence of genotyping error, missing data, phenocopy, and genetic heterogeneity. Genet. Epidemiol. 24, 150–157 (2003).
Acknowledgements
We thank Dr Nachol Chaiyaratana for the discussions that led to the idea presented in this work. We also thank Dr Philip J Shaw for his insightful comments on the revision of this work. The corresponding author (ST) acknowledges the Thailand Research Fund (TRF) for partially supporting this work. WM acknowledges the Medical Scholar Program, Mahidol University, for supporting her doctoral study. ST, AA, CN and UT thank the National Center for Genetic Engineering and Biotechnology (BIOTEC), National Science and Technology Development Agency (NSTDA) for support in conducting this research. AI thanks the National Electronics and Computer Technology Center. Part of this work was carried out by WM at RIKEN, Yokohama, Japan with the support, in part, of the Department of Medical Sciences, Ministry of Public Health, Thailand, in collaboration with RIKEN, Japan.
Author information
Authors and Affiliations
Corresponding author
Additional information
Supplementary Information accompanies the paper on Journal of Human Genetics website (http://www.nature.com/jhg)
Rights and permissions
About this article
Cite this article
Makarasara, W., Kumasaka, N., Assawamakin, A. et al. pHCR: a Parallel Haplotype Configuration Reduction algorithm for haplotype interaction analysis. J Hum Genet 54, 634–641 (2009). https://doi.org/10.1038/jhg.2009.85
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/jhg.2009.85