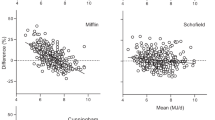
Abstract
Basal metabolic rate (BMR) represents the largest component of total energy expenditure and is a major contributor to energy balance. Therefore, accurately estimating BMR is critical for developing rigorous obesity prevention and control strategies. Over the past several decades, numerous BMR formulas have been developed targeted to different population groups. A comprehensive literature search revealed 248 BMR estimation equations developed using diverse ranges of age, gender, race, fat-free mass, fat mass, height, waist-to-hip ratio, body mass index and weight. A subset of 47 studies included enough detail to allow for development of meta-regression equations. Utilizing these studies, meta-equations were developed targeted to 20 specific population groups. This review provides a comprehensive summary of available BMR equations and an estimate of their accuracy. An accompanying online BMR prediction tool (available at http://www.sdl.ise.vt.edu/tutorials.html) was developed to automatically estimate BMR based on the most appropriate equation after user-entry of individual age, race, gender and weight.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout

Similar content being viewed by others
References
Abdel-Hamid TK . Modeling the dynamics of human energy regulation and its implications for obesity treatment. Syst Dynam Rev 2002; 18: 431–471.
Poehlman ET . Energy expenditure and requirements in aging humans. J Nutr 1992; 122: 2057–2065.
Ferrannini E . The theoretical bases of indirect calorimetry: a review. Metabolism 1988; 37: 287–301.
Bogardus C, Lillioja S, Ravussin E, Abbott W, Zawadzki JK, Young A et al. Familial dependence of the resting metabolic rate. N Engl J Med 1986; 315: 96–100.
Heymsfield SB, Thomas D, Bosy-Westphal A, Shen W, Peterson CM, Muller MJ . Evolving concepts on adjusting human resting energy expenditure measurements for body size. Obes Rev 2012; 13: 1001–1014.
Sherman HC . Chemistry of Food and Nutrition. Macmillan Co.: New York, 1946.
Torun B, Davies P, Livingstone M, Paolisso M, Sackett R, Spurr G . Energy requirements and dietary energy recommendations for children and adolescents 1 to 18 years old. Eur J Clin Nutr 1996; 50 (Suppl 1): S37–S80 discussion S80-1.
Harris J, Benedict F . A biometric Study of Basal Metabolism in Man. Carnegie Institution: Washington, DC, 1919.
Cunningham JJ . A reanalysis of the factors influencing basal metabolic rate in normal adults. Am J Clin Nutr 1980; 33: 2372–2374.
Maffeis C, Schutz Y, Micciolo R, Zoccante L, Pinelli L . Resting metabolic rate in six- to ten-year-old obese and nonobese children. J Pediatr 1993; 122: 556–562.
Vaughan L, Zurlo F, Ravussin E . Aging and energy expenditure. Am J Clin Nutr 1991; 53: 821–825.
Speakman JR, Westerterp KR . Associations between energy demands, physical activity, and body composition in adult humans between 18 and 96 y of age. Am J Clin Nutr 2010; 92: 826–834.
Cunningham J . Body composition as a determinant of energy expenditure: a synthetic review and a proposed general prediction equation. Am J Clin Nutr 1991; 54: 963–969.
Tershakovec AM, Kuppler KM, Zemel B, Stallings VA . Age, sex, ethnicity, body composition, and resting energy expenditure of obese African American and white children and adolescents. Am J Clin Nutr 2002; 75: 867–871.
Bhopal RS, Rafnsson SB . Could mitochondrial efficiency explain the susceptibility to adiposity, metabolic syndrome, diabetes and cardiovascular diseases in South Asian populations? Int J Epidemiol 2009; 38: 1072–1081.
Frankenfield D, Roth-Yousey L, Compher C . Comparison of predictive equations for resting metabolic rate in healthy nonobese and obese adults: a systematic review. J Am Diet Assoc 2005; 105: 775–789.
Mifflin MD, Jeor ST, Hill LA, Scott BJ, Daugherty SA, Koh YO . A new predictive equation for resting energy expenditure in healthy individuals. Am J Clin Nutr 1990; 51: 241–247.
Owen OE, Holup JL, D’Alessio DA, Craig ES, Polansky M, Smalley KJ et al. A reappraisal of the caloric requirements of men. Am J Clin Nutr 1987; 46: 875–885.
Owen OE, Kavle E, Owen RS, Polansky M, Caprio S, Mozzoli MA et al. A reappraisal of caloric requirements in healthy women. Am J Clin Nutr 1986; 44: 1–19.
WHO. Energy and protein requirements. Report of a joint FAO/WHO/UNU Expert Consultation. World Health Organ Tech Rep Ser 1985; 724: 1–206.
Wang Z, Heshka S, Gallagher D, Boozer CN, Kotler DP, Heymsfield SB . Resting energy expenditure-fat-free mass relationship: new insights provided by body composition modeling. Am J Physiol Endocrinol Metab 2000; 279: E539–E545.
Johannsen DL, Knuth ND, Huizenga R, Rood JC, Ravussin E, Hall KD . Metabolic slowing with massive weight loss despite preservation of fat-free mass. J Clin Endocrinol Metab 2012; 97: 2489–2496.
Hall KD . Modeling metabolic adaptations and energy regulation in humans. Annu Rev Nutr 2012; 32: 35–54.
Becker BJ, Wu MJ . The synthesis of regression slopes in meta-analysis. Stat Sci 2007; 22: 414–429.
Nelson J, Kennedy P . The use (and abuse) of meta-analysis in environmental and natural resource economics: an assessment. Environ Resource Eco 2009; 42: 345–377.
Bini LM, Coelho AS, Diniz-Filho JA . Is the relationship between population density and body size consistent across independent studies? A meta-analytical approach. Braz J Biol 2001; 61: 1–6.
Manning AK, LaValley M, Liu C-T, Rice K, An P, Liu Y et al. Meta-analysis of gene-environment interaction: joint estimation of SNP and SNP × environment regression coefficients. Genet Epidemiol 2011; 35: 11–18.
Ros GH, Temminghoff EJM, Hoffland E . Nitrogen mineralization: a review and meta-analysis of the predictive value of soil tests. Eur J Soil Sci 2011; 62: 162–173.
IOM. Dietary Reference Intakes for Energy, Carbohydrate, Fiber, Fat, Fatty Acids, Cholesterol, Protein, and Amino Acids (Macronutrients). Institute of Medicine of the National Academies: Washington, DC, 2005.
St-Onge MP, Gallagher D . Body composition changes with aging: the cause or the result of alterations in metabolic rate and macronutrient oxidation? Nutrition 2010; 26: 152–155.
Wang Z, Heshka S, Heymsfield SB, Shen W, Gallagher D . A cellular-level approach to predicting resting energy expenditure across the adult years. Am J Clin Nutr 2005; 81: 799–806.
Hall KD, Sacks G, Chandramohan D, Chow CC, Wang YC, Gortmaker SL et al. Quantification of the effect of energy imbalance on bodyweight. Lancet 2011; 378: 826–837.
Schwartz GE . Estimating the dimension of a model. Ann Statist 1978; 6: 461–464.
Akaike H . A new look at the statistical model identification. IEEE Trans Automat Contr 1974; 19: 716–723.
Molnar D, Jeges S, Erhardt E, Schutz Y . Measured and predicted resting metabolic rate in obese and nonobese adolescents. J Pediatr 1995; 127: 571–577.
Lazzer S, Agosti F, De Col A, Sartorio A . Development and cross-validation of prediction equations for estimating resting energy expenditure in severely obese Caucasian children and adolescents. Br J Nutr 2006; 96: 973–979.
Lazzer S, Bedogni G, Lafortuna CL, Marazzi N, Busti C, Galli R et al. Relationship between basal metabolic rate, gender, age, and body composition in 8,780 white obese subjects. Obesity (Silver Spring) 2010; 18: 71–78.
Garby L, Garrow JS, Jorgensen B, Lammert O, Madsen K, Sorensen P et al. Relation between energy expenditure and body composition in man: specific energy expenditure in vivo of fat and fat-free tissue. Eur J Clin Nutr 1988; 42: 301–305.
Sun M, Gower BA, Nagy TR, Trowbridge CA, Dezenberg C, Total GoranMI . resting, and activity-related energy expenditures are similar in Caucasian and African-American children. Am J Physiol 1998; 274 (2 Pt 1): E232–E237.
Kaplan AS, Zemel BS, Stallings VA . Differences in resting energy expenditure in prepubertal black children and white children. J Pediatr 1996; 129: 643–647.
DeLany JP, Bray GA, Harsha DW, Volaufova J . Energy expenditure in preadolescent African American and white boys and girls: the Baton Rouge Children’s Study. Am J Clin Nutr 2002; 75: 705–713.
Bosy-Westphal A, Wolf A, Buhrens F, Hitze B, Czech N, Monig H et al. Familial influences and obesity-associated metabolic risk factors contribute to the variation in resting energy expenditure: the Kiel Obesity Prevention Study. Am J Clin Nutr 2008; 87: 1695–1701.
Wren RE, Blume H, Mazariegos M, Solomons N, Alvarez JO, Goran MI . Body composition, resting metabolic rate, and energy requirements of short- and normal-stature, low-income Guatemalan children. Am J Clin Nutr 1997; 66: 406–412.
Bernstein RS, Thornton JC, Yang MU, Wang J, Redmond AM, Pierson RN et al. Prediction of the resting metabolic rate in obese patients. Am J Clin Nutr 1983; 37: 595–602.
Huang KC, Kormas N, Steinbeck K, Loughnan G, Caterson ID . Resting metabolic rate in severely obese diabetic and nondiabetic subjects. Obes Res 2004; 12: 840–845.
Javed F, He Q, Davidson LE, Thornton JC, Albu J, Boxt L et al. Brain and high metabolic rate organ mass: contributions to resting energy expenditure beyond fat-free mass. Am J Clin Nutr 2010; 91: 907–912.
Piers LS, Soares MJ, McCormack LM, O’Dea K . Is there evidence for an age-related reduction in metabolic rate? J Appl Physiol 1998; 85: 2196–2204.
Welle S, Forbes GB, Statt M, Barnard RR, Amatruda JM . Energy-expenditure under free-living conditions in normal-weight and overweight women. Am J Clin Nutr 1992; 55: 14–21.
Foster GD, Wadden TA, Vogt RA . Resting energy expenditure in obese African American and Caucasian women. Obes Res 1997; 5: 1–8.
Bronstein MN, Mak RP, King JC . Unexpected relationship between fat mass and basal metabolic rate in pregnant women. Br J Nutr 1996; 75: 659–668.
Soares MJ, Piers LS, O’Dea K, Collier GR . Plasma leptin concentrations, basal metabolic rates and respiratory quotients in young and older adults. Int J Obes Relat Metab Disord 2000; 24: 1592–1599.
Nelson KM, Weinsier RL, Long CL, Schutz Y . Prediction of resting energy expenditure from fat-free mass and fat mass. Am J Clin Nutr 1992; 56: 848–856.
Ravussin E, Rising R . Daily energy expenditure in humans: measurements in a respiratory chamber and by doubly labeled water. In: Kinney JM e (eds). Energy Metabolism: Tissue Determinants and Cellular Corollaries. Raven Press: New York, NY, 1992. pp 81–96.
Jensen MD, Braun JS, Vetter RJ, Marsh HM . Measurement of body potassium with a whole-body counter: relationship between lean body mass and resting energy expenditure. Mayo Clin Proc 1988; 63: 864–868.
Heshka S, Yang MU, Wang J, Burt P, Pi-Sunyer FX . Weight loss and change in resting metabolic rate. Am J Clin Nutr 1990; 52: 981–986.
Weigle DS, Sande KJ, Iverius PH, Monsen ER, Brunzell JD . Weight loss leads to a marked decrease in nonresting energy expenditure in ambulatory human subjects. Metabolism 1988; 37: 930–936.
Pannemans DL, Westerterp KR . Energy expenditure, physical activity and basal metabolic rate of elderly subjects. Br J Nutr 1995; 73: 571–581.
Tataranni PA, Ravussin E . Variability in metabolic rate: biological sites of regulation. Int J Obes Relat Metab Disord 1995; 19 (Suppl 4): S102–S106.
Blanc S, Schoeller DA, Bauer D, Danielson ME, Tylavsky F, Simonsick EM et al. Energy requirements in the eighth decade of life. Am J Clin Nutr 2004; 79: 303–310.
De Lorenzo A, Andreoli A, Bertoli S, Testolin G, Oriani G, Deurenberg P . Resting metabolic rate in Italians: relation with body composition and anthropometric parameters. Acta Diabetol 2000; 37: 77–81.
Ferraro R, Lillioja S, Fontvieille AM, Rising R, Bogardus C, Ravussin E . Lower sedentary metabolic-rate in women compared with men. J Clin Invest 1992; 90: 780–784.
Hunter GR, Weinsier RL, Gower BA, Wetzstein C . Age-related decrease in resting energy expenditure in sedentary white women: effects of regional differences in lean and fat mass. Am J Clin Nutr 2001; 73: 333–337.
Ganpule AA, Tanaka S, Ishikawa-Takata K, Tabata I . Interindividual variability in sleeping metabolic rate in Japanese subjects. Eur J Clin Nutr 2007; 61: 1256–1261.
Gallagher D, Albu J, He Q, Heshka S, Boxt L, Krasnow N et al. Small organs with a high metabolic rate explain lower resting energy expenditure in African American than in white adults. Am J Clin Nutr 2006; 83: 1062–1067.
Fontvieille AM, Ferraro RT, Rising R, Larson DE, Ravussin E . Energy-cost of arousal–effect of sex, race and obesity. Int J Obes 1993; 17: 705–709.
Kunz I, Schorr U, Klaus S, Sharma AM . Resting metabolic rate and substrate use in obesity hypertension. Hypertension 2000; 36: 26–32.
Nielsen S, Hensrud DD, Romanski S, Levine JA, Burguera B, Jensen MD . Body composition and resting energy expenditure in humans: role of fat, fat-free mass and extracellular fluid. Int J Obes Relat Metab Disord 2000; 24: 1153–1157.
Wyatt HR, Grunwald GK, Seagle HM, Klem ML, McGuire MT, Wing RR et al. Resting energy expenditure in reduced-obese subjects in the National Weight Control Registry. Am J Clin Nutr 1999; 69: 1189–1193.
Horie LM, Gonzalez MC, Torrinhas RS, Cecconello I, Waitzberg DL . New Specific equation to estimate resting energy expenditure in severely obese patients. Obesity (Silver Spring) 2011; 19: 1090–1094.
Weinsier RL, Nelson KM, Hensrud DD, Darnell BE, Hunter GR, Schutz Y . Metabolic predictors of obesity - contribution of resting energy-expenditure, thermal effect of food, and fuel utilization to 4-year weight-gain of post-obese and never-obese women. J Clin Invest 1995; 95: 980–985.
Luhrmann PM, Bender R, Edelmann-Schafer B, Neuhauser-Berthold M . Longitudinal changes in energy expenditure in an elderly German population: a 12-year follow-up. Eur J Clin Nutr 2009; 63: 986–992.
Luhrmann PM, Edelmann-Schafer B, Neuhauser-Berthold M . Changes in resting metabolic rate in an elderly German population: cross-sectional and longitudinal data. J Nutr Health Aging 2010; 14: 232–236.
Piers LS, Shetty PS . Basal metabolic rates of Indian women. Eur J Clin Nutr 1993; 47: 586–591.
Soares MJ, Francis DG, Shetty PS . Predictive equations for basal metabolic rates of Indian males. Eur J Clin Nutr 1993; 47: 389–394.
Dellabianca P, Jequier E, Schutz Y . Lack of metabolic and behavioral adaptations in rural gambian men with low body-mass index. Am J Clin Nutr 1994; 60: 37–42.
Luke A, Rotimi CN, Adeyemo AA, Durazo-Arvizu RA, Prewitt TE, Moragne-Kayser L et al. Comparability of resting energy expenditure in Nigerians and U.S. blacks. Obes Res 2000; 8: 351–359.
Aleman-Mateo H, Salazar G, Hernandez-Triana M, Valencia ME . Total energy expenditure, resting metabolic rate and physical activity level in free-living rural elderly men and women from Cuba, Chile and Mexico. Eur J Clin Nutr 2006; 60: 1258–1265.
Acknowledgements
We thank the editor and three anonymous reviewers for their constructive feedback. Participants in the National Collaborative on Childhood Obesity Research (NCCOR) Envision’s Comparative Modeling Network (CompMod) program provided helpful comments. Financial Support Provided through Envision’s CompMod program and NIH Office of Behavioral and Social Sciences Research (OBSSR) contract: HHSN276201000004C.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies this paper on International Journal of Obesity website
Supplementary information
Rights and permissions
About this article
Cite this article
Sabounchi, N., Rahmandad, H. & Ammerman, A. Best-fitting prediction equations for basal metabolic rate: informing obesity interventions in diverse populations. Int J Obes 37, 1364–1370 (2013). https://doi.org/10.1038/ijo.2012.218
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/ijo.2012.218
Keywords
This article is cited by
-
Comparison of energy expenditure measurements by a new basic respiratory room vs. classical ventilated hood
Nutrition Journal (2023)
-
Factors related to hypermetabolism in individuals with type 2 diabetes mellitus and non-alcoholic fatty liver disease
Scientific Reports (2023)
-
Accuracy of Resting Metabolic Rate Prediction Equations in Athletes: A Systematic Review with Meta-analysis
Sports Medicine (2023)
-
Review on modelling approaches of thermoregulation mechanisms
Journal of Thermal Analysis and Calorimetry (2023)
-
A century of exercise physiology: concepts that ignited the study of human thermoregulation. Part 2: physiological measurements
European Journal of Applied Physiology (2023)