Abstract
During the last years, simple sequence repeats (SSRs, also known as microsatellites) and single-nucleotide polymorphisms (SNPs) have become the most popular molecular markers for describing neutral genetic variation in populations of a wide range of organisms. However, only a limited number of studies has focused on comparing the performance of these two types of markers for describing the underlying genetic structure of wild populations. Moreover, none of these studies targeted fungi, the group of organisms with one of the most complex reproductive strategies. We evaluated the utility of SSRs and SNPs for inferring the neutral genetic structure of Armillaria cepistipes (basidiomycetes) at different spatial scales. For that, 407 samples were collected across a small (150 km2) area in the Ukrainian Carpathians and a large (41 000 km2) area in the Swiss Alps. All isolates were analyzed at 17 SSR loci distributed throughout the whole genome and at 24 SNP loci located in different single-copy conserved genes. The two markers showed different patterns of structure within the two spatial scales studied. The multi-allelic SSR markers seemed to be best suited for detecting genetic structure in indigenous fungal populations at a rather small spatial scale (radius of ~50–100 km). The pattern observed at SNP markers rather reflected ancient divergence of distant (~1000 km) populations that in addition are separated by mountain ranges. Despite these differences, both marker types were suitable for detecting the weak genetic structure of the two A. cepistipes populations investigated.
Similar content being viewed by others
Introduction
Investigating the population genetics of fungi may be a challenging task because of the complexity of their mating systems (for example, Nieuwenhuis and James, 2016). Besides sexual reproduction and clonal (asexual) spread, diploid–haploid mating resulting in the formation of a recombinant nucleus through complex events may also be observed. These different mating processes can occur in parallel and have contradictory impacts on traditional population genetic estimators like heterozygosity (De Meeûs et al., 2007). Potentially, this may lead to false inferences, for example, revealing subdivisions in populations which are actually not subdivided or extensive genetic exchange when it is completely absent. In the recent past, in addition to traditional population genetic estimators, a range of clustering methods for probabilistically assigning individuals to genetic clusters have been developed (Pritchard et al., 2000; Jombart et al., 2010). Although these methods have been used with a variety of molecular markers, so far only a limited number of studies exists that compared the particular outcome of depicting population genetic structure with different markers types, particularly in fungal study systems. On one hand, the different reproductive processes mentioned above act on the entire nuclear genome, therefore, we expect them to have a similar impact on different marker types. On the other hand, although these clustering methods are based on allele frequencies and do not directly include the characteristics (like mutation rate or ascertainment bias, see below) of the applied markers, we might expect differences in population structure inference when using them, because different marker types can exhibit different spectra of allele frequencies (see, for example, Fischer et al., 2017).
During the last two decades, simple sequence repeats (SSRs, also known as microsatellites) and single-nucleotide polymorphisms (SNPs) have become the most popular molecular markers for describing genetic variation in natural populations of a wide range of organisms with different biology. At the same time, an intense debate has arisen about the robustness and consistency of the results obtained with these two types of markers (Väli et al., 2008; Coates et al., 2009; Ljungqvist et al., 2010; Guichoux et al., 2011; Fischer et al., 2017). Both SSRs and SNPs are abundant in the genome of most organisms and therefore potentially useful for detecting the population genetic structure and reconstructing the evolutionary history of species. However, because of different mutation rates and mechanisms, genome-wide distribution patterns and biological functions, the use of SSRs and SNPs may lead to substantially different outcomes when testing specific hypotheses (Banke and McDonald, 2005; Coates et al., 2009; Fischer et al., 2017).
SSRs are generally abundant and polymorphic in non-expressed genomic regions and consequently considered to be selectively neutral. However, SSR loci can also occur in regions of chromosomes (for example, telomeres or centromeres) involved in gene transcription, translation, chromatin organization or recombination (Li et al., 2002) and might therefore be under selection. Neutral SSRs evolve rapidly without vital consequences for the organisms. Due to replication slippage, SSR loci mutate from 10 to 100 thousand times more frequently per generation than single-nucleotide substitutions occur (Guichoux et al., 2011). Their high mutation rates and assumed neutral evolution allow the accumulation of numerous population-specific (that is, private) alleles, which are important for revealing hidden population structure. Their multi-allelic nature also results in a higher probability to detect heterozygosity than, for instance, an equal number of bi-allelic markers. However, the unusual high variability of SSRs in respect to other genomic regions might not necessarily reflect patterns of genome-wide genetic diversity (Väli et al., 2008; Ljungqvist et al., 2010; Fischer et al., 2017). Moreover, the rapid mutation rates of SSRs may also confound signals of population structuring and divergence. For instance, the frequent forward and backward mutations of SSR loci can create identical alleles in populations that are unrelated or genetically isolated (that is, homoplasy). This undesirable effect can be compensated by increasing the number of polymorphic SSR loci used, but the level of genetic differentiation of populations that diverged long time ago could still be underestimated (Estoup et al., 2002).
In recent years, SNPs have started to replace SSRs in population genetic studies as well as in a wide range of other applications (Brumfield et al., 2003; Guichoux et al., 2011). SNPs occur twice as frequently in intergenic and non-coding regions of the genome than in coding regions (Zhao et al., 2003). However, genome-wide association studies revealed that SNPs located in non-coding regions are often physically linked to functional or regulatory genomic sites, thus reflecting, for example, selection signatures (Kim et al., 2007). Given that SNPs are mostly bi-allelic, traditional population genetic statistics can easily be applied to them but a higher number of loci sufficiently polymorphic might be necessary to reach the same power as multi-allelic SSR loci (Guichoux et al., 2011). The advent of next generation sequencing techniques has considerably accelerated, simplified and automated genome-wide SNP detection and genotyping. However, considering that also a relatively low number of highly polymorphic SNPs can potentially give a similar genetic resolution as randomly chosen and multi-allelic SSRs (Kaiser et al., 2016), an alternative strategy to genome-wide SNP screening might be targeting polymorphic sites in unlinked single-copy genes, generally known to be conserved in the targeted phylum (Dutech et al., 2016).
In the present study, we aimed at evaluating the use of SSRs and SNPs for inferences of neutral population genetic structure in the fungus Armillaria cepistipes (Basidiomycota and Physalacriaceae). Fungi of this genus belong to the most important and frequent component of the wood-decaying mycoflora in natural and managed forest ecosystems worldwide (Baumgartner et al., 2011). Moreover, several Armillaria species can act as primary or secondary pathogens causing root rot on a wide range of tree and shrub species, thereby affecting crop and timber plantations. Armillaria has both sexual and asexual (vegetative) reproductive strategies. In addition, diploid–haploid mating was observed for this fungi in vitro (Carvalho et al., 1995). This can create new genotypes in natural populations and potentially alter population structure. Due to vegetative propagation, genotypes (that is, genets) of Armillaria may persist over centuries and even millennia in natural forests. Because of this high longevity and the stable territoriality, Armillaria may influence forest structure and dynamics over several generations of host trees. The preferentially saprophytic A. cepistipes is widely distributed in Europe and frequently occurs in mountain forests from the Alps to the Carpathians (Heinzelmann et al., 2012; Tsykun et al., 2012). Armillaria cepistipes spreads locally by producing a dense network of vegetative rhizomorphs in the soil, through which it can rapidly colonize new food bases (for example, fresh stumps or wood debris). The fungus might also spread over longer distances with wind via basidiospores. These two different strategies of dispersal might have an impact on population genetic structure and different genetic markers may therefore be necessary to reveal it at different spatial scales.
We developed two sets of molecular markers for A. cepistipes; 24 SNPs, each from a different single-copy gene, and 17 SSRs partially derived from a draft genome assembly. We tested these markers on populations with different spatial scales from two European mountain ranges, that is, a large-scaled population scattered over the Swiss Alps and a small-scaled population in two forest locations of the Ukrainian Carpathians (Figure 1). The questions we addressed were: (1) are the two sets of developed markers sufficient for depicting population genetic structure? (2) do SNP and SSR markers produce similar results regarding genetic differentiation and structure, and if not, (3) what are the possible reasons for that?
Geographic origin of the Armillaria cepistipes populations sampled in the Alps (Switzerland) and in the Carpathian mountains (Ukraine). In the lower left part of the figure, the Alpine population is shown, with the white drops indicating isolates of the North subpopulation and the green drops isolates of the South subpopulation. In the lower right part, the Carpathian population is illustrated, with the blue drops representing isolates sampled within plots (a zoomed example is shown) of the Beech subpopulation and the orange drops isolates within plots (a zoomed example is shown) of the Mixed/conifer subpopulation.
Materials and methods
Samples of Armillaria cepistipes
In total, 407 samples of A. cepistipes were used in this study, all originating either from the Carpathians or the Alps (Figure 1). In the Carpathians, samples were collected across 150 km2 in two different protected forests as described in Tsykun et al. (2012), that is, 121 samples within 40 plots in a virgin pure beech (Fagus sylvatica) forest and 160 samples in 35 plots in a natural mixed forest with conifers (Picea abies, Abies alba, Acer pseudoplatanus and Fagus sylvatica). These two Carpathian subpopulations (forests) were about 50 km apart (Figure 1). The pure beech forest is located between 400 and 1150 m a.s.l. The annual average temperature is +7 °C and the annual average precipitation sum is 948 mm. The natural conifer and mixed forest lies between 700 and 1550 m a.s.l. The territory has average temperatures from 0 to +7 °C and the average precipitation sum varies between 1000 and 1500 mm. In both Carpathian forests, Armillaria was systematically sampled on a 1.5 × 1.5 km square grid (Tsykun et al., 2012). In each intersecting point of the grid, a 20 × 25 m (500 m2) plot was established and rhizomorphs were sampled from the soil and from the root collar of trees at all four corners of the rectangle. In Switzerland, an individual-based sampling approach was adopted as described in Heinzelmann et al. (2012). Here, the A. cepistipes samples were collected in managed and unmanaged forests in an area of ~41 000 km2 (Figure 1) covering all altitudinal zones, both north (that is, 62 isolates from the subpopulation Plateau in Heinzelmann et al. (2012)) and within or south of the Alps (64 isolates from the subpopulations Southern, Western Inner, Eastern Inner Alps in Heinzelmann et al. (2012)). These four investigated subpopulations are named as follows: ‘Beech’ and ‘Mixed/conifer’ (for the subpopulations of the Carpathians), and ‘North’ and ‘South’ (for the subpopulations of the Alps).
DNA was extracted as described in Heinzelmann et al. (2012) and Tsykun et al. (2012). All 407 isolates were genotyped with SSRs and SNPs.
Screening and genotyping of SSRs and SNPs
In brief, 32 single copy protein-coding genes of 12 A. cepistipes samples were sequenced and screened for the presence of SNPs (Dutech et al., 2016). Initially, 131 primer pairs amplifying each one SNP were designed and dispatched in multiplexes with MASSARRAY ASSAY DESIGN 4.1 for Sequenom screening. These multiplexes were tested with 48 samples from the Ukrainian Carpathians and 47 samples from the Swiss Alps. SNPs in genes that showed evidence to be present in multiple copies in the genome of A. cepistipes, monomorphic loci (minor allele frequency<5%), and loci that were not amplified in the majority of the screened samples were discarded. After considering the compatibility of the primers pairs, one multiplex of 31 SNPs located in 24 single copy protein-coding genes was selected for final genotyping (for more details, see Supplementary Table S1.1 and Supplementary Figure S1.1, Appendix 1). SNP genotyping was performed using the medium throughput MassARRAY iPLEX genotyping assay from Sequenom (Agena Biosciences, San Diego, CA, USA). Raw genotypic data were analyzed with TYPER 4.0 (Agena Biosciences). In order to test the repeatability of the genotyping, 32 of the 407 DNA isolates were analyzed twice.
A total of 17 SSR loci were used in this study (Supplementary Table S1.2, Appendix 1). Six of them (Arm02, Arm05, Arm09, Arm11, Arm15 and Arm16) were previously specifically developed for A. cepistipes by Prospero et al. (2010). Two loci (Am109 and Am111) were initially developed for A. mellea (Baumgartner et al., 2009) but successfully applied in A. cepistipes (Heinzelmann et al., 2012). The remaining nine loci (AC18, AC31, AC37, AC12, AC16, AC04, AC38, AC22 and AC34) were developed in the present study (for fragment sequences of the selected SSR loci and for annotations see Supplementary Table S1.2, Appendix 1). An A. cepistipes draft genome assembly (G. Sipos, unpublished) was screened for SSR patterns with UNIPRO UGENE v1.170 (Okonechnikov et al., 2012). Search parameters included a nucleotide repeat size of two to six and a minimum tandem length of eight repeats. Among the SSRs detected, 24 loci scattered over 14 major assembled scaffolds were selected. Di-, tri-, tetra- and penta-nucleotide repeats were chosen. SSR loci that might be involved in chromosomal organization and recombination were avoided by ignoring tandem repeats close to telomere regions and repeats in a dense cluster, which might indicate centromere sites (Li et al., 2002).
For each of the 24 selected SSR loci, specific PCR reverse and forward primers were designed using UNIPRO UGENE v1.170 fulfilling the following criteria: GC content of 50–60%, start with G or C, primer size of 20–27 bp, similar annealing temperature (60±3 °C) of forward and reverse primer and a resulting fragment size of 150–400 bp. Initially, each SSR locus was amplified using a forward primer with an M13pa (5′-CACGACGTTGTAAAACGAC-3′) tail, the designed reverse primer and an universal fluorescent dye-labeled M13pa (Boutin-Ganache et al., 2001). Each primer pair was tested separately with four isolates from the Ukrainian Carpathians and three isolates from the Swiss Alps. The PCR program was set as follows: 95 °C (5 min), then 28 cycles at 95 °C (30 s)/60 °C (90 s)/72 °C (30 s), followed by 8 cycles 95 °C (30 s)/55 °C (45 s)/72 °C (30 s), and a final extension at 60 °C for 30 min. PCR products were initially scored for successful amplification on 1.2% agarose gels, and subsequently run on an ABI 3130 Genetic Analyzer using GeneScan LIZ500 (Applied Biosystems, Foster City, CA, USA) as internal size standard. For each locus that was successfully amplified with the M13pa labeled primer, the designed forward primer was then labeled at the 5′-end with a fluorescent dye (6FAM-blue, NED-yellow, VIC-green and PET-red, Applied Biosystems). Four multiplexes including each three to four primer pairs were subsequently developed (Supplementary Table S1.2, Appendix 1). The final PCR was run as follows: 95 °C (15 min), followed by 30 cycles at 94 °C (30 s)/60 °C (90 s)/72 °C (30 s), and a final extension at 60 °C for 30 min and 72 °C for 30 min. The amplified fragments were run on an ABI DNA Analyzer (Applied Biosystems). Alleles were scored with GENEMAPPER 3.7 (Applied Biosystems).
Data analysis
In order to assess and compare the utility of the two marker types, only the isolates with an almost complete SSR and SNP data set (that is, not more than 5% missing data in both marker types) were included in the analyses. To remove a putative clonal effect on the genetic structure, only one representative of each multilocus genotype (MLG) per sampling plot was considered for genetic analysis for SNPs and SSRs separately.
In each population, number (Na) and evenness (E) of alleles per SSR locus, and observed and expected heterozygosity (Hobs and Hexp) for SSR and SNP loci were estimated using ARLEQUIN 3.5.2.1 (Excoffier et al., 2009) and the R-package POPPR (Kamvar et al., 2014). Allelic richness (Ar) per SSR locus was estimated using FSTAT 2.9.3.2 (Goudet, 2002) and rarefied to the population with the lowest sample size (that is, the North Alpine subpopulation with 62 isolates). SSR and SNP loci were tested for significant departure from Hardy–Weinberg equilibrium by conducting a Fisher’s exact test with a Markov chain algorithm (1 000 000 chain steps, 100 000 de-memorization steps) in ARLEQUIN 3.5.2.1. Pairwise linkage disequilibrium between loci was tested with the log-likelihood ratio using a Markov chain algorithm (default parameters) as implemented in the web version of GENEPOP 4.2 (Rousset, 2008). The statistical significance (for Hardy–Weinberg equilibrium and linkage disequilibrium) was inferred using 1000 permutations and sequential Bonferroni correction with α=0.05. Multilocus linkage disequilibrium was evaluated based on the P-values from one-sided permutation tests with the R-package POPPR for the indices of association IA and rbarD (Agapow and Burt, 2001). Genetic differentiation among populations was assessed by calculating pairwise FST-values (Weir and Cockerham, 1984) and corresponding P-values (α=0.05) with ARLEQUIN 3.5.2.1.
Investigating the neutral genetic structure and demographic history of populations implies the use of loci whose population-specific allele frequencies are not affected by natural selection. Although SSR loci are commonly considered as neutral makers, recent studies suggest that this is not always the case (for example, Li et al., 2002). The SNPs used in this study originated from putatively functional genes (Dutech et al., 2016). Thus, allele frequencies at these loci might be driven by natural selection instead of reflecting neutral population processes. Therefore, the SSR and SNP loci used in this study were tested for deviation from neutral patterns using two statistical approaches as implemented in ARLEQUIN 3.5.2.1 and BAYESCAN v2.1 (Foll and Gaggiotti, 2008). The tests were conducted for the Carpathian and Alpine populations, ignoring subpopulations, and separately within the mountain ranges for the two subpopulations each. Both approaches assume a non-hierarchical finite island migration model.
The neutral genetic structure in the four subpopulations was investigated using two different approaches. First, a multivariate clustering method (discriminant analysis of principle components (DAPC)) was applied that identifies synthetic variables and builds discriminant functions maximizing the variation between groups but minimizing it within groups (Jombart et al., 2010). In a first step, genetic data from both marker sets were separately transformed into principal components (PCs) and the optimal number of PCs was assessed with cross-validation (Jombart et al., 2010). Thereafter, we pre-defined geographic groups (that is, the four subpopulations), following the approach previously applied in a population genetic study of the oomycete pathogen Phytophthora infestans (Wang et al., 2017). The DAPC then probabilistically assigned individuals to one of the four pre-defined groups. The analysis was performed with the R-package ADEGENET (Jombart et al., 2010).
We also performed a Bayesian model-based cluster analysis with STRUCTURE 2.3.4 that uses allele frequencies at each locus to probabilistically assign individuals to genetic clusters. We used sampling locations of the subpopulations as prior geographic information (LOCPRIOR), the admixture ancestral model with correlated allele frequencies and indication of null alleles (RECESSIVEALLELES settings) in locus AC18. Analyses were run with 200 000 burn-in iterations followed by the same number of iterations for Markov chain Monte Carlo in 10 independent runs for each number of clusters (K) from 1 to 20. The most likely K was determined by (a) considering the maximal mean and small s.d. of the posterior probability of K among runs (Pritchard et al., 2000) using STRUCTURE HARVESTER (Earl and vonHoldt, 2011) and (b) looking at the alterations of individual assignment probabilities with increasing K (that is, whether additional clusters were reflected by whole individuals or whether they rather resulted in individuals represented by several clusters). Average assignment probabilities of MLGs to the clusters were computed with CLUMPP 1.1.2 (Jakobsson and Rosenberg, 2007) using the Greedy algorithm for K⩾10 and visualized using DISTRUCT 1.1 (Rosenberg, 2004) and R graphic functions.
Results
SNP and SSR marker sets
A total of 117 (89%) out of the 131 detected SNP loci in the 24 single copy protein-coding genes were successfully amplified in the majority (78%) of the samples. Among these, 31 were selected for genotyping (Supplementary Table S2.1, Appendix 2) based on the criteria described in the Materials and Methods section. In the selected set of loci, genotyping was successful in 97% of the samples and repeated genotyping of 32 samples revealed <1% difference in allele calling. All 31 SNP loci were bi-allelic, and in 29 of them the minor allele frequency was above 5%.
Based on the selection criteria given in the Materials and Methods section, a total of 281 SSR loci were found across the draft genome assembly (total length of ~75 Mbp; Münsterkötter et al., 2015). Twelve out of the 24 loci, for which specific primers with the M13pa modification at the 5′-end were designed, successfully amplified a PCR product of the expected size. However, three of them were either monomorphic or did not yield a PCR product in the three final multiplexes using the labeled forward primers, and were consequently not used for further analyses. Hence, in combination with the eight previously developed markers (Baumgartner et al., 2009; Prospero et al., 2010), the samples were genotyped at 17 polymorphic SSR loci scattered all over the genome (Supplementary Figure S1.1, Appendix 1). All SSR loci revealed a considerable level of polymorphism with a frequency of the most common allele lower than 95%. Missing data for both sets of markers were observed in <5% of the samples across loci and populations, except for the SSR locus AC18 which contained 15% missing data in the Carpathian and almost 40% in the Alpine populations. Multilocus genotypes with missing data in loci other than AC18 were excluded from further analyses.
In addition to the high percentage of missing data, SSR locus AC18 also revealed a significant deficiency of heterozygotes and a statistically consistent deviation from Hardy–Weinberg equilibrium in all four subpopulations (Supplementary Table S2.1, Appendix 2). This is strong evidence for the presence of null alleles. However, as null allele frequencies at this locus differ between Carpathian and Alpine populations and thus can be used for the STRUCTURE analysis (RECESSIVEALLELES settings), we kept it for further tests.
The linkage disequilibrium test showed that a significant correlation between allele frequencies among all subpopulations was only present at SNPs which are located in the same gene. Thus, for population structure analyses, only one random SNP locus per gene was considered, resulting in a total of 24 SNPs. Non-random association of allele frequencies was also observed for other pairs of SNP and SSR loci in specific subpopulations, but the statistical support was not consistent across loci and subpopulations (Supplementary Table S2.2, Appendix 2). Noteworthy, these pairwise correlated loci were located in different scaffolds across the genome (Supplementary Figure S1.1, Appendix 1). The two multilocus estimators of non-random association between alleles (IA and rbarD) were low across all subpopulations and markers (Table 1). However, in the two Carpathian subpopulations, non-random associations in SSR loci were supported by significant P-values.
BAYESCAN revealed no FST outliers in both SSRs and SNPs (Supplementary Figures S3.1B and S3.2B, Appendix 3), suggesting that all loci were selectively neutral in the studied populations and subpopulations. In contrast, ARLEQUIN showed locus-specific deviation of FST at the SSR locus AC31 (95% confidence interval) when analyzing the Carpathian subpopulations separately (Supplementary Figure S3.3A, Appendix 3), which might indicate that natural selection acted on this locus in Carpathian A. cepistipes. Similarly, SNP loci FG848_7 and FG894_7 were identified as FST outliers (99% confidence interval) with ARLEQUIN in the two Alpine subpopulations (Supplementary Figure S3.6A, Appendix 3). In the overall analysis, assuming a finite island migration scenario between the Carpathian and Alpine populations, ARLEQUIN revealed no SSR locus being under selection, whereas the two SNP loci MS481_16 and FG730_11 showed evidence of being under purifying selection (Supplementary Figure S3.2A, Appendix 3). As these analyses revealed no consistent FST outliers among statistical approaches and population sets, all loci were considered as neutral and kept for further analysis.
Genetic diversity
Among the 407 isolates genotyped with 17 SSRs, 359 exhibited a unique combination of alleles, whereas only 278 unique SNP MLGs were detected (Table 1). All 17 SSR loci were polymorphic in the investigated A. cepistipes populations and harbored a total of 135 alleles. Eighteen alleles were specific for the Carpathian population, whereas only 11 private alleles were detected in the Alpine population. Within the Carpathian population, each subpopulation harbored five private alleles. The two Alpine subpopulations exhibited five (North) and three (South) private alleles. Mean allelic richness (Ar) across SSR loci was similar in all four subpopulations (Table 2), but varied considerably among loci (Supplementary Table S2.1, Appendix 2). Two of the 31 SNP loci were polymorphic in only the Carpathian population (Supplementary Table S2.1, Appendix 2). Just as for Ar, evenness (E) of alleles and expected heterozygosity (Hexp) across SSR and SNP loci showed only little variation among subpopulations (Table 2), but high variation among loci (Supplementary Table S2.1, Appendix 2). Within subpopulations, SSR loci exhibited higher Hexp than SNP loci (Table 2).
Population structure
Pairwise FST values between subpopulations were low for both types of molecular markers (across SSR loci: from −0.01 to 0.08; across SNP loci: from −0.01 to 0.17), and even between the two substantially distant (>1000 km apart) Alpine and Carpathian populations (SSR-FST=0.025, SNP-FST=0.026). Despite the generally low but statistically significant (P<0.05) values of FST, those computed between geographically distant subpopulations, for example, Alpine South and Carpathian Beech were from 2 (SNPs) to 10 (SSRs) times higher than those between subpopulations within a mountain range (Table 3). An extremely low and statistically non-significant FST value was obtained with SNP markers between the two subpopulations of the Carpathians (Beech and Mixed/conifer) which were sampled at small spatial scales. Similarly, SSR markers revealed a non-significant FST value between the two Alpine subpopulations which were randomly sampled at a large spatial scale (Table 3).
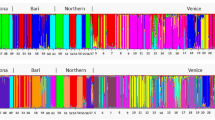
In the overall STRUCTURE analysis using all four subpopulations, SSRs revealed a larger number of genetic clusters than SNPs (Figure 2). For the SSR data, the log-likelihood increased constantly up to 20 clusters (Figure 2a). However, the s.d.’s of the log-likelihood values increased simultaneously and became particularly high for some K⩾5, like K=9 and K=12. Up to K=20, increasing K led to individuals assigned to new clusters with high probability and revealed a complex structure within the small-scaled Carpathian subpopulations (Figure 2b, Supplementary Figure S4.1, Appendix 4). For the SNP data, the log-likelihood was highest at K=2 and high s.d.’s of log-likelihood values suggested unstable results for K>3 (Figure 2a). Unlike in the SSR data set, increasing K>3 did not assign fungal MLGs to new clusters and did not suggest a more complex genetic structure within any of the studied subpopulations. However, K=3 supports the existence of two large-scaled Alpine subpopulations and one Carpathian population (Figure 2b, Supplementary Figure S4.2, Appendix 4). Additional STRUCTURE analyses using only the two Alpine subpopulations (Supplementary Figure S4.4, Appendix 4) showed the highest log-likelihood at K=2 and confirmed the assignment pattern. Considering the two methods of K determination described above (highest log-likelihood and sequential cluster assignment of the MLGs) and in order to avoid an overestimation of the number of genetic clusters in the studied populations, we assumed K=4 as reasonable to describe the genetic structure with the SSR markers and K=3 as the most likely number of genetic clusters with the SNP markers.
STRUCTURE results using 17 SSR loci and 24 SNP loci in four geographic subpopulations of Armillaria cepistipes. (a) Scatterplots with mean log-likelihood values (±s.d.) for different numbers of clusters (K). (b) Barplots representing the average estimated membership probability (y axis) of an individual to belong to a specific cluster (indicated by specific color).
The four genetic clusters identified using SSRs split the 359 MLGs according to their geographic origin (Figure 2b, SSRs, K=4). All MLGs of the two Alpine subpopulations belonged to the same (green) cluster, whereas those from the two Carpathian subpopulations were mainly attributed to one (blue) of the other three clusters. However, in these two latter subpopulations a significant mixture of MLGs that belonged to the remaining two clusters (yellow and orange) was also observed. The STRUCTURE analyses revealed an almost complete absence of MLGs with admixed genetic origin in the large and randomly sampled population from the Alps. In contrast, such admixed MLGs were frequent in the two subpopulations of the Carpathians sampled across a smaller spatial scale, especially in the mixed and conifer forests. Most admixed MLGs from the orange cluster were present in this specific subpopulation (Figure 2b, SSRs, K=4).
The STRUCTURE analysis with the SNP data for K=3 (Figure 2b, SNPs, K=3) revealed that the Carpathian and Alpine populations were clearly separated, with the first population including mainly MLGs from one cluster (green, membership probability of 60–80%) and the latter from two clusters (blue and yellow). Noteworthy, the pattern of subdivision within populations was the opposite as the one observed with SSRs. The small-scaled subpopulation of the Carpathian Mountains was homogeneous, whereas in the large Alpine population the two subpopulations (North and South) were clearly differentiated (Figure 2b, SNPs, K=3). This signal of differentiation between the two Alpine subpopulations substantially disappeared when the five SNPs (loci: MS481_16, FG730_11, FG848_7, FG894_7 and FG524_2) that showed deviation from neutral patterns (Supplementary Figures S3.2 and Supplementary Figures S3.6, Appendix 3) were excluded from the cluster analyses (Supplementary Figure S4.3, Appendix 4).
Cluster assignments with both types of loci were also examined with a discriminant analysis of PCs (DAPC, Figure 3). Based on lowest root mean squared error and highest mean of successful reassignments with 1000 replicates (cross-validation), 90 (of 117) and 20 (of 24) computed PCs were retained in the discriminant analysis using SSRs and SNPs, respectively. Three discriminant functions were built for each analysis. In both types of markers, no strong association was detected between MLG assignments and their geographic origin. The individual posterior probabilities of assignment to a pre-defined geographic group were low for both the SSR and SNP data in all studied subpopulations. However, the proportion of MLGs successfully assigned (with posterior probability >95%) to the pre-defined geographic subpopulation differed between the genetic markers (SSRs 35% of studied MLGs; SNPs 0.36%, that is, only one MLG).
Discriminant analysis of principle components (DAPC) computed with 17 SSRs and 24 SNPs in four subpopulations of Armillaria cepistipes. Scatterplots represent the distribution of individuals (symbols) along the first two linear discriminants that explain 74% and 15% of the PCs’ variances using SSRs (left) and 71% and 22% using SNPs (right). The cross-validated number of the PCs used for the discriminant analysis is shown in dark color in the bar plots on the top right of each scatterplot.
Overall, the DAPC clustering agreed with the one of the STRUCTURE analyses (Figures 2 and 3). In both SSRs and SNPs, the first discriminant separated the MLGs of the Carpathians and the Alps (Figure 3). With the SSR data, the two subpopulations of the Carpathians were further discriminated along the second axis, whereas the individuals from the two Alpine subpopulations largely overlapped (Figure 3). The opposite situation was observed in the SNP data, where the least overlap was observed between the two Alpine subpopulations. One noteworthy difference between the STRUCTURE and DAPC clustering could be observed with the SSR data (Figures 2 and 3). Although STRUCTURE revealed a complex structure within the Carpathian subpopulations, the DAPC identified prominent differences between Beech and Mixed/conifer forests.
Discussion
In this study, we aimed to compare the utility of SNP and SSR markers for investigating the neutral population genetic structure of the basidiomycete A. cepistipes at different spatial scales. Analyzing the population structure of such an organism implies also addressing several other issues, such as the contribution of different reproduction modes to its spread at large and small geographic scales, the connectivity among populations in a heterogeneous environment and their demographic history. Our analysis revealed differences in the information that the two types of markers give about genetic structure within large and small geographic scales based on the example of two populations from mountain forests in Europe. Noteworthy, SSRs provided a higher resolution at a smaller geographic scale under a systematic sampling (Carpathian population), whereas SNPs were able to differentiate the two subpopulations which were randomly sampled across a large area in the Alps.
Both types of markers revealed the presence of repeatedly occurring genotypes in the investigated populations. However, a higher number of MLGs was detected when using the 17 SSRs (359 MLGs in 407 isolates) than when using the 24 SNPs (278 MLGs). This result confirms that multi-allelic SSR markers have a higher discrimination power than bi-allelic SNP markers (Guichoux et al., 2011). High levels of genotypic diversity are generally expected in populations of fungi that mainly reproduce sexually. However, previous population genetic studies conducted in natural and managed forests in Europe showed that this is not always the case in Armillaria species (Prospero et al., 2008). Because of the spread via vegetative rhizomorphs, Armillaria species may produce large genets that occupy a forest area of several hectares (Bendel et al., 2006). Thus, the presence of such genets can reduce genotypic diversity. Moreover, mating of closely related haploids produced by spatially distributed clones via basidiospores during sexual reproduction will influence population structure and consequently change statistical estimators, (for example, IA and rbarD) even after the clone-correction procedure.
Significant differences between SNPs and SSRs were observed with respect to heterozygosity (paired t-tests, n=4, P<0.001), but not to FST (paired t-test, n=6, P=0.30). As expected due to their multi-allelic nature and usually higher level of polymorphism, SSR loci exhibited a significantly higher heterozygosity than bi-allelic SNP loci. However, locus-specific values showed a wide range, possibly because of uneven allelic richness. Previous studies argued that both high and low numbers of alleles at SSR loci may affect the accuracy of heterozygosity estimates and consequently of population-specific fixation indices (Wang, 2015; Fischer et al., 2017). In our study, SSRs were selected with an emphasis on different nucleotide number and GC content in the tandem repeats. Therefore, the ascertainment bias due to the selection of genomic fragments with exclusively high levels of polymorphism should be minor. For this reason, allelic richness and heterozygosity estimators vary considerably among loci.
In Armillaria populations, heterozygosity may also be strongly influenced by the mixed mating system. Clonal reproduction by rhizomorphs maintains heterozygosity (De Meeûs et al., 2007), whereas sexual reproduction increases it. In Armillaria species, spore release is intense but spore dispersal seems to be spatially limited (Travadon et al., 2012; Dutech et al., 2017). This may lead to inbreeding processes like mating between closely related haplotypes and plasmogamy of haploid spores (or mycelium) with their diploid parents, which may both reduce heterozygosity. As inbreeding and outbreeding processes can occur simultaneously in Armillaria populations, heterozygosity may not accurately explain demographic processes (for example, gene flow between populations or a Wahlund effect due to population subdivision) in these fungi, regardless whether SNPs or SSRs are used. Nonetheless, at large and small scales, we observed a heterozygote deficit at most loci for both types of genetic markers, suggesting a predominance of inbreeding processes. However, the high abundance of rhizomorphs (Tsykun et al., 2012) and presence of repeated MLGs within different localities, also the low but significant indices of multilocus association (IA and rbarD) in the Carpathians suggest that clonal reproduction also might influence demographic processes in this population. Therefore, we can assume that this population is driven by inbreeding processes along with clonal spreading via rhizomorphs. However, long-distance spore dispersal cannot be excluded and is indirectly supported in our study by the low number of private alleles, the lack of a strong structure between subpopulations within mountain ranges (regardless of sampling design or spatial scale) and the low differentiation between the geographically distant Carpathian and Alpine populations (see below).
Pairwise FST values between the studied fungal populations and subpopulations, even between geographically distant ones (like Alpine vs Carpathian), were low (0.001–0.036) with both types of markers. It is known that FST is very sensitive to the level of within-population variation, resulting in suspiciously low values in SSR studies and a consequent underestimation of the level of population divergence (Brumfield et al., 2003). However, low pairwise FST values in Armillaria (Giraud et al., 2008; Baumgartner et al., 2010; Heinzelmann et al., 2012), as well as in other fungi (Giraud et al., 2008), are rather the rule than the exception. This suggests low overall population differentiation due to extensive gene flow among populations. Although such high gene flow may be present between the two subpopulations of the rather continuous Carpathian primeval forests, it is less realistic between the two Alpine subpopulations and between the Alpine and Carpathian populations, which are separated by the Alps and a large geographic distance, respectively. An alternative explanation for the low FST values may be a common glacial refugium of the A. cepistipes populations, possibly coupled with a relatively slow population divergence and homoplasy events. Recently, several authors (for example, Jost, 2008; Meirmans and Hedrick, 2011) have criticized the use of FST as a measure of population differentiation. Since this estimator seems to be negatively correlated with the number of alleles per locus, FST tends to have values towards zero in populations with high allelic richness and thus underestimates the actual divergence between populations (Jost, 2008). In our study, low FST values were not only detected with the multi-allelic SSR markers, but also with the bi-allelic SNPs. In a comparative study by Fischer et al. (2017), substantially higher FST values were obtained with a limited number of SSRs than with genome-wide SNPs. The authors emphasized that pairwise FST calculated from SSRs must be used with caution. In particular, one should not rely on absolute values because it can reflect rather the highly polymorphic nature of the markers than a real whole-genome differentiation of populations. In our study, we used a limited number of SNPs, which were selected because they exhibited a sufficient level of polymorphism. Thus, this specific set of SNPs might induce an ascertainment bias and show a higher population differentiation than genome-wide SNPs that contain many low-frequency alleles. Regardless of the overall low absolute FST values, for both types of markers, the genetic differentiation between distant populations (Carpathian vs Alpine) was substantially higher than the one between subpopulations of the same mountain region. Using SNPs, the highest differentiation was observed between the most distant subpopulations that are separated by a high mountain range, that is, between both Carpathian subpopulations and the subpopulation of the South Alps. In contrast, with the SSR data, the FST value for the subpopulations sampled at a small spatial scale, that is, Beech and Mixed/conifer subpopulations of Carpathians, was higher (and significantly different from zero) than the one from the SNP data.
Overall, the two clustering methods (DAPC and STRUCTURE) used for investigating population genetic structure produced consistent results. The geographically distant populations (that is, Carpathian and Alpine) showed a clear separation with both types of markers. SSRs and SNPs, however, gave different signals within the two populations sampled at different spatial scales. SSRs exhibited a considerable admixture of clusters in the two geographically close and systematically sampled subpopulations of the Carpathian forests in the STRUCTURE analysis, suggesting the same ancestral origin and/or possible gene flow among populations. The DAPC analysis, however, was able to define genetic components that differ between the Carpathian subpopulations, suggesting a weak subdivision. Because in this region the landscape barriers for spore dispersal are relatively weak (for example, low mountain relief and small distance between the studied forests), genetic exchange between these subpopulations is a realistic scenario. However, the clustering with SSRs showed also that fungal populations sampled within a small-scaled area might have a complex genetic structure. The mainly monocultural beech forests of the Carpathians seem to harbor a more homogenous A. cepistipes population which were resolved into only two genetic clusters in the STRUCTURE analysis, whereas the mixed and pure conifer forests contain a more diverse A. cepistipes population (three clusters). This result, however, is different using SNPs with both DAPC and STRUCTURE, evidencing only one single genetic cluster across both spatially close subpopulations of the Carpathians. It is important to note that these SNPs were initially selected from housekeeping genes present in the genomes of five fungal species other than Armillaria (Dutech et al., 2016). Therefore, SNPs in such conserved genes may rather reflect long-term divergence among populations than recent processes. Apparently, the two Carpathian subpopulations have not yet diverged enough to reveal nucleotide differences in the genes considered.
In contrast to using SSRs, the two large-scaled subpopulations that are separated by a high mountain range (North and South of Alpine population) were assigned to two different clusters using SNPs. The two SNP loci that were mainly responsible for this discrimination were also significant outliers in ARLEQUIN (but not in BAYESCAN). This suggests that the Alpine mountain range left its traces on the long-term divergence of the northern and southern A. cepistipes subpopulations. The presence of only one genetic cluster in the large-scaled Alpine population based on SSRs might be at least partially due to the particular sampling design applied. The two Alpine subpopulations mainly share the same alleles at all 17 SSR loci. Thus, a random sampling of distant individuals at a large spatial scale may not accurately reveal local population allele frequencies to infer subpopulation structure with SSRs. In contrast, scattered sampling at large scale did not affect the discrimination power of SNPs. This is most likely because differences among geographically distant populations in SNP loci were fixed along an evolutionary time scale, making it easier to detect population-specific allele frequencies even with a scattered random sampling. Our results are in agreement with those of a study on the global migration patterns of the pathogenic crop fungus Mycosphaerella graminicola (Banke and McDonald, 2005). The authors found that SSRs were sensitive to detect recent (50–150 years) migration events between North and South American populations, whereas protein-coding loci were not. Based on these and on our results, we conclude that SSRs have a higher resolution for genetically and spatially close populations (as in the Carpathian subpopulations) with extensive gene flow. In contrast, SNPs in housekeeping genes seem to be more appropriate for phylogeographic large-scale studies (as in the Alpine subpopulations). However, this conclusion should be treated with caution, because our study design does not allow disentangling the possible confounding effects of sampling scale and population-specific demography on marker performance.
In summary, the present study revealed differences on inferences of population genetic structure of the fungus Armillaria cepistipes at different spatial scales when using two different marker types (SSRs and SNPs). SSRs were found to be better suited for detecting structure in populations at a small spatial scale with a systematic and continuous sampling design (as shown in the example of the Carpathian population). The patterns observed in the SNP markers rather reflect ancient divergence of distant and naturally separated populations, being less sensitive to sampling design (as shown in the example of the Alpine population). A full factorial sampling design and a higher genomic resolution would help to strengthen the reliability of the obtained results. Nevertheless, both marker types were suitable for detecting the weak genetic structure of the two fungal populations considered.
Data archiving
Genotype data have been submitted to Dryad: http://dx.doi.org/10.5061/dryad.t29f8.
References
Agapow P-M, Burt A . (2001). Indices of multilocus linkage disequilibrium. Mol Ecol Notes 1: 101–102.
Banke S, McDonald B . (2005). Migration patterns among global populations of the pathogenic fungus Mycosphaerella graminicola. Mol Ecol 14: 1881–1896.
Baumgartner K, Coetzee MPA, Hoffmeister D . (2011). Secrets of the subterranean pathosystem of Armillaria. Mol Plant Pathol 12: 515–534.
Baumgartner K, Grubisha LC, Fujiyoshi P, Garbelotto M, Bergemann SE . (2009). Microsatellite markers for the diploid basidiomycete fungus Armillaria mellea. Mol Ecol Resour 9: 943–946.
Baumgartner K, Travadon R, Bruhn J, Bergemann SE . (2010). Contrasting patterns of genetic diversity and population structure of Armillaria mellea sensu stricto in the Eastern and Western United States. Phytopathology 100: 708–718.
Bendel M, Kienast F, Rigling D . (2006). Genetic population structure of three Armillaria species at the landscape scale: a case study from Swiss Pinus mugo forests. Mycol Res 110: 705–712.
Boutin-Ganache I, Raposo M, Raymond M, Deschepper CF . (2001). M13-tailed primers improve the readability and usability of microsatellite analyses performed with two different allele-sizing methods. Biotechniques 31: 28.
Brumfield RT, Beerli P, Nickerson DA, Edwards SV . (2003). The utility of single nucleotide polymorphisms in inferences of population history. Trends Ecol Evol 18: 249–256.
Carvalho DB, Smith M, Anderson J . (1995). Genetic exchange between diploid and haploid mycelia of Armillaria gallica. Mycol Res 99: 641–647.
Coates BS, Sumerford DV, Miller NJ, Kim KS, Sappington TW, Siegfried BD et al. (2009). Comparative performance of single nucleotide polymorphism and microsatellite markers for population genetic analysis. J Hered 100: 556–564.
De Meeûs T, McCoy KD, Prugnolle F, Chevillon C, Durand P, Hurtrez-Bousses S et al. (2007). Population genetics and molecular epidemiology or how to “débusquer la bête”. Infect Genet Evol 7: 308–332.
Dutech C, Labbé F, Capdevielle X, Lung-Escarmant B . (2017). Genetic analysis reveals efficient sexual spore dispersal at a fine spatial scale in Armillaria ostoyae, the causal agent of root-rot disease in conifers. Fungal Biol 121: 550–560.
Dutech C, Prospero S, Heinzelmann R, Fabreguettes O, Feau N . (2016). Rapid identification of polymorphic sequences in non-model fungal species: the PHYLORPH method tested in Armillaria species. Forest Pathol 46: 298–308.
Earl DA, vonHoldt BM . (2011). STRUCTURE HARVESTER: a website and program for visualizing STRUCTURE output and implementing the Evanno method. Conserv Genet Resour 4: 359–361.
Estoup A, Jarne P, Cornuet JM . (2002). Homoplasy and mutation model at microsatellite loci and their consequences for population genetics analysis. Mol Ecol 11: 1591–1604.
Excoffier L, Hofer T, Foll M . (2009). Detecting loci under selection in a hierarchically structured population. Heredity 103: 285–298.
Fischer MC, Rellstab C, Leuzinger M, Roumet M, Gugerli F, Shimizu KK et al. (2017). Estimating genomic diversity and population differentiation – an empirical comparison of microsatellite and SNP variation in Arabidopsis halleri. BMC Genom 18: 69.
Foll M, Gaggiotti O . (2008). A genome-scan method to identify selected loci appropriate for both dominant and codominant markers: a bayesian perspective. Genetics 180: 977–993.
Giraud T, Enjalbert J, Fournier E, Delmotte F, Dutech C . (2008). Population genetics of fungal diseases of plants. Parasite 15: 449–454.
Goudet J . (2002). FSTAT v 2.9.3.2, A Program to Estimate and Test Gene Diversities and Fixation Indices. https://www2.unil.ch/popgen/softwares/fstat.htm.
Guichoux E, Lagache L, Wagner S, Chaumeil P, Léger P, Lepais O et al. (2011). Current trends in microsatellite genotyping. Mol Ecol Resour 11: 591–611.
Heinzelmann R, Rigling D, Prospero S . (2012). Population genetics of the wood-rotting basidiomycete Armillaria cepistipes in a fragmented forest landscape. Fungal Biol 116: 985–994.
Jakobsson M, Rosenberg NA . (2007). CLUMPP: a cluster matching and permutation program for dealing with label switching and multimodality in analysis of population structure. Bioinformatics 23: 1801–1806.
Jombart T, Devillard S, Balloux F . (2010). Discriminant analysis of principal components: a new method for the analysis of genetically structured populations. BMC Genet 11: 94.
Jost L . (2008). GST and its relatives do not measure differentiation. Mol Ecol 17: 4015–4026.
Kaiser SA, Taylor SA, Chen N, Sillett TS, Bondra ER, Webster MS . (2016). A comparative assessment of SNP and microsatellite markers for assigning parentage in a socially monogamous bird. Mol Ecol Resour 17: 183–193.
Kamvar ZN, Tabima JF, Grunwald NJ . (2014). Poppr: an R package for genetic analysis of populations with clonal, partially clonal, and/or sexual reproduction. PeerJ 2: e281.
Kim S, Plagnol V, Hu TT, Toomajian C, Clark RM, Ossowski S et al. (2007). Recombination and linkage disequilibrium in Arabidopsis thaliana. Nat Genet 39: 1151–1155.
Li Y-C, Korol AB, Fahima T, Beiles A, Nevo E . (2002). Microsatellites: genomic distribution, putative functions and mutational mechanisms: a review. Mol Ecol 11: 2453–2465.
Ljungqvist M, Åkesson M, Hansson B . (2010). Do microsatellites reflect genome‐wide genetic diversity in natural populations? A comment on. Mol Ecol 19: 851–855.
Meirmans PG, Hedrick PW . (2011). Assessing population structure: FST and related measures. Mol Ecol Resour 11: 5–18.
Münsterkötter M, Walter M, Güldener U, Sipos G . (2015) 28th Fungal Genetics Conference, Vol. (Suppl): Abstract. Fungal Genetics Reports: Pacific Grove, CA, pp 237.
Nieuwenhuis BPS, James TY . (2016). The frequency of sex in fungi. Philos Trans R Soc B Biol Sci 371: 1–12.
Okonechnikov K, Golosova O, Fursov M . (2012). Unipro UGENE: a unified bioinformatics toolkit. Bioinformatics 28: 1166–1167.
Pritchard JK, Stephens M, Donnelly P . (2000). Inference of population structure using multilocus genotype data. Genetics 155: 945–959.
Prospero S, Jung E, Tsykun T, Rigling D . (2010). Eight microsatellite markers for Armillaria cepistipes and their transferability to other Armillaria species. Eur J Plant Pathol 127: 165–170.
Prospero S, Lung-Escarmant B, Dutech C . (2008). Genetic structure of an expanding Armillaria root rot fungus (Armillaria ostoyae) population in a managed pine forest in southwestern France. Mol Ecol 17: 3366–3378.
Rosenberg NA . (2004). distruct: a program for the graphical display of population structure. Mol Ecol Notes 4: 137–138.
Rousset F . (2008). genepop’007: a complete re-implementation of the genepop software for Windows and Linux. Mol Ecol Resour 8: 103–106.
Travadon R, Smith ME, Fujiyoshi P, Douhan GW, Rizzo DM, Baumgartner K . (2012). Inferring dispersal patterns of the generalist root fungus Armillaria mellea. New Phytol 193: 959–969.
Tsykun T, Rigling D, Nikolaychuk V, Prospero S . (2012). Diversity and ecology of Armillaria species in virgin forests in the Ukrainian Carpathians. Mycol Prog 11: 403–414.
Väli Ü, Einarsson A, Waits L, Ellegren H . (2008). To what extent do microsatellite markers reflect genome‐wide genetic diversity in natural populations? Mol Ecol 17: 3808–3817.
Wang J . (2015). Does GST underestimate genetic differentiation from marker data? Mol Ecol 24: 3546–3558.
Wang J, Fernández-Pavía SP, Larsen MM, Garay-Serrano E, Gregorio-Cipriano R, Rodríguez-Alvarado G et al. (2017). High levels of diversity and population structure in the potato late blight pathogen at the Mexico centre of origin. Mol Ecol 26: 1091–1107.
Weir BS, Cockerham CC . (1984). Estimating F-statistics for the analysis of population structure. Evolution 38: 1358–1370.
Zhao Z, Fu Y-X, Hewett-Emmett D, Boerwinkle E . (2003). Investigating single nucleotide polymorphism (SNP) density in the human genome and its implications for molecular evolution. Gene 312: 207–213.
Acknowledgements
We are grateful to E. Guichoux and A. Delcamp (Genome Transcriptome Facility of INRA, Bordeaux), E. Jung (Phytopathology, WSL) and the team of the Genetic Diversity Center (GDC, ETH Zürich) for laboratory assistance and expert help. We also thank R. Holderegger for useful discussions while analyzing and interpreting results, and three anonymous referees for the critical comments on the manuscript. This work was financially supported by the Swiss Federal Research Institute WSL, by the program ‘Trees4Future’, a project co-funded by the European Union Seventh Framework FP7 under grant agreement no. 284181, and by the Swiss Government Excellence Scholarships for Foreign Scholars and Artists for the Academic Year 2014–2015 of the State Secretariat for Education, Research and Innovation (SERI) to TT. The A. cepistipes genome project was founded by the European Union in the frame of the Széchenyi 2020 Programme (GINOP-2.3.2-15-2016-00052) and by the WSL to GS.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies this paper on Heredity website
Rights and permissions
About this article
Cite this article
Tsykun, T., Rellstab, C., Dutech, C. et al. Comparative assessment of SSR and SNP markers for inferring the population genetic structure of the common fungus Armillaria cepistipes. Heredity 119, 371–380 (2017). https://doi.org/10.1038/hdy.2017.48
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/hdy.2017.48
This article is cited by
-
WAASB-based stability analysis and validation of sources resistant to Plasmopara halstedii race-100 from the sunflower working germplasm for the semiarid regions of India
Genetic Resources and Crop Evolution (2024)
-
Genetic diversity, population structure and selection signatures in Enset (Ensete ventricosum, (Welw.) Cheesman), an underutilized and key food security crop in Ethiopia
Genetic Resources and Crop Evolution (2024)
-
Genotypic diversity and population structure of the apricot landraces of the Campania region (Southern Italy) based on fluorescent SSRs
Genetic Resources and Crop Evolution (2023)
-
Global invasion history of the emerging plant pathogen Phytophthora multivora
BMC Genomics (2022)
-
In silico genome-wide discovery and characterization of SSRs and SNPs in powdery mildew disease resistant and susceptible cultivated and wild Helianthus species
Vegetos (2022)