Introduction

Understanding the processes that give rise to population genetic variation is central to theory on local adaptation (Lenormand, 2002), speciation (Coyne and Orr, 2004) and geographic range limits (Bridle and Vines, 2007). Such knowledge can also be valuable for prioritizing vulnerable populations for conservation (Lesica and Allendorf, 1995). For example, populations with low genetic diversity may lack the evolutionary potential needed to adapt to different or changing environments (Hoffmann and Sgrò, 2011); they may also be more prone to inbreeding depression (O’Grady et al., 2006; but see Bijlsma et al., 1999) and less able to withstand ecological perturbations (Hughes et al., 2008).

The central–marginal hypothesis (CMH) provides a spatial perspective for the processes that shape population genetic variation, predicting that populations at the periphery of a species’ range will have lower genetic diversity and will be more genetically differentiated from one another when compared with central populations (Antonovics, 1976; Brussard, 1984; Eckert et al., 2008). These predictions are based on the observation that peripheral populations often occur in patchy and marginal habitat (abundant center model; Sagarin and Gaines, 2002), which could (1) exacerbate genetic drift (because of low population density) and (2) reduce gene flow (because of diminished habitat connectivity; see Supplementary Figure S1 for a schematic diagram). Along the periphery of a species’ range, immigrants can also arrive from fewer directions, which has the potential to further reduce the amount of incoming gene flow (Schwartz et al., 2003). In a meta-analysis that included a range of plant and animal taxa, Eckert et al. (2008) found that most studies with data suitable for testing the CMH documented lower genetic diversity (64% of studies) and greater genetic differentiation (70% of studies) in peripheral versus central populations, supporting the CMH. Most of the studies, however, focused on geographically widespread species, and hence the degree to which the CMH applies to species distributed across smaller spatial scales is unclear.

The CMH may apply to single populations or narrowly distributed species because the processes that generate and maintain spatial variation in genetic diversity and differentiation operate at multiple spatial scales. Genetic structure created by spatial limitations to gene flow (for example, isolation by distance, isolation by environment, isolation by fragmentation) is commonly observed in natural populations (Sexton et al., 2014) and, for some species, is detectable at fine spatial scales (see, for example, Carlsson et al., 1999; Porlier et al., 2012; Langin et al., 2015). Therefore, certain segments of the population may experience lower levels of gene flow than others. The strength of genetic drift could also vary spatially, especially in populations that exhibit fine-scale genetic structure, because local variation in the quality and quantity of habitat influences population density (Wiens, 1976). Taken together, these findings suggest that the CMH could apply to single, continuously distributed populations, but few studies have tested the CMH at fine spatial scales (although see Pouget et al., 2013).

Here we examine spatial variation in genetic diversity and differentiation in the Island Scrub-Jay (Aphelocoma insularis), a bird of conservation concern that is only found on one small island (250 km2 Santa Cruz Island) 37 km from the mainland of southern California, USA. This species provides a unique opportunity to test predictions of the CMH at a fine spatial scale because it consists of a single, bounded population (Langin et al., 2015) with no evidence of gene flow with mainland Aphelocoma (McCormack et al., 2011). Furthermore, despite its narrow geographic range, the species exhibits many properties that are often observed at a broader spatial scale in widely distributed taxa: the density of Island Scrub-Jays is highest toward the center of the island (see Supplementary Figure S2) and the species exhibits spatial genetic structuring across its range, driven mostly by highly localized dispersal resulting in a pattern of isolation by distance (Langin et al., 2015). Previous work on this species has also documented microgeographic adaptation in bill morphology to pine and oak habitats (Langin et al., 2015).

We hypothesized that, given localized dispersal and reduced population densities on the periphery of the island, the genetic characteristics of this population would vary spatially in accordance with the CMH. We predicted that individuals in peripheral portions of the island would exhibit (1) lower individual-level genetic diversity (higher homozygosity) and (2) greater genetic differentiation among neighboring individuals (stronger localized isolation by distance) as compared with more central portions of the island. We note that although Langin et al. (2015) documented isolation by distance within the Island Scrub-Jay population as a whole, previous work has not tested whether the strength of isolation by distance is greater on the island periphery than the center, the basis of our second prediction. We tested these predictions empirically using data from 12 putatively neutral loci that were genotyped in a quarter of the Island Scrub-Jay population (using data previously published in Langin et al., 2015). We also used simulations to examine how restricted dispersal, spatial variation in density and total population size contributed to observed patterns of genetic diversity in the Island Scrub-Jay population. Our methodology differs somewhat from the typical approach used to test the CMH in that we compared genetic diversity and differentiation within and among individuals, rather than within and among populations. Such an approach was taken because previous spatial genetic analyses revealed continuous genetic structure within Island Scrub-Jays, with no sharp genetic breaks indicative of the presence of multiple populations (Langin et al., 2015).

Materials and methods

Study system

The global population of Island Scrub-Jays consists of <3000 individuals (Sillett et al., 2012) found on Santa Cruz Island, the largest of the California Channel Islands. Most Island Scrub-Jays live and breed in oak (Quercus spp.) chaparral, but a subset of the population occurs in stands of Bishop Pine (Pinus muricata) forest. The habitat available to Island Scrub-Jays has a patchy distribution, both because of topographic and environmental complexity and also because of the historical effects of grazing by non-native ungulates (Morrison, 2007). Gene flow in this system is not impeded by habitat fragmentation or transitions between habitat types (although there is evidence for a subtle reduction in gene flow across one boundary between oak and pine habitats); instead, the primary driver of spatial genetic structure within the species is a gradual pattern of isolation by distance (Langin et al., 2015). This genetic pattern is likely due to limited dispersal. Island Scrub-Jays have not been observed establishing a breeding territory >4 km from their natal territory (Langin et al., 2015).

Sample collection

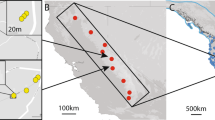
We collected blood samples from 544 individually marked Island Scrub-Jays from 2009 to 2011 (Figure 1); see Langin et al. (2015) for further details. Geographic coordinates were recorded with a GPS (Global Positioning System) unit for every sampling location. Sampling occurred in oak and pine habitats and was not evenly distributed because (1) the island is rugged and has a limited road network, so some regions were difficult to access (in some cases we used helicopter transportation) and (2) capture efforts were disproportionately focused on three long-term demography plots (see Caldwell et al., 2013). All work was approved by animal care and use committees at Colorado State University and the Smithsonian Institution.

Figure 1
figure 1

Map of Santa Cruz Island, California, USA, showing the locations where genetic samples were collected from Island Scrub-Jays (n=544). The island is shaded a darker color in areas that have woody vegetation, and hence habitat suitable for Island Scrub-Jays. White circles are sample locations and the white cross represents the geographic center of the island.

Full size image

Microsatellite genotyping

Microsatellite data were previously analyzed for a different purpose and published in Langin et al. (2015). See that publication for a full description of methods, including analyses testing for genotyping errors and departures from neutrality and independent assortment. In brief, DNA was extracted and all samples were genotyped at 12 polymorphic microsatellite loci (mean allelic diversity was 15 alleles per locus). If individuals had missing genotype data, they were regenotyped; nevertheless, a subset of individuals still had missing data in the final data set (10 individuals had data missing for one locus, and one individual had data missing for two loci).

Analyses

Spatial variation in genetic diversity

We measured individual-level genetic diversity in Island Scrub-Jays using the index ‘homozygozity by loci’ (HL; Aparicio et al., 2006), which varies between zero (all loci heterozygous) and one (all loci homozygous). The method weights loci based on their allelic diversity and evenness, such that a homozygous state results in the greatest increase in HL when it occurs at the locus with the highest expected heterozygosity. HL values were calculated using the R package Rhh (Alho et al., 2010). The HL calculation method requires complete genotype data, so individuals with data missing for some loci (n=11) were excluded from analyses involving HL.

To test the first prediction of the CMH, we ran a spatial error model (implemented in the R package spdep) to test for a relationship between HL and the distance each individual was captured relative to the geographic center of Santa Cruz Island (represented by the island’s centroid: 34° 00' 50.3'N, 119° 44' 42.5'W). We chose to use a spatial error model because we detected spatial autocorrelation in the residuals of a simple linear model. The distance-to-island-center variable was right skewed (relatively few individuals were sampled far from the island center), and hence a log-transformation was applied. Inverse distance weights were used to model spatial autocorrelation. We assessed the strength of evidence for the relationship between HL and distance-to-island-center using a log-likelihood ratio test (which compared the likelihood of the model with a null model with no explanatory variable). We did not include the proportion of the landscape composed of habitat suitable for scrub-jays as a covariate because distance-to-island-center (log-transformed) covaried with the amount of habitat within 1 km of the capture location of each individual, excluding ocean (Pearson’s r=−0.62; Supplementary Figure S3).

Our spatial test yielded support for the first prediction of the CMH; therefore, we conducted two post hoc analyses to determine how consistent this result was in different areas of the island and at different loci. To examine geographical consistency, we split the data set into two, with one data set including individuals captured west of the center of the island and the other including individuals captured east of the center of the island. For each side of the island, we tested for a relationship between HL and distance-to-island-center (log-transformed) using spatial error models and a log-likelihood ratio test, as described above. To examine consistency across loci, we performed tests on individual loci using a binary measure of whether an individual was homozygous at a particular locus. We analyzed these data using a logistic regression implemented using the glm function in R (R Core Team, 2016), and we used a log-likelihood ratio test to assess the level of support for distance-to-island-center (log-transformed) as an explanatory variable.

As an additional test of the first prediction of the CMH, we examined the spatial location of the peak in HL by performing a second-order polynomial trend interpolation using the 3D Analyst trend tool in ArcGIS (ESRI 2015). This method is useful for visualizing broad spatial trends because it fits a global model to a set of spatial data. For our purposes, it has the added benefit of allowing us to visualize the peak in HL without including distance-to-island-center in the model (that is, without making any assumptions about the importance of the center of the island).

Spatial variation in genetic differentiation

We used two methods to test whether the degree of localized genetic differentiation is greater toward peripheral regions of Santa Cruz Island (the second prediction of the CMH). Previous work documented isolation by distance within the Island Scrub-Jay population, showing that individuals on the western side of the island were most genetically differentiated from individuals on the eastern side of the island (Langin et al., 2015). However, that analysis did not test for spatial variation in the strength of isolation by distance, the aim of the present study.

First, we tested whether distance to the geographic center of the island was a predictor of genetic differentiation among individuals. We used SPAGeDi software (Hardy and Vekemans, 2002) to calculate Rousset’s a (Rousset, 2000), a metric of pairwise genetic differentiation between individuals. We were specifically interested in the degree of genetic differentiation among individuals located in the same region of the island, so we restricted our analysis to pairwise comparisons between individuals located 4 to 5 km apart from one another (a range of distances that is just beyond the maximum observed natal dispersal distance in Island Scrub-Jays located in the central region of the island; Langin et al., 2015), which amounted to a total of 13 775 pairwise comparisons. A subset of indidivuals (n=40) were not represented in the final data set because they were not captured within 4 to 5 km of another sampled jay. Next, we calculated the distance between (1) the geographic midpoint between each pair of individuals (the pair associated with each Rousset’s a value) and (2) the geographic center of the island. We tested for a relationship between Rousset’s a and distance-to-island-center (log transformed) using linear models (in base R) and an approach designed to avoid violating the assumption of independence among data points. This involved performing separate regression analyses on 1000 independently generated data sets, each of which contained pairwise comparisons that were independent of one another (that is, no individuals contributed to the calculation of >1 Rousset’s a value in a dataset). To generate each data set, we randomly reshuffled the order of the data, and—using an iterative process—selected one pairwise comparison per individual randomly, excluding data that were not independent from data that were already selected. The final data sets contained a total of 169 to 179 pairwise comparisons (the sample size was not equal across data sets because of the stochastic nature of the data selection process). We performed a separate linear regression on each of the 1000 data sets and report the mean value for the test statistics. For this analysis, we elected to use simple linear models rather than spatial error models because the majority (89%) of simple linear models did not exhibit spatial autocorrelation in the residuals.

As an additional test of spatial variation in genetic differentiation, we compared the strength of isolation by distance in different areas of the island. We predicted that the relationship between genetic distance and geographic distance would be steeper in more peripheral areas. We used the fishnet function in ArcGIS to group individuals into three separate regions (10 × 10 km each), distributed along the longest (east–west) axis of the island (see Supplementary Figure S4). We chose this spatial scale because grouping individuals into smaller regions (for example, 5 × 5 km) resulted in too few individuals per region. Within each region, roughly corresponding to the western (n=124), central (n=355) and eastern (n=65) portions of the island, we used SPAGeDi to estimate the slope of a regression between pairwise genetic distance between individuals (Rousset’s a) and ln-transformed geographic distance. The software uses a jackknife approach, removing one locus at a time, to calculate the mean and s.e. for each estimate. We compared the intercepts and slopes for each region, and inferred that isolation by distance was comparable in strength if the 95% confidence intervals overlapped one another.

Simulations

We conducted simulations in CDPOP (Landguth and Cushman, 2010)—a spatially explicit, individually based population genetics model—to examine ecological conditions that we hypothesized may be important for driving spatial variation in homozygosity in Island Scrub-Jays, specifically: (1) localized dispersal, (2) small total population size and (3) higher population density toward the center of the island. The spatial scale of dispersal would be expected to influence the extent of gene flow across the population, whereas total population size and the spatial distribution of individuals would be expected to influence the strength of genetic drift. In the simulations, we used input specifications that matched, as much as possible, the observed state of the current population (for example, natural observed levels of dispersal), as well as an alternate specification that represented a relaxation of that ecological condition (for example, greater dispersal distances).

To parameterize natural dispersal, we fit a negative exponential function to a data set of known natal dispersal distances (n=22; previously reported in Langin et al., 2015) and estimated parameters for the following negative exponential equation: relative probability of dispersal=A × 10−B × distance (result: A=17.2, B=0.0001652). We elected to use a negative exponential function because previous work found that it was the most appropriate function for describing dispersal patterns in terrestrial birds (Sutherland et al., 2000). We ignored sex-biased dispersal because few data were available for females (four females were in the dispersal data set), which may have caused us to underestimate overall levels of dispersal given that females disperse farther than males. To simulate relaxed dispersal (greater dispersal distances), we also assumed a negative exponential function and used the same A parameter but reduced the B parameter by an order of magnitude (B=0.001652). In the simulations, this resulted in an average dispersal distance of 803±7 m (mean±s.e.) for the natural dispersal scenario and 3753±8 m for the higher dispersal scenario.

We tested the effect of different population sizes and spatial distributions by varying the number and spatial arrangement of breeding locations in the input file. We assumed that the current breeding population of Island Scrub-Jays is 1134 individuals. This number was determined based on an October 2008 census population size estimate (Nc ~2268 individuals; Sillett et al., 2012) as well as the assumption that 50% of Island Scrub-Jays hold a breeding territory in a given year (rough estimate, based on our field observations of color-banded individuals near the center of the island). We also ran simulations that assumed a breeding population size that was double the current estimated size (2268 individuals). To specify the natural distribution of Island Scrub-Jays across Santa Cruz Island, we used a 300 × 300 m grid (n=2787 cells) and assigned 1134 individuals to the cells that had the highest predicted densities (based on data from Sillett et al., 2012), with no more than one individual per cell. We also considered three other combinations of population size/distribution by: (1) randomly assigning 1134 individuals to grid cells (current population size/random distribution scenario), (2) assigning two individuals to each of the 1134 grid cells that had the highest predicted densities (higher population size/natural distribution scenario) and (3) randomly assigning 2268 individuals to grid cells (higher population size/random distribution scenario).

We used CDPOP to simulate all combinations of the above dispersal, population size and distribution specifications, holding all other variables constant. The basic steps for each generation were as follows: (1) individuals mate with a neighboring individual of the opposite sex up to a distance of 1 km from their location (average distance to find mate across simulations was 486±4 m), (2) all adults die and (3) offspring disperse according to the specified dispersal function. The breeding locations specified in the input file were constant across generations, so only 1134 or 2268 individuals (depending on the population size of a given scenario) secure a breeding location each generation. Each individual in our initial population was randomly assigned a gender and a genotype (12 loci with starting diversities of 15 alleles each, corresponding to the number of loci and average allelic diversity in our empirical microsatellite data set). See Supplementary Table S1 for a complete list of all relevant parameter specifications. We performed 20 simulations for each dispersal/population size/distribution scenario (160 simulations total) and ran each simulation for 1000 generations. Using data from the last generation, we calculated the difference in HL between (1) the 10% of individuals closest to the center of the island and (2) the 10% of individuals furthest from the center of the island. We performed an analysis of variance in R where the difference in HL (between the peripheral and central portions of the island) was the response variable and the dispersal, population size and distribution treatments were categorical variables. All possible interaction terms were included initially and were dropped from the final model if they were not significant. As a post hoc analysis, we examined the nature of significant interactions using the ‘testInteractions’ function in the R package phia, which holds factor levels constant while testing for variation in response to other factors.

Results

Central–marginal hypothesis

We found support for the first prediction of the CMH. Island Scrub-Jays located toward the periphery of the island were more homozygous (higher HL values) than individuals located toward the center of the island (D=16.2, P=0.0001, d.f.=1, n=533; Figure 2). The magnitude of the trend in HL is such that we would expect an individual located 18 km from the center of the island to be heterozygous at 8% fewer loci than an individual located 1 km from the center of the island (assuming loci are neutral and expected heterozygosity is constant across loci). The same pattern was detected when restricting the analysis to individuals that were captured on the western (D=5.7, P=0.02, d.f.=1, n=198) and eastern (D=8.1, P=0.004, d.f.=1, n=335) sides of the island; it was also detected at several loci when data were analyzed separately for individual loci (four of 12 loci exhibited significantly higher homozygosity toward the island periphery (P<0.05), and 11 of 12 loci trended in that direction; Supplementary Table S2). Another post hoc analysis, which fit a second-order polynomial function to the spatial data, provided additional support that HL values decline away from the geographic center of the island (Figure 3).

Figure 2
figure 2

Homozygosity (HL) increased with distance from the geographic center of Santa Cruz Island (P=0.0001; n=533), consistent with the central–marginal hypothesis. The same pattern was observed on the eastern and western sides of the island. Note the log scale on the x axis; the values 3.0 and 4.2 correspond to the distances 1 and 16 km, respectively, relative to the geographic center of the island.

Full size image
Figure 3
figure 3

Surface depicting the broad spatial pattern in homozygosity (HL) across Santa Cruz Island, based on a second-order polynomial trend analysis. Lighter colors correspond to locations with higher predicted HL values. White circles represent sample locations, the white cross depicts the geographic center of the island and lines show contours along the predicted HL surface. The darkest region—corresponding to locations with the lowest levels of homozygosity—roughly corresponds to the center of the island.

Full size image

In contrast to homozygosity, we did not find evidence of greater genetic differentiation toward the periphery of the island (that is, more localized differentiation than expected based on isolation by distance). Distance-to-island-center was not a significant predictor of pairwise genetic distance between individuals located 4 to 5 km from one another (average test statistics for regressions on 1000 independent subsets of the data: t=0.7, P=0.48; n=169 to 179 pairwise comparisons per regression). Furthermore, the strength of isolation by distance was comparable in the western, central and eastern regions of the island (Table 1). In both analyses the trend was in the predicted direction—stronger isolation by distance toward the island’s periphery—but the results were not statistically significant.

Table 1 Comparison of the strength of isolation by distance within regions roughly corresponding to the western (n=124 individuals), central (n=355 individuals) and eastern (n=65 individuals) portions of the island (see Supplementary Figure S4)
Full size table

Simulations

Simulations revealed factors that may explain the presence of spatial variation in homozygosity in Island Scrub-Jays. We found that the magnitude of the homozygosity (HL) differential between the population center and the population periphery was predicted by dispersal (F1, 159=56.8, P<0.0001), total breeding population size (F1, 159=4.6, P=0.03) and an interaction between dispersal and population size (F1, 159=5.7, P=0.02; see Figure 4). Spatial variation in density—specifically, whether individuals were randomly distributed across the landscape or occurred at higher densities toward the population center—was not a significant predictor of spatial variation in HL (F1, 159=0.8, P=0.38). A post hoc test revealed that the HL differential was consistently higher (that is, peripheral individuals were more homozygous relative to central individuals) in simulations that assumed extremely localized dispersal (observed mean dispersal distance ~0.8 km) than in simulations that assumed greater dispersal distances (observed mean dispersal distance ~4 km). This was the case regardless of whether the breeding population size was smaller (interaction test holding population size constant while varying dispersal; F1, 159=49.4, P<0.0001) or larger (F1, 159=13.2, P=0.0004). Furthermore, the HL differential varied as a function of population size in the low dispersal scenarios (interaction test holding dispersal constant while varying population size; F1, 159=10.3, P=0.003) but not in the high dispersal scenarios (F1, 159=0.0, P=0.86), indicating that the significant interaction between dispersal and population size was due to small population size exacerbating the HL differential in low dispersal scenarios.

Figure 4
figure 4

The difference in homozygosity (HL) between the central and peripheral portions of the population in simulations as a function of dispersal (lower versus higher), breeding population size (current versus higher) and spatial distribution pattern (natural versus random). Values greater than zero on the y axis indicate that homozygosity was elevated along the population periphery. Each panel shows the results of models that assumed a certain population size (denoted above panel) and distribution pattern (denoted to the right of panel). These results show that HL was most likely to be elevated along the periphery of the population when dispersal and population size were both low. The solid black circle represents the value calculated from the empirical Island Scrub-Jay data set; it is overlaid on results for the simulation category that was parameterized based on data from the current Island Scrub-Jay population (lower dispersal, current population size, natural distribution). Each category has a sample size of 20 simulations. Boxes represent the interquartile range (IQR); whiskers extend to 1.5 times the IQR; open circles are outliers.

Full size image

Discussion

Spatial variation in genetic drift and gene flow is predicted to generate differences in the genetic properties of populations at the center versus the periphery of species’ ranges. Here, we demonstrate that Island Scrub-Jays located toward the periphery of Santa Cruz Island are more homozygous than individuals located toward the center of the island. This finding is consistent with the first prediction of the CMH (Eckert et al., 2008), as well as previous studies that detected lower genetic diversity toward the range margin in a variety of taxa (see, for example, Lammi et al., 1999; Schwartz et al., 2003; Micheletti and Storfer, 2015). However, most studies found that genetic diversity was lower in peripheral populations, not along the periphery of a single population, as we found here. The presence of such fine-scale variation in genetic diversity is remarkable given that the maximum distance an individual was sampled from the geographic center of Santa Cruz Island was only 18 km. This finding indicates that microevolutionary processes that give rise to broad-scale variation in genetic diversity among populations can also be important for generating fine-scale variation in genetic diversity within populations.

Even though habitat is more sparsely distributed toward the periphery of Santa Cruz Island (Supplementary Figure S3), we did not find support for the second prediction of the CMH: the magnitude of genetic differentiation did not increase toward the island periphery. This could reflect a lack of power to detect subtle differences in the strength of isolation by distance at a local scale, especially given that the observed trend was in the predicted direction. Nevertheless, it is consistent with previous findings that habitat patchiness is not an important factor shaping population genetic structure in the Island Scrub-Jay (Langin et al., 2015) or in the species’ closest relative, the California Scrub-Jay (A. californica; McDonald et al., 1999; although note that the opposite was found for the Florida Scrub-Jay (A. coerulescens); Coulon et al., 2010). Thus, Island Scrub-Jays may not exhibit spatial variation in genetic differentiation because existing habitat gaps, even the larger ones toward the island periphery, are not wide enough to impede gene flow (that is, peripheral areas are still connected via dispersal with other parts of the island).

It is worth noting that our genetic differentiation results do not imply that peripheral regions of the island receive the same levels of gene flow as central regions. In fact, peripheral regions likely receive fewer immigrants because dispersal events can originate from fewer directions (Schwartz et al., 2003). For example, immigrants to Scorpion Canyon, an area with suitable habitat on the northeast side of Santa Cruz Island, can only originate from areas to the south and to the west, whereas immigrants can originate from any direction in the central portion of the island (see Figure 1 for distribution of suitable habitat). This potential for lowered net gene flow along the island periphery—because of the geometry of the population and not spatial variation in connectivity—may explain why we found support for the first (genetic diversity) but not the second (genetic differentiation) prediction of the CMH.

Previous studies designed to test the CMH have been criticized for incomplete sampling (Eckert et al., 2008; Guo, 2012) because drawing firm conclusions about the importance of range peripherality is challenging when all peripheral population samples originate from the same geographic area (for example, the northern range limit). That was not an issue in the present study, as we sampled Island Scrub-Jays extensively across the species’ entire (although small) geographic range, obtaining samples from a quarter of the total population (Nc ~2300 individuals; Sillett et al., 2012). This enabled us to confirm that the same trend in HL was observed on the eastern and western sides of Santa Cruz Island. Although the magnitude of the trend was not substantial and there was considerable scatter (Figure 2), most tests of the CMH have also reported minimal yet statistically significant differences in genetic diversity between central and marginal populations (Eckert et al., 2008).

Our findings are also consistent across loci. We detected the same pattern—higher homozygosity toward the island’s periphery—for several loci (Supplementary Table S2), indicating that the trend in Figure 2 was not driven by variation at a single locus. If the same pattern holds genome wide, then an 8% increase in homozygosity along the island’s periphery could translate into a sizeable effect. That said, our findings may not apply to loci under selection because neutral genetic variation is not a strong predictor of adaptive genetic variation (McKay and Latta, 2002). For example, in the San Nicolas Island Fox (Urocyon littoralis dickeyi), which occurs on a smaller nearby island, individuals are monomorphic at neutral loci (microsatellites) but have relatively high levels of genetic variation at loci within the major histocompatibility complex (Goldstein et al., 1999; Aguilar et al., 2004). High major histocompatibility complex diversity might be maintained by balancing selection, despite strong genetic drift within the small, isolated population, because the set of genes is important for immune function (Aguilar et al., 2004). Thus, future work measuring variation across a larger portion of the Island Scrub-Jay genome (for example, single-nucleotide polymorphism assays) will be needed to determine whether our findings are broadly reflective of spatial patterns in homozygosity at neutral and adaptive loci.

Previous studies have argued that patterns consistent with the CMH may not be a product of contemporary processes, and that peripheral populations may harbor the historical legacy of founder effects from more recent colonization events (for example, because of historical range shifts during periods of climate change; Eckert et al., 2008). This explanation does not appear to be a mechanism that has given rise to spatial variation in genetic diversity in our study system. Aphelocoma jays have been present on California Channel Islands for an estimated 1 million years (McCormack et al., 2011) and sea level rise since the Pleistocene has reduced the size of the islands (Rick et al., 2014). Santa Cruz Island did undergo substantial habitat alterations in the nineteenth and twentieth centuries because of the presence of introduced herbivores (Morrison, 2007). However, even in 1985—around the time management agencies began removing introduced animals—habitat suitable for Island Scrub-Jays persisted in peripheral areas of the island (Sillett et al., 2012), including in nearly all of the areas that were sampled for the present study. A population bottleneck and/or localized extinctions could have occurred during the period when feral herbivores were present on the island. However, we found no evidence of recent genetic bottlenecks in the western, central and eastern portions of Santa Cruz Island (see Supplementary Text and Supplementary Table S3).

The predictions of the CMH are based, in part, on the observation that peripheral populations often occur at lower densities, and therefore are expected to experience stronger genetic drift. The density of Island Scrub-Jays declines with distance from the center of Santa Cruz Island (Supplementary Figure S2). However, based on our simulation results, these density differences do not appear to be important for generating higher levels of homozygosity toward the periphery of the island. Simulation outcomes did not differ depending on whether individuals were (1) distributed randomly across the landscape or (2) more densely packed at the center of the island. Genetic drift was still operating in the population as a whole: allelic diversity—a proxy for the overall level of genetic drift in the population—declined over time in all simulations and, as one would expect, was consistently lower in simulations with small total population sizes (see Supplementary Figure S5). However, the strength of genetic drift did not appear to vary spatially, even when the distribution of individuals was skewed toward the center of the island. Studies that have documented patterns consistent with the CMH have generally assumed that spatial variation in density played a role, but few studies have actually tested the mechanisms generating those patterns (Eckert et al., 2008). Evaluating whether spatial variation in population density is important under certain conditions, but not others, will ultimately require a broader range of simulations, including those that consider multiple populations distributed across a larger spatial scale.

In contrast to our findings with density, simulation results revealed that spatially restricted gene flow (localized dispersal) was critical for generating higher homozygosity toward the island’s periphery. For all combinations of population size and spatial variation in density, the HL differential was highest for simulations that assumed low dispersal (~0.8 km) and was close to zero for simulations that assumed greater dispersal distances (~4 km). Based on these results, it appears that peripheral areas of the island—locations where immigrants can arrive from fewer directions—have a lower probability of replenishing variation that is lost locally because of genetic drift, especially if the spatial scale of gene flow is small enough. The importance of localized dispersal does not come as a surprise, as few would expect a panmictic population to exhibit patterns consistent with the CMH. However, these results do reveal that the spatial scale of gene flow must be highly restricted within a population to generate spatial variation in homozygosity, at least for the range of parameterizations considered in this study. They also reveal that the effect of localized dispersal appears to be exacerbated when population size is low (and thus when the overall level of genetic drift in the population is high), as the HL differential was highest in simulations with low dispersal and small total population size. Collectively, we interpret these findings to mean that the spatial scale of gene flow and the overall strength of genetic drift in the population interact to determine whether individuals along the periphery have elevated homozygosity.

Research on fine-scale variation in the genetic properties of populations on islands could be useful for designing management strategies for species of conservation concern, an important task given the high rates of endangerment and extinction on islands (Johnson and Stattersfield, 2008). Conservation biologists have long recognized that founder effects and chronic genetic drift make island-endemic species more susceptible to problems associated with low genetic diversity (Jamieson, 2007; Frankham, 2008). Our findings suggest that localized dispersal may exacerbate that problem, causing even lower levels of genetic diversity in some segments of the population. In the case of the Island Scrub-Jay, future research should examine issues like inbreeding depression and disease susceptibility in multiple areas of the island, rather than treating the species as one homogenous population. If problems are detected, translocation of individuals within Santa Cruz Island could replenish local levels of genetic diversity, while being mindful of the possibility of outbreeding depression (Frankham et al., 2011).

Conclusions

The Island Scrub-Jay is one of the rarest and most geographically restricted bird species in North America. Here we present evidence that homozygosity, but not genetic differentiation, is higher toward the periphery of the species’ range, providing partial support for the CMH. Through simulations, we also demonstrate that localized dispersal and small total population size, but not spatial variation in density, were important factors underlying the generation of spatial variation in homozygosity within this population. Such variation in genetic diversity is more typically associated with species that are broadly distributed and that have disjunct populations toward the edge of their range. Here we show that, if the spatial scale of gene flow is small enough, the CMH can apply to narrowly distributed species. Localized dispersal is common across a wide range of taxa (Sexton et al., 2014), suggesting similar patterns might be common in nature. Thus, future studies should consider testing for spatial variation in genetic diversity at fine spatial scales—even within a single population.

Data archiving

Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.25qg7.