Introduction

Many populations of organisms are naturally spatially structured. For instance, populations with continuous ranges but limited dispersal ability exhibit marked spatial structure (Slatkin, 1985), whereas geographic features such as rivers or mountain ranges may act as barriers leading to disjoint patterns of population genetic structure that may lead to speciation (Avise et al., 1987; Gompert et al., 2014). However, population genetics studies traditionally treat geographically separated populations as genetically panmictic units, oftentimes where this assumption does not match the ecological attributes of the taxa under study. Nonetheless, there has long been interest in using spatial models for understanding processes underlying geographical variation in genetic polymorphisms (Wright, 1946; Kimura and Weiss, 1964). Spatial genetic models that investigate spatial and temporal dynamics remain an active area of research in population genetics (see for example Pieschl et al., 2013) and are becoming increasingly useful with the widespread availability of genome-scale data and computational power to generate more complex and realistic models that better reflect biological reality (Gompert et al., 2014).

Traditionally, population structure has been modeled by dividing a population into discrete subpopulations or demes that can be interconnected via migration. Many variations of this type of model exist, including the finite island model (Wright, 1943) and one- and two-dimensional stepping stone models (Kimura and Weiss, 1964), that differ in the assumption of how migration between demes occurs. Backward-in-time discrete population structure can be modeled using the structured coalescent that comes in several forms (Tellier and Lemaire, 2014). Such discrete models of population structure have been successfully incorporated into inferential methods such as SPLATCHE (Currat et al., 2004) that explore complex demographic scenarios. Yet, despite these significant advances since Wright’s keystone work, explicitly incorporating spatial structure into genetic models remains a challenging task because a key feature of the standard coalescent (Kingman, 1982), lineage exchangeability, does not hold under the structured coalescent (Wakeley and Aliacar, 2001). This is because the history of samples under a spatial framework depends not only on the number of lineages that exist at any point in time but also on their location (Wakeley and Aliacar, 2001).

Alternatively, population structure has been modeled under the metapopulation paradigm, where demes undergo local extinction and recolonization. The metapopulation paradigm was extended to population genetics by Slatkin (1977) and later generalized by Whitlock and McCauley (1990). In the latter model, a metapopulation is divided into D equally sized demes with generations being discrete and non-overlapping. At the start of a generation, a fraction of the D demes go extinct, and are recolonized by either a migrant pool (where gametes can be from different demes) or a propagule pool (where all gametes are guaranteed to be from the same deme). Under this model, Whitlock and McCauley (1990) derived an analytical formula for FST, and showed that FST is directly proportional to the number of demes recolonized by the migrant pool.

Later, in a seminal paper, Wakeley and Aliacar (2001) showed that genealogical processes in a metapopulation commonly involve a separation of timescales. This backward-in-time process includes two phases: a ‘scattering phase’, where each sampled deme contains multiple sampled lineages that either migrate between demes or coalesce, and a ‘collecting phase’, essentially the Kingman coalescent rescaled to a different effective size according to the number of demes. Using simulations these authors derived expectations for the number of segregating sites and the distribution of the site frequency spectrum under this model for different migration, extinction and recolonization rates. Later, Wakeley (2004) showed that gene genealogies from the Whitlock and McCauley (1990) model have the same structure as Wakeley and Aliacar (2001) when the number of demes is large, and hence that simulated gene genealogies under the Wakeley and Aliacar (2001) model can be used for historical inference in systems that meet the assumptions of Whitlock and McCauley (1990). Indeed, similar models based on the work of Slatkin (1977) have also been used to quantify genetic differentiation and to analyze the consequences of population turnover on effective population size (see, for example, Wade and McCauley, 1988).

In the absence of better analytical alternatives, metapopulation and island models rely on defining deme-specific migration rates to capture explicit spatial structure. However, deme-specific migration rates are limiting in that they require a large number of parameters to be defined, and do not allow for changes in spatial distribution of existing demes through time. In addition, if migration rates between demes are uneven, fixing population size introduces the problem of conservative migration (Wakeley, 2009), where the number of lineages migrating out of a deme is not necessarily equal to the number of lineages migrating into it.

More recently, Etheridge (2008) and Barton et al. (2010a, 2010b) provided an analytical solution to the spatially explicit coalescent by developing a model of extinction and colonization in a spatial continuum. Here denoted as the continuum model, this model is similar to metapopulation models in that it uses patterns of extinction and recolonization to create a coalescent that captures spatial patterns. However, in contrast to strict metapopulation models, the continuum model allows individuals to be freely distributed in continuous space instead of grouped in spatially fixed demes. In doing so, the effective population size of local demes and migration rates between demes are no longer of concern. In addition, the continuum solves several long-standing problems with coalescent models in continuous space. In particular, defining a coalescent model with a uniformly dense population where lineages move in two-dimensional continuous random walk and coalesce when sufficiently close has been shown to be inconsistent (Barton et al., 2010a). This is because lineages that move independent of population density violate the assumption of uniform density (Barton et al., 2010a).

The genealogical process for the continuum model has been well characterized, and therefore could be useful for inference based on spatially explicit genealogical reconstruction of genetic data. Specifically, this model has the capability of detecting spatial effects on demographic histories, and in so doing, more accurately elucidate realistic demographic processes. However, the empirical utility of the continuum model for demographic inference has not been explored, and hence its value for inference of real biological populations remains uncertain. To address this issue, we incorporate the spatial continuum model into an approximate Bayesian computation (ABC) framework for parameter estimation using genomic data. We choose to estimate two population genetic parameters: neighborhood size (NS) and dispersal radius (R).

Neighborhood size (Wright, 1946) was originally introduced as a continuous space analog to effective population size in Wright’s isolation-by-distance model (Charlesworth and Charlesworth, 2010). In this model individuals are assumed to be uniformly distributed along a line or plane. The birthplace of an individual is typically assumed to be a normal random variable with the center of the distribution at the parent’s point of origin. In this way, birth events take on the characteristics of a random walk. This leads to a natural way to define Ns. In the Kingman coalescent the rate of coalescence for a pair of lineages is , where N is the effective population size. Therefore, it is reasonable to define as the rate of coalescence under isolation-by-distance model. A calculation shows that in two dimensions NS=4πσ2D, where D is the effective population density and σ the s.d. of the random variable above. From here it can be seen that NS is the number of individuals within a circle of radius 2σ (Charlesworth and Charlesworth, 2010). The s.d., σ, is referred to as the dispersal rate. Additional theoretical results show that small neighborhood sizes correspond to high genetic differentiation between localities, whereas large neighborhood sizes of approximately ⩾1000 individuals correspond to lower genetic differentiation between localities (Charlesworth and Charlesworth, 2010). Whereas this definition of neighborhood size is not without the difficulties mentioned above, Barton et al. (2013) provide a new definition of Nsfor the continuum model that can be similarly used to infer spatial structure.

In the continuum model, dispersal radius has a slightly different interpretation than the dispersal rate of the isolation-by-distance model. Dispersal radius in the former model, denoted R, refers to the maximal distance an offspring is born away from its parent’s place of origin. Hence, the dispersal radius is an upper bound for dispersal, whereas in the isolation-by-distance model, dispersal rate is not.

To demonstrate the utility of the continuum model for demographic inference, we simulate gene genealogies using the Discsim simulator (Kelleher et al., 2014). We then use the retained gene genealogies to generate corresponding DNA sequences that could be compressed into an array of classical summary statistics that have no information about space or deme identity (Alvarado-Serrano and Hickerson, 2015). Subsequently, we use this simulation pipeline to build an ABC framework for the estimation of the two parameters of interest: neighborhood size and dispersal radius. Finally, we apply our method to a shrub species endemic to the Little Karoo, Berkheya cuneata, to infer neighborhood size and dispersal radius of the population.

Materials and methods

To expand the capability of the continuum model for inferring relevant demographic parameters that determine population structure under a spatial coalescent framework, we coupled the spatial coalescent continuum model—simulated using the Python library Discsim (Kelleher et al., 2014) and its software dependency Extinction/Recolonization Simulator (ERCS, Kelleher et al., 2013)—with a DNA sequence simulator, Seq-Gen (Rambaut and Grassly, 1997) and an ABC analysis routine (Csilléry et al., 2012). The accuracy and utility of this procedure was first tested through simulation-based cross-validation (Bertorelle et al., 2010) and then through an empirical implementation.

Although several variations on the continuum process exist, we focus here on the ‘disc model’, for which the corresponding coalescent model is implemented in Discsim. Briefly, a population of D individuals is distributed uniformly upon a torus of side length L. Movement and reproduction are captured through disc-shaped events that occur throughout the sample area. Forward in time, individuals within the radius of an event are removed with probability u, and replaced by a Poisson-based number of offspring that are placed within the affected area. Recombination between adjacent loci occurs with a fixed probability (r). Events occur at random locations with a specified event radius, R, and at an exponentially distributed rate λ. Individuals are assumed to remain stationary throughout their adult lifetime, as would be the case with plants and many marine invertebrates.

Following the convention proposed by Kelleher et al. (2016), we define generation time as the expected time until an individual is removed by an event. Thus, 1 generation is equal to units of simulation time (Kelleher et al., 2014, 2016). For this reason, the event radius can be equated with a ‘dispersal radius’. Dispersal radius refers to a lineage’s ability to move away from their point of origin between generations (that is, the maximal distance an individual born in an event is placed away from its parents).

Backward in time, the coalescent process for a sample of n individuals proceeds event by event (Kelleher et al., 2014) as the ancestors of each individual are traced through time. Events occur at a rate λ, and land at uniform random locations within the landscape. A single event may or may not affect an individual, depending on how close the event center is to individual lineages and the removal probability. If an individual is removed, it is replaced by its parents at uniform random locations within the radius of the event. A coalescent event occurs when two or more samples are removed by the same event. Events where only a single individual is removed represent between-generation movement within the landscape. If a population with two parents is simulated, loci are distributed to parents based on the recombination rate. In some cases this means all loci descend from a single parent (that is, no recombination occurs), and in others this means loci descend from two parents (that is, recombination occurs).

In this model the compound parameter neighborhood size (Wright, 1946), here denoted NS (denoted N in Barton et al., 2013; Kelleher et al., 2014), is directly related to the removal rate u. For populations with v parents, NS is defined to be (Barton et al., 2013). Going backward in time, the number of parents (v) determines how many ancestors replace individuals removed by an event, and therefore determines the maximum number of ancestors that loci can be distributed to. Thus, neighborhood size refers to the number of individuals within the area of an event of radius R. The resulting gene genealogy for each simulated locus is retained and can be used for further analyses.

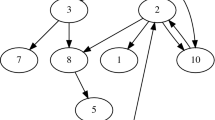
To test the ability of our pipeline to estimate NS, we defined a torus with a side length (L) of 100 arbitrary units. We then placed 8 individuals at fixed locations within the torus (Figure 1). Each sample had 10 freely recombining loci. The resulting gene genealogies were then used to simulate DNA sequences for ten 1000-bp loci using the program Seq-Gen (Rambaut and Grassly, 1997). DNA evolved according to the Hasegawa, Kishino and Yano (HKY; Hasegawa et al., 1985) mutation model, with parameters for the mutation model (Table 1) selected from Posada and Crandall (2001) and an assumed mutation rate of 1.1 × 10−8 mutations per generation (Roach et al., 2010). Variation in the resulting sequences was summarized by six classical population-level summary statistics (Supplementary Table S1) calculated using the program Arlequin (Excoffier et al., 2005). We ran 100 000 replicates to test the pipeline’s ability to estimate NS (Table 1). Simulations took ∼2 days on a 12-core computer. In these simulations, event radius, R, was fixed to 2.0 space units, and event rate, λ, was fixed to 1.0 units of simulation time. For each replicate, NS was randomly drawn from a discrete uniform distribution between 3 and 200 individuals within the area of an event.

Figure 1
figure 1

Sample placement within the landscape. Starting sample coordinates of 8 individuals within a torus with side length 100. These sample coordinates were used to assess the ability to estimate neighborhood size.

Full size image
Table 1 Mutation model and simulation parameters
Full size table

Finally, we coupled the genetic data simulated under our models (Table 1) into an ABC framework (Csilléry et al., 2012) to formally estimate NS. We assessed parameter estimation performance based on ABC cross-validations. We ran 100 cross-validation replicates with a 5% tolerance and a local-linear regression algorithm (Beaumont et al., 2002) using the ‘leave-one-out’ procedure implemented in the cv4abc() function in the ‘abc’ R package (Csilléry et al., 2012). Performance of the cross-validation replicates was assessed using the overall cross-validation prediction error that corresponds to the sum of the square difference between the true and estimated parameter values, divided by the variance of the true parameter times the number of cross-validation replicates (Csilléry et al., 2012). All ABC calculations were carried out in R v. 3.0.2 (R Development Core Team, 2013) using the package ‘abc’ (Csilléry et al., 2012).

Empirical application

The Little Karoo is an approximately 290 km wide by 60 km long valley that is part of the Greater Cape Floristic Region in South Africa. It is located between the Langeberg and Outeniqua mountains to the south and the Witteberg and Swartberg mountains to the north (see Figure 1 in Potts et al., 2013). Berkheya cuneata, of the family Asteraceae, is a small perennial shrub endemic to this region. B. cuneata is insect pollinated, wind-dispersed and widely distributed within the basin (Potts et al., 2013). The distribution and endemism of B. cuneata make it a well-suited study system for the use of the continuum model. For our analysis we use the data generated by Potts et al. (2013) who collected samples of 47 individuals across 34 sites in the Little Karoo together with GPS coordinates for all samples. From these samples, Potts et al. (2013) extracted genomic DNA and sequenced two chloroplast DNA loci, trnQ(UUG)-5rps16 and psbD-trnT(GGU) (Shaw et al., 2007), as well as one nuclear DNA locus from the ITS region of the 18S-26S cistron.

Using our inferential approach, we estimated NS and R of B. cuneata, and thus were able to roughly approximate the local population density of B. cuneata. For this analysis, the length of the side of the torus was defined to be 200, where 1 unit simulation distance was equal to 1 km. Thus, a side length of 200 simulation units corresponds to 200 km, the approximate range of B. cuneata (Potts et al., 2013). Nuclear loci were phased using the program fastPhase (Scheet and Stephens, 2006). Because of computational limits only a single individual per sampling location was used. A total of 33 samples were placed at locations in the simulation area corresponding to their GPS coordinates (one sampling location was removed because of lack of nuclear data). Because relatively little is known about the full dispersal range of B. cuneata, dispersal events had a variable radius (R) between 1.0 and 10.0 km. A variable removal rate equivalent to NS between 10 and 1000 individuals was used. The event rate (λ) was fixed to 1.0 unit of simulation time. Simulations were run using two parents and two loci, treating all chloroplast DNA loci as a single haploid unit to match expected patterns of inheritance. A total of 100 472 simulations were run over 36 days across two 10-core computers. The mutation rate was set to 1.25 × 10−8 mutations per generation for chloroplast DNA and 3.475 × 10−8 mutations per generation for nuclear DNA with a 5-year generation time (Wolfe et al., 1987). Summary statistics for the B. cuneata data set were calculated with Arlequin (Excoffier et al., 2005), and used to estimate NS following an ABC procedure implemented in the R package abc() under the 5% tolerance and the standard rejection algorithm (Tavare et al., 1997). We choose the rejection algorithm, rather than local linear regression, because the local linear regression algorithm transformed all inferred parameter values outside of the prior distribution (Wegmann et al., 2010). To test the robustness of our inference, we simulated an additional 5000 replicates drawing from the posterior distribution of inferred parameters, and performed a graphical check using principal component analysis (Chan et al., 2014).

Results

Estimator performance

Our ABC pipeline showed a strong ability to estimate the NS parameter. Analysis of 100 cross-validation replicates showed a strong association between true NS, the value used to run the simulation, and the NS estimated by our pipeline (Figure 2). The cross-validation prediction error, a measurement that quantifies the difference between the true and estimated parameter values, was 0.13. Accordingly, the R2 of a regression between the true and estimated parameters for N was 0.87 (P-value <2.2 × 10−16).

Figure 2
figure 2

Performance of ABC parameter estimation across 100 cross-validation replicates. ABC performance for estimating neighborhood size (NS). The x axis is the parameter value used to run the simulation; the y axis is the corresponding parameter estimated by ABC. The diagonal line is a 1:1 line. Cross-validation prediction error for these data is 0.13.

Full size image

Empirical application

ABC analysis of the B. cuneata samples yielded estimates of median R of 7.33 (95% highest posterior density interval (HPDI) 2.44–9.86; Figure 3) and a median NS of 502.50 (95% HPDI 56.03–962.00; Figure 3). Density plots of the prior parameter values for R and NS showed uniform coverage of the prior parameter space, whereas retained posterior simulations showed distinct peaks in parameter values (Figure 3). This is a strong indication of our summary statistics power to differentiate between sets of parameter values, and supports the quality of our inference.

Figure 3
figure 3

Posterior density plots of estimated parameters. Posterior density plots of retained simulations for the B. cuneata data set obtained using a rejection algorithm with a tolerance of 5%. The dotted line is the prior density. The solid line is the posterior density. Vertical lines indicate the median parameter value. (a) Posterior parameter density retained for the event radius, R. (b) Posterior parameter density retained for neighborhood size, NS.

Full size image

To test the goodness of fit of our model and investigate whether our model can generate the empirically observed data, we performed a principal component analysis on the summary statistics of 5000 posterior replicates. Parameters of the posterior replicates were drawn from the inferred posterior distribution of our pipeline. A plot of the first two principal components (Figure 4), which together explained over 99% of the variance within this data set, along with the principal component-projected observed data set, showed that the observed data set closely matched that of the posterior replicates, and hence our model does fit the observed data.

Figure 4
figure 4

Principal component analysis of replicates drawn from the posterior predictive distribution. Principal component analysis of 6 summary statistics from 5000 replicates simulated from parameter values drawn from the inferred posterior distributions. The gray square marks the observed data set.

Full size image

Discussion

Our results indicate that we can successfully estimate NS with a high degree of accuracy. Ability to estimate neighborhood size is important for several reasons. First, our tool can test hypotheses of spatial structure as NS directly relates to this quantity. Second, neighborhood size is a proxy for two biological meaningful parameters, population density and population size. Because neighborhood size in the continuum is the number of individuals within the area of an event, this parameter, along with event radius, is a proxy for population density. As expected, a large neighborhood size corresponds to dense populations. Although nontrivial in practice, if the distribution of a population is well known, density gives an approximation of the total population size within this predefined area. In our simplified example, the event radius, and thus dispersal radius, was fixed. Although this may seem like an oversimplification in a model intended to be a proof of concept, fixing R is not unreasonable if there is information about the dispersal ability of the population of interest. For instance, the event radius could be set to the maximum dispersal potential of an individual.

Another important advance that comes out of this study is a new way to accommodate space into historical population genetic inference while relaxing the necessity to assign individual genotypes into demes. Ideally, one could extend this pipeline to incorporate environmental and spatial heterogeneity in habitat suitability over time and space while accommodating historical cycles in demographic parameters (Alvarado-Serrano and Hickerson, 2015), analogous to the way SPLATCHE (Currat et al., 2004) incorporates environmental heterogeneity. In this way more complex scenarios that better capture the natural complexity of biological systems could be modeled. Such increased complexity may introduce new theoretical difficulties, namely, theoretical results become difficult to generalize or even to derive, as the model gets closer to any specific empirical system. Such cases could however be easily explored using our proposed simulation pipeline and modifications to the Discsim package. Hence, our coupled ABC pipeline is expected to provide a valuable tool for implementing model-based demographic inference of spatially structured populations under these novel coalescent models.

Empirical application

Our results showed that B. cuneata in the Little Karoo have the ability to disperse a median of 7.3 (95% HPDI 2.4–9.8 km), and have a median estimated neighborhood size of 502.50 (95% HPDI 56.03–962.00) individuals within their dispersal range. Although the point estimates would lead us to perhaps expect to observe ∼3.0 individuals per km2 on average, the densities are likely to be substantially higher based on empirical evidence. Although B. cuneata is common in Little Karoo, and in some cases hundreds of individuals can be found within a hectare (A Potts, personal correspondence), our estimate of population density is dependent on the effective population size of breeding individuals rather than actual sizes, and hence the effective densities of B. cuneata could indeed be much lower than the observed number of individuals. In addition, the continuum model assumes that the population is uniformly distributed, but B. cuneata has recently experienced a range contraction (Potts et al., 2013), and because of geographic barriers it has a patchy distribution. Therefore, our estimates are best interpreted as an average across the entire region including unoccupied areas.

Investigation of the posterior density of the dispersal radius R showed a tighter distribution when compared with the NS, indicating a better ability of our pipeline to estimate this parameter given the observed data. Given the empirical data, the HPDI for R covered 82% of the prior, whereas the HPDI for NS covered 92% of the prior. Inspection of the principal component analysis indicated that our observed data set fell close to, if not within, the range of data sets simulated from the posterior predictive distribution, thereby indicating that our inferential model can generate data close to the observed data. An increased number of simulations and using wider priors would presumably allow for better resolution of posterior densities, as the retained simulations would more closely match the observed data set.

Because of computational limits, it is not efficient to simulate sufficiently large numbers of samples from priors that span overly large NS values as the waiting times to coalescence in space increases nonlinearly. However, several alternatives exist. Discsim allows for simulations in either one- or two-dimensional space. Simulations in one dimension take place along a circle, rather than a torus, and are much more computationally efficient. This allows efficient modeling of continuous populations with large densities, but does lose some spatial information. In addition, new methods such as ‘approximate approximate Bayesian computation’ (Buzbas and Rosenberg, 2015) are potentially able to estimate the posterior distributions inferred by ABC methods with substantially fewer simulations and when this novel approach becomes sufficiently developed may prove to be ideally suited to make inference under the continuum model.

Barton et al. (2013) outlines an analytical approach for estimating NS based on observed recombination events along long sequence blocks, and use this to date coalescent events. They show that for large NS this approach works well, but estimation is more difficult over smaller NS. This is because NS partially determines the local rate of coalescence. If lineages coalesce too quickly, recombination events go unobserved because there are no mutations to distinguish them. Our method here demonstrates that if a sufficient number of individuals are sampled we can accurately infer smaller NS, and that it is computationally tractable to do so.

Although here we provide the first inferential application under the spatial continuum, current work by Guindon et al. (2016) involves an alternative method to estimate similar parameters under the continuum model using an MCMC approach without the torus assumption. These novel approaches are a promising indication of the utility of the continuum model for understanding the spatial dynamics of demographic history underlying population genetic structuring.

Genetic simulation methods that incorporate two-dimensional space are inherently computationally expensive. Our statistical pipeline is a promising first step in overcoming these difficulties, and our results give a strong indication that this will soon be possible. Ideal applications of our method are on semi-continuous as well as spatially and temporally heterogeneous populations where the expected density is low; under these assumptions we expect the method to perform well.

Data archiving

Simulation code is available at https://github.com/tyjo/ABC-Discsim.