Abstract
Theoretically, the dynamics of clonal and genetic diversities of clonal plant populations are strongly influenced by the competition among clones and rate of seedling recruitment, but little empirical assessment has been made of such dynamics through temporal genetic surveys. We aimed to quantify 3 years of evolution in the clonal and genetic composition of Zostera marina meadows, comparing parameters describing clonal architecture and genetic diversity at nine microsatellite markers. Variations in clonal structure revealed a decrease in the evenness of ramet distribution among genets. This illustrates the increasing dominance of some clonal lineages (multilocus lineages, MLLs) in populations. Despite the persistence of these MLLs over time, genetic differentiation was much stronger in time than in space, at the local scale. Contrastingly with the short-term evolution of clonal architecture, the patterns of genetic structure and genetic diversity sensu stricto (that is, heterozygosity and allelic richness) were stable in time. These results suggest the coexistence of (i) a fine grained (at the scale of a 20 × 30 m quadrat) stable core of persistent genets originating from an initial seedling recruitment and developing spatial dominance through clonal elongation; and (ii) a local (at the scale of the meadow) pool of transient genets subjected to annual turnover. This simultaneous occurrence of initial and repeated recruitment strategies highlights the different spatial scales at which distinct evolutionary drivers and mating systems (clonal competition, clonal growth, propagule dispersal and so on) operate to shape the dynamics of populations and the evolution of polymorphism in space and time.
Similar content being viewed by others
Introduction
Clonality is a life history trait widely distributed among taxa and habitats, particularly in photosynthetic organisms. Partially clonal organisms are characterized by a mixed system allowing the combination of two reproductive strategies: the production of new genetically identical modules through vegetative growth or fragmentation and the production of new genetic individuals through sexual recombination. As a consequence, their population dynamics and evolutionary trajectories are profoundly affected by their rate and mode of clonal reproduction. Populations of clonal plants are composed of genetic individuals, or genets occupying space and dispersing locally through the production of modular shoots, or ramets (Harper, 1977). As genets are able to persist through time and space, the composition and evolution of populations of clonal plants is largely affected by the level of intraspecific competition (Eriksson, 1989, 1993; Pan and Price, 2001; Travis and Hester, 2005).
Depending on the turnover of genets and intensity of inter-genet competition for space, two extreme recruitment strategies have been defined (Eriksson, 1993): (i) the ‘Initial Seedling Recruitment’ (ISR) strategy, characterizing populations originating from a single event of colonization from one pool of seeds, followed by occupation of space, mostly through vegetative spread; and (ii) the ‘Repeated Seedling Recruitment’ (RSR) strategy, describing the continuous input of new genets.
In stable environments, ISR is expected to be the predominant strategy. Density-regulated populations are shaped by increasing competition among genets through time, the more ecologically competent excluding the less fit (Eriksson, 1989, 1993). This competitive exclusion among genets may theoretically result in a decrease of clonal richness through time, and is considered to be a major driver of the temporal evolution of clonal diversity (Soane and Watkinson, 1979; Eriksson, 1993; Watkinson and Powell, 1993). Such a strategy is similar to the mechanisms suggested by species coexistence models (Huston, 1979), and was proposed to describe the dynamics of meadows of the seagrass Posidonia oceanica (Arnaud-Haond et al., 2010).
In contrast, a strategy closer to RSR is expected in areas that undergo frequent disturbances (Eriksson, 1993), where ecological events locally remove individuals and free microsites for new recruits. Populations of the seagrass Cymodocea nodosa have been proposed to persist due to an RSR strategy (Ruggiero et al., 2005).
These strategies are two theoretical extremes observed in nature in proportions depending mostly on the species studied, and on the rate and intensity of environmental perturbations and demographic variations (Watkinson and Powell, 1993; Pluess and Stocklin, 2004; Douhovnikoff et al., 2005). Their relative importance has strong implications for the evolution of populations and species, as spatio-temporal recruitment strategy affects both the preferential mechanism of space occupation and migration (clonal spread versus fragment or seed dispersal), and the predominant entity that persists will evolve under natural selection (the alleles or the clonal lineages, see Ayala, 1998). The pattern of spatial distribution of genetic and clonal diversities and their respective evolution in time will therefore be highly dependent on the balance between these two strategies. Numerous spatial studies have been carried out for diverse species, reporting highly variable levels of clonal richness that suggest a differential intensity between ISR and RSR strategies (Escaravage et al., 1998; Coyer et al., 2004; Olsen et al., 2004; Pluess and Stocklin, 2004; Diaz-Almela et al., 2007; Alberto et al., 2008). The extreme and most demonstrative cases of ISR dominance are the monoclonal meadows of some seagrass species, including Z. marina (Reusch et al, 1999; Olsen et al., 2004), C. nodosa (Alberto et al., 2008) or P. oceanica (Arnaud-Haond et al., 2007b, 2012). Meadows of the seagrass Z. marina surveyed simultaneously for their demographic evolution and genetic composition in Brittany were shown to be fluctuating mosaics of genetically differentiated patches with variable levels of genotypic and genetic diversity (Becheler et al., 2010). The clonal and genetic composition of meadows suggested that both ISR and RSR strategies may apply in variable proportions as a function of the time elapsed since the last colonization and of the frequency and extent of disturbances (Becheler et al., 2010). However, the thorough appraisal of the dynamics of these genetic mosaics and of the recruitment strategies operating at different spatial and temporal scales in natural meadows cannot be inferred from a single instantaneous snapshot. Such an approach requires the assessment of the temporal evolution of clonal and genetic composition of patches, an approach that has rarely been used on clonal organisms (see Hossaert-McKey et al., 1996; Cronberg, 2002; Travis and Hester, 2005).
Here, we aimed to provide an estimate of short-term temporal variation in clonal and genetic composition at local and regional scales, in relation to the demographical changes recorded, particularly the time elapsed since the last recorded recolonization or major disturbance event. The seven meadows of Z. marina studied in 2009 were sampled again in 2012, following the same sampling strategy, and each ramet was genotyped using the same nine microsatellite markers. Our objective was to compare the spatial and temporal scales of evolution in clonal diversity and spread versus genetic diversity in order to infer the balance among recruitment strategies in natural meadows.
MaterialS and methods
Sample collection and field observations
Following the same sampling scheme and strategy as in Becheler et al. (2010), sampling units of Z. marina were collected in Spring 2009 and Spring 2012 from seven locations in Brittany, France (Supplementary Figure S1), stretching from Saint-Malo to Arradon. Distances between meadows ranged from 33 km (Molène–Roscanvel) to 442 km (Arradon–Saint-Malo). At each location, two 20 × 30 m quadrats separated by several tens of meters were chosen, which were located in continuous parts of the meadow being monitored by the REBENT survey (www.rebent.org), a national network of survey for major coastal ecosystems. Sampling units, corresponding to one ramet, were collected at 35 random coordinates within each quadrat, and their set of internal leaves were stored in silica crystals until DNA extraction. In Arcouest and Molène, due to patchiness of the meadow, the sampling area was not strictly 30 × 20 m2 because the total area covered by the patches had narrowed to less than this size. Deviation from random coordinate occurred when a gap was found on the field at the pre-identified coordinate (therefore corrected to the one of the closest existing ramet). The quadrat 1 of Arcouest was haphazardly sampled due to harsh meteorological conditions. In general, as only approximate GPS (global positioning system) positions were available together with visual cues, the quadrats for 2012 were placed as close as possible to the quadrat positions in 2009 but might have slightly shifted depending on the extent of the meadow and the moving of sediments. The estimated discrepancy between new and initial positions of quadrats was nevertheless estimated to be relatively weak and unlikely to exceed 10 m, except possibly at the Arcouest site, where the coastal landscape had significantly changed.
Microsatellite amplification and genotyping
Total DNA was extracted using the classic CTAB (cetiltrimetilamina) method (Doyle and Doyle, 1988). Using PCR conditions identical to those used by Becheler et al. (2010), the nine microsatellite loci used in 2009 were amplified in the present study. PCR products were visualized using the same ABI-3100 FNVR automated sequencer (Applied Biosystems, Life Technologies, Saint-Aubin, France), and scored using the microsatellite plugin of Geneious v5.6.4 (Biomatters, Auckland, New Zealand). Double-blind reading was used to minimize the occurrence of scoring errors and verify interpretation of the peaks.
To standardize the samples to the same number of sampling units (n=30) before analyses, incomplete genotypes were removed and excess genotypes were randomly removed.
Genetic and clonal data analysis
The first step of the genetic analyses was the clonal discrimination, based on the probability that identical multilocus genotype (MLG) arise from distinct events of sexual reproduction, as described in Arnaud-Haond et al. (2007a). When Psex(FIS) (estimated taking departure from Hardy–Weinberg into account) falls below a threshold value fixed at 0.01, the two identical MLGs are considered as belonging to the same clonal lineage. The data set was also screened for the possible occurrence of scoring errors and somatic mutations, in order to avoid overestimates of clonal diversity. Multilocus lineages (MLLs) were defined as clustering slightly different MLGs likely belonging to the same genet, as detailed in Arnaud-Haond et al. (2007a) and in the Supplementary Information.
Clonal diversity was estimated with three parameters, previously used in Becheler et al. (2010) and recommended in Arnaud-Haond et al. (2007a), as this set fully describes richness and diversity of the clonal composition. R is the clonal richness, estimated as the ratio of the number of discriminated genets within the sampling set with the number of sampling units (Dorken and Eckert, 2001). The slope (β) of the Pareto distribution, describing the distribution of ramets within genets (see Arnaud-Haond et al., 2007a for details), and sensitive to the presence or absence of dominant clonal lineages is also provided, as well as the Simpson’s Index (Pielou, 1969), an index of diversity sensitive to dominant entities. Clonal discrimination and estimations of the parameters of clonal diversity and structure were performed with Genclone 2.1 (Arnaud-Haond and Belkhir, 2007).
A single copy of each discriminated MLL was retained in the data set used to assess genetic diversity and structure.
Genetic diversity within quadrats was estimated as the mean number of alleles per locus (Â), with observed (HO) and unbiased (HE) multilocus heterozygosity (Nei, 1978). A permutation procedure (1000 permutations) was used to test whether a particular estimate of the overall inbreeding coefficient (FIS) was significantly different from 0 (P<0.01). Genetic structure among samples was estimated with θ (Weir and Cockerham, 1984) for 1000 permutations. This Fst-estimator was used to assess the spatial genetic structure among locations and between quadrats from a single location. In addition, a Mantel test including geographical distances among quadrats was carried out to test for the 2D-Isolation-By-Distance model, crossing the logarithm of the geographical distance (in kilometers) between quadrats and a derived index of genetic differentiation (Fst/(1−Fst)), as recommended by Rousset (1997). For each sampling quadrat, this same estimator of Fst was also used on data sets gathered in 2009 (Becheler et al., 2010) and 2012 (the present study) in order to assess the temporal genetic structure between identical sampling quadrats.
Autocorrelation analyses were also performed to estimate the evolution of the pattern of clonal extension and spatial genetic structure at the within-quadrat level. We used the kinship estimator coefficient of Ritland (1996) (Fij) as a genetic relatedness statistic . We performed regression analyses of mean Fij against the Loge of mean geographic distance within each distance class. The autocorrelation analyses were performed using Fij, first including all sampled ramets and then using permutations (1000) in order to include only one ramet (and one of the possible corresponding coordinates, randomly chosen for each permutation step) from each genet at each permutation, in order to examine the dispersion through sexual propagules. The slopes of regressions (b) allowed us to calculate the Sp-statistic (Vekemans and Hardy, 2004). Autocorrelation parameter estimations were performed with GENCLONE 2.1 (Arnaud-Haond and Belkhir, 2007).
The clonal subrange (CR) was estimated that corresponds to the maximum distance between two identical MLGs belonging to the same clone, in meters, and is determined as the distance for which the probability of clonal identity becomes null (Harada et al., 1997; Alberto et al., 2005). It therefore provides an estimate of the minimal spatial extent of the largest observed clone in each quadrat.
The total number of genotypes occurring in the sampling quadrats in 2009 was approximated as follows: with R, the clonal richness (assessed from analyses), and with Ntot, the total numbers of ramets, within a quadrat (assessed using density counts in three subplots of 0.10 m2 in the quadrat to estimate overall density across the entire surface of 30 * 20 m quadrats, see Arnaud-Haond et al. (2012) for a similar approach):
Gtot=R × Ntot.
This allows an estimate of the expected percentage of each present MLG being sampled %Gsampled, corresponding to the sampling density at the genotypic level:
%Gsampled=(G/Gtot) × 100
G being the number of MLGs detected in our sampling set of 30 ramets. This percentage estimate was used to appraise the likelihood of sampling the same MLG twice (both in 2009 and 2012). If R provides a reliable estimate of clonal richness, such percentage is extremely low, owing to the very low sampling density. Despite such low percentage, the repeated observation of persistent MLG sampled both in 2009 and 2012 suggests an overestimation of clonal richness through R estimates. This would imply the occurrence of a large dominance of space occupation by few clonal lineages, as showed in both seagrass species P. oceanica and C. nodosa, and confirm the consistent overestimation of clonal richness estimates based on extremely low sampling densities as usually performed in clonal plants (Arnaud-Haond et al., 2007a).
Network analysis
Network analysis was performed on the basis of the totality of genets in the data set (n=289) to compare the shape and properties of the networks in 2009 (Becheler et al., 2010) and 2012 (the present work) on both local and regional scales. Nodes in the network represent genets, whereas links represent the genetic distance between two genets.
The genetic distance used is the ‘Shared Allele Distance’ (Chakraborty and Jin, 1993) based on the proportion of shared alleles between two individuals. It is estimated by:

where the number of shared alleles S is summed over all loci u, and nu is the number of loci.
Distance between individuals DSA ranges from 0 to 1:

A ‘fully connected’ network was built, including all links among all genets, and then scanned to the percolation threshold (Stauffer and Aharony, 1994) as previously done for this type of data (Rozenfeld et al., 2007; Becheler et al., 2010; Moalic et al., 2011). This method aims to analyze network topology at the minimal genetic distance, allowing gene flow to spread throughout a giant network. Under the effective percolation distance, a giant network collapses into smaller isolated clusters. Occasionally, when the system is not fully hierarchically structured, several nodes will prematurely disconnect and stand-alone outside of the giant cluster. This happens when genets are particularly genetically distinct (and therefore distant) from all other genets of the system. Only when a secondary cluster emerges, made of several nodes (genets), is the effective percolation threshold reached. The percolation threshold reveals the first significant level of limitations to gene flow within the system. Only links just above the effective percolation distance were used to analyze the topology and features of the network. The clustering coefficient Ci of genet i is the ratio between the number of existing links to the maximal number of potential links within the cluster. The clustering of genets reveals the existence of substructures, grouping the closest genets. It is defined as:

where Ei is the number of links existing among the neighbors of a given genet i, and the degree ki of genet i is the number of other genets linked to it. The clustering coefficient of the whole network 〈CC〉 is defined as the average of all individual clustering coefficients in the system. Topologies and features of the current network were also compared with the network obtained in 2009. In order to visualize finer structures, the same methodology was performed to build a network for each location.
Results
Short timescale variation of clonal diversity and architecture
All replicates of identical MLG showed a significant Psex (P<0.01) supporting the hypothesis they belonged to the same genet, and were therefore issued of a single event of sexual reproduction. In a single instance, two slightly different MLG were found to be likely derived from a single event of reproduction and differed at only one allele as a product either of somatic or of in vitro mutation, both MLG were merged into a single MLL (Arnaud-Haond et al., 2007a) and considered as a single genet for further analysis.
Clonal diversity is variable in time depending on quadrat more than site (Table 1; Figure 1). In 2009, the mean clonal richness R was 0.76 with a variance of 0.03, ranging from 0.48 to 1. In 2012, the mean clonal richness had remained rather steady (0.71) with lower variance (0.01). The least and most diverse quadrats remained the same, respectively, Molène (R2009=0.48; R2012=0.51) and the quadrat 1 of Roscanvel (R2009=1; R2012=0.89). On the overall data set, the mean clonal richness of 2009 and 2012 are not significantly different (Wilcoxon test: W=102; P=0.38).
Diagrams of the temporal evolution of intraspecific diversity, for the observed heterozygosity (Ho), the mean number of alleles (Â), the clonal richness (R) and the β of Pareto’s distribution, for each quadrat. x and y axes represent values from 2009 and 2012, respectively. For each site quadrat 1 is shown by a circle and quadrat 2 by a diamond.
The Simpson Index values, D*, were very stable between 2009 and 2012 (Table 1), and no significant evolution was observed between 2009 and 2012 (Wilcoxon test: W=101.5; P=0.39). Contrastingly, the β-parameter of the Pareto distribution was the most variable of the descriptive parameters estimated (Table 1; Figure 1), and its quasi unidirectional evolution showed a consistent decrease of between 31 and 93% (except in Arcouest, quadrat 1, where there was an increase of 38%). The percentages of variation of β and the CR are highly correlated (R2=0.77; P<0.01; negative slope), indicating that an increase in the size of genets (CR) is related to reduced evenness in the distribution of ramets among genets (reflected by the β-parameter of Pareto). In the overall data set, the mean values of the β-parameter of 2009 and 2012 were significantly different (Wilcoxon test: W=139; P=0.006), indicating a consistent increase in clonal dominance.
In five quadrats of the 13 sampled, despite the possible shift in coordinates between dates and the low sampling densities, common MLGs were found in 2009 and 2012, with all Psex values being <0.001. One to six shared clonal lineages were found in five quadrats (Table 1). Assuming R provided a reliable estimate of genotypic richness (see Arnaud-Haond et al., 2007a), the total number of genotypes expected to occur in each quadrat was estimated to be between 45 900 in Molène and 34 4172 in the quadrat 1 of Saint-Malo, resulting in a sampling coverage of 0.01–0.04% genotypes (Supplementary Table S1).
For most of the locations, the shoot density was found to be relatively stable between 2009 and 2012 (Supplementary Table S2). It should be noted that a full colonization event had happened between 2008 and 2009 in quadrat 2 of Sainte-Marguerite, offering the opportunity to follow the first year of clonal structure evolution, which could have affected the fluctuation in density.
Temporal variation of genetic composition of quadrats
Genetic diversity descriptors showed more stable patterns through time than clonal diversity ones (Table 1; Figure 1). The mean heterozygosity was steady with 0.46 in 2009 and 0.45 in 2012, associated with a constant variance (0.004 in 2009 and 2012). No significant differences in heterozygosity were found between 2009 and 2012 (Wilcoxon test: W=98; P=0.50). Similarly, values of allelic richness of 2012 are not significantly different from values of 2009 (Wilcoxon test: W=104.5; P=0.32).
Spatio-temporal genetic structure and differentiation among and within populations
Results in 2012 were similar to those observed in 2009 at local and regional scales. Spatial genetic structure was observed at all scales (Supplementary Table S3), all Fst-values being significantly different from 0 except between the two sampling quadrats of Arradon. This reveals a strong genetic differentiation on different spatial scales: from the regional scale, where Fst-values vary between 0.01 and 0.35, to the local scale, where the differentiation between the two quadrats produces Fst-values varying from 0 to 0.05. Temporal Fst-values were all significant and were systematically higher than inter-quadrat Fst-values (Table 2) ranging from 0.04 to 0.18.
A Mantel test carried out among all pairs of quadrats was significant (R2=0.06; P<0.05), presenting a pattern very similar to the one observed in 2009. Yet, as explained in Becheler et al. (2010), this cannot indicate a strict IBD pattern, as the hierarchical sampling, resulting in two clouds of dots, drives this apparent tendency (Supplementary Figure S2). No such correlation was observed within each of the clouds corresponding to the pairs of quadrats from the same location (R2=0.03; P=0.73) or to pairs of quadrats among locations (R2=0.001; P=0.71).
Network analysis
The global network topology built on the base of genets in 2012 (Figure 2) was highly similar to the one obtained in 2009, with identical percolation threshold (Dpe=0.45). We observe the same organization with three central locations (Callot, Arcouest and Saint-Malo) and four peripheral ones (Arradon, Roscanvel, Molène and Sainte-Marguerite). The clustering coefficient 〈CC〉 was slightly higher than that recorded in 2009 (0.37 vs 0.30), suggesting an increase in the hierarchical differentiation among clusters (mainly corresponding to sets of samples within each location).
Network topology of the seven meadows of Z. marina based on the Shared Allele Distance between genets. Only links with distances smaller than or equal to the percolation threshold (Dpe=0.45) are presented. For greater readability, nodes representing genets are not arranged according to their geographic coordinates. For each location, genets of quadrat 1 are represented by circles and genets of quadrat 2 by boxes. Colors correspond to sampling locations, according to the legend of Figure 1.
In order to see whether this result was because of an increase in differentiation at the regional or local scale, networks were also constructed at the levels of localities. This analysis also revealed an increase in clustering within every locality except for Saint-Malo (0.43 in 2012 vs 0.52 in 2009). Slight increases of a few percent were observed in Arradon and Roscanvel (+1 and +2%, respectively) and strong increases were observed in Molène and Callot (+34% for both), Sainte-Marguerite (+53%) and Arcouest (+47%). All values of 〈CC〉 are given in the Supplementary Table S4. In addition, no clusters of MLG corresponding to quadrats delineation are observed in 2012, in contrast to what was observed for most of the locations in 2009.
Discussion
The snapshot of spatial genetic structure previously recorded at different scales suggested the existence of temporally fluctuating mosaics of genets shaping patches within meadows (Becheler et al., 2010). This temporal survey aims to confirm this hypothesis. The comparison of clonal architecture and genetic composition between 2009 and 2012 provides insight into the possible dual dynamics of the meadows. First, an increasing dominance of large genets was observed, indicating the existence of a core of stable genets. This contrasts with the strong temporal genetic structure between the 3 years of monitoring, suggesting the concomitant occurrence of a turnover of genets. In the light of the recent demographic history of the quadrats, we propose a scenario explaining the evolution observed.
Prevalence of the ISR strategy: toward the emergence of large clones
Evenness of clonal distribution decreased in the large majority of quadrats (Table 1), whereas the CR showed an overall increase. These points highlight an increased dominance of large MLLs. The large MLLs varied in size, reaching at least 19 m in two quadrats (Table 1), and revealed the persistence of a stable core within the seagrass meadows, implanted for several years or decades, as horizontal rhizome elongation rate for Z. marina is estimated between 22 and 31 cm per year (Marba and Duarte, 1998). In addition, genets that persisted in time were revealed by the resampling of identical genets across a 3-year period. Considering the low density of sampling and the low percentage of genotypes covered by our analysis, repeated sampling of some genets in time implies a rather strong pattern of clonal dominance. This dynamic of persistence and increased dominance of clones competing for space is exemplified by the analysis of quadrats showing stable density after a recent colonization, for example, in Sainte-Marguerite (Q2), where a decrease in clonal richness and evenness of respectively 15 and 49% was accompanied by an almost doubled CR. A very similar scenario occurred in the two quadrats of Callot, where a large increase of density occurred in 2008 (Supplementary Table S2), constituting a potential high input of new genets and leading to an increase in clonal richness for 2009. These elements highlight the prevalence of an ISR strategy (Eriksson, 1993).
A similar study was performed on a meadow of the terrestrial clonal plant Lathyrus sylvestris, studied in 2 successive years (Hossaert-McKey et al., 1996), where a similar pattern of clonal dominance fitted with a predominantly ISR strategy (Figure 3a). In contrast to the present work, a large spatial but low temporal genetic structure was observed and interpreted as the result of successive colonizations at the edge of the population having formed mosaics of genets: (i) colonizing space through vegetative elongation and (ii) producing seedling through reproduction among flowers of the same genet or its relatives, recruiting closed to the maternal plants (Hossaert-McKey, 1988; Hossaert-McKey and Jarry, 1992; Hossaert-McKey et al., 1996).
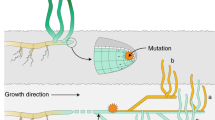
Conceptual illustration of scenarios proposed for explaining the spatio-temporal genetic structure. (a) Representation of the scenario described in Hossaert-McKey et al. (1996). (b) Representation of the scenario proposed in the discussion, which fits better with our results. The dual composition of the meadows (or sampling quadrats) contains cores of persistent genets (blue and green circles) and clouds of transient genets (orange and pale blue layouts, for 2009 and 2012 respectively). The divergence between cores is probably because of difference of genets having colonized both quadrats at the last event of drastic extinction, generating spatial structure. Annual migration and settlement provide pools of transient genets, of short lifespan, generating the temporal structure. In the scenario a, the flow of new genets is weak (weak temporal structure), and colonization of gaps is probably due to clonal elongation and mating among relatives (strong spatial structure). In the scenario b, annual input of transient genets is strong, maximizing the temporal structure.
This pattern bears some similarity to the evolution through time of stable cores of large genets reported here, revealing a strategy of ISR and trimming of genets through the differential capacity of spatial spread and possible intraspecific competition in Z. marina meadows. Under relatively stable demographic conditions, differential clonal spread would therefore have a major role in shaping the clonal composition and differentiation of quadrats separated by only several tens of meters, as previously suggested by Becheler et al. (2010). The temporal component is, however, strikingly different in these two studies, whereas in case of L. sylvestris, the temporal differentiation was less marked than the spatial one, results show the opposite in Z. marina meadows. Such a contrasted pattern may be attributed to the contrasted mechanisms and dynamics of dispersal in the sea compared with on land. This leads us to propose a slightly different scenario (Figure 3b) to explain our findings, taking into account the large dispersal potential of seagrasses through drifting shoots or seeds in the marine environment (Harwell and Orth, 2002; Kendrick et al., 2012).
A cloud of transient genets revealed by the temporal aspect of genetic patchiness
Reported in various marine taxa (Johnson and Black, 1982; Jones et al., 1999; Arnaud-Haond et al., 2008; Selkoe et al., 2010; Hedgecock and Pudovkin, 2011), genetic patchiness is a paradoxical combination of high dispersal potential and strong genetic structure at local scales, characterized by three main features: (i) a fine-grained genetic structure comparable to or apparently exceeding that observed at a large scale; (ii) the fuzziness of population contours; and (iii) rapid temporal variations. The two first criteria were already met in for Z. marina meadows in Brittany (Becheler et al., 2010) as well as in San Francisco Bay (Ort et al., 2012), underlining the importance of clonality in favoring fine-grained genetic structure and spatial patchiness in organisms with mixed mating systems. Here, the temporal genetic structure exceeding the spatial one (Table 2) underlines a rather fast modification of genetic composition of patches, which is in line with the third characteristic describing genetic patchiness. The strong temporal Fst observed in this study emphasize the equal importance of dispersal and settlement of ‘non-dominant clones’, and lead us to hypothesize that a second compartment of genets could exist, subject to turnover within short time periods and generating significant variation in the genetic composition of quadrats through time (temporal Fst, Table 2).
Independent of longer-term meadow stability, the dynamics of Z. marina meadows are punctuated by annual variations in density, with a rather synchronized peak of recruitment of new ramets in early spring, filling gaps left by an annual winter drop in density (Marba et al., 1996). Spring increase in density can be caused by the local clonal spread of genets that have persisted through winter, or new waves of recruits through ramet and seedling dispersal/settlement over broader spatial scales. Although the existence of persistent and widely spread genets reported here supports the first of these possible explanations, the temporal pattern of differentiation also suggests the co-occurrence of the latter. An annual cloud of recruits may disperse in synchronized waves settling over spatial scales encompassing both quadrats, tending to bring quadrats genetically closer. This likely annual turnover of transient genets illustrates the occurrence of a parallel RSR strategy (Eriksson, 1993) in Z. marina meadows. Following a typical pattern of genetic patchiness, the clouds of recruits may originate from a limited pool of plants or patches in the meadow and differ among years, therefore explaining the large temporal differentiation observed among quadrats. A recent work (Broquet et al., 2012) analytically demonstrates that ‘chaotic patchiness can be produced by neutral demographic processes alone’, including collective dispersal (Selkoe et al., 2006) and genetic drift. This is well illustrated by the successive recruitment events proposed to explain the empirical results reported here.
Conclusion
This study provides the first short-term temporal assessment of the dynamics of clonal and genetic composition of seagrass meadows at fine-grained, local and regional scales. Results revealed a typical pattern of genetic patchiness, with small-scale genetic structure despite large-scale dispersal potential, and high temporal differentiation. Some mechanisms underlying this observation appear slightly different from those of other marine species, however, as clonal growth and differential fitness of genets appear, as for terrestrial clonal plants, to be the root of the fine-grained differentiation observed between quadrats within meadows. At fine-grained scale, results support an ISR Strategy and the temporal persistence of part of the genetic pool. We therefore propose a scenario involving two compartments of genets to explain the results reported here (Figure 3b). The first compartment is a core of persistent and growing genets (ISR) contributing to the spatial differentiation within meadows, which may either result from a different time or source of colonization or from genetic divergence through differential exclusion of genets in the distinct quadrats. The second compartment is an annual cloud of transient genets, mostly alternating on an annual basis (RSR); although data reported here does not exclude the possibility that some of those genets would occasionally succeed on the longer term and finally contribute to the persistent core. These scenarios imply a central role on the frequency of perturbations and clonal life history traits, in particular, spatial spread and selection acting on clonal lineages, in the evolution of the clonal and genetic composition of meadows. These observations confirm the ecological concept of population based on distribution continuity as best adapted to clonal plants (Becheler et al., 2010), but suggest the possible existence of a spatial scale larger than sampling sites, and within which allelic frequencies may remain stable in time. These results underline the importance of addressing distinct interlocked spatial and temporal scales simultaneously in order to gain understanding of the dynamics of a population system as a whole. This is particularly important in those seagrass meadows apparently following permanent non-equilibrium dynamics at a local scale, possibly combined with long-term stability at a global scale.
Data archiving
Data deposited in the Dryad repository: doi:10.5061/dryad.1vp70.
References
Alberto F, Gouveia L, Arnaud-Haond S, Perez-Llorens JL, Duarte CM, Serrao EA . (2005). Within-population spatial genetic structure, neighbourhood size and clonal subrange in the seagrass Cymodocea nodosa. Mol. Ecol. 14: 2669–2681.
Alberto F, Massa S, Manent P, Diaz-Almela E, Arnaud-Haond S, Duarte CM et al. (2008). Genetic differentiation and secondary contact zone in the seagrass Cymodocea nodosa across the Mediterranean-Atlantic transition region. J Biogeogr 35: 1279–1294.
Arnaud-Haond S, Belkhir K . (2007). GENCLONE: a computer program to analyse genotypic data, test for clonality and describe spatial clonal organization. Mol Ecol Notes 7: 15–17.
Arnaud-Haond S, Duarte CM, Alberto F, Serrao EA . (2007a). Standardizing methods to address clonality in population studies. Mol Ecol 16: 5115–5139.
Arnaud-Haond S, Duarte CM, Diaz-Almela E, Marba N, Sintes T, Serrao EA . (2012). Implications of Extreme Life Span in Clonal Organisms: Millenary Clones in Meadows of the Threatened Seagrass Posidonia oceanica. Plos One 7: 2.
Arnaud-Haond S, Marba N, Diaz-Almela E, Serrao EA, Duarte CM . (2010). Comparative analysis of stability-genetic diversity in seagrass (Posidonia oceanica) meadows yields unexpected results. Estuaries and Coasts 33: 878–889.
Arnaud-Haond S, Migliaccio M, Diaz-Almela E, Teixeira S, van de Vliet MS, Alberto F et al. (2007b). Vicariance patterns in the Mediterranean Sea: east-west cleavage and low dispersal in the endemic seagrass Posidonia oceanica. J Biogeogr 34: 963–976.
Arnaud-Haond S, Vonau V, Rouxel C, Bonhomme F, Prou J, Goyard E et al. (2008). Genetic structure at different spatial scales in the pearl oyster (Pinctada margaritifera cumingii) in French Polynesian lagoons: beware of sampling strategy and genetic patchiness. Marine Biol 155: 147–157.
Ayala FJ . (1998). Is sex better? Parasites say "no". Proc Natl Acad Sci USA 95: 3346–3348.
Becheler R, Diekmann O, Hily C, Moalic Y, Arnaud-Haond S . (2010). The concept of population in clonal organisms: mosaics of temporally colonized patches are forming highly diverse meadows of Zostera marina in Brittany. Mol Ecol 19: 2394–2407.
Broquet T, Viard F, Yearsley M . (2012). Genetic drift and collective dispersal can result in chaotic genetic patchiness. Evolution 67: 1660–1675.
Chakraborty R, Jin L . (1993). A unified approach to study hypervariable polymorphisms: statistical considerations of determining relatedness and population distances. Exs 67: 153–175.
Coyer JA, Diekmann OE, Serrao EA, Procaccini G, Milchakova N, Pearson GA et al. (2004). Population genetics of dwarf eelgrass Zostera nolti throughout its biogeographic range. Marine Ecol Prog Series 281: 51–62.
Cronberg N . (2002). Colonization dynamics of the clonal moss Hylocomium splendens on islands in a Baltic land uplift area: reproduction, genet distribution and genetic variation. J Ecol 90: 925–935.
Diaz-Almela E, Arnaud-Haond S, Vliet MS, Alvarez E, Marba N, Duarte CM et al. (2007). Feed-backs between genetic structure and perturbation-driven decline in seagrass (Posidonia oceanica) meadows. Conserv Genet 8: 1377–1391.
Dorken ME, Eckert CG . (2001). Severely reduced sexual reproduction in northern populations of a clonal plant, Decodon verticillatus (Lythraceae). J Ecol 89: 339–350.
Douhovnikoff V, McBride JR, Dodd RS . (2005). Salix exigua clonal growth and population dynamics in relation to disturbance regime variation. Ecology 86: 446–452.
Doyle JJ, Doyle JL . (1988). Natural interspecific hybridization in eastern north-american Claytonia. Am J Bot 75: 1238–1246.
Eriksson O . (1989). Seedling dynamics and life histories in clonal plants. Oikos 55: 231–238.
Eriksson O . (1993). Dynamics of genets in clonal plants. Trends Ecol Evol 8: 313–316.
Escaravage N, Questiau S, Pornon A, Doche B, Taberlet P . (1998). Clonal diversity in a Rhododendron ferrugineum L. (Ericaceae) population inferred from AFLP markers. Mol Ecol 7: 975–982.
Harada Y, Kawano S, Iwasa Y . (1997). Probability of clonal identity: inferring the relative success of sexual versus clonal reproduction from spatial genetic patterns. J Ecol 85: 591–600.
Harper JL . (1977) Population Biology of Plants. Academic Press: London, UK.
Harwell MC, Orth RJ . (2002). Long-distance dispersal potential in a marine macrophyte. Ecology 83: 3319–3330.
Hedgecock D, Pudovkin AI . (2011). Sweepstake reproductive success in highly fecund fish and shellfish: a review and commentary. Bull Marine Sci 87: 971–1002.
Hossaert-McKey M . (1988) Des fleurs comment et à quoi bon! Données et réflexions sur la reproduction de deux espèces affines à reproduction végétative: Lathyrus latifolius et Lathyrus sylvestris (Légumineuses: Papilionaceae). PhD diss Université Pau: France.
Hossaert-McKey M, Jarry M . (1992). Spatial and temporal patterns of investment in growth and sexual reproduction in 2 stoloniferous species, Lathyrus latifolius and L. sylvestris. J Ecol 80: 555–565.
Hossaert-McKey M, Valero M, Magda D, Jarry M, Cuguen J, Vernet P . (1996). The evolving genetic history of a population of Lathyrus sylvestris: evidence from temporal and spatial genetic structure. Evolution 50: 1808–1821.
Huston M . (1979). General hypothesis of species-diversity. Am Nat 113: 81–101.
Johnson MS, Black R . (1982). Chaotic genetic patchiness in an inter-tidal limpet, Siphonaria sp. Marine Biol 70: 157–164.
Jones GP, Milicich MJ, Emslie MJ, Lunow C . (1999). Self-recruitment in a coral reef fish population. Nature 402: 802–804.
Kendrick GA, Waycott M, Carruthers TJB, Cambridge ML, Hovey R, Krauss SL et al. (2012). The central role of dispersal in the maintenance and persistence of seagrass populations. Bioscience 62: 56–65.
Marba N, Cebrian J, Enriquez S, Duarte CM . (1996). Growth patterns of western Mediterranean seagrasses: Species-specific responses to seasonal forcing. Marine Ecol Prog Series 133: 203–215.
Marba N, Duarte CM . (1998). Rhizome elongation and seagrass clonal growth. Marine Ecol Prog Series 174: 269–280.
Moalic Y, Arnaud-Haond S, Perrin C, Pearson GA, Serrao EA . (2011). Travelling in time with networks: Revealing present day hybridization versus ancestral polymorphism between two species of brown algae, Fucus vesiculosus and F. spiralis. BMC Evol Biol 11: 33.
Nei M . (1978). Estimation of average heterozygosity and genetic distance from small number of individuals. Genetics 89: 583–590.
Olsen JL, Stam WT, Coyer JA, Reusch TBH, Billingham M, Bostrom C et al. (2004). North Atlantic phylogeography and large-scale population differentiation of the seagrass Zostera marina L. Mol Ecol 13: 1923–1941.
Ort BS, Cohen CS, Boyer KE, Wyllie-Echeverria S . (2012). Population structure and genetic diversity among eelgrass (Zostera marina) beds and depths in San Francisco Bay. J Heredity 103: 533–546.
Pan JJ, Price JS . (2001). Fitness and evolution in clonal plants: the impact of clonal growth. Evol Ecol 15: 583–600.
Pielou E . (1969) An Introduction to Mathematical Ecology. Wiley-Interscience: New York, NY, USA.
Pluess AR, Stocklin J . (2004). Population genetic diversity of the clonal plant Geum reptans (Rosaceae) in the Swiss Alps. Am J Bot 91: 2013–2021.
Reusch TBH, Bostrom C, Stam WT, Olsen JL . (1999). An ancient eelgrass clone in the Baltic. Marine Ecol Prog Series 183: 301–304.
Ritland K . (1996). Estimators for pairwise relatedness and individual inbreeding coefficients. Genet Res 67: 175–185.
Rousset F . (1997). Genetic differentiation and estimation of gene flow from F-statistics under isolation by distance. Genetics 145: 1219–1228.
Rozenfeld AF, Arnaud-Haond S, Hernandez-Garcia E, Eguiluz VM, Matias MA, Serrao E et al. (2007). Spectrum of genetic diversity and networks of clonal organisms. J R Soc Interface 4: 1093–1102.
Ruggiero MV, Capone S, Pirozzi P, Reusch TBH, Procaccini G . (2005). Mating system and clonal architecture: a comparative study in two marine angiosperms. Evol Ecol 19: 487–499.
Selkoe KA, Gaines SD, Caselle JE, Warner RR . (2006). Current shifts and kin aggregation explain genetic patchiness in fish recruits. Ecology 87: 3082–3094.
Selkoe KA, Watson JR, White C, Ben Horin T, Iacchei M, Mitarai S et al. (2010). Taking the chaos out of genetic patchiness: seascape genetics reveals ecological and oceanographic drivers of genetic patterns in three temperate reef species. Mol Ecol 19: 3708–3726.
Soane ID, Watkinson AR . (1979). Clonal variation in populations of Ranunculus repens. New Phytol 82: 557–573.
Stauffer D, Aharony A . (1994) Introduction to Percolation Theory Taylor & Francis, London.
Travis SE, Hester MW . (2005). A space-for-time substitution reveals the long-term decline in genotypic diversity of a widespread salt marsh plant, Spartina alterniflora, over a span of 1500 years. J Ecol 93: 417–430.
Vekemans X, Hardy OJ . (2004). New insights from fine-scale spatial genetic structure analyses in plant populations. Mol Ecol 13: 921–935.
Watkinson AR, Powell JC . (1993). Seedling recruitment and the maintenance of clonal diversity in plant populations - a computer simulation of Ranunculus repens. J Ecol 81: 707–717.
Weir BS, Cockerham CC . (1984). Estimating F-statistics for the analysis of population-structure. Evolution 38: 1358–1370.
Acknowledgements
We are deeply grateful to Sara Teixeira, Christophe Bayle and Olivier Mouchel for their pratical help. We also wish to thank the technicians of KerIschia for their help with the field work in Molène; and Vincent Guilbaud for his logistic help during the storage processing of samples. We also wish to acknowledge the two anonymous reviewers and the editor whose comments and suggestions considerably improve the manuscript; and Helen Mc Combie for professional English editing. This work was supported by the ANR-11-BSV7-007 Clonix.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies this paper on Heredity website
Supplementary information
Rights and permissions
About this article
Cite this article
Becheler, R., Benkara, E., Moalic, Y. et al. Scaling of processes shaping the clonal dynamics and genetic mosaic of seagrasses through temporal genetic monitoring. Heredity 112, 114–121 (2014). https://doi.org/10.1038/hdy.2013.82
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/hdy.2013.82
Keywords
This article is cited by
-
The Dynamics of Seagrass Ecosystems: History, Past Accomplishments, and Future Prospects
Estuaries and Coasts (2023)
-
Linking Spatial Patterns of Adult and Seed Diversity Across the Depth Gradient in the Seagrass Zostera marina L.
Estuaries and Coasts (2021)
-
Abiotic and Biotic Interactions Control Ruppia maritima Life History Development Within a Heterogeneous Coastal Landscape
Estuaries and Coasts (2021)
-
Genetic diversity of Halodule wrightii is resistant to large scale dieback: a case study from the Indian River Lagoon
Conservation Genetics (2019)
-
High clonal propagation and low population connectivity in the holothurian Stichopus chloronotus from the Indo-Pacific
Marine Biology (2019)