Abstract
Increasing acceptance that evolution can be ‘rapid’ (or ‘contemporary’) has generated growing interest in the consequences for ecology. The genetics and genomics of these ‘eco-evolutionary dynamics’ will be—to a large extent—the genetics and genomics of organismal phenotypes. In the hope of stimulating research in this area, I review empirical data from natural populations and draw the following conclusions. (1) Considerable additive genetic variance is present for most traits in most populations. (2) Trait correlations do not consistently oppose selection. (3) Adaptive differences between populations often involve dominance and epistasis. (4) Most adaptation is the result of genes of small-to-modest effect, although (5) some genes certainly have larger effects than the others. (6) Adaptation by independent lineages to similar environments is mostly driven by different alleles/genes. (7) Adaptation to new environments is mostly driven by standing genetic variation, although new mutations can be important in some instances. (8) Adaptation is driven by both structural and regulatory genetic variation, with recent studies emphasizing the latter. (9) The ecological effects of organisms, considered as extended phenotypes, are often heritable. Overall, the study of eco-evolutionary dynamics will benefit from perspectives and approaches that emphasize standing genetic variation in many genes of small-to-modest effect acting across multiple traits and that analyze overall adaptation or ‘fitness’. In addition, increasing attention should be paid to dominance, epistasis and regulatory variation.
Similar content being viewed by others
Introduction
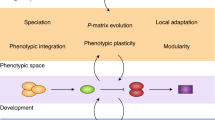
It is now known that ecological change can generate substantial adaptive evolution on very short time scales, such as years or decades (Hendry and Kinnison, 1999; Reznick and Ghalambor, 2001). This realization that evolution can be ‘rapid’ or ‘contemporary’ has generated considerable interest in the possible consequences for ecological dynamics (Thompson, 1998; Hairston et al., 2005; Fussmann et al., 2007; Kinnison and Hairston, 2007; Pelletier et al., 2009; Matthews et al., 2011; Schoener, 2011). In essence, evolution might be altering—almost in real time—the key parameters that ecologists monitor in natural systems. A few examples will serve to illustrate. At the population level, adaptive evolution on a generation-by-generation time scale can substantially alter population size and growth rate (Saccheri and Hanski, 2006; Kinnison and Hairston, 2007; Bell and Gonzalez, 2011; Hanski et al., 2011). At the community level, intraspecific variation in hosts (e.g., trees) or predators (e.g., fish) can influence arthropod communities (Fussmann et al., 2007; Hughes et al., 2008; Johnson et al., 2009; Bassar et al., 2012). At the ecosystem level, intraspecific variation in these same systems can influence primary productivity, decomposition rates and nutrient cycling (Whitham et al., 2006; Bailey, et al., 2009b; Bassar et al., 2012). Moreover, it is increasingly apparent that ecology and evolution can reciprocally influence each other through a variety of feedbacks, such as when an ecological parameter influences the evolution of a trait that influences the same ecological parameter (Post and Palkovacs, 2009). These various interactions between ecology and evolution—acting in either direction—represent the rapidly growing integrated research field now called eco-evolutionary dynamics (Figure 1).
A conceptual diagram outlining the basic elements of eco-evolutionary dynamics. Phenotypic traits in a focal species can influence the population dynamics of that species, which can then influence the structure of the community in which that species is embedded, as well as the functioning of the overall ecosystem. In addition, phenotypic traits in the focal species can directly (that is, not through population dynamics) influence community structure and ecosystem function. Ecological effects at the population, community, and ecosystems levels can then feedback through plasticity or selection to influence phenotypic traits. These phenotypic changes will be passed on to the next generation to the extent that they are genetically based. A previous version of this figure appears in Bailey et al. (2009a).
Phenotypes are the nexus of eco-evolutionary dynamics. First, selection acts directly on phenotypes, whereas it acts only indirectly on genotypes through their association with phenotypes. Any role for ecology in shaping evolution must therefore work through phenotypes. Second, the ecological effects of organisms are mediated through their phenotypes, whereas genotypes have ecological effects only indirectly through their association with phenotypes. Any role for evolution in shaping ecology must therefore also work through phenotypes. For these reasons, an understanding of eco-evolutionary dynamics must come from the study of phenotypes. Phenotypes can be influenced by a variety of effects, including plasticity (and maternal effects), genetic change and their interaction (for example, the evolution of plasticity). Disentangling contributions from these different effects is important, because they are expected to show different patterns, and to manifest different rates, limits and costs (Lynch and Walsh, 1998; West Eberhard, 2003). To date, however, most eco-evolutionary studies have examined effects without evaluating their genetic and plastic basis. As one example, experiments using mesocosms to quantify the effects of fish ecotypes on community and ecosystem variables have thus far used only wild-caught fish (Harmon et al., 2009; Palkovacs and Post, 2009; Bassar et al., 2012), for which genetic and plastic effects cannot be separated. As another example, studies examining the effects of plant genotypes on community and ecosystem variables (Hughes et al., 2008) have often (although not always) chosen genotypes based on neutral genetic variation rather than genetic variation in relevant phenotypes. The present paper was motivated by these limitations, and is written in anticipation of eco-evolutionary studies moving toward an increasingly genetic—and genomic—perspective.
Many reviews have been written on the genetics of adaptation (Orr, 2005; Hoekstra and Coyne, 2007; Barrett and Schluter, 2008; Stern and Orgogozo, 2008; Barrett and Hendry, 2012; Olson-Manning et al., 2012; Rockman, 2012), and these are certainly relevant to eco-evolutionary dynamics. Here, however, I combine and emphasize several elements that set the present review apart from those previous. First, my explicit focus is on phenotypes, for the reasons discussed above. In short, the genetics and genomics of eco-evolutionary dynamics will be—in the main—the genetics and genomics of phenotypic adaptation. Second, I lean as much as possible on data from natural populations. Although theoretical and laboratory studies are also informative, and will be referred to, they will not be representative of nature. Third, I emphasize, whenever possible, the results of meta-analyses, as opposed to specific examples. Examples (especially from threespine stickleback, Gasterosteus aculeatus) will still be provided—and will sometimes be all that is available—but generality ultimately must come from integration across studies, which is the strength of meta-analysis. By the end, I hope to have provided eco-evolutionary practitioners with a useful starting point for integrating genetic and genomic thinking into their research.
Methods for analysis
Methods for studying the genetics and genomics of adaptation are diverse and constantly changing. I here provide only the briefest summary to introduce methods referred to later and to provide references for further information. (1) Quantitative genetics uses artificial or natural crosses to statistically partition phenotypic variance into different components: additive genetic, dominance, epistasis, maternal effects and environmental effects (Falconer and Mackay, 1996; Roff, 1997; Lynch and Walsh, 1998). (2) Linkage mapping normally uses F2 hybrids to test for statistical associations between alleles at marker loci and trait values for phenotypes (Lynch and Walsh, 1998; Rogers et al., 2012). (3) Association mapping is similar to linkage mapping but uses natural variation within or among populations (Buerkle and Lexer, 2008; Kruglyak, 2008; Flint and Mackay, 2009). (4) Genome scans use population samples to measure genetic differentiation at many loci, often with the goal of detecting loci under divergent selection, which are assumed to be high-differentiation outliers (Stinchcombe and Hoekstra, 2008; Nosil et al., 2009). (5) Gene expression studies commonly test for the upregulation or downregulation of genes between populations in similar environments (genetic differences in expression) or between environments for a given population (environmental influences on expression) (Gilad et al., 2009; Pavey et al., 2010). (6) Candidate gene studies determine the extent to which genes of known effect contribute to phenotypic variation within or between populations (Stinchcombe and Hoekstra, 2008). These different methods have different utilities, strengths and weakness, that have been discussed extensively (Lynch and Walsh, 1998; Buerkle and Lexer, 2008; Stinchcombe and Hoekstra, 2008; Mackay et al., 2009; Stapley et al., 2010; Rockman, 2012).
Key questions
In the remainder of this paper, I focus on key questions surrounding the genetics and genomics of phenotypic adaptation—and therefore eco-evolutionary dynamics. The specific questions were chosen because they are much discussed and because their answers are not always obvious. After summarizing empirical data pertaining to each question, I provide a tentative answer. The answers are my own and will not necessarily fall in line with those that other authors might advance, a disagreement that will hopefully stimulate further debate and research.
Question 1: How much genetic variation is out there?
The evolution of phenotypic traits will be heavily influenced by the amount of additive genetic variation—so how much of it is out there? The classic review is the survey by Mousseau and Roff (1987) of narrow-sense heritabilities (ratio of additive genetic variance to total phenotypic variance) in wild, outbred animal populations. Based on 1120 estimates from the literature, the authors calculated mean heritabilities of 0.46 for morphological traits, 0.26 for life history traits and 0.30 for behavioral traits. Figure 2 shows comparable results from a more recent survey by Hansen et al. (2011). Compilations of this sort universally show that most traits in most populations of most species show substantial evolutionary potential. For example, multiplying the median absolute value of bias-corrected selection gradients for morphology (0.15: Hereford et al., 2004) by the median heritability (0.43) yields an expected evolutionary response of 0.065 standard deviations per generation. If sustained, this response would shift the mean trait value by one standard deviation in only 16 generations.
Frequency distribution of 901 narrow-sense heritability estimates compiled by Hansen et al. (2011). All estimates less than zero are included in the first column and all estimates greater than one are included in the last column. Note that although other compilations have more heritability estimates than are reported here, the set shown is the same as that for which for which ‘evolvabilities’ are shown in Figure 3. Regardless, the distribution looks roughly the same in all such data compilations.
An alternative measure of evolutionary potential is the so-called ‘evolvability’—additive genetic variance divided by the square of the mean trait value (Houle, 1992; Hansen et al., 2011). Multiplying an estimate of evolvability by a mean-standardized selection gradient (Hereford et al., 2004; Matsumura et al., 2012) then gives the expected proportional change in the mean trait value per generation. Hansen et al. (2011) reviewed 1465 estimates of evolvability and found that the median value was 0.26; a subset of these estimates is shown in Figure 3. Multiplying this estimate by the median bias-corrected mean-standardized selection gradient in natural populations (0.28: Hereford et al. 2004) yields an expected 0.073% per-generation change in mean trait value. If sustained, this response would shift the mean trait value by 5% in 68 generations.
Frequency distribution of 901 ‘evolvability’ (mean-scaled additive genetic variance) estimates compiled by Hansen et al. (2011). All estimates less than zero are included in the first column and all estimates greater than 100% are included in the last column. Note that I here only show evolvability estimates that correspond to the same studies/traits as those for which narrow-sense heritabilities were reported in Figure 2.
The main message here is simply that evolutionary potential—whatever the metric—is high for most traits in most populations, but the qualifier ‘most’ is critical. For instance, Hoffmann et al. (2003) reported that dessication resistance, an important fitness-related trait influencing adaptation and species distributions in insects, showed zero heritability and zero additive genetic variance in a rainforest population of Drosophila birchii. Kellermann et al. (2006) then showed that this finding generalized to other populations of D. birchii—although other traits in the same populations were not so limited. Finally, Kellermann et al. (2009) showed that several other Drosophila species also lacked heritability and additive genetic variance for dessication resistance. In particular, specialist rainforest species have lost most of the genetic variation in dessication resistance. Although these are perhaps the best-known instances of low heritable variation in natural populations, other studies have reported analogous situations (Bradshaw and McNeilly, 1991; Futuyma et al., 1995).
Answer: Most populations of most species harbor substantial additive genetic variance in fitness-related traits, and therefore should be able to evolve when exposed to altered selection pressures. However, the amount of this variation differs among populations and species, such that the rate of evolution in response to a given selective pressure will be highly variable.
Question 2: To what extent will genetic correlations constrain responses to selection?
The previous answer presumed independent traits whose evolutionary potential can be assessed by reference to genetic variance for a single trait by itself. The reality, however, is that traits can be genetically correlated owing to epistatic interactions between genes, genes with pleiotropic effects, or linkage disequilibrium between alleles at loci affecting different traits (Lynch and Walsh, 1998). Some authors have argued that such correlations can substantially constrain evolution in response to selection (Blows and Hoffmann, 2005; Hansen and Houle, 2008; Kirkpatrick, 2009; Walsh and Blows, 2009).
Meta-analyses reveal frequent, and sometimes strong, genetic correlations among traits (Roff, 1996), suggesting the potential for substantial impacts on evolutionary trajectories. Whether or not these correlations impede evolution depends on how much genetic variation is present in the multivariate direction of selection (Hellmann and Pinedakrch, 2007; Hansen and Houle, 2008; Agrawal and Stinchcombe, 2009; Kirkpatrick, 2009; Walsh and Blows, 2009). Stated another way, we need to know how well the multivariate vector of selection lines up with the multivariate axis of genetic variation. Agrawal and Stinchcombe (2009) addressed this question by surveying studies that measured genetic or phenotypic (co)variances among traits, as well as selection acting on those traits. They then estimated the rate of adaptation (increase in mean fitness) in the presence of the measured correlations relative to their absence. The upshot was that genetic correlations among traits were sometimes expected to influence the rate of adaptation, and this influence was as frequently positive (speeds adaptation) as it was negative (slows adaptation) (Figure 4). The reason trait correlations would often aid evolution was that the axis of selection was often aligned with a major axis of genetic variation.
Frequency distribution of estimates of the extent to which trait correlations are expected to bias the response to selection; based on the meta-analysis of Agrawal and Stinchcombe (2009). x axis values are the log of the ratio of the rate of adaptation (increase in fitness) accounting for trait correlations to the rate not accounting for those correlations. Negative values indicate situations where correlations should constrain the rate of evolution and positive values indicate situations where correlations should increase the rate of adaptation.
The above analyses consider trait correlations on a pair-wise basis, whereas we would ideally consider the n-dimensional multivariate space representing all traits (Bürger, 1986; Blows and Hoffmann, 2005; Hansen and Houle, 2008; Kirkpatrick, 2009; Walsh and Blows, 2009). One approach to this problem is to measure the matrix of additive genetic (co)variances for traits, and to then use the resulting G matrix to estimate the number of effectively independent trait dimensions that could respond to selection (eigenvectors or principal components of the matrix). Some studies adopting this approach have reported only a few effective trait dimensions, which argues that trait correlations could substantially constrain adaptive evolution (Kirkpatrick, 2009; Walsh and Blows, 2009). Other studies, however, suggest that the number of dimensions can be reasonably high (Mezey and Houle, 2005). It seems to me that the number of dimensions usually will be very high, certainly much higher than suggested by the current analyses of suites of very similar traits, such as cuticular hydrocarbons (Blows et al., 2004) or wing shape (Mezey and Houle, 2005; McGuigan and Blows, 2007). The reason is that overall adaptation to a given environment will inevitably involve a host of morphological, life history, physiological and behavioral changes, which will not collapse down to only a few dimensions.
Answer: Genetic correlations can cause evolutionary constraints that slow the rate of adaptation—but such constraints are not universal and might not be even common. I suggest that patterns of genetic variation probably do not cause overwhelming constraints on adaptation in most instances.
Question 3: What about non-additive variation?
I have thus far focused on additive genetic variation, because it allows a relatively straightforward interpretation for how selection should influence phenotypic evolution. However, this focus begs the question: to what extent is evolution driven by additive genetic effects, as opposed to dominance or epistasis (Roff and Emerson, 2006; Hill et al., 2008; Phillips, 2008)? This question is important because non-additive effects can substantially alter evolutionary trajectories, as well as the magnitude and effects of gene flow (Wolf et al., 2000; Wade, 2002).
Work on soapberry bugs (Jadera heamatoloma) adapting to different host plants provides a concrete example of non-additive effects and how quickly they can contribute to adaptation. Specifically, the genetic basis of trait differences between two recently (<100 generations) diverged host races was examined by performing line cross analyses that compared mean phenotypes of parental types, F1 and F2 hybrids, and backcrosses (Carroll et al., 2001, 2003, 2007). Results differed among traits, ranging from almost perfect additivity for host plant preference to a diverse range of dominance and epistatic effects for other traits—and these effects depended on the rearing environment (plant type). Interestingly, dominance appears important between host races of phytophagous insects in general, particularly with respect to performance on the different hosts (Matsubayashi et al., 2010). Mixtures of additive and non-additive effects on adaptive divergence also have been described for many other groups, such as lake versus stream threespine stickleback (Berner et al., 2011) and dwarf versus normal lake whitefish (Coregonus clupeaformis) (Renaut et al., 2009; Bernatchez et al., 2010). Beyond these specific examples, the potential generality of non-additive effects was considered by Roff and Emerson (2006) in their meta-analysis of line cross analyses. They found that dominance made a significant contribution to population differentiation in nearly all cases: 96.5% of life history traits and 97.4% of morphological traits—and the effects were large: the ratio of dominance to additive effects was 1.57 for life history traits and 1.28 for morphological traits. Epistasis was also common, contributing to 79.4% of life history traits and 67.1% of morphological traits. Seemingly in contrast to the above line cross analyses between distinct groups (inbred lines, populations and species), genetic variation within groups has been argued to be predominantly additive (Hill et al., 2008). It remains to be seen whether or not this is a real difference and, if so, what is the reason.
Answer: Evolutionary adaptation, including on contemporary time scales, usually involves both additive and non-additive genetic changes. Theoretical and empirical studies should be expanded to facilitate better consideration and integration of these different—and probably interacting—effects.
Question 4: Many small or few large?
This question is a classic one, dating all the way back to the debates between ‘biometricians’ and ‘Mendelians’ (review: Provine 1971). These two schools of thought were successfully merged during the modern synthesis when it became clear that even polygenic traits were based on Mendelian genes, but the question remained open as to just how many genes of what effect size were important in shaping phenotypes. Classic analyses continued to reveal an apparently dichotomy. On one hand, many continuous traits, such as body size, clearly involve many genes of small effect. On the other hand, many discrete traits, going all the way back to Mendel’s peas, clearly have a single-gene basis. I here ask how these alternatives have fared in the modern era of genomics. At first glance, evidence might seem to be growing for the importance of large-effect genes, given the many recent high-profile examples (see below), but I will use three points to argue that most adaptation is the result many genes of small-to-modest effect.
First, current genomic methods are strongly biased against genes of small effect. This bias is particularly obvious in candidate gene approaches, which deliberately target just the opposite. A strong bias is also present in linkage and association mapping, where estimation problems arise when relevant alleles are found at low frequency, when not enough recombination has occurred to break up large linkage blocks, when the number of individuals is few, when the number of loci is few, when the effect size of alleles is small, and from the need to assume a high threshold effect size to reduce study-wide type-I errors (Buerkle and Lexer, 2008; Mackay et al., 2009). The aggregate extent of these biases can be illustrated by reference to the so-called ‘missing heritability paradox,’ in which genome-wide association studies can explain very little of the heritable variation in most human traits (Mackay et al., 2009; Manolio et al., 2009; Hill, 2010). To address this problem, Yang et al. (2010) estimated the proportion of variance in human height explained by 294 831 single-nucleotide polymorphisms genotyped on 3925 unrelated individuals. Using a novel approach, the authors found that 88% of the variation due to single-nucleotide polymorphisms had been undetected in previous genome-wide association studies because ‘the effects of the single-nucleotide polymorphisms are too small to be statistically significant’ (Yang et al., 2010). A scarcity of genes of large effect also appears to be the case for many other human traits, including susceptibility to diseases (Manolio et al., 2009). In addition, artificial selection studies clearly show that evolutionary changes are often driven by many genes (Hill and Kirkpatrick, 2010), with classic examples including oil and protein content in maize (Zea mays) (Moose et al., 2004) and body weight in chickens (Gallus gallus domesticus) (Johansson et al., 2010).
Second, nearly all studies have sought to explain variance in specific traits, rather than overall adaptation (or ‘fitness’). This distinction is critical because overall adaptation to a given environment will be influenced by many traits. As a result, even the genes explaining high levels of variation in a particular trait might contribute little to overall fitness differences. For example, studies in freshwater versus marine stickleback of the genes EDA (lateral plates) and Pitx1 (pelvis) are often cited as evidence that adaptation is influenced by few genes of large effect. However, three points need to be kept in mind. First, these genes/traits are exceptions, with most other stickleback traits having no single quantitative trait locus (QTL) that explains >50% of the variance (Peichel et al., 2001; Albert et al., 2008; Rogers et al., 2012). This rarity of large-effect genes seems to be general: a meta-analysis of effect sizes in QTL studies comparing phenotypically divergent populations found that the most important QTL typically explained only 14.4% of the variation (Morjan and Rieseberg, 2004). Second, freshwater and marine stickleback differ not only in lateral plates and pelvic structures but also in many other traits, with a partial listing including body size, gill raker number and length, dorsal and anal fin rays, body color, jaw size, spine length, salinity tolerance, swimming performance, reproductive behavior and cold tolerance. Although single (or closely linked) genes might well have effects on several of these traits (Albert et al., 2008; Barrett et al., 2008; Kitano et al., 2010), the great diversity of traits is likely to involve a great diversity of genes. I expect this phenomenon—many traits, and so many genes, are involved in adaptation—to be general across organisms and environments.
Third, genome scans typically reveal that high-differentiation outliers, presumably influenced by divergent selection, represent 5–10% of the genome—and the distribution of these loci clearly implicates multiple unlinked genes (Nosil et al., 2009). To continue with stickleback, Hohenlohe et al. (2010) examined 45 000 single-nucleotide polymorphisms in each of 100 individuals from each of two marine and three freshwater populations. The authors found nine outlier genomic regions that showed elevated divergence in all marine versus freshwater comparisons—and so a minimum of nine genes must be involved. The actual number of genes, however, will be much higher, because (1) multiple genes are present in each genomic region and (2) the focus was only on regions showing parallel divergence across all comparisons. Not surprisingly, then, other work has found many more genes that differ between freshwater and marine stickleback (Shimada et al., 2010; Jones et al., 2012b), and similar results have been obtained for lake versus stream stickleback (Roesti et al., 2012), benthic versus limnetic stickleback (Jones et al., 2012a), and dwarf versus normal whitefish (Renaut et al., 2011). In short, genome scans typically implicate divergence in many genes; and yet these scans still remain biased against genes of small effect. Indeed, other approaches, such as reciprocal transplants and correlations with environmental variables, typically reveal many more loci under selection (Michel et al., 2010; Fournier-Level et al., 2011; Hancock et al., 2011).
Answer: Although variation in some traits is clearly influenced by genes of large effect, the conclusion emerging from genomic studies is that adaptation to a given environment will generally involve many genes of small-to-modest effect (see also Roff, 1997; Flint and Mackay, 2009; Hill, 2010; Rockman, 2012). Current methods are poorly positioned to detect all, or even a substantial fraction, of these genes. Plummeting sequencing costs will allow much larger sample sizes that will increase statistical power and reduce (but not eliminate) these problems, but more sensitive analytical methods also need to be developed. In addition, more studies should examine the genetic basis of overall adaptation (fitness), which integrates across all relevant phenotypic traits. Such studies are critical because many of the phenotypes under selection are not known and may be ‘invisible’ to investigators.
Question 5: What is the distribution of effect sizes?
Even if we now can be confident that adaptation usually involves many genes of small-to-modest effect, the specific number of genes and their effect size distribution remains an open question. (Fisher, 1930; Orr, 1999, 2005). One possibility is the ‘infinitesimal model,’ where—stated in realistic form (Rockman, 2012)—many genes are involved and all are of very small effect. Another is the ‘geometric model,’ which predicts an exponential distribution ranging from many loci with small effects to a few loci with large effects. After accounting for the difficulty of detecting loci of very small effect (as described above), the geometric model predicts a gamma distribution of effect sizes with a shape parameter greater than unity (Otto and Jones, 2000).
Albert et al. (2008) explicitly tested the above alternatives through a QTL mapping study that compared the body shape of marine stickleback from Japan to that of derived freshwater benthic stickleback from Paxton Lake, British Columbia. The authors found that effects of particular QTLs on the morphological difference between the populations approximately followed a gamma distribution—consistent with the geometric model. The largest effect QTL explained ∼22% of the difference, showing yet again that most of the variation is due to genes of small-to-modest effect. The mapping cross in this study was between two very different populations found on opposite sides of the Pacific, and it involved only a single family. The first point is of concern because the differences do not reflect a true ancestor-descendent scenario, although marine populations are often considered nearly panmictic across their range. The second point is of concern because it can miss differences that are not fixed between the populations, and so will underestimate the number of genes involved in adaptation, particularly those of small effect.
Rogers et al. (2012) considered the same topic in the same study system but avoided some of the above concerns by crossing stickleback from a marine population to stickleback from each of four nearby lake populations (although only a single cross was performed in each case). Of additional interest, the phenotypic optimum for stickleback was expected to be farther from the ancestral marine form in two lakes (Cranby and Hoggan) that lacked a predator (prickly sculpin, Cottus asper) versus two lakes (Graham and Paq) that had the predator. The resulting difference in the expected magnitude of adaptive evolution (greater for the former two lakes) allowed testing another of the geometric model’s predictions: larger mutations should contribute when adaptation is to more distant fitness peaks. The authors found that (1) most genes were again of small effect (only three QTL explained >20% of the variation in particular landmark coordinates) and (2) the lake populations adapting to the more distant fitness peak were more likely to have the larger effect QTL (two of the above three QTL were in Cranby Lake and one was in Hoggan Lake) (Figure 5).
Frequency distributions of QTL effect sizes in crosses between marine stickleback from the Little Campbell River (British Columbia, Canada) and freshwater stickleback from each of four lakes in the same region (Rogers et al., 2012). Lakes Graham and Paq also contain predatory sculpins, whereas lakes Cranby and Hoggan do not. The latter lakes are therefore expected to present a phenotypic optimum for stickleback that is farther from that for the ancestral marine stickleback. Estimates are for the percentage of variation that a particular QTL explains for a particular geometric morphometric landmark or univariate measurement (the latter are shown on the fish image). Note that the lack of QTL of very small effect (<5% variance explained) reflects estimation limitations rather than the lack of such QTL. The stickleback image was provided by S Rogers.
Answer: Most QTL involved in adaptive divergence are of very small effect, but a few are of larger effect. This result does not by itself validate or reject the geometric model because the model assumptions are very different from empirical reality. First, the theory is based on new mutations, whereas standing variation is important in stickleback and most other organisms (see below). Second, the theory simultaneously considers all traits involved in adaptation, whereas empirical studies consider only a few traits. To narrow this gap, QTL studies should also map fitness, which integrates across all phenotypic traits.
Question 6: How parallel is genetic divergence?
Many studies report the independent (repeated) evolution of similar phenotypes in similar environments, either from similar or different ancestors. This ‘parallelism’ or ‘convergence’ of phenotypes implies, with caveats, a strong deterministic role for environmentally determined natural selection (Simpson, 1953; Mayr, 1963; Endler, 1986; Schluter, 2000; Arendt and Reznick, 2008; Losos, 2011). Another important questions is the extent to which parallelism/convergence is evident at the genetic level. At one extreme, adaptation by independent populations to similar environments could be driven by the same frequency changes in the same alleles (and nucleotides) at the same loci, with the relevant alleles at each locus having arisen only once (that is, identical by descent). Moving away from this extreme, the same allele might have had multiple origins, the alleles might be different but have similar effects, the alleles might be different and have different effects, and different genes might be involved in the different populations (Arendt and Reznick, 2008; Manceau et al., 2010; Linnen et al., 2013).
All of the above alternatives seem important in nature—even within the same study system. For instance, stickleback provide a nice example of a single allele involved in adaptation to a similar environment in multiple independent instances. Specifically, the low-plate EDA allele favored (and almost universally found) in fresh water arose once through mutation, is retained in marine stickleback because it is recessive, and increases toward fixation whenever marine stickleback colonize fresh water (Colosimo et al., 2005). At the same time, stickleback also provide a nice example of different alleles of the same gene (Pitx1) having the same phenotypic effect (pelvic reduction) in multiple independent instances (Chan et al., 2010). Divergence in Pitx1 is thus parallel at the level of the gene but not at the level of the allele. Additional examples of independent mutations at the same gene having similar phenotypic effects include FRI and flowering time in Arabidopsis (Shindo et al., 2005) and VNR1 and seasonal growth in cereal plants (Cockram et al., 2007). Importantly, parallelism even at the level of the gene is not universal even in the above cases: for instance, some freshwater stickleback populations show lateral plate reduction without variation in EDA (Leinonen et al., 2012; Lucek et al., 2012). Similarly diverse results are common in other organisms, with a well-described example being the evolution of color in animals (review: Manceau et al. 2010).
As the preceding examples illustrate, the genetics of adaptation run the gamut of possibilities from very high to very low parallelism (see also Flint and Mackay 2009), but can any generalities be drawn? Conte et al. (2012) reviewed genetic mapping and candidate gene studies for the extent to which the same genes were shared during adaptation by different lineages. By their calculations, mean probabilities of gene reuse were ‘0.32 for genetic mapping studies and 0.55 for candidate gene studies’ (Conte et al., 2012). They consider these estimates to be ‘surprisingly high’ and conclude that ‘Frequent reuse of the same genes during repeated phenotypic evolution suggests that strong biases and constraints affect adaptive evolution, resulting in changes at a relatively small subset of available genes’ (Conte et al., 2012). Without questioning the data itself (Figure 6), I find it easier to draw the opposite conclusion: gene reuse is low. For starters, a number of biases increase the estimated probabilities of gene reuse: publication bias against non-parallel patterns (particularly in candidate gene studies), the difficulty of detecting small effect genes in mapping studies (see above), the focus on traits as opposed to overall adaptation (see above), the explicit a priori focus on parallel phenotypic change (Conte et al., 2012), and the exclusion of unexplained phenotypic variance (which is often very high) from the calculations (Conte et al., 2012) (The authors discuss some of these biases, as well as others that might act in the opposite direction). Even ignoring any biases, the genetic mapping results find that the probability of non-reuse (68%) is more than twice the probability of reuse (32%). Evolution is thus considerably more likely to involve different genes in different instances than it is to involve the same genes.
Estimates of the proportional similarity of genes used in adaptation by different species pairs according to the age of their separation (Conte et al., 2012). A y-axis value of zero means that no genes are shared and a value of unity means that the sharing is perfect (for example, the same gene is responsible in the two taxa). Black triangles represent data from genetic crosses and gray circles represent data from candidate gene studies. A single point at 300 years (candidate gene study with 100% probability of gene reuse) is omitted to increase visibility in the rest of the data range.
Answer: The genetics of adaptation by independent populations to similar environments often will be non-parallel/non-convergent, certainly at the allele level and probably often also at the gene level. What we now need are inferential approaches that allow us to more objectively determine the portion of the genome that diverges between populations in different environments, and the proportion of that divergence that is or is not parallel/convergent at a given level.
Question 7: Standing genetic variation or new mutations?
Is adaptation to new conditions driven primarily by genetic variation already present in the population (standing) or is it primarily the result of new mutations (Barrett and Schluter, 2008)? At the most basic level, mutations are obviously important because standing variation started from new mutations—and these might have arisen and spread during previous adaptation. The question with a less obvious answer is: how much of the adaptation to a particular selective event is the result of mutations that arose during that event? Theoretical predictions are diverse (Hermisson and Pennings, 2005; Barrett and Schluter, 2008; Orr and Unckless, 2008; Rockman, 2012), but a common perception is that standing variation often will be most important, because the waiting time for adaptation is shorter, because adaptive alleles are less likely to be lost through drift, and because existing variation is more likely to have been tested by past selection. Exceptions occur when standing variation is limited (for example, due to inbreeding or strong past selection), mutational inputs are very high (for example, in large populations with short generation times or in the case of high mutation rates), and the new condition has not been previously experienced (for example, pesticides, herbicides, antibiotics and antivirals).
Empirically, the importance of standing variation is first implied by the earlier-described studies that report nearly ubiquitous additive genetic variance for fitness-related traits in natural populations (Question 1). Evolution would seem likely to start with this variation, as long as it is relevant to selection and not unduly constrained by correlations with other traits. Fitting this expectation, the immediate and dramatic evolutionary responses often seen in artificial selection experiments suggest that plenty of relevant variation is present (Moose et al., 2004; Hill and Kirkpatrick, 2010; Johansson et al., 2010; Lango Allen et al., 2010). Although the results of these studies might seem of questionable relevance because the selection was not ‘natural,’ similarly rapid responses have been observed in natural populations experiencing environmental change (Hendry and Kinnison, 1999; Reznick and Ghalambor, 2001; Hendry et al., 2008). These arguments, however, are indirect: they point to standing variation only because intuition suggests the changes were too fast to result from new mutations.
Additional evidence for the role of standing variation can be gained through three other approaches: signatures of selective sweeps in the genome, evidence that adaptive alleles in new populations were present in the ancestral population, and phylogenetic analyses that establish whether adaptive alleles arose before or after the environmental change (Barrett and Schluter, 2008). Application of these approaches to the aforementioned selection experiments on maize (Moose et al., 2004) and chickens (Johansson et al., 2010) strongly implicates standing genetic variation. Application to natural populations often yields a similar conclusion, with examples including lactose tolerance in humans (Myles et al., 2005), warfarin resistance in brown rats (Rattus norvegicus) (Pelz et al., 2005), malathion resistance in blowflies (Lucilia spp.) (Hartley et al., 2006), local adaptation in Arabidopsis thaliana (Fournier-Level et al., 2011), and several traits in stickleback (Colosimo et al., 2005; Miller et al., 2007; Kitano et al., 2008; Jones et al., 2012b). Of particular relevance, the evolutionary changes observed in many of these cases took place over relatively short time frames (decades to centuries).
Although many studies thus point to standing variation, evidence for the role of new mutations is also growing. Interestingly, this evidence often comes from some of the same systems and traits that were discussed above, including Pitx1 in stickleback, lactose tolerance in some human populations (Tishkoff et al., 2007), diazinon resistance in blowflies (Hartley et al., 2006), acetylcholinesterase resistance in Drosophila (Karasov et al., 2010) and local adaptation in Arabidopsis (Hancock et al., 2011). These studies suggest that new mutations can be important even when populations contain lots of standing variation, although not necessarily for the same traits. At present, not enough data exist to state more generally the relative importance of new mutations versus standing variation. However, one body of work that could prove especially relevant is that considering the population dynamics of predators and prey in laboratory chemostats (for example, Yoshida et al. 2003, Becks et al. 2010). The key design element of this work is that some chemostats start with only a single clone of prey, whereas others start with multiple clones. Evolution in the single-clone chemostats will require new mutations, whereas evolution in the multi-clone chemostats can proceed through standing variation. The observed dynamics are very different between these cases: the single-clone chemostats show a general lack of evolutionary change, whereas the multi-clone chemostats show dramatic and ongoing evolutionary change that has population dynamic consequences. Here, at least, standing genetic variation dramatically shapes eco-evolutionary dynamics, whereas new mutations seem unimportant.
Answer: Adaptation to new conditions likely involves a combination of standing genetic variation and new mutations. Although no thorough analysis yet exists, the relative importance of each would seem likely to depend on specific conditions. Standing variation should be especially important for outbred populations (where it will be higher) with moderate-to-long generation times (because fewer new mutations can arise) facing conditions that are not entirely novel (because standing variation will have been tested by past selection). By contrast, mutations should be increasingly important when populations are more inbred or are otherwise depleted in standing variation, when generation lengths are shorter, and when conditions are novel (for example, certain pollution or pesticides). Even under this last set of conditions, however, the contribution of standing variation could still be greater than that from new mutations.
Question 8: Are the genetic changes regulatory or structural?
An ongoing debate, here characterized in simple form, is whether evolution occurs mostly as a result of genetic changes that alter the amino-acid sequence of proteins (structural) versus genetic changes that alter the amount, timing or location of protein production (regulatory). Answering this question is important because the two types of changes can have very different evolutionary effects: for example, they represent different targets for mutation and they have different expectations for pleiotropic effects and selection (Hoekstra and Coyne, 2007; Wray, 2007; Carroll, 2008; Stern and Orgogozo, 2008). Although regulatory changes can occur in several ways, much of the current debate has focused on cis-regulatory regions: short, noncoding sequences that influence the expression of a nearby gene.
Stern and Orgogozo (2008) compiled a database of individual genetic mutations influencing phenotypic traits in ‘domesticated species (99 cases), intraspecific variation in wild species (157 cases), and interspecific differences (75 cases).’ Of these mutations, 22% involved cis-regulatory regions and the authors argue that this is a major underestimate owing to investigator bias. Their survey additionally suggested that cis-regulatory mutations are more important for morphological traits (as opposed to physiological traits) and in interspecific comparisons (as opposed to domesticated species and intraspecific comparisons) (Figure 7). The first observation was interpreted as support for the importance of pleiotropy. Specifically, genes embedded more deeply in regulatory networks (hypothesized to be the case for morphology as opposed to physiology) are more likely to evolve through cis-regulatory changes because they are less likely to disrupt the entire network. The second observation was suggested to imply that the more subtle and local changes that can result from cis-regulatory mutations are more likely to be fixed during evolution over longer time periods.
The proportion of mutations contributing to phenotypic changes that are cis-regulatory mutations. These data were compiled by Stern and Orgogozo (2008) from studies that provided ‘compelling’ evidence for individual genetic mutations influencing variation in either morphological traits or physiological traits in domesticated species, intraspecific comparisons, interspecific comparisons and comparisons above the species level (>interspecific). The numbers above each bar give the total number of mutations per category.
Objectively obtained, whole-genome data on structural versus regulatory variation are rare, but a recent study of stickleback provides an exemplar. Jones et al. (2012b) performed full-genome sequencing of 21 individual stickleback representing freshwater and marine forms across the northern hemisphere. Of the 64 genomic regions showing the strongest evidence of parallel habitat-associated divergence (that is, the same freshwater versus marine genetic changes at different places in the world), 17% were in coding regions, 41% were in noncoding regions and 42% included both coding and noncoding sequences. All of the latter regions involved alleles that did not cause protein-coding changes. The authors interpreted these results to imply that at least 41%, and perhaps as much as 83%, of the most important and parallel genomic regions influencing adaptation involved regulatory mutations.
Answer: Both structural and regulatory genetic changes contribute to adaptation, but the rarity of objective studies and the existence of biases mean that their relative contributions are not yet clear. However, this question might not be the most interesting one anyway. Perhaps we should instead be asking ‘what kinds of phenotypic changes (for example, morphological versus physiological) are expected under particular coding versus cis-regulatory changes’ (Stern and Orgogozo, 2008) or ‘whether cis-regulatory mutations have a qualitatively distinct role (as opposed to other types of mutations) in phenotypic evolution’ (Wray, 2007). Returning to my earlier assertions, it will be important to consider these questions in the context of overall adaptation (fitness) and to find more sensitive and objective ways to detect non-parallel effects.
Question 9: How heritable are ecological effects?
A premise of this paper has been that the genetics and genomics of eco-evolutionary dynamics are largely equivalent to the genetics and genomics of phenotypes, at least to the extent that studying the latter provides a good foundation for understanding the former. For instance, a change in some ecological variable at the population, community or ecosystem level might be predicted from information about selection acting on traits, genetic (co)variances for traits, and the ecological effects of traits (Collins and Gardner, 2009; Johnson et al., 2009; Ellner et al., 2011). A limitation of this approach is that the traits having large effects on ecological variables are often unknown. An alternative approach is to consider the ecological effects of individuals as ‘extended phenotypes’ (or ‘interspecific indirect genetic effects’) and directly estimating their heritability or evolvability (Fritz and Price, 1988; Johnson and Agrawal, 2005; Shuster et al., 2006). That is, standard quantitative genetic methods can be used to relate the ecological effects of individuals to the genetic relationships among them (parent–offspring, half-sibs, and so on) and thereby estimate the heritability of the ecological effects of organisms, which I will here call ‘ecological heritabilities.’
A number of studies have estimated ecological heritabilities—usually for community-level variables and usually based on broad-sense estimates (proportion of the total variance due to all genetic effects). For example, Shuster et al. (2006) studied cottonwood (Populus spp.) trees planted in a common garden experiment in nature with multiple replicate clones of each of multiple tree genotypes. Arthropod communities were assessed on each individual tree and the proportion of the total variance in arthropods attributed to tree genotypes was estimated. The resulting broad-sense heritabilities were 56–68% for arthropod community composition, 30–34% for arthropod species richness and 31–43% for arthropod abundance (Shuster et al., 2006; Keith et al., 2010). In addition, Keith et al. (2010) showed that these estimates were remarkably constant across the same trees in 3 different years, such that the broad-sense heritability of community similarity was 32%. This last estimate indicates that arthropod communities were more consistent between years on some genotypes than on others: the highest similarity for a genotype was 61% and the lowest was 24%. Studies of other plant systems have estimated heritabilities of arthropod community variables at 9–51% (Fritz and Price, 1988) and 0–43% (Johnson and Agrawal, 2005). Future work would ideally estimate ecological heritabilities in the narrow sense (proportion of the total variance due to additive genetic effects) and for more types of ecological variables.
In principle, one could theoretically estimate ‘selection’ on an ecological variable as though it were an organismal phenotype and multiply this selection by the ecological heritability to predict at least short-term changes in the ecological variable. Although this thinking stretches the traditional meaning of ‘selection’, it could provide a trait-independent, whole-organism approach to predicting how selection on organisms might drive evolutionary changes that alter ecological variables. Even more directly (but with more difficulty), predictions of this sort can be obtained by measuring genetic covariances between the fitness of individuals and their ecological effects (Johnson et al., 2009). Of course, the accuracy of such predictions in nature will depend on the extent to which other factors also influence the ecological variables. That is, ecological effects owing to the evolution of one species might be washed out by other factors influencing the same variable.
Answer: The ecological ‘extended phenotypes’ of organisms are heritable in at least some instances, perhaps just as heritable as the traits themselves. Given that traits can evolve on contemporary time scales (Hendry and Kinnison, 1999; Reznick and Ghalambor, 2001), the same would seem likely for ecological variables. However, the degree to which different ecological variables are heritable is highly variable (Fritz and Price, 1988), and so we can’t assume that ecological variables will always be so responsive to selection on organisms.
A way forward
Some conceptualizations of eco-evolutionary dynamics are couched in terms of ‘genes to ecosystems’ (Elser et al., 2000; Whitham et al., 2006; Bailey, et al., 2009b; Schweitzer, et al., 2009). Some readers might interpret this phrasing to mean that we should be searching for particular genes that have large ecological effects and, indeed, a few such genes have been found. For example, PGI influences population dynamics in Glanville fritillary (Melitaea cinxia) butterflies (Hanski and Saccheri, 2006). Overall, however, I suggest that searching for particular genes of large ecological effect, while perhaps flashy and more likely to be rewarded by publication in fancy journals, is not the best approach to the genetics and genomics of eco-evolutionary dynamics. A key reason is that phenotypes are the interface between ecology and evolution, with genes only being indirectly relevant through their effects on phenotypes. Eco-evolutionary investigations therefore should be concerned with the genetics and genomics of phenotypic adaptation, which I have here argued is based mostly on standing genetic variation at many genes of small-to-modest effect. Thus, while the search for particular genes that have ecological effects will sometimes be successful, it will miss the majority of the important links between evolution and ecology. Instead, we should implement approaches that can examine and quantify the polygenic basis of eco-evolutionary dynamics. Such work will undoubtedly involve a mixture of quantitative genetics (including non-additive effects), genome scans (with improved inferential methods) and gene expression (because many phenotypic differences between populations appear to be regulatory). If effort and encouragement is focused in these directions, I expect the greatest and most general advances in the genetics and genomics of eco-evolutionary dynamics to result.
Data archiving
There were no data to deposit.
References
Agrawal AF, Stinchcombe JR . (2009). How much do genetic covariances alter the rate of adaptation? ProcR Soc B Biol Sci 276: 1183–1191.
Albert AYK, Sawaya S, Vines TH, Knecht AK, Miller CT, Summers BR et al. (2008). The genetics of adaptive shape shift in stickleback: pleiotropy and effect size. Evolution 62: 76–85.
Arendt J, Reznick D . (2008). Convergence and parallelism reconsidered: what have we learned about the genetics of adaptation? Trends Ecol Evol 23: 26–32.
Bailey JK, Hendry AP, Kinnison MT, Post DM, Palkovacs EP, Pelletier F et al. (2009a). From genes to ecosystems: an emerging synthesis of eco-evolutionary dynamics. N Phytol 184: 746–749.
Bailey JK, Schweitzer JA, Úbeda F, Koricheva J, LeRoy CJ, Madritch MD et al. (2009b). From genes to ecosystems: a synthesis of the effects of plant genetic factors across levels of organization. Phil Trans R Soc B Biol Sci 364: 1607–1616.
Barrett RDH, Hendry AP . (2012). Evolutionary rescue under environmental change? In: Candolin U, Wong BBM (eds) Behavioural responses to a changing world: mechanisms and consequences. Oxford University Press: London, UK. pp 216–233.
Barrett RDH, Rogers SM, Schluter D . (2008). Natural selection on a major armor gene in threespine stickleback. Science 322: 255–257.
Barrett RDH, Schluter D . (2008). Adaptation from standing genetic variation. Trends Ecol Evol 23: 38–44.
Bassar RD, Ferriere R, López-Sepulcre A, Marshall MC, Travis J, Pringle CM et al. (2012). Direct and indirect ecosystem effects of evolutionary adaptation in the Trinidadian guppy (Poecilia reticulata). Am Nat 180: 167–185.
Becks L, Ellner SP, Jones LE, Hairston NG . (2010). Reduction of adaptive genetic diversity radically alters eco-evolutionary community dynamics. Ecol Lett 13: 989–997.
Bell G, Gonzalez A . (2011). Adaptation and evolutionary rescue in metapopulations experiencing environmental deterioration. Science 332: 1327–1330.
Bernatchez L, Renaut S, Whiteley AR, Derome N, Jeukens J, Landry L et al. (2010). On the origin of species: insights from the ecological genomics of lake whitefish. Phil Trans R Soc B Biol Sci 365: 1783–1800.
Berner D, Kaeuffer R, Grandchamp A-C, Raeymaekers JAM, Räsänen K, Hendry AP . (2011). Quantitative genetic inheritance of morphological divergence in a lake-stream stickleback ecotype pair: implications for reproductive isolation. J Evol Biol 24: 1975–1983.
Blows MW, Chenoweth SF, Hine E . (2004). Orientation of the genetic variance-covariance matrix and the fitness surface for multiple male sexually selected traits. Am Nat 163: 329–340.
Blows MW, Hoffmann AA . (2005). A reassessment of genetic limits to evolutionary change. Ecology 86: 1371–1384.
Bradshaw AD, McNeilly T . (1991). Evolutionary response to global climate change. Ann Botany 67: 5–14.
Buerkle CA, Lexer C . (2008). Admixture as the basis for genetic mapping. Trends Ecol Evol 23: 686–694.
Bürger R . (1986). Constraints for the evolution of functionally coupled characters: a nonlinear analysis of a phenotypic model. Evolution 40: 182–193.
Carroll SP . (2007). Brave New World: the epistatic foundations of natives adapting to invaders. Genetica 129: 193–204.
Carroll SB . (2008). Evo-devo and an expanding evolutionary synthesis: A genetic theory of morphological evolution. Cell 134: 25–36.
Carroll SP, Dingle H, Famula TR . (2003). Rapid appearance of epistasis during adaptive divergence following colonization. ProcR Soc B Biol Sci 270: S80–S83.
Carroll SP, Dingle H, Famula TR, Fox CW . (2001). Genetic architecture of adaptive differentiation in evolving host races of the soapberry bug, Jadera haematoloma. Genetica 112–113: 257–272.
Chan YF, Marks ME, Jones FC, Villarreal G Jr, Shapiro MD, Brady SD et al. (2010). Adaptive evolution of pelvic reduction of a Pitx1 enhancer. Science 327: 302–305.
Cockram J, Mackay IJ, Sullivan DMO . (2007). The role of double-stranded break repair in the creation of phenotypic diversity at cereal VRN1 loci. Genetics 177: 2535–2539.
Collins S, Gardner A . (2009). Integrating physiological, ecological and evolutionary change: a Price equation approach. Ecol Lett 12: 744–757.
Colosimo PF, Hosemann KE, Balabhadra S, Villarreal G Jr, Dickson M, Grimwood J et al. (2005). Widespread parallel evolution in sticklebacks by repeated fixation of Ectodysplasin alleles. Science 307: 1928–1933.
Conte GL, Arnegard ME, Peichel CL, Schluter D . (2012). The probability of genetic parallelism and convergence in natural populations. Proc R Soc B Biol Sci 279: 5039–5047.
Ellner SP, Hairston NG Jr, Geber MA . (2011). Does rapid evolution matter? Measuring the rate of contemporary evolution and its impacts on ecological dynamics. Ecol Lett 14: 603–614.
Elser JJ, Sterner RW, Gorokhova E, Fagan WF, Markow TA, Cotner JB et al. (2000). Biological stoichiometry from genes to ecosystems. Ecol Lett 3: 540–550.
Endler JA . (1986) Natural selection in the wild. Princeton University Press: Princeton.
Falconer DS, Mackay TFC . (1996) Introduction to quantitative genetics 4th edn. Longman Science and Technology: Harlow, UK.
Fisher RA . (1930) The genetical theory of natural selection. Oxford University Press: Oxford.
Flint J, Mackay TFC . (2009). Genetic architecture of quantitative traits in mice, flies, and humans. Genome Res 19: 723–733.
Fournier-Level A, Korte A, Cooper MD, Nordborg M, Schmitt J, Wilczek AM . (2011). A map of local adaptation in Arabidopsis thaliana. Science 334: 86–89.
Fritz RS, Price PW . (1988). Genetic variation among plants and insect community structure: willows and sawflies. Ecology 69: 845–856.
Fussmann GF, Loreau M, Abrams PA . (2007). Eco-evolutionary dynamics of communities and ecosystems. Functional Ecol 21: 465–477.
Futuyma DJ, Keese MC, Funk DJ . (1995). Genetic constraints on macroevolution - the evolution of host affiliation in the leaf beetle Genus Ophraella. Evolution 49: 797–809.
Gilad Y, Pritchard JK, Thornton K . (2009). Characterizing natural variation using next-generation sequencing technologies. Trends Genet 25: 463–471.
Hairston NG, Ellner SP, Geber MA, Yoshida T, Fox JA . (2005). Rapid evolution and the convergence of ecological and evolutionary time. Ecol Lett 8: 1114–1127.
Hancock AM, Brachi B, Faure N, Horton MW, Jarymowycz LB, Sperone FG et al. (2011). Adaptation to climate across the Arabidopsis thaliana genome. Science 334: 83–86.
Hansen TF, Houle D . (2008). Measuring and comparing evolvability and constraint in multivariate characters. J Evol Biol 21: 1201–1219.
Hansen TF, Pélabon C, Houle D . (2011). Heritability is not evolvability. Evol Biol 38: 258–277.
Hanski I, Mononen T, Ovaskainen O . (2011). Eco-evolutionary metapopulation dynamics and the spatial scale of adaptation. Am Nat 177: 29–43.
Hanski I, Saccheri I . (2006). Molecular-level variation affects population growth in a butterfly metapopulation. PLoS Biol 4: e129.
Harmon LJ, Matthews B, Des Roches S, Chase JM, Shurin JB, Schluter D . (2009). Evolutionary diversification in stickleback affects ecosystem functioning. Nature 458: 1167–1170.
Hartley CJ, Newcomb RD, Russell RJ, Yong CG, Stevens JR, Yeates DK et al. (2006). Amplification of DNA from preserved specimens shows blowflies were preadapted for the rapid evolution of insecticide resistance. Proc Natl Acad Sci USA 103: 8757–8762.
Hellmann J, Pinedakrch M . (2007). Constraints and reinforcement on adaptation under climate change: Selection of genetically correlated traits. Biol Conserv 137: 599–609.
Hendry AP, Farrugia TJ, Kinnison MT . (2008). Human influences on rates of phenotypic change in wild animal populations. Mol Ecol 17: 20–29.
Hendry AP, Kinnison MT . (1999). The pace of modern life: measuring rates of contemporary microevolution. Evolution 53: 1637–1653.
Hereford J, Hansen TF, Houle D . (2004). Comparing strengths of directional selection: how strong is strong? Evolution 58: 2133–2143.
Hermisson J, Pennings PS . (2005). Soft sweeps: molecular population genetics of adaptation from standing genetic variation. Genetics 169: 2335–2352.
Hill WG . (2010). Understanding and using quantitative genetic variation. Philos Trans R Soc B Biol Sci 365: 73–85.
Hill WG, Goddard ME, Visscher PM . (2008). Data and theory point to mainly additive genetic variance for complex traits. PLoS Genet 4: e1000008.
Hill WG, Kirkpatrick M . (2010). What animal breeding has taught us about evolution. Annu Rev Ecol Evol Syst 41: 1–19.
Hoekstra HE, Coyne JA . (2007). The locus of evolution: evo devo and the genetics of adaptation. Evolution 61: 995–1016.
Hoffmann AA, Hallas RJ, Dean JA, Schiffer M . (2003). Low potential for climatic stress adaptation in a rainforest Drosophila species. Science 301: 100–102.
Hohenlohe PA, Bassham S, Etter PD, Stiffler N, Johnson EA, Cresko WA . (2010). Population genomics of parallel adaptation in threespine stickleback using sequenced RAD tags. PLoS Genet 6: e1000862.
Houle D . (1992). Comparing evolvability and variability of quantitative traits. Genetics 130: 195–204.
Hughes AR, Inouye BD, Johnson MTJ, Underwood N, Vellend M . (2008). Ecological consequences of genetic diversity. Ecol Lett 11: 609–623.
Johansson AM, Pettersson ME, Siegel PB, Carlborg Ö . (2010). Genome-wide effects of long-term divergent selection. PLoS Genet 6: e1001188.
Johnson MTJ, Agrawal AA . (2005). Plant genotype and environment interact to shape a diverse arthropod community on evening primrose (Oenothera biennis). Ecology 86: 874–885.
Johnson MTJ, Vellend M, Stinchcombe JR . (2009). Evolution in plant populations as a driver of ecological changes in arthropod communities. Philos Trans R Soc B Biol Sci 364: 1593–1605.
Jones FC, Chan YF, Schmutz J, Grimwood J, Brady SD, Southwick AM et al. (2012a). A genome-wide SNP genotyping array reveals patterns of global and repeated species-pair divergence in sticklebacks. Curr Biol 22: 83–90.
Jones FC, Grabherr MG, Chan YF, Russell P, Mauceli E, Johnson J et al. (2012b). The genomic basis of adaptive evolution in threespine sticklebacks. Nature 484: 55–61.
Karasov T, Messer PW, Petrov DA . (2010). Evidence that adaptation in Drosophila is not limited by mutation at single sites. PLoS Genet 6: e1000924.
Keith AR, Bailey JK, Whitham TG . (2010). A genetic basis to community repeatability and stability. Ecology 91: 3398–3406.
Kellermann VM, Van Heerwaarden B, Hoffmann AA, Sgrò CM . (2006). Very low additive genetic variance and evolutionary potential in multiple populations of two rainforest Drosophila species. Evolution 60: 1104–1108.
Kellermann V, Van Heerwaarden B, Sgrò CM, Hoffmann AA . (2009). Fundamental evolutionary limits in ecological traits drive Drosophila species distributions. Science 325: 1244–1246.
Kinnison MT, Hairston NG Jr . (2007). Eco-evolutionary conservation biology: contemporary evolution and the dynamics of persistence. Functional Ecol 21: 444–454.
Kirkpatrick M . (2009). Patterns of quantitative genetic variation in multiple dimensions. Genetica 136: 271–284.
Kitano J, Bolnick DI, Beauchamp DA, Mazur MM, Mori S, Nakano T et al. (2008). Reverse evolution of armor plates in the threespine stickleback. Curr Biol 18: 769–774.
Kitano J, Lema SC, Luckenbach JA, Mori S, Kawagishi Y, Kusakabe M et al. (2010). Adaptive divergence in the thyroid hormone signaling pathway in the stickleback radiation. Curr Biol 20: 1–7.
Kruglyak L . (2008). The road to genome-wide association studies. Nature 9: 314–318.
Lango Allen H, Estrada K, Lettre G, Berndt SI, Weedon MN, Rivadeneira F et al. (2010). Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature 467: 832–838.
Leinonen T, McCairns RJS, Herczeg G, Merilä J . (2012). Multiple evolutionary pathways to decreased lateral plate coverage in freshwater threespine sticklebacks. Evolution 66: 3866–3875.
Linnen CR, Poh Y-P, Peterson BK, Barrett RDH, Larson JG, Jensen JD et al. (2013). Adaptive evolution of multiple traits through multiple mutations at a single gene. Science 339: 1312–1316.
Losos JB . (2011). Convergence, adaptation, and constraint. Evolution 65: 1827–1840.
Lucek K, Haesler MP, Sivasundar A . (2012). When phenotypes do not match genotypes—unexpected phenotypic diversity and potential environmental constraints in Icelandic stickleback. J Heredity 103: 579–584.
Lynch M, Walsh B . (1998) Genetics and analysis of quantitative traits. Sinauer Associates, Inc.: Sunderland, MA, USA.
Mackay TFC, Stone EA, Ayroles JF . (2009). The genetics of quantitative traits: challenges and prospects. Nat Rev Genet 10: 565–577.
Manceau M, Domingues VS, Linnen CR, Rosenblum EB, Hoekstra HE . (2010). Convergence in pigmentation at multiple levels: mutations, genes and function. Philos Trans R Soc London Series B Biol Sci 365: 2439–2450.
Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ et al. (2009). Finding the missing heritability of complex diseases. Nature 461: 747–753.
Matsubayashi KW, Ohshima I, Nosil P . (2010). Ecological speciation in phytophagous insects. Entomolo Exp Appl 134: 1–27.
Matsumura S, Arlinghaus R, Dieckmann U . (2012). Standardizing selection strengths to study selection in the wild: a critical comparison and suggestions for the future. BioScience 62: 1039–1054.
Matthews B, Narwani A, Hausch S, Nonaka E, Peter H, Yamamichi M et al. (2011). Toward an integration of evolutionary biology and ecosystem science. Ecol Lett 14: 690–701.
Mayr E . (1963) Animal species and evolution. Belknap Press: Cambridge.
McGuigan K, Blows MW . (2007). The phenotypic and genetic covariance structure of drosphilid wings. Evolution 61: 902–911.
Mezey JG, Houle D . (2005). The dimentsionality of genetic variation for wing shape in Drosophila melanogaster. Evolution 59: 1027–1038.
Michel AP, Sim S, Powell THQ, Taylor MS, Nosil P, Feder JL . (2010). Widespread genomic divergence during sympatric speciation. Proc Natl Acad Sci USA 107: 9724–9729.
Miller CT, Beleza S, Pollen AA, Schluter D, Kittles RA, Shriver MD et al. (2007). cis-regulatory changes in Kit ligand expression and parallel evolution of pigmentation in sticklebacks and humans. Cell 131: 1179–1189.
Moose SP, Dudley JW, Rocheford TR . (2004). Maize selection passes the century mark: a unique resource for 21st century genomics. Trends Plant Sci 9: 358–364.
Morjan CL, Rieseberg LH . (2004). How species evolve collectively: implications of gene flow and selection for the spread of advantageous alleles. Mol Ecol 13: 1341–1356.
Mousseau TA, Roff DA . (1987). Natural selection and the heritability of fitness components. Heredity 59: 181–197.
Myles S, Bouzekri N, Haverfield E, Cherkaoui M, Dugoujon J-M, Ward R . (2005). Genetic evidence in support of a shared Eurasian-North African dairying origin. Hum Genet 117: 34–42.
Nosil P, Funk DJ, Ortiz-Barrientos D . (2009). Divergent selection and heterogeneous genomic divergence. Mol Ecol 18: 375–402.
Olson-Manning CF, Wagner MR, Mitchell-Olds T . (2012). Adaptive evolution: evaluating empirical support for theoretical predictions. Nat Rev Genet 13: 867–877.
Orr HA . (1999). The evolutionary genetics of adaptation: a simulation study. Genet Res 74: 207–214.
Orr HA . (2005). The genetic theory of adaptation: a brief history. Nat Rev Genet 6: 119–127.
Orr HA, Unckless RL . (2008). Population extinction and the genetics of adaptation. Am Nat 172: 160–169.
Otto SP, Jones CD . (2000). Detecting the undetected: estimating the total number of loci underlying a quantitative trait. Genetics 156: 2093–2107.
Palkovacs EP, Post DM . (2009). Experimental evidence that phenotypic divergence in predators drives community divergence in prey. Ecology 90: 300–305.
Pavey SA, Collin H, Nosil P, Rogers SM . (2010). The role of gene expression in ecological speciation. Ann NY Acad Sci 1206: 110–129.
Peichel CL, Nereng KS, Ohgi KA, Cole BLE, Colosimo PF, Buerkle CA et al. (2001). The genetic architecture of divergence between threespine stickleback species. Nature 414: 901–905.
Pelletier F, Garant D, Hendry AP . (2009). Eco-evolutionary dynamics. Philos Trans R Soc B Biol Sci 364: 1483–1489.
Pelz H-J, Rost S, Hünerberg M, Fregin A, Heiberg A-C, Baert K et al. (2005). The genetic basis of resistance to anticoagulants in rodents. Genetics 170: 1839–1847.
Phillips PC . (2008). Epistasis - the essential role of gene interactions in the structure and evolution of genetic systems. Nat Rev Genet 9: 855–867.
Post DM, Palkovacs EP . (2009). Eco-evolutionary feedbacks in community and ecosystem ecology: interactions between the ecological theatre and the evolutionary play. Philos Trans R Soc B Biol Sci 364: 1629–1640.
Provine WB . (1971) The origins of theoretical population genetics. University of Chicago Press: Chicago.
Renaut S, Nolte AW, Bernatchez L . (2009). Gene expression divergence and hybrid misexpression between lake whitefish species pairs (Coregonus spp. Salmonidae). Mol Biol Evol 26: 925–936.
Renaut S, Nolte AW, Rogers SM, Derome N, Bernatchez L . (2011). SNP signatures of selection on standing genetic variation and their association with adaptive phenotypes along gradients of ecological speciation in lake whitefish species pairs (Coregonus spp.). Mol Ecol 20: 545–559.
Reznick DN, Ghalambor CK . (2001). The population ecology of contemporary adaptations: what empirical studies reveal about the conditions that promote adaptive evolution. Genetica 112-113: 183–198.
Rockman MV . (2012). The QTN program and the alleles that matter for evolution: all that’s gold does not glitter. Evolution 66: 1–17.
Roesti M, Hendry AP, Salzburger W, Berner D . (2012). Genome divergence during evolutionary diversification as revealed in replicate lake–stream stickleback population pairs. Mol Ecol 21: 2852–2862.
Roff DA . (1996). The evolution of genetic correlations: an analysis of patterns. Evolution 50: 1392–1403.
Roff DA . (1997) Evolutionary Quantitative Genetics. Chapman and Hall: New York.
Roff DA, Emerson K . (2006). Epistasis and dominance: evidence for differential effects in life-history versus morphological traits. Evolution 60: 1981–1990.
Rogers SM, Tamkee P, Summers B, Balabahadra S, Marks M, Kingsley DM et al. (2012). Genetic signature of adaptive peak shift in threespine stickleback. Evolution 66: 2439–2450.
Saccheri I, Hanski I . (2006). Natural selection and population dynamics. Trends Ecol Evol 21: 341–347.
Schluter D . (2000) The Ecology of Adaptive Radiation. Oxford University Press.
Schoener TW . (2011). The newest synthesis: understanding the interplay of evolutionary and ecological dynamics. Science 331: 426–429.
Shimada Y, Shikano T, Merilä J . (2010). A high incidence of selection on physiologically important genes in the three-spined stickleback, Gasterosteus aculeatus. Mol Biol Evol 28: 181–193.
Shindo C, Aranzana MJ, Lister C, Baxter C, Nicholls C, Nordborg M et al. (2005). Role of FRIGIDA and FLOWERING LOCUS C in determining variation in flowering time of Arabidopsis. Plant Physiol 138: 1163–1173.
Shuster SM, Lonsdorf EV, Wimp GM, Bailey JK, Whitham TG . (2006). Community heritability measures the evolutionary consequences of indirect genetic effects on community structure. Evolution 60: 991–1003.
Simpson GG . (1953) The major features of evolution. Columbia University Press: New York.
Stapley J, Reger J, Feulner PGD, Smadja C, Galindo J, Ekblom R et al. (2010). Adaptation Genomics: the next generation. Trends Ecol Evol 25: 705–712.
Stern DL, Orgogozo V . (2008). The loci of evolution: how predictable is genetic evolution? Evolution 62: 2155–2177.
Stinchcombe JR, Hoekstra HE . (2008). Combining population genomics and quantitative genetics: finding the genes underlying ecologically important traits. Heredity 100: 158–170.
Thompson JN . (1998). Rapid evolution as an ecological process. Trends Ecol Evol 13: 329–332.
Tishkoff SA, Reed FA, Ranciaro A, Voight BF, Babbitt CC, Silverman JS et al. (2007). Convergent adaptation of human lactase persistence in Africa and Europe. Nat Genet 39: 31–40.
Wade MJ . (2002). A gene’s eye view of epistasis, selection and speciation. J Evol Biol 15: 337–346.
Walsh B, Blows MW . (2009). Abundant genetic variation+strong selection=multivariate genetic constraints: a geometric view of adaptation. Annu Rev Ecol Evol Syst 40: 41–59.
West Eberhard MJ . (2003) Developmental plasticity and evolution. Oxford University Press: Oxford.
Whitham TG, Bailey JK, Schweitzer JA, Shuster SM, Bangert RK, LeRoy CJ et al. (2006). A framework for community and ecosystem genetics: from genes to ecosystems. Nat Rev Genet 7: 510–523.
Wolf JB, Brodie ED III, Wade MJ . (2000) Epistasis and the evolutionary process. Oxford University Press: Oxford.
Wray GA . (2007). The evolutionary significance of cis-regulatory mutations. Nat Rev Genet 8: 206–216.
Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR et al. (2010). Common SNPs explain a large proportion of the heritability for human height. Nat Genet 42: 565–569.
Yoshida T, Jones LE, Ellner SP, Fussmann GF, Hairston NG Jr. . (2003). Rapid evolution drives ecological dynamics in a predator-prey system. Nature 424: 303–306.
Acknowledgements
I thank the following people for comments on specific aspects of the paper or for invigorating arguments on the topics in general: Katie Peichel, Dan Bolnick, Dan Berner, Dolph Schluter, Gina Conte, Sean Rogers, Patrik Nosil, Rowan Barrett, Graham Bell, Rees Kassen, Sean Rogers, Marc Johnson, Jen Schweitzer, Louis Bernatchez, Derek Roff, and Hans Larsson. I would like to especially thank Katie Peichel for twice providing comments on the entire manuscript. The paper was further improved by comments from Oscar Gaggiotti and two anonymous reviewers. For providing data in the figures, I thank Thomas Hansen, Aneil Agrawal, Sean Rogers, David Stern and Gina Conte.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The author declares no conflict of interest.
Rights and permissions
About this article
Cite this article
Hendry, A. Key questions in the genetics and genomics of eco-evolutionary dynamics. Heredity 111, 456–466 (2013). https://doi.org/10.1038/hdy.2013.75
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/hdy.2013.75
Keywords
This article is cited by
-
Genomic signatures of natural selection at phenology-related genes in a widely distributed tree species Fagus sylvatica L
BMC Genomics (2021)
-
The long-term restoration of ecosystem complexity
Nature Ecology & Evolution (2020)
-
Contemporary ancestor? Adaptive divergence from standing genetic variation in Pacific marine threespine stickleback
BMC Evolutionary Biology (2018)
-
Species-rich networks and eco-evolutionary synthesis at the metacommunity level
Nature Ecology & Evolution (2017)
-
What genomic data can reveal about eco-evolutionary dynamics
Nature Ecology & Evolution (2017)