Introduction

Simple methods for calculating the statistical power for detecting a QTL that overlaps with a marker have been developed (Soller et al., 1976; Muranty, 1996). When the QTL of interest is located further away from a marker, which is used to detect the QTL, the power will be decreased (Soller and Genizi, 1978; Lynch and Walsh, 1998). Simple methods for calculating the statistical power for a QTL located in an interval flanked by two markers have not been available. Statistical methods for power calculation based on the likelihood ratio test statistic using markers of the entire genome (interval mapping) have been developed by Dupuis and Siegmund (1999). However, the methods depend on some assumptions such as infinitely high marker density or equal distance of marker distribution, and thus they can be very complicated. Simple regression method for QTL mapping (Haley and Knott, 1992) is a good approximation of the maximum likelihood method. Therefore, statistical power may be calculated based on the simple regression method. Because of the simplicity of the regression method, calculation of statistical power under this method is also simple. If the QTL of interest does not overlap with a marker, the power of detecting this QTL will be decreased. The worst-case scenario is that the QTL sits in the middle of the largest marker interval. If we can compute the statistical power for detecting such a QTL, the inverse power function will allow us to design a QTL mapping experiment regarding the sample size and the minimum marker density required. This article will introduce such a simple method.

Methods

We now use an F2 mating design as an example to develop the method. Extension to other mating types will be described later in the Discussion section. Although t-test is commonly used for the simple regression analysis, F-test is used here to discuss the power calculation because we can avoid the confusion between one-tailed and two-tailed tests that occur in the t-test. With the F-test, only a single tail of the distribution is concerned. In addition, when only additive effect is considered, the F-test statistic is simply the square of the t-test statistic. Let A1A1, A1A2 and A2A2 be the three genotypes of a QTL in an F2 family. Let

be the genotype indicator variable for individual j for j=1, … n, where n is the sample size. Let a be the additive genetic effect (the difference between the genotypic values of A1A1 and A1A2). Assume that the QTL of interest overlaps with a fully informative marker, the test statistic under the regression analysis is

where â is the least square estimate of the genetic effect and ς̂2 is the estimated residual error variance. Under the null hypothesis (a=0), the above test statistic will follow a central F-distribution with degrees of freedom 1 and n (assuming that n is sufficiently large). Under the alternative hypothesis (a≠0), the test statistic will follow a non-central F-distribution with degrees of freedom 1 and n and a non-centrality parameter

where σx2=1/2 is the variance of variable x across all individuals within the F2 family (assuming that there is no segregation distortion). Let F(λ∣1, n, 0) and F(λ∣1, n, δ) be the central and non-central F-distribution functions for variable λ, respectively. Define λ1−α as the 1−α percentile of the central F-distribution, that is, α=Pr(λ>λ1−α∣δ=0)=1−F(λ1−α∣1, n, 0) or

where α is the Type I error. The Type II error is defined as β=Pr(λ⩽λ1−α∣δ>0), that is,

The statistical power is

To calculate the statistical power for a given Type I error α, we first use equation (4) to find the critical value λ1−α and then use equation (5) to calculate the Type II error β, and finally use equation (6) to get the statistical power γ.

The three steps used to calculate the statistical power is general for all experiments using the F-test statistic. The non-centrality parameter δ, however, depends on the experimental parameters of the specific experiment. In addition, if the QTL of interest does not overlap with a marker, the non-centrality parameter should be revised to take into account the linkage information between the QTL and markers.

Let m1 and m2 be the genotype indicator variables (similarly defined as variable x) for two flanking markers. Let r1 and r2 be the recombination fractions between m1 and x and between x and m2, respectively. The recombination fraction between m1 and m2 is r12=r1+r2−2r1r2. Let x̂=E(x∣m1,m2) be the conditional expectation of x given m1 and m2. The non-centrality parameter for F-test using ◯ as the independent variable is

where σx2=1/2 in the F2 population and

is the variance of ◯ across individuals within the mapping population. The denominator of the non-centrality parameter is increased by a2(σx2−σ◯2), which is the inflation parameter for the residual variance due to uncertainty of the QTL genotype (Xu, 1995).

Assume that the QTL of interest sits in the middle of the interval between markers m1 and m2 so that r1=r2=r and r12=2r(1−r). The above variance for x̂ is simplified to

One can verify that when the QTL overlaps with both markers (the marker interval is infinitely small), that is, r=0, we get σ◯2=1/2, leading to the same non-centrality parameter given in equation (3). However, if the QTL sits in the middle of an infinitely large marker interval, that is, r=0.5, we have σ◯2=0, leading to a zero non-centrality parameter and thus zero power.

Given the statistical power and the Type I error, one can find the non-centrality parameter using the following inverse function,

where F−1 is the inverse F-distribution function with the inverse referring to the non-centrality parameter, not the quantile. We use a subscript −1 to distinguish the non-centrality inverse F-distribution function from the traditional quantile inverse F-distribution function (with a superscript −1). Once the non-centrality parameter is calculated, we can find the sample size required given the size of a marker interval or the marker interval required given a fixed sample size.

Examples

We now show a few examples for calculating the statistical power and various experimental parameters. Let us define

as the proportion of the phenotypic variance explained by the QTL. The squared QTL effect can be expressed as a function of h2, as shown below,

Since the squared QTL effect a2 is only meaningful when compared with σ2, we will assume σ2=1.0 in all subsequent examples.

Example 1: Calculate the statistical power at a Type I error rate α=0.01 for detecting a QTL that is located in the middle of a 20 cM marker interval and explains h2=0.10 of the phenotypic variance with n=100 F2 individuals.

We first need to find the recombination fraction between the QTL and the flanking markers using the Haldane (1919) mapping function,

We then calculate σx̂2 using equation (9),

The squared QTL effect is

The non-centrality parameter is

Corresponding to the Type I error α=0.01, the critical value for the test statistic is

The Type II error is

Therefore, the statistical power to detect such a QTL is

Since the QTL is assumed in the middle of the marker interval (the worst-case scenario), this power is an underestimation of the actual power.

Example 2: Calculate the minimum marker density required to detect a QTL explaining h2=0.10 of the phenotypic variance in an F2 mating design of n=200 individuals with γ=0.90 of the power under a Type I error rate α=0.01.

The worst-case scenario is that the QTL is located in the middle of the largest marker interval. Let D be the largest marker interval measured in centiMorgan. Assume that the recombination fraction between the QTL and each of the flanking markers is r. The recombination fraction between the two markers is r12=2r(1−r). We first calculate r using the method given below. We then get r12 and convert r12 into D to obtain the largest marker interval that allows the detection of such a QTL. Given α=0.01 and n=200, we found that

The non-centrality parameter is calculated using equation (10),

Given δ1−0.90, we can solve for σx̂2 using the inverse function of equation (7),

Using the reverse function of equation (9), we calculate

The recombination fraction between the two markers is

Finally, the size of the interval measured in cM is

Example 3: Assume that a QTL is located in the middle of a 10 cM marker interval. Calculate the minimum sample size required to detect a QTL explaining h2=0.05 of the phenotypic variance in an F2 mating design with power γ=0.80 under a Type I error rate α=0.01.

Let n be the sample size required to detect such a QTL. The distance between this QTL and each of the flanking markers is 5 cM, and thus r=0.0476 and σx̂2=0.4502. Given h2=0.05, we have a2=0.1053. Therefore, the non-centrality parameter is

Let us denote the threshold of the test statistic by

which is a function of n. We now solve the following equation with respect to n,

The solution can be found through iterations as shown below,

The final solution is n=251.7995≈252. Only seven iterations were required to converge when n(0)=100 was used as the starting value. Therefore, we need 252 individuals for the F2 family to guarantee an 80% power to detect such a QTL.

Simulation

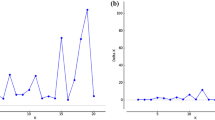
Although the theoretical power was derived based on solid statistical and mathematical foundation, it is always a good idea to verify the result via Monte Carlo simulation. We simulated a QTL located in the middle of a 20 cM interval. The flanking markers have full information. Again, we set σ2=1 so that a2=2h2/(1−h2). Two levels of h2 were used to simulate the size of the QTL, which are h2=0.05 and h2=0.10. The sample size varied from n=50 to 500 with an increment of 10. For each simulated sample, we calculated the F-test statistic. The critical values used to declare statistical significance were chosen from the central F-distributions at α=0.05. Under each situation, the simulation was replicated 1000 times. The empirical power under each specific situation was defined as the proportion of the replicates with the F-test statistics larger than the corresponding critical value. The empirical powers obtained from the simulations were compared with the theoretical powers, as illustrated by the plots given in Figure 1. The empirical powers fit the theoretical powers very closely, validating the theoretical derivation.

Figure 1
figure 1

Comparisons of the statistical powers obtained from Monte Carlo simulations (open circles and triangles) with those predicted from the theory (dotted and solid lines). The plots with open circles and solid line (upper plots) represent the situation of h2=0.10, while the plots with open triangles and dotted line (lower plots) represent the situation of h2=0.05.

Full size image

Numerical evaluation

As stated earlier, the worst situation for QTL mapping is that the QTL sits right in the middle of a marker interval. This can be verified by evaluating the power for a given QTL when the position of the QTL varies from one marker to the other marker of the interval. We assumed that the QTL explains h2=0.10 of the phenotypic variance. The sample size was n=100. The marker interval was 40 cM. The position of the simulated QTL varied from 0 cM (overlaps with the left marker) to 40 cM (overlaps with the right marker). Figure 2 represents the power change as the position of the QTL changes within the marker interval. When the QTL overlaps with a marker, the power is about 63% (the maximum value cross the interval). The lowest power is about 43%, which occurs when the QTL is located in the middle of the interval (position 20 cM).

Figure 2
figure 2

Changes of statistical power as QTL position changes from one end to the other end of a marker interval of 40 cM in length. The sample size is n=100 and the size of the QTL is h2=0.05. The lowest power occurs when the QTL is in the middle of the marker interval.

Full size image

We now assume that the QTL of interest is located in the middle of a marker interval. We then change the size of the interval from 0 cM (all three loci, two markers and a QTL, overlap) to 60 cM (the QTL is located at position 30 cM). We also allow the sample size to vary from n=50 to n=1000. We evaluated the power under two levels of the QTL size, h2=0.05 and h2=0.10. The power surfaces are plotted in the 3D graph shown in Figure 3. The following three conclusions were obtained from the result. (1) Increase of the sample size can significantly improve the statistical power. Although this conclusion is trivial, it serves as a partial validation for the formula to calculate the statistical power. When the QTL overlaps with the markers and the population is 200 or more, we will have high confidence (90%) to detect a small QTL that only contributes 5% of the phenotypic variance. (2) Change of interval size also affects the statistical power. When the interval size is increased from 0 to 60 cM, the power for detection of the same QTL is decreased from 100 to 60%. The effect of marker interval size on the power is certainly less than the effect of the sample size on the power. (3) Neither a large sample size nor a high marker density is absolutely necessary for detecting a large QTL, for example, when the QTL contributes 10% or more of the phenotype variance, the theoretical power is as high as 60% even if the QTL is in the middle of a large interval (60 cM) and only 100 individuals are used in the experiment.

Figure 3
figure 3

Change of statistical power as the sample size and marker interval change. The gray surface (upper) represents the statistical power under h2=0.10 while the surface with dark grids (lower) represents the statistical power under h2=0.05. The horizontal plane represents the power of γ=0.90.

Full size image

Discussion

Simple methods for calculating the statistical power apply to other mating designs of line crossing experiments. As long as the genotype indicator variables are defined in the same scale for all experiments, the powers can be compared. Here, we extend the power calculation to the following mating designs: BC (backcross), DH (double haploid) and RIL (recombinant inbred line). The additive genetic effect (a) in all cases is defined as the difference between two genotypes that differ by only one allele. If two genotypes differ by two alleles, the difference is expressed by 2a. Different mating designs have different powers because they have different non-centrality parameters.

BC design

There are only two genotypes, A1A1 and A1A2. Therefore, the x variable is defined as x=1/2 and x=−1/2, respectively, for the two genotypes. The true variance of x is σx2=1/2. This leads to the following variance of x̂,

where r is the recombination fraction between the QTL and a flanking marker (the QTL is in the middle of the two flanking markers).

DH design

The two genotypes in a DH family are A1A1 and A2A2. Therefore, the x variable is defined as x=1 and x=−1, respectively, for the two genotypes. The variance of x is σx2=1. The variance of x̂ is

RIL design

The two genotypes for an RIL family are A1A1 and A2A2. Therefore, the x variable is defined as x=1 and x=−1, respectively, for the two genotypes. The variance of x is σx2=1. The variance of x̂ is

Current methods for power calculation are primarily based on the assumption that the QTL overlaps with a fully informative marker (Soller et al., 1976; Muranty, 1996; Lynch and Walsh, 1998). When the QTL does not overlap a marker, that is, it is away from a marker. The power can still be calculated using the nearest marker (Soller and Genizi, 1978; Lynch and Walsh, 1998). This is a single marker analysis. However, interval mapping that uses flanking marker is more efficient than the single marker analysis, and power calculation using flanking markers has not been developed. This study explores the possibility of using a simple method to calculate the statistical power of QTL detection using flanking markers. The method has been verified using the simulated data.

The two flanking markers are assumed to be fully informative. In situations where they are not fully informative, we the estimated QTL genotype σx̂2 will be further reduced. A reduction of σ◯2 will lead to decreased power. For example, if 5% of the individuals have missing marker genotypes, the reduced variance of ◯ will be 0.05 × 0+0.95 × σ◯2=0.95σ◯2, where σ◯2 is the variance of ◯ when no missing marker genotype is assumed. The reason for this is that when an individual has missing genotypes, the variance of ◯ is zero, that is, σ◯2=0.

When genome scanning is performed, multiple tests are involved. A reasonable alpha-value for a genome-wide QTL analysis was suggested by Muranty, 1996, which is 0.001⩽α⩽0.01.

We have developed a SAS program to calculate the statistical power using the simple method. The following parameters are considered in the power calculation: the power (γ), the Type I error (α), the size of the QTL (h2), the sample size (n), the size of the marker interval (D) denoted as distance between a marker measured in cM and the type of line cross (F2, BC, DH and RIL). For a given type of line cross, the program can compute one parameter given the remaining four parameters. The program is available on request from the authors or downloadable from our website www.statgen.ucr.edu.