Abstract
In recent years, improved genotyping and sequencing technologies have enabled the discovery of new loci associated with various diseases or traits. For instance, by testing the association with each single-nucleotide variant (SNV) separately, genome-wide association studies (GWAS) have achieved tremendous success in identifying SNVs associated with specific traits. However, little is known about the common genetic basis of multiple traits owing to lack of efficient methods. With the use of extended quasi-likelihood, a Wald test has been proposed to perform a bivariate analysis of a continuous and a binary trait in unrelated samples. However, owing to its low computational efficiency, it has not been implemented in real applications to large-scale genetic studies. In this paper, we propose an efficient bivariate robust score test for two traits, one continuous and one binary, based on extended generalized estimating equations. Our approach is applicable to both family-based and unrelated study designs and can be extended to test the association of multiple traits. Our simulation studies demonstrate the type-I error rate of our approach is well controlled in all minor allele frequency (MAF) scenarios, with MAF ranging from 1 to 30%, and the method is more powerful in certain MAF scenarios than univariate testing with correction for multiple testing. Because of the computational advantage of score tests, our approach is readily applicable to GWAS or sequencing studies. Finally, we present a real application to uncover genetic variants associated with body mass index and type-2 diabetes in the Framingham Heart Study.
Similar content being viewed by others
Introduction
In recent years, univariate association test has been implemented as the predominant statistical method in genetic epidemiology and has yielded fruitful results in many applications. For example, univariate association tests have led to tremendous success in the discovery of disease susceptibility loci when applied to genome-wide association studies (GWAS) for various diseases. However, for the genetic association testing of multiple and often correlated traits, univariate association testing combined with multiple testing correction has usually been implemented owing to the ease of computation. Other variations include MultiPhen1 and Yang’s combination of univariate association tests.2 However, none of these approaches are as powerful or efficient as a joint multivariate test with each trait treated as a dependent variable in discovering genetic loci associated with all traits under study.1, 3, 4
For example, in the case of two continuous traits assumed to be normally distributed, a joint test can be derived as a simple extension of a univariate normal test. However, if one of the two traits is a discrete trait, for example, a binary trait, deriving such a test becomes challenging, and it further complicates in family samples. One reason is that there is no exact closed form of the likelihood function for a binary trait in family samples. Although applications of linear mixed effects models (LMM) have been frequently used to analyze binary traits in GWAS, researchers have demonstrated that, in the presence of relatedness, LMM results in incorrect type-I error rate owing to the violation of homoscedasticity assumption.5
Quasi-likelihood-based approaches, such as generalized estimating equations (GEE), have been proposed to address the question of correlated data.6, 7, 8 GEE has been frequently used to analyze correlated data in univariate association tests such as application to GWAS in families.9, 10 For instance, Wang et al.11 applied GEE to test gene-based and single-nucleotide variant (SNV) association with a single binary trait in family data, assuming that the working correlation matrix is a function of the relationship matrix. When treating the correlation parameters as nuisance parameters, the estimators of GEE have been shown to lack asymptotic efficiency,12 a common weakness of typical GEE approaches. An improved version of GEE was proposed by Zhao and Prentice,7, 8 in which regression parameters and correlation parameters are estimated simultaneously based on pseudo maximum-likelihood approach. However, the improved efficiency comes at the cost of having to specify a correct covariance structure, and the third and fourth moments are necessary for the estimation.8, 12
Using principles from the extended quasi-likelihood,13, 14 Hall and Severini12 established the theory of extended generalized estimating equations (EGEE). Instead of treating correlation parameters as nuisance parameters, EGEE estimates them jointly with the regression parameters and does not require correct specification of a working correlation matrix and therefore only requires up to the second order of moments. Hence, EGEE has been proven to be more powerful, more asymptotically efficient and more computer efficient than GEE while retaining many of its good properties.12
Based on the idea of EGEE, Liu et al.15 developed an approach specifically for bivariate genetic analysis. They proposed a joint Wald test to evaluate the association between a SNV and the two traits. The joint Wald test asymptotically follows a chi-squared distribution with two degrees of freedom. However, applications to large-scale genetic studies such as GWAS leads to large computational burden because the parameters have to be estimated first before constructing the test statistic each time a SNV is evaluated for association. Another limitation of EGEE application by Liu et al.15 is that it is only intended for unrelated subjects and hence is not applicable to family data. However, there has been an increasing need for methods suitable for family-based study designs because of the presence of related individuals in many existing cohorts, such as the Framingham Heart Study (FHS) and the Family Heart Study. These family-based studies have enabled the discovery of clinical and genetic risk factors influencing cardiovascular and related diseases’ risk and have made great contributions to our current understanding of several complex diseases.
In this paper, we construct a model to accommodate familial correlation, and we propose an efficient robust score test to jointly evaluate the association between a SNV and two traits, one continuous and one binary trait. Moreover, our approach has wider applicability: it can also be applied to test the association with two binary traits or a single binary trait. Our simulation studies demonstrate that the type-I error of our approach is well controlled under all minor allele frequency (MAF) scenarios down to 1% MAF. It is also shown that the score test is more powerful in certain scenarios than the univariate testing corrected for multiple testing. Finally, we present a real application to the FHS by analyzing body mass index (BMI) and type-2 diabetes (T2D) as the two traits of interest and report multiple SNV associations in or near genes with prior implication with one or both of these traits. We also report SNVs in genes that have yet to be implicated in the genetics of these traits and hence represent possible new loci. For implementation of source code, please see http://sites.bu.edu/fhspl/publications/bivaregee/.
Methods
We first state the assumptions and define the model equations for one continuous and one binary trait in family samples. We assume that there are N independent families (i=1,…, N) with a total sample size of n, and the family size (ni) depends on the family index (i). The model is composed of two simultaneous equations written as:

where the continuous trait Yc and the binary trait Yb are n × 1 vectors; Xc is the design matrix for the continuous trait-specific covariates, including an intercept, with a dimension of n × pc; βc is a pc × 1 coefficient vector for the intercept and the (pc−1) covariates; Xb is the design matrix for the binary trait-specific covariates, including the intercept, with a dimension of n × pb; βb is a pb × 1 coefficient vector for the intercept and the (pb−1) covariates; G is an n × 1 genotype vector for the SNV; βcG and βbG are the corresponding SNV coefficients for the continuous and the binary traits, respectively; and b is the random intercept following a normal distribution of  with the relationship matrix Φ being twice the kinship matrix. The vector ɛ is a random error term assumed to follow a normal distribution of
with the relationship matrix Φ being twice the kinship matrix. The vector ɛ is a random error term assumed to follow a normal distribution of  where I is the n × n identity matrix.
where I is the n × n identity matrix.
We account for within-family correlation by defining the overall variance matrix of the two traits in family blocks as  where Vi (i=1, …, N) is the variance matrix of the two traits for the ith family with a dimension of 2ni × 2ni. The within-family covariance matrix has a form
where Vi (i=1, …, N) is the variance matrix of the two traits for the ith family with a dimension of 2ni × 2ni. The within-family covariance matrix has a form  where Var(Yc i) is the covariance matrix of the continuous trait, cov(Yc i,Yb i) is the covariance matrix between the continuous and the binary trait and Var(Yb i) is the covariance matrix of the binary trait. Because the variance matrix is crucial to the parameter estimation, we further define the individual components of the variance matrix explicitly as follows:
where Var(Yc i) is the covariance matrix of the continuous trait, cov(Yc i,Yb i) is the covariance matrix between the continuous and the binary trait and Var(Yb i) is the covariance matrix of the binary trait. Because the variance matrix is crucial to the parameter estimation, we further define the individual components of the variance matrix explicitly as follows:
For the ith family, the covariance matrix of the continuous trait is expressed as

The covariance matrix of the binary trait Var(Ybi) and the covariance matrix between the continuous and the binary trait cov(Yci, Ybi) have the following forms:

where Φi (i=1, …, N) is the ith family relationship matrix with a dimension of ni × ni and Ii is the ni × ni identity matrix. We use the same working correlation matrix Ri=Φiφ (φ is an unknown parameter) as in Wang et al.11 with the diagonal elements fixed to 1. The elements of Rbc i (−1≤r≤1 is an unknown parameter) are defined as follows 

Where  is the jj′th element of the relationship matrix Φi.
is the jj′th element of the relationship matrix Φi.
Then, based on the EGEE score equations,12  , the Fisher’s scoring algorithm is implemented iteratively to update the regression parameters β=(βc, βcG, βb, βbG)T and the correlation parameters
, the Fisher’s scoring algorithm is implemented iteratively to update the regression parameters β=(βc, βcG, βb, βbG)T and the correlation parameters  until some convergence criterion is met.12, 15 The (m+1)th iteration equations are:
until some convergence criterion is met.12, 15 The (m+1)th iteration equations are:

where  D f denotes the Jacobian of f; D f=
D f denotes the Jacobian of f; D f= is the stacked matrix with a size of 2ni × (pc+pb+2);
is the stacked matrix with a size of 2ni × (pc+pb+2);  ; and σi is the vectorized Vi. We are estimating both regression parameters β and the correlation parameters α simultaneously, while in Wang’s method for a single binary trait,11 the estimates of regression parameters are first updated based on the scoring equations for β only, and the correlation parameter φ is then updated based on the formula of Pearson residuals.17 The convergence of Wang’s method is solely based on β. However, the convergence of our novel approach is based on the Euclidean distance between iterations for β, α.
; and σi is the vectorized Vi. We are estimating both regression parameters β and the correlation parameters α simultaneously, while in Wang’s method for a single binary trait,11 the estimates of regression parameters are first updated based on the scoring equations for β only, and the correlation parameter φ is then updated based on the formula of Pearson residuals.17 The convergence of Wang’s method is solely based on β. However, the convergence of our novel approach is based on the Euclidean distance between iterations for β, α.
Note that when the approach is applied to unrelated samples, it is equivalent to specifying Φi=I, φ=1,  , reducing the score equations above to the form proposed by Liu et al.15
, reducing the score equations above to the form proposed by Liu et al.15
Robust score test
Breslow18 developed a score test for overdispersed Poisson regression and other quasi-likelihood models in 1990, and then Guo et al.19 demonstrated its advantage over the sandwich estimator. Following the same rationale, we derive a robust score test to evaluate the null hypothesis of no association between the genotypes and the two traits. Equivalently, we are testing  . Note this could be easily extended to analyze two binary traits or a single binary trait.
. Note this could be easily extended to analyze two binary traits or a single binary trait.
Let  denote the vector of score function with respect to
denote the vector of score function with respect to 
 denote the vector of score function with respect to
denote the vector of score function with respect to  and let
and let  and
and  denote the parameter estimates under H0. We propose the following score test statistic:
denote the parameter estimates under H0. We propose the following score test statistic:

where  ;
;  ; U* is as previously defined; and I is the 2 × 2 identity matrix. (see Appendix for derivation details). The proposed test statistic asymptotically follows a
; U* is as previously defined; and I is the 2 × 2 identity matrix. (see Appendix for derivation details). The proposed test statistic asymptotically follows a  (termed as ‘BivarEGEE’). When the covariance structure is correctly specified,18 that is,
(termed as ‘BivarEGEE’). When the covariance structure is correctly specified,18 that is,  , the variance formula of U(2) will reduce to
, the variance formula of U(2) will reduce to  (the subscript 1 and 2 corresponds to θ(1) and θ(2), respectively). The test statistic with this restriction is termed as ‘BivarEGEER’.
(the subscript 1 and 2 corresponds to θ(1) and θ(2), respectively). The test statistic with this restriction is termed as ‘BivarEGEER’.
Simulations
We conduct simulation studies to evaluate the validity of our approach to test the association between SNVs with different MAF and two traits. We also compare the power of our approach to a univariate approach to determine under which circumstances it is more powerful.
Type-I error
We compare the type-I error rate of our approach to the minimum P-value obtained from the univariate association testing for each trait with Bonferroni correction for multiple testing of two traits (‘minP’). We simulate the traits under the null hypothesis that there is no genetic association with any of the two traits, that is,  . We simulate 8 SNV scenarios with MAF ranging from 0.01 to 0.3. For each SNV and trait scenario, we simulate 50 000 replicates and calculate the proportion of simulations reaching the significance threshold of 0.001. In each replicate, we simulate a total of 1000 independent nuclear families with 2 parents and the number of children randomly determined from a discrete uniform distribution ranging from 1 to 4, so that family size ranges from 3 to 6 members. Within each family, we simulate the genotypes of the parents under Hardy–Weinberg equilibrium, and the children’s genotypes using random allele dropping. We also simulate two covariates: age and sex. Given a family, the sex of the offspring is randomly assigned and we simulate age in the following way: we first simulate the age of the youngest adult offspring from a continuous uniform distribution ranging from 30 to 50, additional offspring’s ages are set to be within 5 years of the first one with at least a 1-year gap so that the possibility of them being twins is excluded. The mother is assumed to be 20–45 years older than all her offspring, and the father’s age is set to be within 5-year of the mother’s age and he must be at least 20 years older than his oldest offspring. We then simulate two continuous traits influenced by age and sex only, based on the following two equations, so that age and sex explains around 4.5 and 5.4% of the total variance of y1 versus 11 and 0.9% of y2:
. We simulate 8 SNV scenarios with MAF ranging from 0.01 to 0.3. For each SNV and trait scenario, we simulate 50 000 replicates and calculate the proportion of simulations reaching the significance threshold of 0.001. In each replicate, we simulate a total of 1000 independent nuclear families with 2 parents and the number of children randomly determined from a discrete uniform distribution ranging from 1 to 4, so that family size ranges from 3 to 6 members. Within each family, we simulate the genotypes of the parents under Hardy–Weinberg equilibrium, and the children’s genotypes using random allele dropping. We also simulate two covariates: age and sex. Given a family, the sex of the offspring is randomly assigned and we simulate age in the following way: we first simulate the age of the youngest adult offspring from a continuous uniform distribution ranging from 30 to 50, additional offspring’s ages are set to be within 5 years of the first one with at least a 1-year gap so that the possibility of them being twins is excluded. The mother is assumed to be 20–45 years older than all her offspring, and the father’s age is set to be within 5-year of the mother’s age and he must be at least 20 years older than his oldest offspring. We then simulate two continuous traits influenced by age and sex only, based on the following two equations, so that age and sex explains around 4.5 and 5.4% of the total variance of y1 versus 11 and 0.9% of y2:

where  , the additive covariance matrix is
, the additive covariance matrix is  and the environmental covariance matrix is
and the environmental covariance matrix is  .
.
We transform y2 to a binary variable using a threshold model with a disease prevalence of 30%, assuming a disease with a high prevalence such as obesity or hypertension in older adults. Based on the same trait and covariates data set, in each replicate, we compute the ‘minP’ as follows: we conduct univariate association testing on y1 and the transformed binary version of y2, select the smaller P-value, and then multiply it by a factor of 2 (Bonferroni’s correction). In both approaches, the type-I error rate is defined as the proportion of replicates with P-value<0.001.
Power simulation
We compare the power of our approach to the minimum P-value obtained from univariate tests (minP) under the same scenarios (Table 1) and the same family structure as above. In addition to the effects of sex and age, we include an additively coded genetic variant to the model, so that the traits are simulated under the alternative hypothesis that there is an association between the genotypes and each of the two traits:

where m is used to model the relative strength of association and takes values of −0.5, −0.1, 0.1 and 0.5 under different scenarios; and ɛ1 and ɛ2 follow the same normal distribution as for the type-I error simulations. We adjust the correlation parameter ρ (=0.2, 0.5 or 0.8) in the additive covariance matrix  to reflect different correlation magnitude between the two traits. We set Σe equal to Σa, except in the last two scenarios (the bottom row in Figure 1), where the covariance term in Σe is set to be negative.
to reflect different correlation magnitude between the two traits. We set Σe equal to Σa, except in the last two scenarios (the bottom row in Figure 1), where the covariance term in Σe is set to be negative.
Power (y axis) as a function of MAF (x axis). Different trait correlation (ρ) values are distinguished by different color lines, and different effect size proportion (m) are presented in each panel: (a) m=−0.1; (b) m=−0.5; (c) m=−0.5 (negative environmental covariance); (d) m=0.1; (e) m=0.5; (f) m=−0.5 (negative environmental covariance).
For each scenario, we simulate 1000 replicates and then compute the power as the proportion of simulations reaching the significance threshold of 0.0001, a threshold that gives a good range of power for the methods compared.
Framingham Heart Study
One important motivation for developing the model and proposing the score test statistic is to provide a computationally efficient approach applicable to large-scale genetic studies such as GWAS, exome sequencing or whole genome sequencing (WGS) studies. In the application section, we perform a genome-wide association of BMI and T2D in the FHS, to better understand the common genetic basis of these two traits.
The FHS was initiated in 1948 and is a longitudinal study consisting of three generations of cohorts: the Original cohort, the Offspring cohort and the third generation (Gen 3) cohort, totaling 14, 428 participants. Some participants were recruited from the same household, and hence are related. Over the years, research efforts in FHS have been rewarded with fruitful results in identifying risk factors of cardiovascular-related traits such as blood pressure and cholesterol levels, as well as glycemic and other metabolic traits.
Obesity is an important risk factor in the development of T2D.20, 21 By applying our approach to BMI, a continuous variable, and T2D, a binary variable, on a genome-wide scale, we hope to better understand their common genetic basis. In our analyses, both traits are adjusted for age and sex.
We analyze the association between these two traits and genotypes from the Framingham SNP Health Association Resource (SHARe) project sponsored by the National Heart, Lung and Blood Institute (NHLBI). Genotypes from Affymetrix 500K genotyping arrays (Affymetrix, Santa Clara, CA, USA), supplemented by the Affymetrix MIPS array, were available on 8481 participants after exclusion for low call rate (<97%), heterozygosity rate outside of 5 SDs from the mean or excess Mendelian errors (>1000). Additional SNVs were imputed with the software MACH (Markov Chain-based haplotyper) using the HapMap 2 reference haplotypes.22
Results
Type-I error
Simulation results show that the type-I error rate of our proposed approach (‘BivarEGEE’) is well controlled in all MAF scenarios where MAF ranges from 0.01 to 0.3 (Table 1). We also provide the type-I error rate when the variance structure is assumed to be correctly specified (‘BivarEGEER’). The fact that both approaches yield the same type-I error rate in all MAF scenarios is a good indication that the variance structure is correctly modeled. The type-I error rate of the minP approach is also well controlled at α=0.001.
Power simulations
The results of power simulations are presented in Figure 1. The results suggest that when the two untransformed traits have opposite direction of association with the SNV, our proposed approach is consistently more powerful. The highest power gain from BivarEGEE over minP reaches 40%. In the scenarios where both traits have the same direction of association, the power gain differs depending on the relative association strength m and the correlation ρ. For instance, when m=0.1, BivarEGEE is more powerful or as powerful as minP when the two untransformed traits are strongly or moderately correlated (ρ=0.8 or 0.5), while the power slightly decreases when the two traits have a weak correlation (ρ=0.2). When m=0.5, BivarEGEE is at least as powerful as minP when the two traits have a weak or moderate correlation, while with increased correlation, the power tends to suffer some small loss. When the covariance term of the environmental covariance matrix Σe is set to be negative, our approach is consistently more powerful for common variants (MAF>0.02).
Application to the FHS
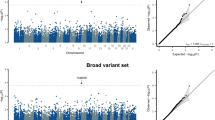
We apply our approach to study the genome-wide association between genetic variants from the Framingham SHARe and the combination of BMI and T2D status in FHS participants. A total of 7038 genotyped and phenotyped participants in 1185 families are analyzed after participants with missing traits or without genotypes are omitted. Both traits are adjusted for age and sex. We present the genome-wide association results as the minus logarithm base 10 of the P-value in Figure 2 and also provide a list of the top 20 SNVs with the smallest P-values in Table 2. Three SNVs reach the GWAS significance threshold of 5 × 10−8, including the top 2 SNVs from chromosome 4, near the height-associated gene HHIP.23 The chromosome 4-associated SNVs are also near TMEM154, a T2D-associated gene identified by the DIAbetes Genetics Replication And Meta-analysis (DIAGRAM) Consortium in 2014.24
Among the remaining top 20 SNVs, chromosome 16 SNVs (rs8059849, rs9931529, rs13332434, rs9783765) are near FTO, a gene known for its association with both BMI and T2D.24, 25, 26, 27, 28, 29 The SNV rs10894188 (chromosome 11) is near MTNR1B, a gene known to be associated with both T2D and obesity-related traits;26 rs12097783 (chromosome 1) is near previously identified BMI gene SEC16B;29, 30, 31, 32 rs11145958 (chromosome 9) is near GPSM1, a T2D-associated gene;33 5 SNVs on chromosome 1 are near NOTCH225 and ADAM30,25 two genes known for SNVs associated with T2D; rs17863929 (chromosome 4) is approximately 3 Mb away from IL2,34 a gene known for SNVs in the intron region associated with type-1 diabetes.
Discussion
We propose a novel approach to test the association between a genetic variant and two traits, at least one of which is binary, in family samples, based on EGEE. Our approach can handle a range of families, including large and complex pedigrees. Using simulation studies, we demonstrate that our approach has well-controlled type-I error rate in all the scenarios evaluated and is more powerful than univariate tests adjusted for multiple testing in certain scenarios.
Our approach is based on extended quasi-likelihood. Fisher’s scoring algorithm is implemented for parameter estimation. It is worth noting that we model the covariance matrix of the binary and continuous traits as a function of the kinship matrix. Moreover, we propose to use a conditional correlation matrix to account for the correlation between the two traits, which is novel. All these features lead to a computer-efficient implementation that allows for genome-wide applications. In the simulation studies, our unrestricted approach (‘BivarEGEE’) has similar type-I error rate as the restricted version (‘BivarEGEER’), so we are confident that the covariance structure is correctly modeled in our approach. However, ‘BivarEGEE’ is more flexible, because it has no additional restrictions on the covariance structure of the traits. Using a similar framework, our approach can be easily extended to the analysis of two binary traits or a single binary trait, for which R functions and sample codes are also available on the webpage. The approach should readily be extendable to genetic analysis of three or four traits simultaneously. However, extensions to >4 traits might add complexity to the model and implementation.
Although our approach is based on joint estimation and testing, it is computer efficient. Table 3 lists computing time when applied to data with different family structure and sample size, including parameter estimation under the null hypothesis, computing the test statistic and P-value on a single node of Intel(R) Xeon(R) CPU E5-2640 0 @ 2.50 GHz Linux machine. As a score test, the parameter estimation is performed only once under the null hypothesis prior to application to a large-scale genetic study, such as GWAS. The computational time for minP is also listed in Table 3. It takes approximately half the time to analyze a single binary trait compared with that to analyze the two traits jointly. The time it takes to analyze a continuous trait using famskat35 increases exponentially with the sample size. By contrast, it is not computationally affordable to apply the Wald test proposed by Liu et al.15 to a large-scale genetic study, because the parameters always have to be re-estimated each time a new SNV is tested for association.
Bivariate genetic association testing is not new, but it has not been extensively applied, due to various limitations or non-availability of the existing methods and software. In this paper, we develop a bivariate approach, BivarEGEE, and we apply our approach to a real data set and found interesting associations. For instance, we replicate some loci close to relevant genes known to have impact on both traits, such as FTO and MTNR1B. One novel region (chr1:115,259,019-115,262,711 using GRCh38) on chromosome 1 was among our top findings; however, no prior T2D or BMI associations have been reported in this region. Replication from an independent study using our approach or other multivariate methods is needed to determine whether this finding is spurious or a real replicable association that we have identified using BivarEGEE and would have been undetectable without a powerful bivariate analytic approach. It is worth noting that our approach is not purely driven by the more significantly associated trait. For example, rs1558902 (FTO, chromosome 16) is the most significantly associated SNV with BMI (P=2.6 × 10−9) but is not associated with T2D (P=0.20). The overall P-value of rs1558902 with both traits (P=1.7 × 10−6) does not reach the GWAS significance threshold.
Current GWAS often involve meta-analysis of independent studies in a consortium, because meta-analysis can greatly increase sample size and power. In the future, we aim to develop meta-analysis method for the BivarEGEE approach. This will provide a more powerful bivariate approach to study two traits that commonly occur in human physiology and disease and offers a powerful approach to identify novel SNV associations with multiple correlated traits.
References
O’Reilly PF, Hoggart CJ, Pomyen Y et al: MultiPhen: joint model of multiple phenotypes can increase discovery in GWAS. PLoS One 2012; 7: e34861.
Yang Q, Wu H, Guo C, Fox CS : Analyze multivariate phenotypes in genetic association studies by combining univariate association tests. Genet Epidemiol 2010; 34: 444–454.
Lange C, Van Steen K, Andrew T et al: A family-based association test for repeatedly measured quantitative traits adjusting for unknown environmental and/or polygenic effects. Stat Appl Genet Mol Biol 2004; 3: 1–27.
Klei L, Luca D, Devlin B, Roeder K : Pleiotropy and principal components of heritability combine to increase power for association analysis. Genet Epidemiol 2008; 32: 9–19.
Chen H, Wang C, Conomos MP et al: Control for population structure and relatedness for binary traits in genetic association studies via logistic mixed models. Am J Hum Genet 2016; 98: 653–666.
Zeger SL, Liang K, Albert PS : Models for longitudinal data: a generalized estimating equation approach. Biometrics 1988; 44: 1049–1060.
Prentice RL, Zhao LP : Estimating equations for parameters in means and covariances of multivariate discrete and continuous responses. Biometrics 1991; 47: 825–839.
Zhao LP, Prentice RL : Correlated binary regression using a quadratic exponential model. Biometrika 1990; 77: 642–648.
Kathiresan S, Manning AK, Demissie S et al: A genome-wide association study for blood lipid phenotypes in the Framingham Heart Study. BMC Med Genet 2007; 8: 1.
Levy D, Larson MG, Benjamin EJ et al: Framingham Heart Study 100K project: Genome-wide associations for blood pressure and arterial stiffness. BMC Med Genet 2007; 8: 1.
Wang X, Lee S, Zhu X, Redline S, Lin X : GEE-Based SNP set association test for continuous and discrete traits in family-based association studies. Genet Epidemiol 2013; 37: 778–786.
Hall DB, Severini TA : Extended generalized estimating equations for clustered data. J Am Stat Assoc 1998; 93: 1365–1375.
Nelder JA, Pregibon D : An extended quasi-likelihood function. Biometrika 1987; 74: 221–232.
McCullagh P, Nelder JA : Generalized Linear Models. CRC Press, 1989; Vol 37.
Liu J, Pei Y, Papasian CJ, Deng H : Bivariate association analyses for the mixture of continuous and binary traits with the use of extended generalized estimating equations. Genet Epidemiol 2009; 33: 217–227.
Hall DB : On the application of extended quasi-likelihood to the clustered data case. Can J Stat 2001; 29: 77–97.
McCullagh P, Nelder JA, McCullagh P : Generalized Linear Models. London: Chapman and Hall, 1989; Vol 2.
Breslow N : Tests of hypotheses in overdispersed Poisson regression and other quasi-likelihood models. J Am Stat Assoc 1990; 85: 565–571.
Guo X, Pan W, Connett JE, Hannan PJ, French SA : Small-sample performance of the robust score test and its modifications in generalized estimating equations. Stat Med 2005; 24: 3479–3495.
Chan JM, Rimm EB, Colditz GA, Stampfer MJ, Willett WC : Obesity, fat distribution, and weight gain as risk factors for clinical diabetes in men. Diabetes Care 1994; 17: 961–969.
Colditz GA, Willett WC, Stampfer MJ et al: Weight as a risk factor for clinical diabetes in women. Am J Epidemiol 1990; 132: 501–513.
Li Y, Willer CJ, Ding J, Scheet P, Abecasis GR : MaCH: using sequence and genotype data to estimate haplotypes and unobserved genotypes. Genet Epidemiol 2010; 34: 816–834.
Lango Allen H, Estrada K, Lettre G et al: Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature 2010; 467: 832–838.
DIAbetes Genetics Replication And Meta-analysis (DIAGRAM) Consortium Asian Genetic Epidemiology Network Type 2 Diabetes (AGEN-T2D) Consortium South Asian Type 2 Diabetes (SAT2D) Consortium: Genome-wide trans-ancestry meta-analysis provides insight into the genetic architecture of type 2 diabetes susceptibility. Nat Genet 2014; 46: 234–244.
Zeggini E, Scott LJ, Saxena R et al: Meta-analysis of genome-wide association data and large-scale replication identifies additional susceptibility loci for type 2 diabetes. Nat Genet 2008; 40: 638–645.
Voight BF, Scott LJ, Steinthorsdottir V et al: Twelve type 2 diabetes susceptibility loci identified through large-scale association analysis. Nat Genet 2010; 42: 579–589.
Perry JR, Voight BF, Yengo L et al: Stratifying type 2 diabetes cases by BMI identifies genetic risk variants in LAMA1 and enrichment for risk variants in lean compared to obese cases. PLoS Genet 2012; 8: e1002741.
Willer CJ, Speliotes EK, Loos RJ et al: Six new loci associated with body mass index highlight a neuronal influence on body weight regulation. Nat Genet 2009; 41: 25–34.
Berndt SI, Gustafsson S, Magi R et al: Genome-wide meta-analysis identifies 11 new loci for anthropometric traits and provides insights into genetic architecture. Nat Genet 2013; 45: 501–512.
Wen W, Zheng W, Okada Y et al: Meta-analysis of genome-wide association studies in east asian-ancestry populations identifies four new loci for body mass index. Hum Mol Genet 2014; 23: 5492–5504.
Monda KL, Chen GK, Taylor KC et al: A meta-analysis identifies new loci associated with body mass index in individuals of african ancestry. Nat Genet 2013; 45: 690–696.
Speliotes EK, Willer CJ, Berndt SI et al: Association analyses of 249,796 individuals reveal 18 new loci associated with body mass index. Nat Genet 2010; 42: 937–948.
Hara K, Fujita H, Johnson TA et al: Genome-wide association study identifies three novel loci for type 2 diabetes. Hum Mol Genet 2014; 23: 239–246.
Barrett JC, Clayton DG, Concannon P et al: Genome-wide association study and meta-analysis find that over 40 loci affect risk of type 1 diabetes. Nat Genet 2009; 41: 703–707.
Chen H, Meigs JB, Dupuis J : Sequence kernel association test for quantitative traits in family samples. Genet Epidemiol 2013; 37: 196–204.
Acknowledgements
This work was supported by the National Heart, Lung and Blood Institute's Framingham Heart Study (Contract No. N01-HC-25195 & HHSN268201500001I) and its contract with Affymetrix, Inc for genotyping services (Contract No. N02-HL-6-4278), and by grants from the National Institute of National Institute for Diabetes and Digestive and Kidney Diseases (NIDDK) R01 DK078616, NIDDK K24 DK080140 and American Diabetes Association Mentor-Based Postdoctoral Fellowship Award #7-09-MN-32.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Appendix
Appendix
Below we show how the coefficient matrix A of the score function is derived.
Let U(3) denote the score function vector with respect to the correlation parameter vector α, and U(1), U(2) is as defined in the methods section. We apply the first-order Taylor expansion around α, θ(1) and  to the score function vector
to the score function vector  , substitute the estimates from Fisher’s algorithm
, substitute the estimates from Fisher’s algorithm  ,
,  ,
,  at H0 and thus we obtain the following equations:
at H0 and thus we obtain the following equations:

Using the principle of Fisher’s scoring algorithm by replacing the second-order derivative with its expectation, we get

Next we substitute these equations into the equation for the first-order Taylor expansion of U(2) around α, θ(1) and  and replace the first-order derivative by its expectation to obtain the following equation evaluated at:
and replace the first-order derivative by its expectation to obtain the following equation evaluated at:

Hence  .
.
Rights and permissions
About this article
Cite this article
Wang, S., Meigs, J. & Dupuis, J. Joint association analysis of a binary and a quantitative trait in family samples. Eur J Hum Genet 25, 130–136 (2017). https://doi.org/10.1038/ejhg.2016.134
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/ejhg.2016.134