Abstract
Recent advances in next-generation sequencing (NGS) make it possible to directly sequence genomes and exomes of individuals with Mendelian diseases and screen sequence data for causal variants. With the reduction in cost of NGS, DNA samples from entire families can be sequenced and linkage analysis can be performed directly using NGS data. Inspired by ‘burden’ tests, which are used for complex trait rare variant association studies, we developed the collapsed haplotype pattern (CHP) method for linkage analysis. Using data from several deafness genes we demonstrate that the CHP method is substantially more powerful than analyzing individual variants. Unlike applying NGS data filtering approaches, the CHP method provides statistical evidence of a gene’s involvement in disease etiology and is also less likely to exclude causal variants in the presence of phenocopies and/or reduced penetrance. The CHP method was implemented in the SEQLinkage software package, which can perform linkage analysis on NGS data or can generate data compatible with many linkage analysis programs, reviving them for use in NGS era.
Similar content being viewed by others
Introduction
The advent and advance of next-generation sequencing (NGS) in recent years has led to the identification of a large number of Mendelian disease genes. The typical approach to identify Mendelian disease causal variants using either whole genome sequence or whole exome sequence (WES) data is to filter variants in an affected individual or shared by affected family members, excluding those that are found at higher frequencies, for example, >0.5% in variant databases. Sometimes unaffected family member(s) are also used in the filtering process. Although filtering is straightforward and has been successful,1 such efforts rely on limited family information, for example, mode of inheritance, sharing between a subset of family members and information from external resources on variant functional characterizations and frequencies. On the other hand, linkage analysis, which incorporates information on mode of inheritance, penetrance, allele frequencies and genetic map information, remains a powerful tool to localize Mendelian disease loci. As a result, combined SNP array-based linkage analysis and sequence-based filtering method is becoming popular.2 There is also a great interest to directly perform linkage analysis on rare variants obtained from NGS data. Although it has been shown that analyzing rare single-nucleotide variants (SNVs), usually designated as having a minor allele frequency (MAF) <0.5% or 1%, from NGS data provides acceptable linkage results, due to low heterozygosity of SNVs and allelic heterogeneity this approach can be less powerful than analysis of SNPs from genotyping arrays.3
Here we describe the collapsed haplotype pattern (CHP) method, which is motivated by rare variant association methods that analyze multiple rare variants within a region, which is often a gene. The CHP method was designed to analyze rare variants by constructing markers that have a higher heterozygosity and are more informative for linkage analysis than individual rare SNVs. Unlike multipoint linkage methods, the CHP method does not require linkage disequilibrium (LD) pruning to avoid spurious associations.4 The CHP method is particularly powerful in the presence of intra- (eg, compound heterozygotes) and inter-family allelic heterogeneity, a phenomenon commonly observed for Mendelian diseases. When causal variants are missing from samples, the CHP method can still detect linkage owing to transmission information retained by other variants. We have developed the SEQLinkage software package implementing the CHP method. As SEQLinkage can calculate Heterogeneity LOD (HLOD) scores the CHP method remains powerful when there is locus heterogeneity, that is, the underlying genetic etiology is not due to the same gene/region in all families.
Materials and methods
For the CHP method instead of analyzing each variant separately, multiple variants which form haplotypes within a genetic region, for example gene, are analyzed. This is done by constructing a marker, which reflects the transmission pattern of the entire region and is numerically compatible with currently available linkage analysis methods and software. These markers incorporate allelic heterogeneity between and within families in a region and often have higher heterozygosity than SNVs, making them more informative and powerful to detect linkage.
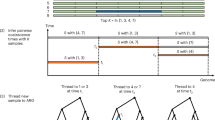
To generate regional markers, haplotypes for the region must be obtained for all samples with sequence data. NGS data from family members are first checked for Mendelian errors and variants with Mendelian inconsistencies are removed. An improved version of the Lander–Green algorithm for genetic phasing is applied to reconstruct haplotypes in the pedigrees.5 For each pedigree, we first cluster variants on regional haplotypes by ‘bins’, for example, LD blocks, and collapse variants in a bin into an indicator variable with values 0 or 1 for having no minor allele or at least one minor allele within the bin, which is similar to collapsing methods for rare variant association analysis.6 We then assign each collapsed haplotype a single numeric value so that different patterns of collapsed haplotypes in each pedigree are uniquely represented (Figure 1). The choice of coding for patterns are arbitrary, although we use continuous positive integers and assign a smaller value for collapsed haplotypes having more 0’s than 1’s. The sample haplotypes thus represented can be directly used for parametric linkage analysis with many existing linkage software packages.
Coding of regional markers using the Collapsed Haplotype Pattern (CHP) method. Three two-generational autosomal recessive pedigrees display the coding for a regional marker using information from six variant sites. Panel a shows two families segregating the same autosomal recessive disease, which is due to different causal variants. Treating the entire region as a bin to collapse the variants effectively captures transmission of disease variants and allows for linkage information for a region to be summed across families. For regions with more diverse rare variant architecture as displayed in panel b, where for this example disease etiology is caused by compound heterozygotes variants, coding which represents both rare variant haplotypes is used to ensure that all meioses are informative. It should be noted that if coding as is shown in panel a is used in this situation there will be a loss of information because all heterozygous offspring will be uninformative for linkage information, for example, the meioses to offspring II:1 and II:4.
For WES data, genes can be used as regional markers. Within each region, commonly used bin size options for variants collapsing are (1) LD-based collapsing, which uses estimated LD blocks as bins, (2) complete collapsing, where the bin size equals gene/region length and (3) no collapsing, where the bin size equals one. For regions where recombination events occur within a family, the sub-unit that shows the strongest evidence of linkage among all sub-units created by recombination breakpoints is used as the regional LOD score for the family, so that results from multiple families can still be combined.
To reconstruct genotypes for family members missing sequence data, linkage analysis requires marker allele frequencies. Frequencies of regional markers generated by CHP method can be derived from MAFs of variants and pair-wise LD between variants. For rare variants with MAF derived from large samples (see Discussion), the minor allele counts can be approximated by a multivariate Poisson distribution with joint probability mass function P(X)=f(λ,θ)(X) where λM × 1 is expected allele counts for M variants and θM × M is the variance–covariance matrix.7 The covariance between variants Xi and Xj can be computed by  where
where  is the LD coefficient, p is population MAF and N is the sample size, based on which population MAF are estimated. Therefore, for a given haplotype pattern xH=[x1, x2,…,xM], xk∈{0,1} the corresponding frequency f(λ,θ)(X=xH) can be computed from the probability mass function. When collapsing is applied, MAF for the collapsed unit is given as 1−f(λ,θ)(X=[0,0,0,…]) by definition. CHP frequencies thus computed are then used as the allele frequencies for the corresponding regional genotype markers.
is the LD coefficient, p is population MAF and N is the sample size, based on which population MAF are estimated. Therefore, for a given haplotype pattern xH=[x1, x2,…,xM], xk∈{0,1} the corresponding frequency f(λ,θ)(X=xH) can be computed from the probability mass function. When collapsing is applied, MAF for the collapsed unit is given as 1−f(λ,θ)(X=[0,0,0,…]) by definition. CHP frequencies thus computed are then used as the allele frequencies for the corresponding regional genotype markers.
To facilitate linkage analysis using sequence data in VCF format, we developed the SEQLinkage software that uses the Elston–Stewart algorithm as incorporated in FASTLINK.8 It provides results in text format and high-quality graphical reports for both LOD and HLOD scores. In addition, SEQLinkage supports output of regional genotype data into formats compatible with linkage software such as LINKAGE9 and Merlin,10 with which two-point and multipoint parametric linkage analysis can be performed. In addition, MEGA211 format is supported, which can be used to transform data to the required input for a number of linkage programs.
To evaluate performance of our method we performed empirical type I error and power calculations for two-point linkage analysis using data on four non-syndromic hearing impairment (NSHI) genes: two autosomal recessive genes GJB2 and SLC26A4, and two autosomal dominant genes MYO7A and MYH9. Two-generation pedigrees were simulated, with three to eight offspring in the last generation with the proportions determined by the distribution of number of children per family in the United States in 2012, rescaled so that they sum to 100% (three children: 69.34%, four children: 20.52%, five children: 6.84%, six children: 2.28%, seven children 0.76%, eight children 0.26%). Genotypes are simulated for the four genes based on the variant sites and the corresponding MAFs in European Americans recorded in the Exome Variant Server.
For type I error evaluations, we use the same gene sequences and demographic data, yet simulate disease pedigrees under the null, that is, affection status not due to any of the rare variants in the gene of interest. We consider different genetic architectures under the null including situations when (1) variants in the gene region are in linkage equilibrium, (2) there is complete LD between variants and (3) there exist within a gene recombination events in the sequence data of generated families. Recombination events between variants are simulated based on rates obtained from Hapmap Recombination Rates and Hotspots database (see Web Resources). In addition, we simulate scenarios when parental genotypes are missing to evaluate type I error when CHP marker frequencies have to be calculated using population MAF and LD estimated from data. Type I errors are computed for cumulative HLOD scores on gene SLC26A4 across 20 families using 2 000 000 replicates.
For power evaluations we annotate variants in these four NSHI genes using Deafness Variation Database (DVD) and NCBI ClinVar, labeling variants as ‘causal’ if they are so deemed by both databases. Disease status for individuals are determined by genotypes on those causal sites under dominant mode of inheritance for MYO7A and MYH9, and recessive (compound heterozygotes and homozygotes) for GJB2 and SLC26A4, assuming complete penetrance. In addition, for each mode of inheritance we allow for allelic heterogeneity among families, that is, the causal variant site in a gene may not be the same for different families. We ‘ascertain’ simulated families having two or more affected offspring for linkage analysis. To introduce locus heterogeneity we sample families having causal variants in one gene but not the other, so that each simulated gene contributes to etiology of only a proportion of families in the entire data set. We simulate 500 replicates under each different setting of sample size, mode of inheritance, presence of allelic heterogeneity and locus heterogeneity. For each replicate we compute LOD and HLOD scores using the CHP method. For comparison purposes we also analyze SNV markers and perform multipoint linkage analysis using GeneHunter.12 Power is estimated by  where the denominator is the total number of replicates and the numerator is the number of tests that successfully detected the linkage signal, that is, LOD score >3.3 or HLOD score >3.6, which provides a genome-wide significance level of P<0.05.13
where the denominator is the total number of replicates and the numerator is the number of tests that successfully detected the linkage signal, that is, LOD score >3.3 or HLOD score >3.6, which provides a genome-wide significance level of P<0.05.13
Results
Empirical type I error for the CHP linkage statistic is  , (95% CI: 2.11 × 10−5 ≤α≤3.63 × 10−5), demonstrating that type I error is well controlled and even conservative at a required significance level of 4.7 × 10−5 for an HLOD of 3.6. Quantile–quantile plots are generated to evaluate the null distribution of test statistic in the presence of within-gene recombination, strong inter-marker LD and missing genotype data; type I error is well controlled and no sign of inflation is observed (Supplementary Figure S1). Empirical power calculations for several known non-syndromic hearing impairment genes using the CHP method as well as for individual SNVs are summarized by contour plots (Figure 2). Power analysis based on LOD and HLOD suggests that CHP is substantially more powerful for all models in the presence of intra- (Figure 2c) and inter-family allelic heterogeneity (Figures 2a–c). For example to detect linkage with the SLC26A4 gene using an autosomal recessive model with allelic heterogeneity, that is, compound heterozygotes, and also with locus heterogeneity of 50%, 12 families are required for the CHP method to achieve a power of 90%, while analyzing individual SNVs requires >50 families to achieve the same power at a genome-wide significance level of 0.05. In addition, although multipoint linkage analysis is more powerful than analyzing SNVs, the CHP method is considerably more powerful than multipoint linkage analysis (Supplementary Table S1).
, (95% CI: 2.11 × 10−5 ≤α≤3.63 × 10−5), demonstrating that type I error is well controlled and even conservative at a required significance level of 4.7 × 10−5 for an HLOD of 3.6. Quantile–quantile plots are generated to evaluate the null distribution of test statistic in the presence of within-gene recombination, strong inter-marker LD and missing genotype data; type I error is well controlled and no sign of inflation is observed (Supplementary Figure S1). Empirical power calculations for several known non-syndromic hearing impairment genes using the CHP method as well as for individual SNVs are summarized by contour plots (Figure 2). Power analysis based on LOD and HLOD suggests that CHP is substantially more powerful for all models in the presence of intra- (Figure 2c) and inter-family allelic heterogeneity (Figures 2a–c). For example to detect linkage with the SLC26A4 gene using an autosomal recessive model with allelic heterogeneity, that is, compound heterozygotes, and also with locus heterogeneity of 50%, 12 families are required for the CHP method to achieve a power of 90%, while analyzing individual SNVs requires >50 families to achieve the same power at a genome-wide significance level of 0.05. In addition, although multipoint linkage analysis is more powerful than analyzing SNVs, the CHP method is considerably more powerful than multipoint linkage analysis (Supplementary Table S1).
Power comparisons for LOD and HLOD statistics in two-point linkage analyses. This figure shows the power for collapsed haplotype pattern markers (CHP) vs single-nucleotide variant (SNV) analysis under various modes of inheritance in the presence of intra- and inter-family allelic heterogeneity. X axis is number of families, Y axis is proportion of locus heterogeneity, that is, the proportion of families with non-syndromic hearing impairment (NSHI) caused by detrimental variants in the gene under investigation, that is, either MYO7A or MYH9 for dominant model, or GJB2 or SLC26A4 for recessive model. Contour curves on the graphs are power estimates, dark orange lines for the CHP method and light blue lines for SNV analysis. Panel a displays the power for the LOD and HLOD statistics under an autosomal dominant model; panel b displays the power for the LOD and HLOD statistics under an autosomal recessive model; panel c displays the power for the LOD and HLOD statistics under an autosomal recessive model in the presence of intra-family allelic heterogeneity, that is, affected individuals are compound heterozygous. CHP method is more powerful for both LOD and HLOD at a genome-wide significance level of α=0.05, but the absolute power of HLOD is not significantly larger than LOD. This is due to the very low MAFs for the genes under study, and therefore, for most families all variants in the non-causal gene are monomorphic and, therefore, are uninformative.
For sequence data, variants are sometimes missing due to the inability to call variants or during quality control, variant calls are removed because of poor data quality. Therefore, we also estimated sample size requirements for the CHP method when causal variants are missing from sequence data in a large proportion of families, that is, 75%. The CHP method can tolerate missing data and is also always more powerful than the SNV method when there is missing data (Table 1).
Discussion
For linkage analysis, correct specification of marker allele frequency is crucial for controlling type I error and reducing type II error.14 The number of founders with available genotypes in data for linkage analysis might often be too small to obtain a sufficiently accurate allele frequency estimate, thus we recommend the input VCF file be annotated with an external source of MAF information, for example, 1000 Genomes or Exome Variant Server. For some populations MAF information may not be available and frequencies estimated from founders have to be used.
In the context of Mendelian disease gene mapping it is often reasonable to assume that common variants (variants having population MAF >1%) are not causal. Common variants will neither contribute to nor reduce power when analyzed with rare variants. However, common variants can be in strong LD with variants in neighboring regions, which may contain causal variants; thus, when the CHP method is used to construct the regional marker also using common variants, linkage can be detected even though the region does not harbor any causal variants. Although common variants should not be used when constructing regional markers, we suggest analyzing common variants separately because they can potentially capture additional information when rare causal variants are missing from sequence data.
Analysis of rare variants using ‘burden’ methods are usually limited to those variants, which are most likely to be causal, for example, missense, nonsense and splice site variants, because inclusion of non-causal variants can attenuate the association signal and reduce power. For the CHP methods inclusion of non-causal rare variants will not attenuate the linkage signal and therefore analysis does not need to be restricted to variants that are most likely functional and causal. Inclusion of non-causal rare variants to construct the regional marker can provide additional linkage information if data for causal variants are missing. If the goal is to detect a linkage signal from variants that are potentially causal then linkage analysis using the CHP method can be limited to those variants which are most likely functional.
In addition to being more powerful than performing multipoint linkage analysis, the CHP method also controls type I error when there is missing parental genotype data and inter-marker LD, which is not the case for multipoint linkage analysis. Caution should be used when performing multipoint linkage analysis on sequence data, as when parental genotypes are missing for some samples (common for NGS-based family data) variants in LD can lead to severe inflated type I error when markers are assumed to be in linkage equilibrium.15, 16 The majority of multipoint linkage analysis programs, for example, GeneHunter, SuperLink,17 Vitesse18 do not take into consideration LD between marker loci. Even for linkage programs that can model inter-marker LD, for example, LINKAGE/FASTLINK and Merlin, the haplotype frequency estimates involving rare variants can be inaccurate for studies with limited number of founders, leading to inflated type I error.
The SEQLinkage package, freely available at URL http://bioinformatics.org/seqlink, can efficiently extract genotypes from VCF files and uses the CHP method described here to perform linkage analysis as well as data format conversion on sequence data so that other programs can also be used to perform linkage analysis if desired. It provides a novel and effective approach that brings back well-established linkage analysis techniques for use with the growing wealth of genomic data of human pedigrees. Unlike filtering approaches that are commonly used to analyze sequence data, SEQLinkage provides statistical evidence of the involvement of variants in the etiology of Mendelian diseases. In addition, because it incorporates mode of inheritance information and penetrance models it is less likely than filtering approaches to exclude causal variants in the presence of phenocopies and/or reduced penetrance. For Mendelian traits for which the penetrance model is not well established but the mode of inheritance is known, an affected-only analysis can be performed where all unaffected individuals are made unknown to avoid decreased power due the use of an incorrect penetrance model. We recommend the use of SEQLinkage in parallel with filtering methods on the same sequence data to take full advantage of the power of NGS in families.
References
Ng SB, Buckingham KJ, Lee C et al: Exome sequencing identifies the cause of a mendelian disorder. Nat Genet 2010; 42: 30–35.
Santos-Cortez RLP, Lee K, Azeem Z et al: Mutations in KARS, encoding lysyl-tRNA synthetase, cause autosomal-recessive nonsyndromic hearing impairment DFNB89. Am J Hum Genet 2013; 93: 132–140.
Smith KR, Bromhead CJ, Hildebrand MS et al: Reducing the exome search space for Mendelian diseases using genetic linkage analysis of exome genotypes. Genome Biol 2011; 12: R85.
Huang Q, Shete S, Amos CI : Ignoring linkage disequilibrium among tightly linked markers induces false-positive evidence of linkage for affected sib pair analysis. Am J Hum Genet 2004; 75: 1106–1112.
Abecasis GR, Wigginton JE : Handling marker-marker linkage disequilibrium: pedigree analysis with clustered markers. Am J Hum Genet 2005; 77: 754–767.
Li B, Leal SM : Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am J Hum Genet 2008; 83: 311–321.
Karlis D : An EM algorithm for multivariate Poisson distribution and related models. J Appl Stat 2003; 30: 63–77.
Cottingham RW Jr, Idury RM, Schäffer AA : Faster sequential genetic linkage computations. Am J Hum Genet 1993; 53: 252–263.
Lathrop GM, Lalouel JM, Julier C, Ott J : Strategies for multilocus linkage analysis in humans. Proc Natl Acad Sci 1984; 81: 3443–3446.
Abecasis GR, Cherny SS, Cookson WO, Cardon LR : Merlin—rapid analysis of dense genetic maps using sparse gene flow trees. Nat Genet 2002; 30: 97–101.
Mukhopadhyay N, Almasy L, Schroeder M, Mulvihill WP, Weeks DE : Mega2: data-handling for facilitating genetic linkage and association analyses. Bioinformatics 2005; 21: 2556–2557.
Kruglyak L, Daly MJ, Reeve-Daly MP, Lander ES : Parametric and nonparametric linkage analysis: a unified multipoint approach. Am J Hum Genet 1996; 58: 1347–1363.
Lander E, Kruglyak L : Genetic dissection of complex traits: guidelines for interpreting and reporting linkage results. Nat Genet 1995; 11: 241–247.
Freimer NB, Sandkuijl LA : Blower SM. Incorrect specification of marker allele frequencies: effects on linkage analysis. Am J Hum Genet 1993; 52: 1102–1110.
Huang Q, Shete S, Swartz M, Amos CI : Examining the effect of linkage disequilibrium on multipoint linkage analysis. BMC Genet 2005; 6: S83.
Li B, Leal SM : Ignoring intermarker linkage disequilibrium induces false-positive evidence of linkage for consanguineous pedigrees when genotype data is missing for any pedigree member. Hum Hered 2008; 65: 199–208.
Fishelson M, Geiger D : Exact genetic linkage computations for general pedigrees. Bioinformatics 2002; 18 (Suppl 1): S189–S198.
O’Connell JR, Weeks DE : The VITESSE algorithm for rapid exact multilocus linkage analysis via genotype set-recoding and fuzzy inheritance. Nat Genet 1995; 11: 402–408.
Acknowledgements
The authors would like to thank Regie Lyn Santos-Cortez, Daniel Weeks, Alejandro Schaffer, Jeffrey O’Connell and Jurg Ott for helpful discussions and support. This work is funded by National Institute of Health (DC003594, DC011651 and HG006493). Web Resources: America's Families and Living Arrangements, https://www.census.gov/prod/2013pubs/p20-570.pdf. Exome Variant Server, http://evs.gs.washington.edu/EVS. DVD, http://deafnessvariationdatabase.com. NCBI ClinVar, https://www.ncbi.nlm.nih.gov/clinvar. Hapmap Recombination Rates and Hotspots database, http://hapmap.ncbi.nlm.nih.gov/downloads/recombination/latest/rates/.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies this paper on European Journal of Human Genetics website
Supplementary information
Rights and permissions
About this article
Cite this article
Wang, G., Zhang, D., Li, B. et al. Collapsed haplotype pattern method for linkage analysis of next-generation sequence data. Eur J Hum Genet 23, 1739–1743 (2015). https://doi.org/10.1038/ejhg.2015.64
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/ejhg.2015.64
This article is cited by
-
Identification of autosomal recessive nonsyndromic hearing impairment genes through the study of consanguineous and non-consanguineous families: past, present, and future
Human Genetics (2022)
-
A quantitative trait rare variant nonparametric linkage method with application to age-at-onset of Alzheimer’s disease
European Journal of Human Genetics (2020)
-
A powerful new method for rare-variant analysis of quantitative traits in families
European Journal of Human Genetics (2020)
-
Exome genotyping and linkage analysis identifies two novel linked regions and replicates two others for myopia in Ashkenazi Jewish families
BMC Medical Genetics (2019)
-
Small posterior fossa in Chiari I malformation affected families is significantly linked to 1q43-44 and 12q23-24.11 using whole exome sequencing
European Journal of Human Genetics (2019)