Abstract
The last decade of human genetic research witnessed the completion of hundreds of genome-wide association studies (GWASs). However, the genetic variants discovered through these efforts account for only a small proportion of the heritability of complex traits. One explanation for the missing heritability is that the common analysis approach, assessing the effect of each single-nucleotide polymorphism (SNP) individually, is not well suited to the detection of small effects of multiple SNPs. Gene set analysis (GSA) is one of several approaches that may contribute to the discovery of additional genetic risk factors for complex traits. Complex phenotypes are thought to be controlled by networks of interacting biochemical and physiological pathways influenced by the products of sets of genes. By assessing the overall evidence of association of a phenotype with all measured variation in a set of genes, GSA may identify functionally relevant sets of genes corresponding to relevant biomolecular pathways, which will enable more focused studies of genetic risk factors. This approach may thus contribute to the discovery of genetic variants responsible for some of the missing heritability. With the increased use of these approaches for the secondary analysis of data from GWAS, it is important to understand the different GSA methods and their strengths and weaknesses, and consider challenges inherent in these types of analyses. This paper provides an overview of GSA, highlighting the key challenges, potential solutions, and directions for ongoing research.
Similar content being viewed by others
Introduction
Over the last decade, hundreds of genome-wide association studies (GWASs) for complex human traits were completed1(http://www.genome.gov/gwastudies/). Yet to date, the genetic variants discovered by GWAS, based primarily on univariate analyses of individual single-nucleotide polymorphisms (SNPs), account for only a small proportion of the heritability of complex traits.2, 3 One possible explanation for the ‘missing heritability’ is that the analysis strategy commonly used in GWAS, testing for association of the phenotype with each SNP individually, is not well suited for detecting multiple variants with small effects.4 Proposed research strategies to uncover the missing heritability include studying rare variants and structural variation, as well as epistatic and epigenetic effects.2 Secondary analyses of GWAS data using novel statistical methods such as gene set analysis (GSA) have also been proposed as a way to extract additional information from genome-wide SNP data.5 GSA aims to assess the overall evidence of association of variation in an entire set of genes with a phenotype, such as disease status or a quantitative trait.6, 7 A gene set (GS) is a pre-defined set of genes based on criteria other than the data currently being analyzed. For example, genes within a specific biological pathway defined in the Kyoto Encyclopedia of Genes and Genomes (KEGG) database (http://www.genome.jp/kegg/pathway.html) can constitute a GS. Although the terms GSA and pathway analysis are often used interchangeably, we use the term GSA to refer to an analysis of a set of genes, which does not model specific relationships among genes within the GS. We reserve the term pathway analysis for analyses that incorporate information on the relationships among genes within the GS, and/or model the relationships among the genes.8, 9
GSA has the potential to detect subtle effects of multiple SNPs in the same GS that might be missed when assessed individually.7 Because numerous genes can be combined into a limited number of GSs for analysis, the multiple testing burden may be greatly reduced by GSA. Moreover, the incorporation of biological knowledge in the statistical analysis may aid researchers in the interpretation of results.6
GSA methods were first introduced in the context of gene expression (microarray) data analysis10, 11, 12 but have since been extended to other data types, in particular to SNP data from GWAS.13, 14, 15 GSA for GWAS has recently been used to investigate many common diseases including breast cancer,16 Alzheimer's disease,17 multiple sclerosis,18 bone mineral density,19 hypertension, type 1 and 2 diabetes, and coronary artery disease.20 Such studies are leading to novel insights into the etiology of common diseases and possible relationships between diseases that were not detected using the individual SNP analysis approach. For example, PGE2 and calcium signaling GSs were recently implicated in both hypertension and Crohn's disease,20 indicating a possible connection between these two complex diseases.
With the accumulation of knowledge of biological processes that impact complex traits and the genes that influence these processes, GSA is becoming a common approach for analysis of genetic and molecular data.6, 7 With the increased use of GSA for GWAS, it is important to carefully consider the benefits and drawbacks of GSA, compare the different GSA methods, and address challenges inherent in these types of analyses. This paper provides an overview of GSA and describes the key challenges and unresolved issues, potential solutions, and directions for ongoing research. Although some of the discussed issues apply to all types of GSA, the primary focus is on issues that arise in GSA involving SNP data from GWAS.
The GSA hypothesis: competitive vs self-contained methods
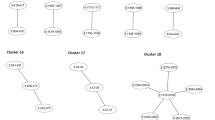
GSA methods can be divided into two types: competitive and self-contained.11 Many competitive methods are based on first identifying SNPs (or genes) that are significantly associated with a trait, and then evaluating whether the significantly associated SNPs tend to cluster in predefined GSs. These methods are competitive because they compare the frequency of significantly associated SNPs in a particular set of genes with the frequency of significant associations among all genes not in the set. The null hypothesis for competitive methods is Ho: SNPs/genes in the GS of interest are associated with the phenotype as much as SNPs/genes outside the GS. The commonly used GS enrichment analysis (GSEA), originally proposed by Subramanian et al10 and later extended to GWAS by Wang et al,14 is a competitive method that assesses the enrichment of significant associations for genes in the GS (as compared with those outside the GS) using a weighted Kolmogorov–Smirnov running-sum statistic. Another commonly used approach for competitive GSA uses the Fisher's exact test to compare the proportion of associations exceeding some pre-specified significance threshold within the GS, to the proportion of such signals outside the GS13, 21, 22 (see Figure 1 for examples of competitive testing using Fisher's exact test). One important limitation of Fisher's exact test, and similar methods, is the dichotomization of SNP association results into significant and nonsignificant based on a pre-defined significance level, which ignores information regarding the strength of the association.
In contrast to competitive methods, self-contained methods only consider results within a GS of interest to test the null hypothesis Ho: SNPs/genes in the GS of interest are not associated with the phenotype vs the alternative hypothesis Ha: SNPs/genes in the GS are associated with the phenotype. Figure 2 shows a simple example of a self-contained GSA based on the Fisher's exact test. For comparison with the example of competitive GSA shown in Figure 1 example A, the same data for the GS of interest are used. In this study, however, the self-contained null hypothesis is tested by assessing the deviation from the expected number of significant SNPs under the hypothesis of no association of the phenotype with the GS. Dichotomization of results into ‘significant’ or ‘not significant’ based on a P-value threshold is not necessary when testing the self-contained GSA hypothesis. Self-contained GSA can also be based on computing association P-values for each SNP in a GS, followed by testing whether the observed distribution of the SNP-specific P-values deviates from the expected distribution under the null hypothesis of no association. Finally, joint modeling of the effects of SNPs in a GS can also be used for a self-contained GSA.
It is important to recognize that competitive and self-contained methods test different hypotheses, and key differences between these two approaches stem from the difference in the null hypothesis. Although sample-level permutation is appropriate for the estimation of empirical P-values when testing the null hypothesis of self-contained methods, for the null hypothesis tested by competitive methods procedures based on permutation of genes between GSs are needed to determine the null distribution.23 One limitation of competitive GSA methods is that they cannot be applied to studies of candidate GSs for which only SNPs in the candidate GS have been genotyped. Self-contained methods, on the other hand, can be used for genome-wide studies as well as candidate GS studies.
Because of these fundamental differences between competitive and self-contained methods, the appropriate approach should be selected based on a thoughtful consideration of the null and alternative hypotheses the researcher is interested in testing, and constraints imposed by the available data (eg, genotypes limited to a candidate pathway, or genome-wide data with unaccounted for genome-wide inflation of association statistics).
GS definition
GSs are collections of genes with related function or characteristics. For example, GSs can be identified from manually drawn pathway maps representing molecular interaction and reaction networks.24 GSs can be identified based on other criteria, such as a pre-specified region of the genome or similarity of function (eg, genes involved in DNA repair). A growing number of publically available resources provide descriptions of pathways, along with lists of genes that contribute to the processes making up these pathways. Pathguide (http://www.pathguide.org)25 lists over 300 databases of information related to pathways, demonstrating the challenge of selecting a pathway resource. Several of these pathway resources, including the KEGG (http://www.genome.jp/kegg/),24 the Gene Ontology project (http://www.geneontology.org/),26 MetaCore (http://www.genego.com/metacore.php), and BioCarta (http://www.biocarta.com/genes/index.asp), are commonly used. Specialized pathway resources, such as the Pharmacogenetics and Pharmacogenomics Knowledge Base for pharmacogenomic pathways (http://www.pharmgkb.org/), are also available. Additional information on pathway resources and GS definition can be found in Bader et al,25 Bard and Rhee,27 and Viswanathan et al.28
When defining GSs for analysis, it is important to clearly state the scope of a GS, realizing that knowledge about the genome and definitions of GSs are evolving and that no single definition of a GS exists.27 Care should be taken in selecting a reliable ontology resource, as some resources are based on more rigorous curating of GSs (eg, KEGG), whereas others provide more complete listings of biological pathways (eg, MetaCore). Finally, it is important to recognize that current coverage of genes (and thus GSs) is not uniform, as the coverage of genes by SNPs on GWAS arrays is not uniform. This problem will diminish with the development of denser genome-wide SNP arrays, or with use of genotype imputation methods.29 However, at this point, interpretation of GS results should take into account coverage limitations for GSs of interest.
Once a set of genes is defined, questions remain regarding which SNPs should be included in the analysis of the GS. A commonly used approach is to include any SNP known to map to any gene or within a given distance of any gene, in the GS. Although it is not obvious how far up and downstream of each gene should be included in the mapping of SNPs to genes, ideally, the regulatory region(s) of each gene should be included and perhaps even regions in LD with any portion of the gene. Smith et al30 reported that the degree of disequilibrium for markers separated by ∼30 kb in a Caucasian population was similar to the degree of disequilibrium between markers separated by ∼10 kb in an African population, with the average level of LD decaying to less than r2=0.10 after 50 kb. On the basis of these considerations, SNPs within 20–50 kb from the first and last exon should be included as part of a gene for GSA to cover the regulatory regions of the gene, as well as SNPs in LD with the gene.
Currently GSs usually consist of SNPs in, or near, genes thought to contribute to a particular biological process. However, the definition of a GS could be extended to use other knowledge related to gene function. For example, mRNA expression data has been used by Zhong et al31 to define GSs that include eSNPs, that is, SNPs that have been shown to regulate the expression of a particular gene in either a cis- or trans-acting manner. Recent advances in molecular genetics provide novel insight into the relationships between genetic variation and variation in mRNA expression leading to the identification of eQTLs at an unprecedented level.32 eSNPs can be defined based on study specific expression data or information from publically available databases (see eg, http://scan.bsd.uchicago.edu/newinterface/about.html33 and http://eqtl.uchicago.edu/Home.html,32, 34).
Analytical approaches
A variety of GSA approaches have been proposed for genome-wide expression studies, and subsequently modified for genome-wide SNP studies (see Table 1). In the following sections we discuss various aspects of GSA, noting the limitations and relative merits of different types of approaches. The features of GSA that we focus on include the strategy for taking into account gene-level association; statistical method (methods based on combining measures of association of the phenotype with each SNP/gene and methods based on joint modeling of the genotypic data); impact of LD and gene size; and effect of population stratification.
The strategy for taking into account gene-level association: one-step vs two-step methods
In terms of whether or not gene-level evidence of association is considered when aggregating the evidence for association in a GS, two approaches can be considered: (1) a ‘two-step’ approach in which SNPs in each gene are first used to evaluate association with the gene, followed by aggregation of the gene-level tests to test for association of the phenotype with the GS; and (2) a ‘one-step’ approach in which all SNPs in a GS are used in the analysis without consideration of gene-level effects.
For the two-step GSA many different methods can be used to assess the association of the phenotype with the gene before determining the association of the GS with the phenotype. Options include using the minimum SNP-specific P-value for a gene, using a summary measure of all individual SNP P-values within the gene, or simultaneously modeling the effects of all SNPs in the gene on the phenotype. Many GSA methods applied to GWAS data have used a two-step approach taking the minimum P-value observed for the SNPs in a gene (or maximum test statistic) as the gene-level evidence of association. However, this approach must account for the fact that a larger gene with more SNPs is likely to have a smaller minimum P-value as compared with a smaller gene with fewer SNPs. In addition, when each of several SNPs in a gene has a modest effect on the phenotype, using the minimum P-value may not be the most powerful approach. Numerous studies have assessed the performance of various multimarker methods for testing the association of a gene with a complex trait,35, 36, 37 which may provide guidance for the completion of a two-step GSA. Principal component analysis has been shown to be a powerful approach for conducting gene-level association testing,36, 37 and thus is a reasonable choice for gene-level association testing for GSA.
Both the one-step and two-step approaches have advantages and disadvantages. For a given study, the most powerful GSA method depends on the underlying disease-causing mechanism which is unknown. Nevertheless, an understanding of which method is most powerful for detection of particular types of disease-causing models can be used to guide choice of analysis method and interpretation of results. Yu et al38 presented a GSA method that relies on an adaptive rank truncated product method and compared results between a two-step and a one-step GSA. In their comparison, they found neither the two-step nor the one-step analysis dominated in terms of power. Studies are underway to determine which approach is more powerful under a variety of genetic models, with some results indicating that in general the two-step approach may be more powerful than the one-step approach when the self-contained GS hypothesis is assessed.
Although both one- and two-step methods may be considered for GSA, based on the biological relevance of genes and the need to account for LD between SNPs within the same gene, two-step approaches which first assess association of each gene with the phenotype, followed by testing association between the phenotype and the GS, may be preferred. The use of two-step approaches aids in the interpretation of GSA results, as key genes associated with the phenotype can be identified.
Statistical method: P-value or test statistic combination vs joint modeling
GSA methods can also be classified based on how evidence of association is aggregated across SNPs in a GS: P-values or test statistics of individual SNPs (or genes) can be combined to form a test statistic, or effects of all the SNPs can be modeled jointly. With the first of these approaches, GSA is performed by testing for association of each SNP with the phenotype, followed by combining the evidence of association (eg, P-values) across the GS. Among such methods, Fisher's method, as well as extensions and modifications of Fisher's method, have been proposed for gene-level tests of associations and for GSA.39, 40, 41, 42 When the number of markers is large, variations of Fisher's method that use only markers with P-values less than a pre-specified significance level,41 or the top K markers (based on P-value), referred to as the ‘rank truncated product method’,43 are more powerful than Fisher's method based on all P-values.
Rather than combining measures of association of individual SNPs/genes, GSA can also be based on modeling the joint effects of SNPs in a GS. Although joint modeling of SNP effects across genes has practical limitations, it is certainly feasible within a gene, as part of a two-step GSA. The effects of all SNPs within the gene may be jointly modeled using multiple linear or logistic regression. However, this approach may lack power, and the model may become non-estimable if the number of SNPs exceeds the number of subjects. Shrinkage and variable selection methods, both frequentist and Bayesian, have been proposed to model the association of a phenotype with multiple SNPs in a gene. These methods are more adept to handling the high-dimensional aspect of genomic data and the multicollinearity caused by LD among SNPs.44, 45, 46, 47
Data reduction based analytical methods, such as principal components and kernels, can also be used for either a one-step or two-step GSA. Research assessing methods for multiple SNP analysis has indicated that principal components and a global model with random effects tend to have the highest power across a variety of scenarios involving a modest number of markers (10–40 markers).36, 37 Some benefits of the principal component approach include reduction of the model degrees of freedom and easy implementation in most statistical software packages for a variety of phenotypes without the requirement for determining haplotype phase. However, it has been shown that when there is a large number of markers (>100), the truncated Fisher's method (with empirical P-values) out-performs principal components35 for multi-marker association analysis. In contrast to principal component analysis, which uses a linear reduction method, kernel methods for gene-level analysis48, 49 have a benefit in that they can apply either linear or nonlinear dimension reduction.
Some of the methods previously proposed for conducting gene-level association tests as part of a two-step GSA can also be used in a one-step GSA procedure. In particular, the approaches that can be applied when the number of variables (ie, SNPs) is large compared with the sample size, such as shrinkage and dimension reduction methods, can also be used to jointly model the association with all SNPs in a GS (one-step approach). Evaluation of alternative statistical methods for SNP-based GSA is a topic of ongoing research.
Impact of LD and size of GS: assessment of GS association significance by permutation
Owing to LD between SNPs within the same GS, independence between markers cannot be assumed in the assessment of significance of the GS. Instead, for statistical approaches that assume independence of markers for computation of distribution (asymptotic) based GS P-values, permutation or Monte Carlo methods50 should be used to determine an empirical P-value for GS association. Permutation methods can also correct for size of the GS and potential bias introduced by GSA methods based on, for example, the minimum P-value or maximum test statistic for SNPs in a gene. This bias arises because of the fact that genes with more SNPs are likely to have smaller minimum P-values as compared with genes with fewer SNPs; ignoring this ‘size’ bias can lead to inflated type 1 error rates in testing for GS association.14, 51
To select an appropriate permutation procedure, the null and alternative hypotheses of interest and the GSA method being applied must be carefully considered. Permutations appropriate for various self-contained GSA methods have been described, for example by Fridley et al,52 whereas Efron and Tibshirani23 addressed the issue of permutation for competitive GSA. Although these permutation procedures were described in the context of GSA for gene expression data, similar procedures are applicable to SNP data.
One important benefit of modeling approaches for GSA is that often these methods do not require independence between SNPs within the GS removing the burden of permutations. In contrast, methods based on combining P-values or test statistics often assume independence of P-values and thus permutation methods are required to obtain valid genes set P-values and correct type I error rates. Two-step approaches can consist of jointly modeling the SNP effects within a gene followed by combining gene-level P-values to test for association with the GS. Although much less correlation is expected between the gene-level P-values, a non-negligible level of correlation between genes in a GS may exist. Thus permutation methods are still recommended for these types of analyses, in particular to verify any significant results.
Population stratification: impact on analysis of individual SNPs vs impact on GSA
The potential effects of population stratification on GWAS have been discussed extensively.53 However, it is worth noting that population stratification, and similar sources of confounding, can have a much more profound impact on the results of GSA, as a small inflation of many SNP association statistics may result in significant GS associations. GSA methods are designed to detect the cumulative effect of many SNPs with weak association with the phenotype. Thus, if association test statistics for many SNPs in the GS are slightly inflated, for example, because of population stratification, a significant GS association test may result. This can lead to highly inflated, false-positive rates for GSA, particularly for large GSs, when self-contained approaches based on P-value combination methods are applied.
In comparison with self-contained methods, competitive GSA methods are expected to be more robust to the effects of population stratification and similar sources of confounding, such as differential genotyping errors between cases and controls.54 This is because if the effects of population stratification have the same impact on every GS, the effects would essentially cancel out. However, this argument assumes that the effect of population stratification is the same across GSs. This may not be the case. For example, GSs that represent essential cellular processes may be highly conserved between populations, and show little differences in terms of allele frequencies. Meanwhile, GSs corresponding to pathways involved in response to environmental stimuli may show more differentiation between populations, and may thus have greater population structure. Thus, both self-contained and competitive GSA should carefully account for effects of population stratification.
Power of GSA
One motivation for GSA is the potential increase in power to detect genetic associations of the phenotype with a GS, as compared with the power to detect association with individual SNPs. Factors that affect power for detecting association with a given SNP include: allele frequency, sample size, prevalence of the disease, significance level (accounting for multiple testing), and effect size. It is believed that many rare SNPs, or SNPs with small effects, contribute to complex traits; yet their effects are not detectable with the commonly applied approach of testing each SNP individually followed by correction for multiple comparisons. The power of GSA depends on factors such as the number and size of effects within a GS, the minor allele frequencies for the causal SNPs, the size of the GS, and the number of GSs tested.
It is hoped that GSA will provide greater power to detect genetic effects than analysis of all SNPs individually. As the number of GSs is substantially smaller than the number of SNP markers on GWAS arrays, fewer hypotheses will be tested in GSA, requiring less stringent multiple testing correction. Moreover, by aggregating many SNPs with weak associations, evidence of association at the GS level may emerge, even when the analysis of individual SNPs failed to discover any significantly associated genetic variants. For example, a GSA of hypertension discovered numerous statistically significant GSs, such as the dopamine signaling pathway, while the original single SNP analysis, completed by the Wellcome Trust Case Control Consortium, lacked significant findings.20
Discussion
GSA is becoming a commonly applied approach for secondary analysis of GWAS data. Key benefits of GSA include the reduction in multiple testing and the incorporation of previous biological knowledge into the analysis. The accumulation of small effects of many genetic variants into a single analysis of the GS is expected to be more powerful than tests that individually assess the association of the phenotype with each genetic variant. We have summarized the key aspects of GSA that researchers need to consider when performing GSA for a complex trait. The first, and possibly most important, is the selection of an analysis method that matches the scientific hypothesis of interest (ie, competitive or self-contained) and the interpretation of findings in the context of this hypothesis. Following the selection of the null hypothesis of interest, the next steps of a GSA involve the definition of GSs and mapping of SNPs to genes within these GSs; and the selection of a powerful analytical approach for conducting the GSA that accounts for LD and gene size, and incorporates the necessary adjustment for population stratification. If a GS is shown to be associated with a phenotype, further investigation should assess the relationships between the SNPs and genes within the GS to reveal the biological relationships that regulate the pathways linking genotypes to phenotypes.
Although GSA has numerous benefits, this type of analysis also has limitations that might hinder the success of some studies. Gaps in knowledge may prevent definition of appropriate GSs, and combining a few genes with functional impact on the phenotype with many non-associated genes can lead to loss of power. The fact that GSA assumes that SNPs can be assigned to relevant genes is an important limitation, particularly in light of the fact that many disease-associated SNPs identified to date do not lie in genes. Extending the GS definition to include eQTLs (SNPs that regulate expression of relevant genes) may reduce the impact of this problem. GSA methods that can incorporate multiple data types, including mRNA expression data, epigenetic data, and environmental data, also need to be developed. Xiong and colleagues recently introduced software for combining mRNA gene expression data and SNP data into a GSEA (http://gsaa.genome.duke.edu/).
Although GSA attempts to investigate the overall evidence of association with variation in a set of related genes, most GSA methods, in particular those based on combination of individual SNP P-values, still fail to account for joint effects that are not because of simple additive (or log additive) effects of individual SNPs. Methods based on joint modeling of SNP effects could be extended to include assessment of gene–gene interactions. Investigation of gene–gene interactions in the context of a GS, as opposed to genome wide, would greatly reduce the number of possible two-way interactions and may aid in the interpretation of the results. Herold et al55 and Zamar et al56 recently proposed the use of biological information to guide gene–gene interaction analysis, and implemented their approaches in the software INTERSNP (http://intersnp.meb.uni-bonn.de/) and PATH (http://genapha.icapture.ubc.ca/PathTutorial/), respectively. The proposed methods include assessing interactions between all pairs of non-synonymous SNPs or analyzing all combinations of three SNPs that lie in a common pathway. Further research and development of methods to assess interactions within GSs is warranted.
GSA could also be extended to include rare variants. Two-step approaches that assess the evidence of association at the gene level before evaluating association with the GS are particularly conducive to the inclusion of rare variants, as most rare variant analyses focus on gene level tests by collapsing the effects of all rare SNPs in a gene into a single test of association. Finally, establishment of standards for replication of findings from GSA, and measures of the GS ‘effect size’ (eg, population attributable risk) would aid researchers in the interpretation of GSA findings.
GSA is a compelling approach for analysis of complex genetic data. Although these methods are not designed to identify specific genes or genetic variations that are associated with the trait of interest, results from a GSA can be used to plan further, in-depth, investigation focused on specific GSs of interest with novel technologies that may uncover additional genetic causes of complex traits. Similar to all other genetic analysis approaches, GSA alone will not resolve all remaining questions regarding genetic etiology of complex traits, or find all of the ‘missing heritability’ of these traits. Rather, it should serve as one of many complementary tools that will contribute to knowledge of the genetic basis for the development of complex phenotypes. The hope is that by following up GSA results, scientists will gain insight into the complex relationship between genomic variation and the clinical phenotype.
References
Hindorff LA, Sethupathy P, Junkins HA et al: Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc Natl Acad Sci USA 2009; 106: 9362–9367.
Eichler EE, Flint J, Gibson G et al: Missing heritability and strategies for finding the underlying causes of complex disease. Nat Rev 2010; 11: 446–450.
Manolio TA, Collins FS, Cox NJ et al: Finding the missing heritability of complex diseases. Nature 2009; 461: 747–753.
Hirschhorn JN, Daly MJ : Genome-wide association studies for common diseases and complex traits. Nat Rev 2005; 6: 95–108.
Cantor RM, Lange K, Sinsheimer JS : Prioritizing GWAS results: a review of statistical methods and recommendations for their application. Am J Hum Genet 2010; 86: 6–22.
Wang K, Li M, Hakonarson H : Analysing biological pathways in genome-wide association studies. Nat Rev 2010; 11: 843–854.
Holmans P : Statistical methods for pathway analysis of genome-wide data for association with complex genetic traits. Adv Genet 2010; 72: pp 141–179.
Conti DV, Cortessis V, Molitor J et al: Bayesian modeling of complex metabolic pathways. Hum Hered 2003; 56: 83–93.
Ideker T, Thorsson V, Ranish JA et al: Integrated genomic and proteomic analyses of a systematically perturbed metabolic network. Science 2001; 292: 929–934.
Subramanian A, Tamayo P, Mootha VK et al: Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci USA 2005; 102: 15545–15550.
Goeman JJ, Buhlmann P : Analyzing gene expression data in terms of gene sets: methodological issues. Bioinformatics 2007; 23: 980–987.
Allison DB, Cui X, Page GP et al: Microarray data analysis: from disarray to consolidation and consensus. Nat Rev 2006; 7: 55–65.
Holmans P, Green EK, Pahwa JS et al: Gene ontology analysis of GWA study data sets provides insights into the biology of bipolar disorder. Am J Hum Genet 2009; 85: 13–24.
Wang K, Li M, Bucan M : Pathway-based approaches for analysis of genomewide association studies. Am J Hum Genet 2007; 81: 1278–1283.
Chen LS, Hutter CM, Potter JD et al: Insights into colon cancer etiology via a regularized approach to gene set analysis of GWAS data. Am J Hum Genet 2010; 86: 860–871.
Menashe I, Maeder D, Garcia-Closas M et al: Pathway analysis of breast cancer genome-wide association study highlights three pathways and one canonical signaling cascade. Cancer Res 2010; 70: 4453–4459.
Lambert JC, Grenier-Boley B, Chouraki V et al: Implication of the immune system in alzheimer's disease: evidence from genome-wide pathway analysis. J Alzheimers Dis 2010; 20: 1107–1118.
Baranzini SE, Galwey NW, Wang J et al: Pathway and network-based analysis of genome-wide association studies in multiple sclerosis. Hum Mol Genet 2009; 18: 2078–2090.
Zhang L, Guo YF, Liu YZ et al: Pathway-based genome-wide association analysis identified the importance of regulation-of-autophagy pathway for ultradistal radius BMD. J Bone Miner Res 2010; 25: 1572–1580.
Torkamani A, Topol EJ, Schork NJ : Pathway analysis of seven common diseases assessed by genome-wide association. Genomics 2008; 92: 265–272.
O’Dushlaine C, Kenny E, Heron EA et al: The SNP ratio test: pathway analysis of genome-wide association datasets. Bioinformatics 2009; 25: 2762–2763.
Medina I, Montaner D, Bonifaci N et al: Gene set-based analysis of polymorphisms: finding pathways or biological processes associated to traits in genome-wide association studies. Nucleic Acids Res 2009; 37: W340–W344.
Efron B, Tibshirani R : On testing the significance of sets of genes. Ann Appl Stat 2007; 1: 107.
Kanehisa M, Goto S : KEGG: kyoto encyclopedia of genes and genomes. Nucleic Acids Res 2000; 28: 27–30.
Bader GD, Cary MP, Sander C : Pathguide: a pathway resource list. Nucleic Acids Res 2006; 34: D504–D506.
Ashburner M, Ball CA, Blake JA et al: Gene ontology: tool for the unification of biology. The gene ontology consortium. Nat Genet 2000; 25: 25–29.
Bard JB, Rhee SY : Ontologies in biology: design, applications and future challenges. Nat Rev 2004; 5: 213–222.
Viswanathan GA, Nudelman G, Patil S et al: BioPP: a tool for web-publication of biological networks. BMC Bioinformatics 2007; 8: 168.
Marchini J, Howie B : Genotype imputation for genome-wide association studies. Nat Rev 2010; 11: 499–511.
Smith AV, Thomas DJ, Munro HM et al: Sequence features in regions of weak and strong linkage disequilibrium. Genome Res 2005; 15: 1519–1534.
Zhong H, Yang X, Kaplan LM et al: Integrating pathway analysis and genetics of gene expression for genome-wide association studies. Am J Hum Genet 2010; 86: 581–591.
Pickrell JK, Marioni JC, Pai AA et al: Understanding mechanisms underlying human gene expression variation with RNA sequencing. Nature 2010; 464: 768–772.
Gamazon ER, Zhang W, Konkashbaev A et al: SCAN: SNP and copy number annotation. Bioinformatics 2010; 26: 259–262.
Veyrieras JB, Kudaravalli S, Kim SY et al: High-resolution mapping of expression-QTLs yields insight into human gene regulation. PLoS Genet 2008; 4: e1000214.
De la Cruz O, Wen X, Ke B et al: Gene, region and pathway level analyses in whole-genome studies. Genet Epidemiol 2010; 34: 222–231.
Ballard DH, Cho J, Zhao H : Comparisons of multi-marker association methods to detect association between a candidate region and disease. Genet Epidemiol 2010; 34: 201–212.
Gauderman WJ, Murcray C, Gilliland F et al: Testing association between disease and multiple SNPs in a candidate gene. Genet Epidemiol 2007; 31: 383–395.
Yu K, Li Q, Bergen AW et al: Pathway analysis by adaptive combination of P-values. Genet Epidemiol 2009; 33: 700–709.
Whitlock MC : Combining probability from independent tests: the weighted Z-method is superior to Fisher's approach. J Evol Biol 2005; 18: 1368–1373.
Zaykin DV, Zhivotovsky LA, Czika W et al: Combining P-values in large-scale genomics experiments. Pharm Stat 2007; 6: 217–226.
Zaykin DV, Zhivotovsky LA, Westfall PH et al: Truncated product method for combining P-values. Genet Epidemiol 2002; 22: 170–185.
Chai HS, Sicotte H, Bailey KR et al: GLOSSI: a method to assess the association of genetic loci-sets with complex diseases. BMC Bioinformatics 2009; 10: 102.
Dudbridge F, Koeleman BP : Rank truncated product of P-values, with application to genomewide association scans. Genet Epidemiol 2003; 25: 360–366.
Malo N, Libiger O, Schork NJ : Accommodating linkage disequilibrium in genetic-association analyses via ridge regression. Am J Hum Genet 2008; 82: 375–385.
Tibshirani R : Regression shrinkage and selection via the lasso. J Roy Statist Soc Ser B (Methodological) 1996; 58: 267–288.
Lunn DJ, Whittaker JC, Best N : A Bayesian toolkit for genetic association studies. Genet Epidemiol 2006; 30: 231–247.
Conti DV, Witte JS : Hierarchical modeling of linkage disequilibrium: genetic structure and spatial relations. Am J Hum Genet 2003; 72: 351–363.
Kwee LC, Liu D, Lin X et al: A powerful and flexible multilocus association test for quantitative traits. Am J Hum Genet 2008; 82: 386–397.
Liu D, Lin X, Ghosh D : Semiparametric regression of multidimensional genetic pathway data: least-squares kernel machines and linear mixed models. Biometrics 2007; 63: 1079–1088.
Manly BFJ : Randomization, Bootstrap and Monte Carlo Methods in Biology, 3rd edn. FL Chapman & Hall: Boca Raton, 2006.
Elbers CC, van Eijk KR, Franke L et al: Using genome-wide pathway analysis to unravel the etiology of complex diseases. Genet Epidemiol 2009; 33: 419–431.
Fridley BL, Jenkins GD, Biernacka JM : Self-contained gene-set analysis of expression data: an evaluation of existing and novel methods. PLoS One 2010; 5: e12693.
Price AL, Zaitlen NA, Reich D et al: New approaches to population stratification in genome-wide association studies. Nat Rev 2010; 11: 459–463.
Clayton DG, Walker NM, Smyth DJ et al: Population structure, differential bias and genomic control in a large-scale, case-control association study. Nat Genet 2005; 37: 1243–1246.
Herold C, Steffens M, Brockschmidt FF et al: INTERSNP: genome-wide interaction analysis guided by a priori information. Bioinformatics 2009; 25: 3275–3281.
Zamar D, Tripp B, Ellis G et al: Path: a tool to facilitate pathway-based genetic association analysis. Bioinformatics 2009; 25: 2444–2446.
Luo L, Peng G, Zhu Y et al: Genome-wide gene and pathway analysis. Eur J Hum Genet 2010; 18: 1045–1053.
Chen L, Zhang L, Zhao Y et al: Prioritizing risk pathways: a novel association approach to searching for disease pathways fusing SNPs and pathways. Bioinformatics 2009; 25: 237–242.
Chen X, Wang L, Hu B et al: Pathway-based analysis for genome-wide association studies using supervised principal components. Genet Epidemiol 2010; 34: 716–724.
Nam D, Kim J, Kim SY et al: GSA-SNP: a general approach for gene set analysis of polymorphisms. Nucleic Acids Res 2010; 38: W749–W754.
Holden M, Deng S, Wojnowski L et al: GSEA-SNP: applying gene set enrichment analysis to SNP data from genome-wide association studies. Bioinformatics 2008; 24: 2784–2785.
Zhang K, Cui S, Chang S et al: i-GSEA4GWAS: a web server for identification of pathways/gene sets associated with traits by applying an improved gene set enrichment analysis to genome-wide association study. Nucleic Acids Res 2010; 38: W90–W95.
Acknowledgements
This research was supported by the Minnesota Partnership for Biotechnology and Medical Genomics grant, NCI grant CA136393 (Mayo Clinic SPORE in Ovarian Cancer), NCI grant CA140879, and NIAAA grant R03 AA019570. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflicts of interest.
Rights and permissions
About this article
Cite this article
Fridley, B., Biernacka, J. Gene set analysis of SNP data: benefits, challenges, and future directions. Eur J Hum Genet 19, 837–843 (2011). https://doi.org/10.1038/ejhg.2011.57
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/ejhg.2011.57
Keywords
This article is cited by
-
Working memory dysfunction in fibromyalgia is associated with genotypes of the catechol- O-methyltransferase gene: an event-related potential study
European Archives of Psychiatry and Clinical Neuroscience (2023)
-
Genomic architecture of phenotypic extremes in a wild cervid
BMC Genomics (2022)
-
Model-based clustering for identifying disease-associated SNPs in case-control genome-wide association studies
Scientific Reports (2019)
-
Methods and results from the genome-wide association group at GAW20
BMC Genetics (2018)
-
Variance explained by whole genome sequence variants in coding and regulatory genome annotations for six dairy traits
BMC Genomics (2018)