Introduction

With the availability of high-density maps of single-nucleotide polymorphisms (SNPs), association studies have become popular tools for identifying genes underlying complex human traits and diseases. For most current population-based genome-wide association studies (GWAS), statistical power is often limited because of the complex interplay among factors that influence the etiology of diseases.1 Increasing sample size and multilocus or multivariate statistical analyses can improve the power for detecting association. Sample size is often restricted because of genotyping costs and limited sample resources. Several studies have demonstrated that analyzing samples selected with extreme values can be more powerful than analyzing samples randomly selected from the population.2, 3, 4 In addition to using selected samples, another approach to increasing association test power is to perform joint analysis of multiple correlated phenotypes. For many common multifactorial traits, several correlated phenotypes are usually recorded for each individual during sample collection, but most often, the phenotypes are analyzed separately in a univariate framework. Joint analysis of correlated phenotypes can theoretically provide greater power than that provided by analysis of individual phenotypes.3, 5, 6, 7 Multivariate analysis can also alleviate the multiple testing problem, caused by testing different traits separately, and thereby improve the ability to detect genetic variants whose effects are too small to be detected in univariate analysis.8 Several multivariate approaches have been applied to linkage studies of correlated complex phenotypes, such as osteoporosis and bone-related phenotypes.9, 10, 11, 12 Similarly, various methods, often based on generalized estimating equations (GEEs), have been proposed for performing multivariate association tests on population- or family-based data.13, 14, 15, 16, 17, 18, 19, 20 Of the two studies that have investigated the power of bivariate association test in population-based data, one applied the restricted bivariate association test that assumes same quantitative trait locus (QTL) effects on each trait.16, 18 Such constraints in the model may have overestimated or underestimated the relative performance of bivariate over univariate analysis. Finally, GWAS studies using multivariate analysis are rare, especially in samples of subjects selected through their phenotype values, and further investigations using this approach are warranted.4

To this aim, we evaluated the statistical properties of joint association analysis of two correlated quantitative traits in samples of unrelated subjects through simulation studies using the seemingly unrelated regression (SUR) bivariate model that allows for different QTL effects on traits. The evaluation was conducted under different situations according to the sample selection design, genetic effects and residual correlation between the traits. We demonstrate the efficacy of SUR-based bivariate test by applying it to simultaneous GWAS analysis of two correlated bone phenotypes, bone mineral density (BMD) at the lumbar spine(LS) and at the femoral neck (FN), which are major risk factors of osteoporosis.

Materials and methods

SUR-based bivariate model

The SUR model21 is a generalization of a classical linear regression model that consists of several regression equations with potentially different sets of explanatory variables. It thus allows for a differential effect of explanatory variables on phenotypes as well as the possibility that some variables might be associated with only one trait. Let N be the total number of unrelated subjects (i=1, …, N), each having observations on two phenotypes yji (j=1, 2). Consider a system of two equations, where the jth equation is of the form: yj=Xj × βj+ej; yj is a N × 1 vector of the phenotypic values, Xj is a (Kj+1) × N matrix of explanatory variables with Kj representing the number of explanatory variables in the model for phenotype j excluding the intercept; is the (Kj+1) × 1 vector of coefficients and ej is a N × 1 vector of the residuals errors. The system of SUR can be written as:

The SUR model allows for cross-equation correlation of the residual terms. The covariance matrix of all the residuals is assumed to be normally distributed with mean 0 and covariance matrix where IN is a N × N unit matrix and Σ a 2 × 2 matrix with the following form:

σ12 and σ22 are the residual variances of Y1 and Y2, respectively, and rE is the residual correlation between Y1 and Y2.

The SUR model is estimated using the generalized least square method where the covariance matrix Ω is first estimated using ordinary least square regression in system (1). Linear restrictions on coefficients can be tested by an F test. The F statistic for systems of equations is: where, C is the matrix of restrictions on coefficients. Under the null hypothesis, the F statistic has a central Fisher distribution with 2 and 2 × N−K degrees of freedom, where K is the total number of estimated coefficients (K=K1+K2+2). The goodness of fit of the whole system can be measured by the McElroy's r-square (R2). R2 is the proportion of covariance because of X taking into account the residual matrix covariance Ω.22

Here, we applied the SUR model to test association between two continuous phenotypes in unrelated subjects genotyped at one SNP marker, and Xj is the N × 1 vector of genotypes at the SNP. Under an additive model, the genotype for each individual i, noted gi, is coded as a function of the number of minor alleles, that is, 0, 1 or 2. We computed the SUR model free of constraints on the regression coefficients, that is, β1 and β2 were freely estimated. Under the null hypothesis of no association to either one or both phenotypes, the F statistic has a central Fisher distribution with 2 and 2 × (N−2) degrees of freedom. Separate association analyses of Y1 and Y2 can be conducted using traditional univariate linear regression model: yj=g × βj+ej, where yj, g and βj are as described above but now, ej is assumed to follow a normal distribution N (0, σj2). The null hypothesis of no association (βj=0) can be tested against the alternative (βj≠0) with a Student's statistic (t-test) with N−2 degrees of freedom.

Simulation study

We considered genetic models of complex traits and specifically tried to generate correlated data, mimicking as much as possible our real BMD GWAS data (see below). As a strong (∼0.5) and positive phenotypic covariation exists for BMD values at the LS and at the FN,23 we generated data for two positively correlated quantitative phenotypes. Further, in real data sets, as causal loci usually contribute a small proportion to the total phenotypic correlation, residual correlation approximates phenotypic correlation between traits. It is also more realistic to assume that the investigator has a priori knowledge on the magnitude and sign of the covariation of the studied phenotypes than on the magnitude and sign of the QTL effect on each phenotype. Therefore, in all our scenarios, the sign of the residual correlation (rE) was positive, but the sign of the induced QTL correlation (rG) was either positive or negative. Also, our BMD GWAS study used a sampling design, with extreme truncate selection of unrelated males, aiming to improve power. Therefore, we also generated samples of subjects drawn from the extremes of the phenotype(s) population distribution.

The main scenarios and parameter settings are shown in Table 1. The different settings allowed us to generate data for a QTL having same or different effect on the two positively correlated phenotypes, and the two sources of covariation (QTL and residual) have same or opposite sign. Briefly, we assumed a biallelic QTL having additive effects (aj) on Yj (j=1, 2), with minor and major allele frequency q and p, respectively. The QTL contribution to Yj is the trait-specific QTL heritability, hj2. Here, we focussed our power investigation to QTLs explaining a relatively small part of the trait variance, that is, from 0.5 to 3% that, for complex traits, seemed to us more realistic. The genotypic means (mjk) of Yj are equal to 2q × aj, (q−p) × aj and −2p × aj when k, the number of minor alleles, is equal to 0, 1 and 2, respectively, and with . We varied the sign of aj: both were of same or opposite sign and the QTL correlation (rG) was, thus, equal to +1 or −1, respectively. We first generated samples of subjects unselected for their traits values (denoted as Su). Second, we generated subjects selected from the 2.5% (ie, trait value ≤−2) and 30% (ie, trait value >0.5) left and right tail of the population distribution of Y1 (denoted as S1), respectively. Third, we included Y2 in the selection design, that is, we selected subjects from the 2.5 and 30% left and right tail of the population distribution of Y1 and Y2, respectively, (denoted as S2). These truncate selection criteria (trait value ≤−2 or >0.5) are the values that we have used in our real BMD GWAS. Under S1 and S2, we generated samples with equal number of subjects drawn from the left (N/2) and the right (N/2) side of the phenotypes distributions.

Table 1 Outline of the main scenarios and varying parameter values in the bivariate data simulations
Full size table

Traits values of N (300, 1000)-unrelated subjects were generated as follows. For a given combination of parameter values (rE, h21, h22, rG), we first draw QTL alleles from a binomial distribution with parameter q, and built genotypes under Hardy–Weinberg equilibrium. Then, conditionally on the generated genotype, gk (k=0, 1, 2), we jointly drew the values of Y1 and Y2 via a bivariate normal distribution with mean (m1k, m2k)t and variance matrix Ω, given in equation (2). Third, under sampling S1 or S2, we applied the corresponding truncate selection, that is, individuals not fulfilling the selection criteria were withdrawn from the sample. Steps 1–3 were repeated until reaching the required left and right truncated sample sizes of (N/2) subjects.

Each replicate was analyzed with SUR-based bivariate and with two separate univariate analyses using the systemfit package of R software (http://www.r-project.org/) using the genotypes at the QTL, that is, the SNP is the causal variant. The mean and standard deviations of each association statistic (F test and t1, t2-tests) were derived from K replicates. Power and type I error rates of each association test were calculated as the proportion of replicates with a test statistic exceeding a given theoretical threshold (Rα) value, at nominal significance levels, α=5, 1, 0.1 and 10−3%. Type 1 errors were estimated in the settings were h21=h22=0 with K=20 000 replicates. Power rates were derived with K=1000 replicates. To compare the performance of bivariate and that of univariate association analysis, we computed the proportion of replicates where t1 and t2 were both lower than Rα. One minus this proportion estimated the probability to detect association to either one of the two phenotypes. To adjust for the two univariate association tests, we applied the Bonferroni correction, that is, we used the theoretical thresholds Rα/2.

Results

Simulation study

Tables 2 and 3 present the mean (and SD) association statistic of the SUR-based bivariate (F test) and of the traditional univariate tests (t-test), respectively, when N=1000 for 66 scenarios under the alternative hypothesis and when q=0.4. For a given QTL heritability value, the results did not vary, as expected, with q.

Table 2 Mean and SD (μF (SD)) of the SUR-based bivariate association statistic (F test) in samples of N=1000 subjects for various parameter settings: QTL heritability (h21/h22), sign of the induced genetic correlation (rG), residual correlation (rE) and sampling selection design
Full size table
Table 3 Mean and SD (μt (SD)) of the traditional univariate association statistic (t-test) in samples of N=1000 subjects for various parameter settings: QTL heritability (h21/h22), sign of the induced genetic correlation (rG), residual correlation (rE) and sampling selection design
Full size table

Bivariate association statistics

In randomly selected samples, the results in Table 2 show several well-established power figures. First, mean F statistics of bivariate association analysis increase with the size of the trait-specific QTL heritability (h21 and/or h22) irrespective of rG and rE. Second, the power is highest in presence (rG≠0) than in absence (rG=0) of pleitropic effects: the highest power is achieved when rG=−1, that is, when the correlation induced by the QTL effect and the residual correlation are opposite in sign. Third, the results also confirm that the power of bivariate association test varies with the size of the residual correlation: when rG=0 or rG=−1, the power increases with rE; conversely, when rG=+1, it decreases with rE. These general trends are observed irrespective of the sampling selection designs. Applying extreme truncate selection increases the power of bivariate association analysis, but the optimal selection design depends on the true genetic model. When rG=0 or rG=−1, extreme selection on one trait (S1) is more efficient than extreme selection on both traits (S2). Conversely, when rG=+1, S2 is more efficient than S1. Overall, under Su or S1, the highest mean F statistics are obtained when rG=−1, irrespective of rE. Under S2, the highest power is achieved when rG=+1 or when rG=−1, depending on the size of rE. Interestingly, when the traits are moderately (rE=0.20) correlated, mean F statistics have greater values when rG=+1 than when rG=−1.

Univariate association statistics

Table 3 shows again several well-established power figures. In randomly selected samples, the power of univariate analysis increases with the QTL heritability (h21/h22) and varies little with the size of the residual correlation, rE. For phenotype Y1, under a given QTL heritability (h21) value, the mean statistic values of all models are similar in the randomly selected samples. Applying extreme truncate selection increases the power of univariate association analysis of Y1. Under S1, the power remains similar whatever may be the rG value. Under S2, the power is the highest and the lowest for the pleiotropic models rG=+1 and rG=−1, respectively. When rG=−1 or rG=0, the power of univariate association analysis is greater under S1 than under S2. The reverse trend is obtained when rG=+1. For phenotype Y2, the power of univariate analysis depends on rG and rE. Further, applying extreme selection does not always lead to a gain in power. Indeed, when rG=−1, the power of univariate analysis is the greatest in the unselected samples (Su). When rG=0, the mean t-statistic values in the selected samples are biased and inflated. The magnitude of the bias is greater under S2 than under S1. Under S1, the bias increases with rE.

Overall, applying selection criteria on one or both traits is an optimal sampling design when rG=+1: the power of each separate univariate analysis is improved over that in randomly selected samples. When rG=−1, applying extreme truncate selection leads to both a substantial gain and decrease in power for Y1 and Y2, respectively. For the situations in which the QTL does not exert pleiotropic effects (rG=0), the highest power of univariate analysis of Y1 is obtained in the selected samples. However, the mean t-statistic values for Y2, the trait not associated to the QTL, are also increased. Type I error rates of separate univariate analyses may thus be inflated, especially in selected samples and when the residual correlation is high.

Type I error rates

When the QTL/SNP has no effect on Y1 and Y2, the values of the mean and standard deviation of both bivariate and univariate association tests are close to the theoretical values, regardless of the residual correlation, minor allele frequency of the studied SNP and of the selection sampling design (Supplementary Table 1A). Indeed, SUR-based bivariate and each separate univariate association tests have correct type I error rates (Supplementary Table 1B). However, the false positive rates of univariate association analyses for detecting association to either or both the two traits are, as expected, inflated: the estimated rates are roughly two times higher than the theoretical rates. Applying a Bonferroni correction (denoted as U_b) leads to slightly conservative significance levels, especially when the residual correlation between the traits is strong.

Power comparisons

The power to detect association to either or both of the two traits using SUR-based bivariate analysis was compared with the power of separate univariate analysis of Y1 and Y2 adjusted for multiple testing by the Bonferroni correction (denoted as U_b). Figure 1a shows the power curves (at significance of 10−5) against the QTL heritability (h21, h22) when N=1000 for moderately (rE=0.2) or strongly (rE=0.6) correlated traits. Power curves under S1 and S2 are shown in Figure 1b, when h21=h22=0.005, N=1000 and rE=0.2 or 0.6.

Figure 1
figure 1

Power rates at α=10−5 of SUR-based bivariate analysis and univariate analysis, adjusted for multiple testing by Bonferroni correction (U_b), in samples of N=1000 subjects and under various parameters settings: QTL heritability (h12/h22), sign of the induced genetic correlation (rG) and residual correlation (rE). (a) Power estimates against QTL heritability for moderately (rE=0.2) or strongly (rE=0.6) correlated traits in randomly selected samples (Su). (b) Power estimates under extreme selection (S1 or S2) for moderately (rE=0.2) or strongly (rE=0.6) correlated traits and QTL heritability (h12=h22=0.005).

Full size image

In randomly selected samples (Figure 1a), the relative advantage of SUR-based bivariate over univariate association analysis is more obvious not only when rG=−1 and/or the traits are strongly correlated (rE=0.6) but also when rG=+1 and the traits are moderately correlated (rE=0.2). Under S1 (Figure 1b), SUR-based bivariate is slightly less powerful than univariate analysis when rG=+1 and rE=0.6 or when rG=0 and rE=0.2. For strongly correlated traits, the power rates are equal to 94.5% (SUR) versus 29.3% (U_b) when rG=−1; 44.0% (SUR) versus 32.3% (U_b) when rG=0; and 36.8% (SUR) versus 39.9% (U_b) when rG=+1. For moderately correlated traits, the power rates are equal to 64.6% (SUR) versus 31.7% (U_b) when rG=−1; 32.9% (SUR) versus 34.9% (U_b) when rG=0; and 43.7% (SUR) versus 32.6% (U_b) when rG=+1. Under S2 (Figure 1b), SUR-based bivariate shows same or slightly lower power than univariate analysis, except when rG=−1 or when rG=0 and rE=0.6 where it outperforms univariate test. As already noted above, selecting on Y1 (S1) is the most efficient sampling design when rG=−1 or when rG=0 and the traits are strongly correlated (rE=0.6). Selecting on both traits (S2) is the most efficient design when rG=+1. Overall, when rE=0.6, the power of SUR is the greatest (94.5%) when rG=−1 and under S1, whereas the power of univariate analysis is the greatest (56.8%) when rG=+1 and under S2. When rE=0.2, the power of SUR and univariate analysis are both the greatest (72.5 and 72.9%) when rG=+1 and under S2. As shown in Supplementary Table 2, all these trends are confirmed under various parameter settings.

Analyses of empirical BMD genome-wide association data

BMD GWAS data

Subjects were recruited from the Network in Europe on Male Osteoporosis Study.24, 25 Subjects selected from this cohort were unrelated males >18 and <68 years of age. In addition, the subjects were selected by bone densitometry (measured at the LS and FN) criteria, having either low BMD (LS Z-scores ≤−2, n=175) or high BMD (both LS and FN Z-scores >0.50, n=155). Further details of the study sample are provided in Supplementary Table 3. Genotyping was carried out at the Centre National de Génotypage (Evry, France) using the Illumina 370K platform (Illumina, San Diego, CA, USA). SNPs and DNA data were subjected to standard quality control analyses with PLINK26 (details are provided in Supplementary Methods).

Association analysis

Our primary analysis was the joint association analysis of LS Z-scores and FN Z-scores by means of SUR-based bivariate test. For comparison purpose, we also applied separate univariate association analyses of LS and FN Z-scores. We used single-marker analysis assuming additive genetic effects. The mean F statistic of our SUR-based genome-wide association (GWA) analysis was equal to 1.018 (SD=1.022, median=0.70). The mean t-statistic of LS and FN were −0.0167 (SD=1.011, median=−0.0165) and −0.0129 (SD=1.006, median=0.0104), respectively. These results indicated that there was no meaningful inflation of univariate as well as bivariate association analyses.

Results

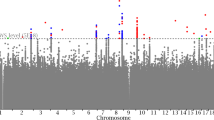
SUR-based bivariate analyses identified a substantial number (35) of SNPs with strong evidence of association (P-value <10−4). Interestingly, several of the identified SNPs failed to reach nominal (P-value <5%) significance under separate univariate analyses for either one or the two BMD phenotypes. Genome-wide bivariate and univariate association results were compared in terms of statistical significance and ranks of the SNPs identified in either one of the two approaches. For each SNP, we kept the lowest P-value (denoted as Best_U) of LS or FN univariate association analysis. Univariate P-values were not corrected for multiple testing. We ranked the Best_U P-values from the lowest to the highest. We similarly ranked the P-values from SUR-based bivariate analysis of LS and FN. Figure 2 plots the significance levels in each procedure for the top 100 most associated SNPs identified from SUR-based (Figure 2a) or from univariate (Figure 2b) analyses. We found that a majority (52) of the top SNPs in SUR-based bivariate analysis also show strong (P<3 × 10−4) association signal in univariate analyses. For a substantial number (16) of the remaining SNPs, univariate analyses fail to reach nominal (P<5%) significance (Figure 2a) On the other hand, all of the top 100 SNPs in univariate analyses (Figure 2b) are also highly significant (P<8 × 10−4) in bivariate analysis. Table 4 shows details of the association results for the top 10 SNPs in SUR-based and in each separate univariate analysis. The table also shows P-values and ranks found in each of the two other procedures. The genetic contributions (R2 values) of the 10 top SNPs are not great, as expected for any relatively common polymorphic locus. In all, 3 of the top 10 SNPs from bivariate analysis also rank well (ie, are in the set of top 300 SNPs) in univariate analyses of LS and/or FN. They are located on 6q25: rank=2, P=1.3 × 10−5 (LS) and rank=1, P=1.2 × 10−5 (FN); on 15q14-q15: rank=2635, P=8.4 × 10−3 (LS) and rank=3, P=1.7 × 10−5 (FN); and on 22q13: rank=1, P=3.5 × 10−6 (LS) and rank=8, P=3 × 10−5 (FN). All the remaining seven SNPs show a much stronger association signal in bivariate than in univariate analyses, including two of the three best SUR-based association signals. For the most significant result, on 22q11.2 (P=5.44 × 10−6), the QTL explains 3.85% of the joint (co)variance of LS and FN. This value likely overestimates the contribution in unselected populations. Nonetheless, univariate analyses failed to detect association (P>0.07) with this SNP. Conversely, all the top 20 SNPs identified from univariate analysis of either LS or FN belong to the set of top 42 SNPs from SUR-based bivariate analysis. Overall, our analyses showed that univariate analysis did not identify new strongly associated SNPs as compared with those detected in bivariate analysis. Conversely, SUR-based analysis identified strongly associated SNPs that were not detected in univariate analysis.

Figure 2
figure 2

Overlap in significance of results from bivariate and univariate (Best_U) association analysis. (a) Top 100 hits in SUR-based bivariate association test: −log10 P-values of univariate analysis against −log10 P-values of SUR-based bivariate analysis. (b) Top 100 hits in univariate association test: −log10 P-values of SUR-based bivariate analysis against −log10 P-values of univariate analysis.

Full size image
Table 4 Association results: top 10 most associated SNPs from SUR-based bivariate or from separate univariate analysis of LS and FN BMD
Full size table

Our study used a design, with extreme truncate selection of unrelated males, aiming to improve power. The approach of studying samples drawn from the extremes of the population distribution of BMD has been used in several linkage studies of BMD variation,25, 27 but rarely in association studies,28 and to our knowledge, never in samples drawn from the population of males. Owing to our relatively small GWA sample size, no SNP showed evidence of association to either one or both BMD phenotypes at genome-wide significance threshold of 1.7 × 10−7 (0.05/298 783 SNPs). However, we used an extreme truncate selection design that, as shown by our simulation studies, has increased power over unselected samples. Our SUR-based bivariate association analyses identified strong association (P<8.4 × 10−6) with three genomic regions (6q22.1, 15q14 and 22q11). These SNPs have not yet been reported to be associated with bone density in previous GWAS.29, 30, 31 Two of them, on 15q14-15 and 22q11, are located in genes that are known to be expressed in skeletal muscle:32, 33 GLUT 11 encoded by SLC2A11 on 22q11 and RYR3 on 15q14-15. Because muscle contraction has a major impact on bone density, this might represent an indirect role of these genes on bone density. These genetic variants, whether they are site specific or possibly shared (pleiotropic), may warrant further follow-up genetic studies on BMD and other bone-related phenotypes.

Discussion

We have evaluated the performance of bivariate association analysis based on the SUR model, which allows different genetic models for different traits. To our knowledge, this is the first study to specifically derive the power and the relative performance of bivariate association analysis in selected samples of unrelated subjects. Our main results coincide with well-known power figures,6, 7, 8 and confirmed that bivariate association analysis outperforms univariate analysis when the QTL exerts pleiotropic effects and the relative increase in power is the greatest when correlation of the QTL is opposite in sign to the residual correlation. The most powerful sampling selection design varied with the genetic model, specifically with the size and the direction of the induced QTL correlation. Applying truncate selection on one trait was found the most efficient sampling design when the genetic and the residual correlations are opposite in signs. The same most efficient design was found when the QTL does not exert pleiotropic effects: the power of the SUR-based bivariate association test was found as good as or better than that of univariate association test, depending on the size of the residual correlation. Finally, when the QTL exerts pleiotropic effects and both sources (QTL and residual) of covariation are of the same sign, applying selection criteria on both traits was found to be the optimal sampling selection design. Under this sampling design, the performance of SUR-based bivariate test relatively to univariate analysis decreases with the size of the residual correlation.

So far, two studies have investigated the power of bivariate association in unselected population-based data, and they both applied bivariate association test based on GEEs.16, 18 The former applied a general GEE-based model that allows, as the SUR model, for different QTL effects on the two traits. The second study used a GEE-based bivariate model that assumed same QTL effects on the phenotypes. Our results are congruent with those reported by the first study. The restricted bivariate test estimates, as the univariate test, a single parameter (ie, the SNP regression coefficients on each trait are all set as equal). Under the restricted bivariate model, the gain in power of bivariate analysis is enhanced and reduced when the QTL has similar effect and when it affects one trait only, respectively. Clearly, rarely, knowledge of this magnitude about a complex trait is known a priori. Thus, we do not recommend using restricted bivariate models even in unselected data.

Our bivariate GWA analysis of LS and FN BMD values, conducted in a sample of unrelated males with low BMD (LS Z-scores ≤−2) and high BMD (LS and FN Z-scores >0.5), consistently demonstrated the advantage of the SUR-based bivariate test over separate univariate analysis. All the top hits in univariate analysis also showed strong evidence of association in bivariate analysis. Conversely, additional SNP associations were detected with the bivariate method that did not reach nominal significance in single-trait analyses: this was achieved without adjusting significance of univariate analyses for multiple testing.

In conclusion, our results showed that SUR-based models are useful to detect association for correlated phenotypes. However, our results also showed that similar power levels can be achieved whether the QTL exerts or not pleiotropic effects. Thus, disentangling pure pleiotropic from residual covariation remains a challenge even in bivariate association analysis.