- NEWS AND VIEWS
- Correction 18 October 2021
Superconductivity in a graphene system survives a strong magnetic field
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Rent or buy this article
Prices vary by article type
from$1.95
to$39.95
Prices may be subject to local taxes which are calculated during checkout
Nature 595, 495-496 (2021)
doi: https://doi.org/10.1038/d41586-021-01890-3
Updates & Corrections
-
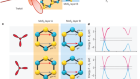
Correction 18 October 2021: In an earlier version of this article, the magic-angle twisted trilayer graphene shown in Figure 1 was incorrect. This has now been corrected.
References
Cao, Y., Park, J. M., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Nature 595, 526–531 (2021).
Read, N. & Green, D. Phys. Rev. B 61, 10267 (2000).
Kitaev, A. Y. Ann. Phys. 303, 2–30 (2003).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Sarma, S. D. Rev. Mod. Phys. 80, 1083–1159 (2008).
Cao, Y. et al. Nature 556, 43–50 (2018).
Cao, Y. et al. Nature 556, 80–84 (2018).
Park, J. M., Cao, Y., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Nature 590, 249–255 (2021).
Hao, Z. et al. Science 371, 1133–1138 (2021).
Lévy, F., Sheikin, I., Grenier, B. & Huxley, A. D. Science 309, 1343–1346 (2005).
Ran, S. et al. Nature Phys. 15, 1250–1254 (2019).
Leggett, A. J. Rev. Mod. Phys. 47, 331–414 (1975).
Competing Interests
The author declares no competing interests.

 Read the paper: Pauli-limit violation and re-entrant superconductivity in moiré graphene
Read the paper: Pauli-limit violation and re-entrant superconductivity in moiré graphene
 Heating freezes electrons in twisted bilayer graphene
Heating freezes electrons in twisted bilayer graphene
 Spectroscopy of graphene with a magic twist
Spectroscopy of graphene with a magic twist