- NEWS AND VIEWS
Helium nucleus measured with record precision
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Rent or buy this article
Prices vary by article type
from$1.95
to$39.95
Prices may be subject to local taxes which are calculated during checkout
Nature 589, 518-519 (2021)
doi: https://doi.org/10.1038/d41586-021-00120-0
References
Sick, I. J. Phys. Chem. Ref. Data 44, 031213 (2015).
Pohl, R. et al. Nature 466, 213–216 (2010).
Pohl, R., Gilman, R., Miller, G. A. & Pachucki, K. Annu. Rev. Nucl. Part. Sci. 63, 175–204 (2013).
Krauth, J. J. et al. Nature 589, 527–531 (2021).
Pohl, R. et al. Science 353, 669–673 (2016).
Sick, I. Phys. Rev. C 77, 041302 (2008).
Yerokhin, V. A., Patkóš, V. & Pachucki, K. Phys. Rev. A 98, 032503 (2018).
König, K. et al. Rev. Sci. Instrum. 91, 081301 (2020).

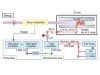 Read the paper: Measuring the α-particle charge radius with muonic helium-4 ions
Read the paper: Measuring the α-particle charge radius with muonic helium-4 ions
 Progress on the proton-radius puzzle
Progress on the proton-radius puzzle
 Exotic helium atom lit up
Exotic helium atom lit up




