- NEWS
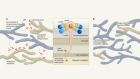
The mathematical strategy that could transform coronavirus testing
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Rent or buy this article
Prices vary by article type
from$1.95
to$39.95
Prices may be subject to local taxes which are calculated during checkout
Nature 583, 504-505 (2020)
doi: https://doi.org/10.1038/d41586-020-02053-6
References
Mutesa, L. et al. Preprint at https://arxiv.org/abs/2004.14934 (2020).

 Coronavirus and COVID-19: Keep up to date
Coronavirus and COVID-19: Keep up to date