- NEWS AND VIEWS
Atomic forces mapped out by lasers
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Rent or buy this article
Prices vary by article type
from$1.95
to$39.95
Prices may be subject to local taxes which are calculated during checkout
Nature 583, 35-36 (2020)
doi: https://doi.org/10.1038/d41586-020-01913-5
References
Lakhotia, H. et al. Nature 583, 55–59 (2020).
Morales, F., Richter, M., Patchkovskii, S. & Smirnova, O. Proc. Natl Acad. Sci. USA 108, 16906–16911 (2011).
Ghimire, S. & Reis, D. A. Nature Phys. 15, 10–16 (2019).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. Nature 518, 179–186 (2015).
Tancogne-Dejean, N., Sentef, M. A. & Rubio, A. Phys. Rev. Lett. 121, 097402 (2018).
Silva, R. E. F., Blinov, I. V., Rubtsov, A. N., Smirnova, O. & Ivanov, M. Nature Photon. 12, 266–270 (2018).
Murakami, Y., Eckstein, M. & Werner, P. Phys. Rev. Lett. 121, 057405 (2018).
von Hoegen, A., Mankowsky, R., Fechner, M., Först, M. & Cavalleri, A. Nature 555, 79–82 (2018).
Gerber, S. et al. Science 357, 71–75 (2017).

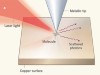
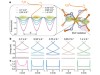 Raed the paper: Laser picoscopy of valence electrons in solids
Raed the paper: Laser picoscopy of valence electrons in solids
 Snapshots of vibrating molecules
Snapshots of vibrating molecules
 Holograms from electrons scattered by light
Holograms from electrons scattered by light





