- NEWS AND VIEWS
On-demand entanglement could lead to scalable quantum networks
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Rent or buy this article
Prices vary by article type
from$1.95
to$39.95
Prices may be subject to local taxes which are calculated during checkout
Nature 558, 192-193 (2018)
doi: https://doi.org/10.1038/d41586-018-05336-1
References
Kurpiers, P. et al. Nature 558, 264–267 (2018).
Humphreys, P. C. et al. Nature 558, 268–273 (2018).
Kimble, H. J. Nature 453, 1023–1030 (2008).
Cirac, J. I., Zoller, P., Kimble, H. J. & Mabuchi, H. Phys. Rev. Lett. 78, 3221–3224 (1997).
Axline, C. J. et al. Nature Phys. https://doi.org/10.1038/s41567-018-0115-y (2018).
Reiserer, A. & Rempe, G. Rev. Mod. Phys. 87, 1379–1418 (2015).
Hucul, D. et al. Nature Phys. 11, 37–42 (2015).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Nature 414, 413–418 (2001).
Chou, C.-W. et al. Science 316, 1316–1320 (2007).
Pfaff, W. et al. Science 345, 532–535 (2014).
Maring, N. et al. Nature 551, 485–488 (2017).
Andrews, R. W. et al. Nature Phys. 10, 321–326 (2014).

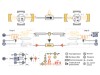 Read the paper: Deterministic quantum state transfer and remote entanglement using microwave photons
Read the paper: Deterministic quantum state transfer and remote entanglement using microwave photons
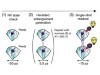 Read the paper: Deterministic delivery of remote entanglement on a quantum network
Read the paper: Deterministic delivery of remote entanglement on a quantum network
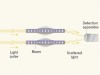 Entangled vibrations in mechanical oscillators
Entangled vibrations in mechanical oscillators
 Quantum signals could soon span the globe
Quantum signals could soon span the globe




