- NEWS AND VIEWS
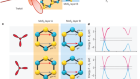
Solitons divide and conquer
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Rent or buy this article
Prices vary by article type
from$1.95
to$39.95
Prices may be subject to local taxes which are calculated during checkout
Nature 554, 179-180 (2018)
doi: https://doi.org/10.1038/d41586-018-01470-y
References
Kivshar, Y. S. & Agrawal, G. Optical Solitons: From Fibers to Photonic Crystals (Academic, 2003).
Lahav, O. et al. Phys. Rev. X 7, 041051 (2017).
Liu, X., Qian, J. & Wise, F. W. Phys. Rev. Lett. 82, 4631–4634 (1999).
Minardi, S. et al. Phys. Rev. Lett. 105, 263901 (2010).
Shih, M. et al. Opt. Lett. 21, 324–326 (1996).
Strecker, K. E., Partridge, G. B., Truscott, A. G. & Hulet, R. G. Nature 417, 150–153 (2002).
Ackerman, P. J. & Smalyukh, I. I. Nature Mater. 16, 426–432 (2017).
McLeod, R., Wagner, K. & Blair, S. Phys. Rev. A 52, 3254–3278 (1995).

 One ring to multiplex them all
One ring to multiplex them all
 Single electrons pop out of the Fermi sea
Single electrons pop out of the Fermi sea