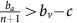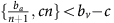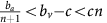Main

Tumours are highly heterogeneous ecosystems (Welch, 2016), with various cancerous and non-cancerous sub-populations of cells competing for access to space, growth-factors, nutrients, oxygen and other limited resources. This emergence and persistence of heterogeneity has implications for diagnosis, treatment and disease progression (Dexter and Leith, 1986; Maley et al, 2006; Venkatesan and Swanton, 2015). Current explanations of intra-tumour heterogeneity include evolutionary neutrality (Iwasa and Michor, 2011), niche specialisation (Nagy, 2004; Gatenby and Gillies, 2008), non-equilibrium dynamics (Gonzalez-Garcia et al, 2002) and frequency-dependent selection (Tomlinson, 1997; Tomlinson and Bodmer, 1997; Basanta et al, 2008). It remains an open problem to identify which, or how many, of these mechanisms are at work in any given neoplasm (Merlo et al, 2006).

The progression of neoplasms to metastatic disease is marked by the acquisition of a number of hallmarks (Hanahan and Weinberg, 2000; Hanahan and Weinberg, 2011), including self-sufficiency of growth factor production for angiogenesis and reprogramming energy metabolism for aerobic glycolysis. As with many of the other hallmarks, there is evidence of intra-tumour heterogeneity in both the production of cytokines like vascular endothelial growth factor (VEGF) (Achilles et al, 2001; Marusyk and Polyak, 2010) and glycolysis (Kallinowski et al, 1988; Willmann et al, 2015; Hensley et al, 2016). Given that it is possible for an individual cancer cell to not invest (as heavily) in angiogenesis or not forgo the benefit of oxygen by avoiding aerobic glycolysis then how do these population level traits evolve, and how are they maintained? We answer this question with a mathematical model that treats acid production through glycolysis as a tumour-wide public good that is coupled to the club good of oxygen from better vascularisation.

By investing in better vascularisation—by (over)-producing VEGF, for example—the whole tumour can benefit from an improvement in vascularisation and the subsequent rise in availability of nutrients and oxygen (Nishida et al, 2006). An individual cancer cell, however, could reap these benefits from mere proximity to (over)-producers and save on the energetic cost of producing the relevant growth-factor: free-riding on the benefits created by other cancer cells. These free-riding cancer cells could out-compete the (over)-producers and take over the tumour. Such a switch away from growth factor (over)-production, however, decreases the overall fitness of the tumour—hurting the society of cancer cells—by making fewer nutrients and less oxygen available to all cancer cells. What is favourable at the individual level is unfavourable at the tumour population level. This represents a classic example of an evolutionary social dilemma.

A similar social dilemma exists for the increase of acidification from glycolysis. It is striking that the upregulation of glycolysis—the so called Warburg effect (Warburg et al, 1926; Warburg, 1956a, 1956b)—is observed even in the absence of hypoxia (Pauwels et al, 2000; Gambhir, 2002; Hanahan and Weinberg, 2011). Glycolysis is comparatively inefficient in terms of ATP yield when oxygen is not a limiting factor, raising the conundrum of what selective advantage it provides to a cell to compensate for its energetic cost. The acid-mediated tumour invasion hypothesis suggests that this advantage comes from the acidification of the tumour micro-environment that leads to higher proliferation and invasiveness through increased extracelluar matrix degradation and an increase in normal cell death (Gatenby, 1995; Gatenby and Gawlinski, 1996; Gatenby and Gawlinski, 2003; Gatenby and Gillies, 2004). Tumour cells typically achieve a maximum proliferation rate with an extracellular pH that is acidic enough (pHe=6.8) to lead to normal cells’ death from activation of p53-dependent apoptosis pathways and loss of function of critical pH-sensitive genes (Rubin, 1971; Casciari et al, 1992; Park et al, 1999; Webb et al, 2011). Thus, acidosis provides a (relative) benefit to acid-resistant tumour cells competing against the acid-sensitive non-cancerous cells.

Early models have assumed that resistance to acidity is available only to glycolytic cells (Gatenby and Gawlinski, 1996; Basanta et al, 2008; Basanta et al, 2011), but there is little evidence to suggest that aerobic cancer cells could not also develop this resistance. In human colonic adenoma, for example, low extracellular pH is accompanied by p53-dependent apoptosis in wild type. But cells that lost wild-type p53—a common mutation among cancer cells—receive a selective growth advantage independent of their metabolic process (Williams et al, 1999). In fact, recent in silico models parameterised from experimental data suggest that tumours acquire glycolytic capacity after acid resistance (Robertson-Tessi et al, 2015). In the absence of hypoxia, resistant non-glycolytic cells could benefit from aerobic metabolism to out-compete the glycolytic cancer cells without contributing to acidosis. Such a switch away from glycolysis decreases the overall acid production by the tumour, normalising pH, and negating part of the advantage acid-resistant cells have against non-cancerous soma. This individual benefit hurts the society of cancer cells and qualifies acid production as another evolutionary social dilemma.

Evolutionary game theory (EGT) is a tool to make sense of these sort of social dilemmas. Originating with Maynard Smith and Price (1973), EGT is a mathematical approach to modelling frequency-dependent selection where players interact via phenotypic strategies. EGT has been used in oncology to study the conditions that select for more aggressive tumour phenotypes in gliomas (Basanta et al, 2008; Basanta et al, 2011), colorectal cancer (Gatenby and Vincent, 2003; Gatenby et al, 2005), multiple myeloma (Dingli et al, 2009) and prostate cancer (Basanta et al, 2012); as well as the effects of treatment on the progression of cancer (Basanta et al, 2012; Orlando et al, 2012).

Recently, Archetti introduced the public goods game to oncology for looking separately at two-strategy problems like growth-factor production (Archetti, 2013) and the production of acid in the Warburg effect (Archetti, 2014). With colleagues, he has implemented the growth-factor production game in an experimental system (Archetti et al, 2015). He concluded that a heterogeneous (polyclonal) equilibrium of producers and non-producers cannot exist unless the benefits that these goods provide are nonlinear in the number of producers. In the linear cases, considered separately, this would predict that VEGF (over)-producers (VOP) and glycolytic (GLY) cells would both go extinct, leaving a population of aerobic cells that do not call for more vasculature (DEF). This is in accord with the intuition that free-riders always win in social dilemmas, and would result in the elimination of heterogeneity of production of VEGF and acidity. However, angiogenesis and glycolysis are intimately related and should not be considered in isolation because the benefits of oxygen affect the degree of hypoxia and thus the relative cost of glycolysis when compared with aerobic metabolism.

We focus on this inter-dependence of these two hallmarks by coupling the two goods—the public good of acidification and the club good of vascularisation—in a three-strategy game. Our model reveals dynamics that cannot be predicted from treating micro-environmental acidification and vascularisation in isolation from each other. In particular, we show dynamic cycles of constantly changing proportions of cancer cell types—a realisation of intra-tumour heterogeneity even with linear goods. This has consequences for the design of treatments, as it suggests that the timing, and order, of therapeutic interventions could drastically affect the outcome. For example, it shows the importance of preparatory treatment or neoadjuvant therapy that manages the low-frequency cell types in contrast to simply targeting the most common clone, and of the advantages of targeting the tumour micro-environment instead of just targeting the cancer cell.

Materials and methods

Double goods game

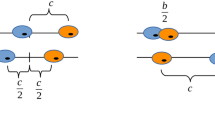
Consider a focal glycolytic cell interacting with n other nearby cells of which nG∈[0, n] are also glycolytic. Together they produce a relative benefit ba(nG+1) due to acidity to be distributed among the n+1 cells. Therefore, this focal glycolytic cells receives a net benefit of .

By averaging over all possible focal glycolytic cells and interaction group compositions, we get that the expected fitness of a population of glycolytic (GLY) cells with random assortment is

where xG is the proportion of GLY in the population, and the angle brackets represent averaging with, in this case, nG sampled from the binomial distribution with n trials and xG as the probability of success (i.e., choosing a GLY cell). It is possible to include an explicit cost of glycolysis in equation (1), but this is mathematically equivalent to adjustment to ba or (relative) fitness of the aerobic cells (for more detail, see Supplementary Appendix A.2).

For an aerobic cell—non-GLY—in a similar case, the benefit due to acid is only , since it does not itself produce acid. But, in addition to the effects of acid, an aerobic cell benefits from a more efficient metabolism by using the oxygen delivered by the vasculature. In particular, a VEGF (over)-producer (VOP) will receive the benefit but pay a cost c for the higher production, and the aerobic non-(over)-producer of VEGF (DEF) will receive the benefit but pay no cost, essentially free-riding.

Therefore, the expected fitness of the two aerobic populations with random assortment are

where xV, xD are the proportions of VOP and DEF in the population, and the averages in the second summands are taken with nG, nV sampled from the multinomial distribution with n trials and xG as the probability of the first outcome (i.e., choosing a GLY cell), and xV as the probability of the second outcome (i.e., choosing a VOP cell). In each equation, the first summand is the benefit due to acidification and the second is the benefit from the club good of vascularisation. These fitness functions are described in more detail in Supplementary Appendix A.

Note that, unlike acidity, the benefit of oxygen from vasculature is divided among only the n−nG+1 non-glycolytic cells in the interacting group and not all n+1 cells in the interaction group. Such a good that excludes some (GLY) but is distributed evenly among the others—regardless of if they contributed (VOP) or not (DEF)—is known in economics as a club good (Buchanan, 1965). Alternatively, for an ecological connection, we can think of glycolytic cells as loners in the optional public goods game (Hauert et al, 2002).

Evolutionary dynamics

The evolutionary dynamics of the population are given by the replicator equation (Taylor and Jonker, 1978; Hofbauer and Sigmund, 1998):

where is the average fitness of the population.

Alternatively, we can write down these dynamics in their factored form (see Supplementary Appendix B for a proof of equivalence) as:

where p=xG is the proportion of GLY, is the proportion of aerobic cells that (over)-produce VEFG, and is the average fitness of the aerobic cells.

These equations are accurate for large populations at carrying capacity—in vivo tumours up against a resource limitation or managed by an immune response—or in their exponential growth phase—typical of in vitro experiments. In other cases they serve as an approximation. See Supplementary Appendix C for more discussion on interpreting replicator dynamics.

Results

We can apply the double goods game described in the previous section to study the temporal evolution of different populations in various scenarios. These scenarios are set by the four micro-environmental parameters of our model: ba, the benefit per unit of acidification; bv, the benefit from oxygen per unit of vascularisation; c, the cost of (over)-producing VEGF; and, n, the number of interaction partners in the public good. Within a scenario, the last piece of information is the initial proportions of cells xG(0), xV(0), xD(0) (or p(0), q(0) in the factored form). The values of these variables will depend on the particular cancer ecosystem (i.e., patient and type of tumour). Since these variables can be difficult or impossible to measure clinically, it is important to understand what broad qualitative relationships between them mean for long-term dynamics.

Although the fitness functions in equations (1, 2, 3) are Bernstein polynomials of degree n, we can use properties of binomial coefficients to simplify the corresponding gain functions of the factored replicator dynamics without any approximation (see Supplementary Appendix D). This allows us to rewrite equations (7) and (8) as

Notice that when p=0, equation (9) recovers the social dilemma of angiogenesis that we discussed in the introduction with the free-riding DEF cells taking over the population of aerobic cells, driving q towards 0. When p≠0 and q=0, we have a hypoxic tumour, and glycolytic cells are favoured, driving p towards 1. On the other hand, if p≠0 and q=1, then we recover the social dilemma of aerobic glycolysis, with VOP cells favoured if ba<(bv−c)(n+1), and GLY cells otherwise. In other words, if one of the strategies is absent in the population then no persistence of heterogeneity is possible among the remaining two strategies. This is consistent with predictions from two-strategy linear public goods games.

The more interesting case that is unique to our model is when all three strategies are initially expressed in the population. In this setting, we can analytically characterise the population dynamics into one of three the qualitatively different regimes based on the values of the four main micro-environmental parameters by solving how the above gain functions for p and q cross zero (for more information, see Supplementary Appendix D). This classification is shown visually in Figure 1. We name these three regimes by their end points (and evolutionarily stable strategies); fully glycolytic (green region in Figure 1), fully angiogenic (red) and heterogeneous (yellow). The following three subsections describe each of these three regimes in turn. Example dynamics from each regime are given in the inset simplexes of Figure 1.

Figure 1
figure 1

The three possible dynamic regimes for the double goods game.The possible parameter settings for bv are varied horizontally, starting at c. The possible parameter settings for are varied vertically, starting at 0. Each of the three inset simplexes have the same coordinates, with the top vertex corresponding to all GLY, left to all VOP, and right to all DEF. Each simplex is a typical example of dynamics within its regime. The specific micro-environmental parameters for each example: (1) ba=37.5, bv=2, c=1, n=4 for green; (2) ba=2.5, bv=7, c=1, n=4 for red; and (3) ba=2.5, bv=2, c=1, n=4 for yellow.

Full size image

Fully glycolytic tumours: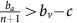

We solve for the average fitness of aerobic cells as

where the first summand is the benefit from acidification, and the second summand is the benefit due to oxygen from vascularisation. Since DEF only consume the club good from vascularisation, without producing any, equation (11) is maximised to bap+bv−c when all aerobic cells are producers of the club good (i.e., all VOP, q=1).

Similarly, we can solve for the fitness of GLY:

where the first summand is the benefit from acidosis that all cancer cells receive, and the second summand is the slight increase in acidification that glycolytic cells get from always being in a group with an extra acid producer (themselves).

From this, we see that if the fitness benefit of a single unit of acidification is higher than the maximum benefit from the club good for aerobic cells (bv−c), then the difference between equations (12) and (11) is always positive. Thus, GLY will always have a strictly higher fitness than aerobic cells, and be selected for. In this scenario, the population will converge towards all GLY, regardless of the initial proportions (as long as there is at least some GLY in the population). This dynamic regime is achieved for any micro-environmental parameter settings corresponding to the green region in Figure 1.

Fully angiogenic tumours: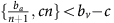

Consider an interaction group with nV VOP and nD DEF cells. If the focal agent interacting with this group is an (over)-producer, then it will receive a benefit from oxygen of . If the focal agent is a defector, then they will receive . Since, by definition, nV+nD is less than the interaction group size n, then regardless of the number of glycolytic cells:

Thus, if the benefit to (over)-producers from their extra unit of vascularisation is higher than the cost c to produce that unit (or, equivalently, if bv−c>cn) then VOP will always have a strictly higher fitness than DEF, selecting q towards 1. In addition, if the maximum possible benefit of the club good to aerobic cells (bv−c) is higher than the benefit of an extra unit of acidification then (based on the difference of equations (12) and (11), or the negation of the conditions in the previous section) for sufficiently high number of (over)-producers (q close enough to 1), GLY will have lower fitness than aerobic cells. When both conditions are satisfied, the population will converge towards all VOP. This dynamic regime is achieved for any micro-environmental parameter settings corresponding to the red region in Figure 1. Notice in the typical example dynamics inset Figure 1 that if a population starts with mostly aerobic cells (p close to 0) that are not overproducing VEGF (q close to 0), then the population might see a transient decrease in the number of aerobic cells on the way to the all-VOP equilibrium.

Heterogeneous tumours: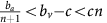

From equation (13), we know that if the benefit from an extra unit of vascularisation in a fully aerobic group is lower than the cost c to produce that unit, then for a sufficiently low proportion of GLY and thus sufficiently large number of aerobic cells sharing the club good, DEF will have higher fitness than VOP. This will lead to a decrease in the proportion q of (over)-producers among aerobic cells and thus a decrease in the average fitness of aerobic cells (see equation (11)). A lower fitness in aerobic cells will lead to an increase in the proportion of GLY until the aerobic groups (among which the club good is split) get sufficiently small and fitness starts to favour VOP over DEF, swinging the dynamics back. Thus, resulting in cyclic dynamics, examples of which can be seen in the top panel of Figure 2 or inset Figure 1.

Figure 2
figure 2

Dynamics for an untreated tumour and examples of two different sets of dynamics resulting from changed timings of a given intervention.Each graph is proportion of cells vs time, with GLY (xG) in green, VOP (xV) in solid red and DEF (xD) in blue. The dashed red lines show the proportion of VOP among aerobic cells . All three graphs start with same initial conditions (p(0)(=xG(0))=0.9, q(0)=0.6) and the same tumour micro-environment (ba=2.5, bv=2, c=1, n=4). In the top panel, we highlight the cyclic behaviour by noting when p and q return to their initial values given by the green circles and red hollow circles, respectively. In the second and third panel, we consider an anti-glycolytic treatment of the same strength (subtracting 3 from the fitness of GLY) and the same duration (three time steps). The difference between the second and third panel is in timing, marked in grey: the second panel starts treatment at t=0, and the third at t=10. If the proportion of a cell-type goes below 10−4 then it dies off entirely. At t=30, no cell types are extinct in the top panel; in the second and third panel, the only non-extinct cell types are GLY and DEF, respectively. This highlights the importance of the timing of therapy for evolutionary outcome.

Full size image

Under this scenario, the population will orbit around an internal fixed-point at and . The exact position of p* is the solution to the polynomial equation (see Supplementary Appendix D for details). The amplitude of the orbit will depend on the distance between p(0), q(0) and p*, q*. This dynamic regime is achieved for any micro-environmental parameter settings corresponding to the yellow region in Figure 1.

Therapeutic implications

With the possible dynamic regimes in mind, we can think about treatment in one of two ways: (1) treatments that target the player by directly reducing the proportion of a given strategy in the population; or (2) treatments that target the game by changing the parameters (ba, bv, c or n) and taking us from one dynamic regime to another. In both cases, we need to be mindful of counter-intuitive phenomena, such as timing and order effects and the importance of managing heterogeneity.

Treat the player: targeting cell types

A treatment that targets a given strategy and can be applied long enough to drive that strategy to extinction can be considered a viable intervention. If we were in the first dynamic regime (green in Figure 1; ) or the second dynamic regime (red in Figure 1; ), then the population will always converge towards all-GLY or all-VOP, respectively. This means that unless the strategy-targeting therapy is strong and long enough to drive that strategy to extinction, it will not affect the overall outcome beyond a potential transient delay. In particular, the timing of the therapy will not have a qualitatively significant effect. In the heterogeneous case (yellow in Figure 1; ); however, counter-intuitive results are possible and the timing of treatment becomes important.

As an example in Figure 2, we consider a tumour described by the micro-environmental parameters ba=2.5, bv=2, c=1 and n=4 and an initial composition xG=0.9, xV=0.06, xD=0.04. If left untreated then the proportions of strategies would cycle around an internal fixed point at , as seen in the top panel. In that panel, the proportion of glycolytic cells xG will oscillate between about 0.9 and 0.34 with a period of about 26 time units.

In the standard paradigm of personalised medicine, treatments target the most abundant subclone. In this case, it would be the glycolytic cells—the most common, and least fit, strategy at t=0. We can imagine targeting these cells specifically, with a therapy that imposes a large fitness cost, like lonidamine (Floridi et al, 1981), for example. Here, we choose to set the fitness cost of this therapy to 3, which leads to very quick and aggressive reduction in the GLY population. In a perfect world, the therapy would be applied long enough to drive GLY to extinction. But what happens if it is only applied for three time units, enough to drastically reduce the proportion of GLY cells—below detectable levels—but not below the extinction threshold? The cyclic dynamics then allow the glycolytic cells to recover by out-competing the mostly DEF population. To make matters worse, as GLY recovers, VOP is pushed below the extinction threshold leaving just the other two cell types to compete. Without VEGF (over)-production, the remaining aerobic cells are less fit than the glycolytic cells and are also driven to extinction. The overall result at t=30 is a relapse with even more glycolytic cells than before treatment. In this scenario, while the goal was to eliminate glycolytic cells, the opposite occurred: elimination of all the aerobic cells and creation of a completely glycolytic tumour.

If instead the treatment was delayed until t=10—when the GLY cells are at their lowest proportions, and highest fitness, in the tumour’s natural cycle—then much more favourable results could be achieved. With the lower initial proportion of GLY cells, three units of time are long enough to drive the cells to extinction. Without glycolytic cells, the competition between DEF and VOP becomes a classic social dilemma and the VEGF (over)-producers are driven to extinction. The result is now what was desired: an aerobic tumour with no—or significantly diminished—ability to recruit blood vessels.

In this case, we can think of the natural tumour dynamics as a neoadjuvant ‘treatment’ that lowered the GLY population slightly while preparing the VOP–DEF composition to be in a favourable position after therapy.

Treat the game: targeting micro-environment

Consider the hypothetical case-study in Figure 3. Here, we have a situation with poor vasculature (bv=2, c=1, n=4) and a highly glycolytic tumour (p0=0.9, ba=37.5). If left untreated, the tumour would quickly reach all-GLY, driving the other two strategies extinct. Thus, the primary goal is to eliminate GLY, and create an easier-to-target all-VOP tumour. The secondary goal is to do so with minimal transient tumour heterogeneity. We consider two possible interventions. The treatments can be applied sequentially with a window of one time-step between them or simultaneously. One treatment is a buffer therapy (Robey et al, 2009) that reduces the benefit of acidity; setting ba=2.5 from then on. Another is vascular normalisation therapy (VNT) (Jain, 2013); setting bv=7 from then on. In Figure 3, the top panel considers giving buffer therapy followed by VNT, the middle panel has the VNT preceding the buffer therapy and the bottom panel has both treatments at given simultaneously at t=0.

Figure 3
figure 3

Three possible orders of therapeutic intervention.Each graph on the left shows the proportion of cells vs time, with GLY (xG) in green, VOP (xV) in red and DEF (xD) in blue. The dashed red lines show the proportion of VOP among aerobic cells . Each graph on the right is ba/(n+1) vs bv and shows how treatment moves the tumour between qualitatively different dynamic regimes through the space on micro-environmental parameters (for detailed explanation see Figure 1). All graphs start with same initial proportions (xG(0)=0.9, q(0)=0.6). The untreated tumour has parameters ba=37.5, bv=2, c=1 and n=4. In the top two panels, two treatments are applied: the first at time 0 and the second at time 1. In the last panel, a single treatment is applied at time 0. We consider two game-targeting treatments: (1) a buffer therapy that reduces the benefit of acidity (setting ba=2.5 from then on; horizontal arrows in the right panel); and (2) a vascular normalisation therapy (VNT; setting bv=7 from then on; vertical arrows in the right panel). In the top panel, buffer therapy is followed by VNT, the second panel shows VNT followed by buffer therapy, and in the final panel both treatments are given simultaneously (diagonal arrow in the bottom right panel).

Full size image

The buffer then VNT (top panel) ordering produces immediate results, with the proportion of GLY no longer increasing—and even starting to decline—right away and reaching minimal levels earlier than VNT followed by buffer therapy (middle panel). However, the top ordering increases the heterogeneity among the anaerobic cells and although the tumour will eventually move to a state of all VOP, by time-step 3 (when it is nearly all VOP for the middle panel) there is a high level of VOP–DEF heterogeneity, and earlier during treatment (say t=2) the top panel has heterogeneity in all three cell types. Something that the physician wanted to avoid.

In contrast, the middle ordering sees no immediate results from the VNT. Instead, this first treatment can be thought of as a neoadjuvant therapy that eliminates the VOP–DEF heterogeneity among the rare aerobic cells before targeting the predominantly GLY population. By time-step 3, the middle ordering sees a similarly high level of response in the GLY phenotype, but without creating a high level of heterogeneity in the tumour.

We might expect that both normalising the benefit due to oxygen from vascularisation and decreasing the benefit from acidification at the same time would offer superior results to sequential therapy. However, as we can see from the bottom panel of Figure 3, this is not necessarily the case. Although the same reduction in glycolytic cells is reached 1 time unit faster than the sequential therapies, the heterogeneity among aerobic cells remains high; like buffer therapy followed by VNT.

Staggering buffer therapy after VNT might not produce immediately evident results but it lets us reach those results without encountering a highly heterogeneous tumour. When targeting the micro-environment, it matters which qualitatively different dynamic regimes the game goes through, even if the final micro-environmental parameters are the same.

Discussion

We introduce and classify the double goods game of acidity and vasculature. There are three qualitatively different dynamic regimes that end in a tumour that is either: (1) fully glycolytic (all-GLY); (2) fully angiogenic (all-VOP); or (3) a heterogeneous (polyclonal) cycle in proportions of all three cell types. Which of these regimes is achieved depends on the micro-environmental parameters like the benefit per producer due to acidity (ba), due to vasculature (bv) and the cost of (over)-producing VEGF (c). We show that polyclonal tumours made up of three different cellular strategies are evolutionarily stable even with linear goods. This stands in stark contrast to the all-DEF equilibrium that we would expect from considering the linear goods in isolation. Our results highlight the difficulty of ruling out possible dynamics from overly reductionist accounts of cancer, and the importance of modelling both the vascularisation and acidity when studying the Warburg effect (Warburg, 1956a, 1956b).

The dynamic nature of the polyclonal equilibrium reminds us of the importance of tracking the tumour composition through time, not basing treatment on measurements from a single time-point, and optimising the timing of treatment. As an example, we consider an anti-glycolysis treatment like lonidamine (Floridi et al, 1981). If timed correctly and applied for long enough, then this treatment can drive the glycolytic cells extinct and reduce the tumour to the two-strategy case of VEGF-production considered in prior work (Archetti, 2013). From there, somatic evolution will drive VEGF (over)-producers extinct, leaving us with an all- DEF tumour (lower panel of Figure 2). However, if the same treatment is applied at the wrong time in the cycle of heterogeneity (or not for long enough) then the glycolytic population can recover while the VEGF (over)-producers are driven extinct by non-producers. Without VEGF (over)-producers, the glycolytic cells can out-compete the aerobic cells and drive them to extinction, resulting in a fully glycolytic tumour (middle panel of Figure 2). A backfire effect for treatment.

Since the heterogeneous equilibrium is not the only possible outcome of these game dynamics, it is also important to measure the micro-environmental parameters such as the benefit per unit of vascularisation and per unit of acidification that determine the game. This dichotomy between tumour composition and micro-environmental parameters carries over from measurement to treatment. In section ‘Treat the game: targeting micro-environment’, we consider treatments like buffer therapy (Robey et al, 2009) and VNT (Jain, 2013) to change the micro-environmental parameters and thus target the game. By shifting to a more desirable game, we allow natural somatic evolution to lead us to a better outcome. The order in which we shift between games is important, especially for transient heterogeneity.

For highly glycolytic tumours, it is important to consider neoadjuvant VNT before buffer therapy. VNT allows us to reduce the heterogeneity in aerobic cells before targeting the more common glycolytic cells. Thus, when buffer therapy turns the game against glycolytic cells, the tumour is prepped in a low heterogeneity state and moves to an all-VOP phenotype without high levels of transient polyclonality. If buffer therapy is applied before VNT, or even if the two are applied simultaneously, then the response of glycolytic cells is not only quicker but also prone to creating much longer lasting heterogeneity in the tumour. We expect that similar considerations of neoadjuvant therapy for managing the rarer cancer sub-types might prove effective in other treatment settings.

There are several different types of heterogeneity that can work for or against the patient. These include strategy heterogeneity (i.e., a polyclonal tumour) and game heterogeneity (i.e., differences in micro-environmental parameters). Physicians have to be mindful of both types when treating a given patient. So far, we concentrated on difference in micro-environmental parameters due to variation between patients, tissues and the effects of therapy. However, there can also be game heterogeneity within different regions of the same tumour. For example, Kaznatcheev (2015) have previously shown that the game within the bulk of the tumour can differ from the game at static boundaries. But it is through static boundaries like blood vessels, organ capsules or basement membranes that metastatic invasion happens. Theoretical future work could more explicitly model invasiveness by coupling our double goods game to the go-vs-grow game (Basanta et al, 2008) and also broadening the analysis to ex situ cells. If physicians want to minimise the risk of metastates then it is important to measure the micro-environmental parameters at such boundaries.

To make our EGT empirical, we need to concentrate on building experiments that apply recently developed protocols for measurements of microscopic games (Gore et al, 2009; Archetti et al, 2015; Li et al, 2015) to classic model systems of acid production and oxygen consumption (Rubin, 1971; Casciari et al, 1992; Park et al, 1999; Williams et al, 1999). Although the linear goods we consider in this paper are useful for defining protocols and approximating initial measurements, in future it would be helpful to fully analyse the nonlinear double goods game that we define in Supplementary Appendix A. This can be done by either adapting general tools such as the (Pena et al, 2014) analysis of sign changes of gain sequences, or by considering specific extreme cases like step functions. However, it is only through experimental work that we can determine the kinds of games that cancer cells play, and thus which modelling extensions are most fruitful to pursue.