Introduction

DNA has been proven to be a highly powerful material for molecular computing and an excellent engineering material for biochemical circuits because of properties such as commercial synthesis at a relatively low cost, self-assembly into defined structures, special recognition of target sequences and so on.1, 2, 3, 4, 5, 6, 7, 8, 9 Up to now, all common logic operations, including AND, OR, INHIBIT, IMPLICATION, XOR and so on, have been mimicked with DNA as a template.10, 11, 12, 13, 14, 15 It is important to develop higher-level logic circuits for data processing and the fabrication of nanodevices, which usually require combinatorial logic gates.16, 17 For example, a half adder can perform an addition operation on two binary digits by integration of an XOR gate and an AND gate in parallel to generate a SUM (S) output and a CARRY (C) output, respectively. As a key building block, the half adder is used to construct more advanced computational circuits and is in high demand in information technology.18 A half subtractor can perform a subtraction of two bits, which requires the combination of an XOR gate and an INHIBIT gate to produce a DIFFERENCE (D) output and a BORROW (B) output, respectively. Despite their fundamental and practical importance, investigations of molecular half adders and half subtractors are at an early stage.19, 20, 21, 22, 23 Meanwhile, only a small portion of the available reports is DNA related. It is worthwhile to note that the reported DNA-based half adders or half subtractors suffer from two main limitations. One is that the required two logic gates are developed separately and realized with different platforms.24, 25, 26, 27 Recently, DNAzyme-based half adder and half subtractor were achieved by mixing all the necessary DNAzyme subunits in a single test tube. The inputs hybridize with different DNAzyme subunits selectively to construct the required logic gates.18 The other limitation is that the inputs for the required two logic gates are different from each other.26 The above investigations serve as promising proofs of principle for the construction of advanced molecular logic circuits. From the point of view of potential applications, the required two logic gates for a half adder or a half subtractor should be implemented with a universal platform stimulated by the same set of inputs.27 To fulfill the requirements of increased computational complexity, it is important to construct multicomponent devices on a single biomolecular platform.17 Keeping that in mind, a simple and universal DNA-based platform is developed for the first time to implement the required two logic gates of a half-adder arithmetic processing triggered by the same two inputs. By simply modifying the inputs, a half subtractor is achieved with the same platform as that used for the half adder.

Experimental procedure

To meet the requirements of the developed half adder and half subtractor, the DNA sequences used in the experiments were first designed and then mimicked in the website http://mfold.rna.albany.edu/?q=DINAMelt/Two-state-melting. According to the mimic results, experiments were performed to find whether the designed DNA sequences were available for the half-adder and half-subtractor arithmetic processings. According to the experimental results, the DNA sequences were redesigned. The above procedures were repeated until available DNA sequences were obtained.

The synthesized oligonucleotides were purchased from Shanghai Sangon Biotechnology (Shanghai, China). N-methylmesoporphyrin IX (NMM) was purchased from Porphyrin Products (Logan, UT, USA). All the other chemicals were purchased from Aladin (Shanghai, China) and used as received without further purification. The DNAs were dissolved in Tris-HCl (20 mM, pH 8.0) buffer solution containing KCl (50 mM) and MgCl2 (10 mM), and quantified by measuring the UV-visible absorption at 260 nm. The DNA solutions were heated at 90 °C for 10 min and then gradually cooled to 35 °C to mix the required inputs and then cooled to room temperature. The platform of the designed system was prepared by simply mixing A-DNA (25 nM) and B-DNA (50 nM). Here the concentration of A-DNA was first fixed. The concentration of B-DNA was found by gradually increasing the B-DNA content in the A-DNA solution until the fluorescent intensity of the system remained constant (see Supplementary Figure S5). The concentrations of the inputs were found by gradually increasing the input into the AB-DNA solution until the fluorescent intensity of the system recovered to a constant value. The inputs (100 nM) were added into the platform according to the logic operations. Here, input 1 (IN1) was used as a model molecule to perform the dynamic experiment to measure the time-dependent fluorescence change of the AB-DNA system (see Supplementary Figure S1). The concentration of NMM was 1 μM. The fluorescence spectra were recorded at room temperature by irradiating 6-carboxyfluorescein (FAM) at 492 nm and NMM at 399 nm.

Results and discussion

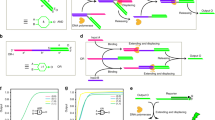
The half adder is designed according to the hybridization and displacement of DNA strands, as well as the formation and dissociation of a G-quadruplex (G-4), as shown in Figure 1. All the DNA sequences can be found in Supplementary Table S1. A half adder requires two distinct output signals, which are generated by the fluorescent dyes FAM (emission max at 521 nm) and NMM (emission max at 609 nm) in the developed system. As shown in Figure 1, the mixture of NMM and the partially hybridized duplex AB-DNA is used as the platform for the arithmetic processing. The 3′-terminus of the A-DNA is labeled with FAM as a fluorophore and the 5′-terminus of the B-DNA is labeled with DABCYL as a quencher. The fluorescence of FAM is quenched or recovered, depending on the distance from the quencher to the fluorophore, which is controlled by various inputs. The fluorophore NMM acts as another signal indicator for the designed half adder. NMM is a commercially available anionic porphyrin, characterized by a pronounced structural selectivity for G-4 and not for duplexes, triplexes or the single-stranded form.28 The fluorescence of NMM will be significantly enhanced on binding to G-4 and forming an NMM/G-4 complex,29 whose formation depends on the various inputs in the developed system. To perform the half-adder function, the inputs are designed to include the two segments shown in Figure 1 and Supplementary Table S1. The segments (I) of the two inputs are designed to hybridize with the AB-DNA platform to cause an output change of FAM. The segments (II) of the two inputs are related to the formation of the G-4 complex and thus modulate the output signal of NMM.

Figure 1
figure 1

Implementation principles of the developed DNA-based half adder and half subtractor, and the corresponding circuits.

Full size image

Here we first discuss the XOR logic operation of the half adder with FAM as a fluorescent indicator. As shown in Figure 1, the hybridization of AB-DNA holds the fluorophore and the quencher in close proximity, leading to a weak fluorescent signal due to the static quenching (Figure 2a). When IN1 is added, the A-DNA is released from the AB-DNA duplex, as B-DNA exhibits a more favorable hybridization with IN1 than with A-DNA, thus forming an IN1/B-DNA duplex. The replacement of the DNA separates the fluorophore from the quencher, restoring the fluorescent signal (Figure 2b). Dynamic experiments have been performed and the results are shown in Supplementary Figure S1. Similarly, the B-DNA is released from the AB-DNA duplex in the presence of input 2 (IN2), because A-DNA prefers to hybridize with IN2 over B-DNA, thus forming an IN2/A-DNA duplex. The fluorophore thus becomes far away from the quencher and exhibits a restored fluorescent signal (Figure 2c). When both inputs coexist, the duplex of IN1/IN2 is formed, as the hybridization of IN1 and IN2 is favored over hybridization with either B-DNA or A-DNA. Neither the A-DNA nor the B-DNA of AB-DNA is replaced by the IN1 or the IN2. Therefore, the fluorophore and the quencher still stay together in the AB-DNA duplex, yielding a low output signal of FAM (Figure 2d). The hybridization activation of the DNAs is validated by measuring the thermal stabilities of the formed duplexes (see Supplementary Figure S2). According to the fluorescent outputs of FAM, the characteristic XOR logic gate is achieved when the output is read at 521 nm. Here, the presence of each input is defined as ‘1,’ and the absence of the respective input is considered as ‘0.’ The output signal is defined as ‘1’ or ‘0’ when the normalized fluorescent intensity is higher or lower than 0.5, respectively. The definitions are available for the following logic operations. Figure 3 shows the normalized fluorescent intensities of the system at 521 nm as a function of the various inputs. The system exhibits ‘1’ in the presence of the individual inputs; otherwise, it remains ‘0’. The XOR logic operation performs the SUM digit function in the half adder as shown in the Truth Table 1.

Figure 2
figure 2

The fluorescent responses of FAM and NMM as output signals for the half adder corresponding to the various inputs: in the absence of the two inputs (a and e), in the presence of IN1 (b and f) and IN2 (c and g), and in the presence of the two inputs (d and h).

Full size image
Figure 3
figure 3

The normalized fluorescent intensities of the system at 521 (green column for the XOR logic gate) and 609 nm (red column for the AND logic gate) as a function of the various inputs (IN1 and IN2).

Full size image
Table 1 Truth table of a half adder
Full size table

Accompanying the XOR logic operation, the AND logic operation of the half adder is realized in the designed system with NMM as the output signal. In the absence of the two inputs, a low NMM fluorescent signal is detected (Figure 2e). As shown in Figure 1, the segment (II) of IN1 contains three guanine bases at the 5′-terminus and the segment (II) of IN2 contains a G-rich sequence (5′-GGGGTTTTGGGTTTTGGG-3′) at the 3′-terminus. Both segments (II) are designed to be uninvolved in the replacement reactions of the DNA as discussed in the above XOR logic gate. When either input is added individually, no G-4 is formed in both cases (see Supplementary Figure S3),14 producing a low fluorescent signal (Figures 2f and g). When the two inputs are added simultaneously, a duplex of IN1/IN2 is formed, associating the G-rich sequences of the two inputs together to create G-4.14 The NMM is then bonded to the resultant G-4, yielding an enhanced fluorescent signal (Figure 2h). The normalized fluorescent intensities of the system at 609 nm as a function of the inputs are plotted in Figure 3 (red column). It is clear that the system exhibits ‘1’ only when both inputs coexist, which is the feature of an AND logic gate. The AND logic gate is responsible for the CARRY digit function in the half adder, as shown in Truth Table 1. On the basis of the above Results and Discussion, the AND and the XOR gates are implemented in parallel with a universal platform and are triggered by the same set of inputs, fitting the requirements for a half adder.27

Inspired by the results, a half subtractor was constructed based on the same platform by simply modifying the inputs as shown in Figure 1. A half subtractor requires the parallel implementation of an XOR gate and an INHIBIT gate to code for the DIFFERENCE and BORROW digits, respectively. Noting that an XOR logic gate is needed in a half subtractor just as in a half adder, the segments (I) of the half-subtractor inputs share the same sequences as those in segments (I) of the half-adder inputs, responding to the hybridization and replacement of the DNA. To implement an INHIBIT logic function, the segment (II) of IN1 used in the half adder is redesigned as an oligonucleotide sequence containing 17 cytosine and adenine bases as shown in Figure 1. The redesigned input for the half subtractor is named INA. The segment (II) at the 3′-terminus of IN2 used in the half adder is redesigned as an oligonucleotide sequence containing 24 guanine and thymine bases, named as INB for the half subtractor, shown in Figure 1 and Supplementary Table S1. Here, the 24 guanine and thymine bases oligonucleotide can form G-4 to combine with NMM, producing a strong fluorescent signal from the NMM/G-4 complex (see Supplementary Figure S4), which has been confirmed in a previous report.29 The 17 cytosine and adenine bases of INA is partly complementary with the 24 guanine and thymine bases of INB, leading to a higher hybridization stability of the INA/INB duplex compared with the IN1/IN2 duplex. The resulting INA/INB duplex blocks the formation of the INB/G-4 complex, leading to a weak NMM fluorescent signal (see Supplementary Figure S4).

Triggered by the redesigned inputs, a half subtractor is implemented using the same platform as in the half adder. As the segments (I) of INA and INB are the same as those of IN1 and IN2, the XOR logic gate of the half subtractor with FAM fluorescence as the output signal can still be realized according to the above discussions for the XOR gate of the half adder. Similar fluorescence responses of FAM (Figure 4) are observed as those in the half-adder operation (Figure 2). The system yields lower output signal intensities at 521 nm in the absence or the simultaneous presence of both inputs and produces higher output signals in the presence of each individual input, which is clearly shown in Figure 5 (green column). Different from the half-adder processing, the XOR logic gate codes for a DIFFERENCE digit in the half-subtractor arithmetic processing shown in Truth Table 2. Meanwhile, an INHIBIT logic operation is implemented with NMM as another signal indicator. In the presence of INA, no G-4 is formed and a low NMM fluorescence output is observed (Figure 4f). In the presence of INB, complex NMM/G-4 is formed at the terminus of the A-DNA/INB duplex, producing a significant fluorescence output signal (Figure 4g). When the two inputs coexist, the INA and INB hybridize together, inhibiting the formation of the G-4 and leading to a low fluorescence output of NMM (Figure 4h), similar to the fluorescent response of NMM when both the inputs are absent (Figure 4e). The standard fluorescent intensities at 609 nm as a function of the various inputs are plotted in Figure 5 (red column). As a result, an INHIBIT logic gate is achieved when the output is read at 609 nm, implementing the BORROW digit function in the half subtractor, as shown in Truth Table 2. According to the above Results and Discussion, a half subtractor is successfully achieved by constructing XOR and INHIBIT logic gates in parallel with a universal platform that is stimulated by the same set of inputs.

Figure 4
figure 4

The fluorescent responses of FAM and NMM as output signals for the half subtractor corresponding to the various inputs: in the absence of the two inputs (a and e), in the presence of INA (b and f) and INB (c and g), and in the presence of the two inputs (d and h).

Full size image
Figure 5
figure 5

The normalized fluorescent intensities of the system at 521 (green column for the XOR logic gate) and 609 nm (red column for the INHIBIT logic gate) as a function of the various inputs (INA and INB).

Full size image
Table 2 Truth table of a half subtractor
Full size table

Conclusion

In summary, a half adder and a half subtractor are successfully demonstrated in a proof-of-principle by combining the hybridization and replacement of DNA strands. Specifically, introducing a G-4 into a half-adder or a half-subtractor system to modulate the output signal makes it flexible, enabling the design of various logic gates according to the requirements of the data processing. The demonstrated system presents great potential advantages for the development of DNA-based logic circuits. The required two logic gates of the developed half adder (or half subtractor) are implemented with a universal DNA-based platform and triggered by the same set of inputs. The developed system overcomes the limitations of the required two logic gates being achieved with different platforms or being triggered with different inputs. This is also the first report that implements a half adder and a half subtractor that share the same DNA platform. The use of the formation of a G-4 as the signal mediation element makes it flexible for the design of various logic gates according to the arithmetic processing requirements. Moreover, a constant threshold value is available for all the developed logic gates. The developed systems in our investigations fulfill the requirements for potential applications of a half adder and a half subtractor. It should be noted that there is a long road ahead to integrate the developed molecular systems to compete with silicon-based technology. Although the developed half adder and half subtractor are implemented in an experimental stage, these investigations provide a novel prototype for the design and assembly of higher-order circuits for arithmetic operations on the molecular level and develop a new method for constructing multicomponent devices on a single biomolecular platform.