Abstract
The discovery of bulk metallic glasses (BMGs) has stimulated widespread research enthusiasm because of their technological promise for practical applications and scientific importance in understanding glass formation and glass phenomena. Arising from their disordered atomic structure and unique glass-to-supercooled liquid transition, BMGs represent a new class of structural and functional materials with extraordinary properties including extreme strength at low temperature and high flexibility at high temperature, along with a number of superior chemical and physical properties. This article covers the general properties of BMGs based on a review of the historical milestones in metallic glass research, and recent progress on several fundamental issues in the development of a comprehensive understanding of the strength, ductility and glass-forming ability of BMGs and, more importantly, the correlation of these parameters with atomic structure, focusing on the outstanding questions and critical issues that appear to warrant future research. Recent advances in the applications of BMGs in microelectromechanical systems (MEMS), biomedicine and nanotechnology are also reviewed.
Similar content being viewed by others
Main
Bulk metallic glasses, formed at very low critical cooling rates, are fundamentally different from traditional amorphous alloys, which are usually formed at very high cooling rates in order to suppress the nucleation of crystalline phases. The high cooling rates required for the formation of traditional glassy alloys restrict the range of possible structures that can be prepared to powders, films and ribbons. Of the extensive family of glasses, BMGs are probably the youngest, possessing a number of characteristics, such as amorphicity and high strength, that are shared by other glasses, including the most familiar window (oxide) glasses. However, the most important feature of BMGs that, along with other glasses, distinguish them from general amorphous materials is the glass transition that transforms supercooled liquids into a glassy state when cooled from high to low temperature and vice versa. Metallic glasses are therefore scientifically defined as amorphous alloys that exhibit a glass transition, from which derives their unique properties of extreme strength at low temperature and high flexibility at high temperature, along with thermodynamic and physical properties that change abruptly at the glass transition temperature (Tg).
Research on metallic glasses is closely related to that on metallic liquids. It is known that the atomic configurations of molten metals and alloys are disordered. The noncrystalline structure is expected to be retained if the liquids can be quenched at a sufficiently high cooling rate to suppress the formation of equilibrium crystalline phases. The critical cooling rate required to freeze the liquid structure is estimated to be on the order of 105–106 K s−1 for alloys. This assumption was proved experimentally in 1959 by a research group at Caltech, who reported the first glassy alloy with a composition of Au75Si25 produced by splat quenching 1. In this pioneering work, the Au75Si25 melt was quenched using a cold metal plate instead of the water or oil used traditionally. The good contact between liquid droplets and the cold metal avoids the formation of gaseous layers that limit the heat release during solidification. Moreover, the droplets spread into a thin layer for rapid thermal diffusion when striking the solid, cold metal plate. X-ray diffraction analysis revealed the disappearance of all crystalline structure and the formation of a noncrystalline structure in the resultant micrometer-sized flakes. Following this discovery, a large number of metallic glasses were found in various alloy systems, and rapid research progress was made in the search for new metallic glasses. This research was accelerated by the invention of a melt spinning method,2 a rapid cooling technique that can routinely quench liquid alloys as 10–50 μm thick ribbons at cooling rates of 103–106 K s−1 by impinging a melt stream on a spinning copper wheel. Most glass-form alloys reported at that time were binary alloys, and their glass-forming ability was found to be strongly reliant on alloy composition. Good glass formers usually have compositions close to the eutectic points that correspond to a reaction from one liquid phase to two solid phases concurrently in the equilibrium binary phase diagram.3 In practice, limiting the search for new alloys to phase regions close to deep eutectic points is a shortcut for finding good glass formers in binary and ternary alloy systems. In principle, this supports the view that metallic glasses are frozen metallic liquids because an alloy with a eutectic composition generally has a low melting temperature and a stable liquid phase.
The requirement for high cooling rates in the formation of metallic glasses restricts the range of forms that can be produced in glassy alloy systems to small particles or thin ribbons. However, a few exceptions were found in noble metal based alloys, such as Pd-Cu-Si and Pd-Ni-P.3,4,5,6 These alloys have very low critical cooling rates of ∼10 K s−1 and can make glassy samples with a bulk size of ∼10 mm in thickness.5 Unfortunately, these pioneering works on the development of BMGs did not make a big impact in the materials science community. One reason is that, although the noble metals of palladium and platinum are good for improving glass-forming ability, they are too expensive to be used for a wide range of applications. The breakthrough in BMG research came with the discovery of multicomponent glass formers by Inoue and co-workers at Tohoku University.8,9 These new bulk glassy alloys exhibit excellent glass-forming ability and very low critical cooling rates for bulk glass formation, similar to those of the noble metal-based metallic glasses (Figure 1).7,9 Significantly, noble metals were no longer the essential constituent elements in these new alloys. Some excellent glass formers contain only transition metals, such as the system of Zr-Al-Ni-Cu. Soon after these findings, Peker and Johnson at Caltech reported an excellent multicomponent BMG with a composition of Zr41.2Ti13.8Cu12.5Ni10.0Be22.5 10. It is worth noting that this alloy contains 22.5 at% beryllium, the smallest metallic atom, which is expected to fill empty space in the defective glass structure and more efficiently stabilize the liquid and glass phases. To date, this alloy is still one of the best glass formers and probably best illustrates the effect of a multicomponent composition in ensuring the densest packing in zirconium-based BMGs. Encouraged by these successes, other excellent bulk glass formers were soon found in the iron-, nickel-, titanium-, and copper-based alloy systems,9 and it became possible to investigate the mechanical, physical and chemical properties of metallic glasses systematically. The bulk sizes also hold great promise for a wide range of structural and functional applications. These research achievements have opened a new field of BMGs and stimulated enthusiasm for metallic glass research. The ability to form BMGs very easily from common elements has naturally aroused much interest and led to rapid development in this field.7
Representative morphology, microstructure and thermal properties of bulk metallic glasses. (a) Bulk metallic glass prepared by mold casting. The fully amorphous sample has a diameter of ∼30 mm. (b) Typical high-resolution electron microscopy image and electron diffraction pattern (inset) of a BMG (adapted from Ref. 54, © 2006 APS). The maze-like disordered structure persists down to the sub-nanoscale. (c) Differential scanning calorimetry curve for a bulk glassy sample, showing the glass transition and wide supercooled region (courtesy of W. Zhang, Tohoku University, Japan).
Mechanisms of BMG formation
As aforementioned, deep eutectic points in binary and ternary alloy systems have been widely used as an indication for seeking good glass formers. However, it is impossible to represent more than three components on a phase diagram, and the eutectic transitions in quaternary and higher systems are rarely known. Therefore, it is difficult to locate the compositions for best glass formers in multicomponent alloy systems. Most multicomponent metallic glasses found so far have been identified by trial and error, and the development of new BMGs requires considerable experience and involves major commitments in time and resources. There is thus a compelling demand for research that uncovers the underlying mechanisms for the formation of BMGs.
Empirical rules
Following the discovery of multicomponent bulk glass formers, there have been many discussions on the underlying mechanisms of BMG formation. The excellent glass-forming ability of the new alloys has been generally attributed to the increased atomic packing density in the multicomponent system, as there are more atoms of the ‘right’ size to fill free space in the randomly packed glass structure. This appears to be true since the total energy of alloys with directionless metallic bonding depends on the packing density; denser packing leads to lower energy and thereby higher stability. Besides consideration of the packing density, the improved glass-forming ability of the multicomponent systems has also been nominally understood by the ‘confusion principle’, i.e., the more elements involved, the lower the chance that the alloy can select viable crystal structures, and hence the greater the chance of glass formation.11
Since the discovery of metallic glasses by Duwez in 1959, a number of empirical rules on metallic glass formation have been suggested in consideration of factors such as atomic size, interatomic bonding, electron density and other structural features.12 Although these empirical rules work for certain alloys, they frequently fail for others. By statistically analyzing hundreds of alloys that have excellent glass-forming ability, Inoue suggested a more comprehensive set of empirical rules for the formation of BMGs:9 alloys should be multicomponent systems consisting of more than three elements, there should be a significant difference in the atomic size ratios (>12%) among the three main constituent elements, and the three main constituent elements should have negative heats of mixing. Although most of the best glass formers follow those empirical rules, implying certain physical principles indeed play vital roles in the formation of BMGs in multicomponent systems, the empirical rules represent only the bare essentials for glass formation and are not sufficient for designing new alloys. The definite physical mechanisms for BMG formation therefore remain unclear, and the laws for quantitative composition design of bulk metallic glasses are still unknown.
Structural origins of metallic glass formation
As the key to glass formation is avoiding the occurrence of detectable crystals during cooling from liquid to a temperature below the glass transition point, the kinetics of crystal formation in supercooled liquids has been considered as the controlling factor for glass formation. According to the homogeneous crystal nucleation theory, crystal nucleation rates depend strongly on the diffusivity of alloy melts, which is a function of viscosity from the Stokes–Einstein equation. Therefore, dense liquids with high viscosity are expected to have a more stable liquid state and better glass-forming ability. Several atomic motifs, such as face-centered cubic (fcc) and hexagonal close-packed (hcp) and icosahedral structures, are known to yield the densest atomic packing. As fcc and hcp are the basic structure units of a large number of crystals, such atomic configurations in supercooled liquids have the potential to directly become the embryos of crystalline phases, and thus fail to explain the excellent stability of metallic glasses in the supercooled state. Local icosahedral order has been suggested as the most promising atomic motif of stable supercooled liquids and BMGs because the icosahedra are highly close-packed, lack translational periodicity, and are difficult to grow compared with their crystalline counterparts.13 From a topological point of view, atomic packing efficiency is closely related to the atomic size ratio between the solute and solvent atoms, and a ratio close to 0.902 can produce the most efficient atomic packing with icosahedra-like clusters as the predominant short-range order. The atomic size ratio of constituent elements has therefore been proposed as an important factor governing glass-forming ability, particularly in binary alloys that only contain transition metals.14 Recently, effective atomic size ratios have been used to evaluate the packing efficiency of multicomponent BMGs based on the average atomic size of the solvent weighted by the nominal alloy composition.15,16,17,18 However, the optimal composition for the best glass formers cannot be determined from the ideal effective atomic size ratio of ∼0.902 because of the multiple compositional variables of the multicomponent alloys and the possible chemical heterogeneity of the constituent elements.
One important clue for understanding the underlying mechanism of BMG formation is that the best formers of BMGs generally have a narrow compositional range.9 Changing the composition even slightly or replacing the constituent elements can lead to a dramatic loss of glass-forming ability. This characteristic is very similar to certain crystalline and quasicrystalline compounds with complex atomic configurations, such as Laves phases and icosahedral phases. Therefore, the exact composition requirements for the best glass formers indicate an inherent correlation between glass-forming ability and atomic structure in BMGs. Understanding the atomic structure of the best glass formers is probably a viable route to the goal of quantitatively designing new BMGs with ultra-high glass forming ability and excellent physical, chemical and mechanical properties.
The widely accepted structural model for metallic glasses is Bernal’s dense random packing model, in which metallic glasses are regarded as frozen metallic liquids with an atomic arrangement determined by purely geometrical sphere packing.19,20 Bernal’s idea can satisfactorily model the systems of monatomic metals and alloys with constituent species having comparable atomic sizes. However, it does not provide structural models for the short- and medium-range order observed in real, multicomponent glassy systems with very low critical cooling rates. Moreover, it has been found that this model fails to describe metal–metalloid-based alloys with pronounced chemical short-range order. In light of this, Gaskell proposed a stereochemically defined model that stipulates that the local unit of nearest neighbors in amorphous metal–metalloid alloys should have the same type of structure as the corresponding crystalline compounds with a similar composition.21,22,23 However, this model has not been found to be supported in metal–metal based metallic glasses. Even for metal–metalloid-based BMGs, the model is insufficient to explain the excellent stability of the supercooled liquid state. Regardless of the atomic configurations, it has been generally accepted that the disorder of metallic glass can only be preserved down to a certain length scale. Atoms in metallic glasses prefer to form short-range order in which the local nearest-neighbor environment of each atom is similar to other equivalent atoms, but this regularity does not persist over an appreciable distance. Due to the fact that good glass formers have a higher density than ordinary amorphous alloys with high critical cooling rates, it has been suggested that high packing density is essential to achieve high glass forming ability.8,10,24 Therefore, densely packed icosahedral clusters have been widely considered as a possible structural unit of BMGs. A number of simulations and experimental observations have suggested that icosahedra are an energetically favorable atomic structure in metal–metal-based metallic glasses.25,26,27,28,29,30 However, the metallic glasses that can form icosahedral quasicrystals during annealing in supercooled liquid regions generally have a marginal glass-forming composition and are not the best glass formers 25. This fact indicates that densely packed icosahedra may not be the only essential structure unit in metallic glasses.
A recent extended X-ray absorption fine structure (EXAFS) study showed that the excellent glass-forming ability of the multicomponent alloy Cu45Zr45Ag10 is associated with atomic-scale structural/chemical heterogeneity by the formation of zirconium-rich interpenetrating clusters centered on silver atom pairs and strings as well as copper-centered icosahedral polyhedra enriched with copper. Therefore, the atomic configurations of multicomponent BMGs appear to be rather diverse due to variations in the interatomic interactions of the constituent elements 18. Structural/chemical heterogeneity may be a universal phenomenon in multicomponent BMGs, as has been demonstrated by the recent observations of structure and property variations at different length scales in many metallic glass systems.31,32,33,34
In practical materials, the densely packed atomic structure of metallic glasses must be extended to the macroscopic scale. Current knowledge of short-range order is insufficient to determine the overall structure of a disordered solid, which is dramatically different from a crystal, for which it is only necessary to solve the structure for a subunit that can be repeated periodically to produce the whole structure. Defining the structure of metallic glasses beyond the nearest-neighbor short-range order has remained an outstanding issue in metallic glass research. Recently, Miracle suggested a scheme for modeling medium-range order in multicomponent metallic glasses.15 In his model, efficiently packed solute-centered atomic clusters are retained as local structural units. An extended structure is produced by idealizing these clusters as spheres and efficiently packing these sphere-like clusters in fcc and hcp configurations to fill three-dimensional space (Figure 2). Because of internal strains and topological frustration, the order of the cluster-forming solutes cannot extend beyond a few cluster diameters, and thus the disordered nature of metallic glasses can be retained beyond the nanoscale. Based on experimental measurements and computational simulations, Sheng and co-workers proposed an alternative cluster packing scheme to resolve the atomic-level structure of amorphous alloys. By analyzing a range of model binary alloys involving different chemistries and atomic size ratios, they elucidated the different types of short-range order as well as the structure of medium-range order. Their results suggest that icosahedral fivefold packing is a more favorable ordering pattern for short-range ordered cluster–cluster connection in metallic glasses than the fcc or hcp packing schemes.25 With consideration of the chemical effect, recent experimental and theoretical studies show more complicated cluster packing schemes in real multicomponent alloys. For example, chemical heterogeneity can lead to the co-existence of multiple cluster packing schemes giving rise to medium-range order in the same alloy.18
Illustrations of portions of a single cluster unit cell in the dense cluster packing model. (a) A two-dimensional representation of a dense cluster packing structure in the (100) plane of clusters illustrating the features of interpenetrating clusters and efficient atomic packing around each solute atom. Relaxations outside the plane of view cannot be shown in this two-dimensional representation. (b) A portion of a cluster unit cell of a <12-10-9> model system representing a Zr-(Al,Ti)-(Cu,Ni)-Be alloy. Zirconium solvent spheres (pink) form relaxed icosahedra around each solute atom. There is no orientational order among the icosahedral clusters. Adapted from Ref. 15 (© 2004 NPG).
The disordered atomic structure of metallic glasses has been examined extensively by various experimental methods, including X-ray and neutron diffraction, EXAFS and nuclear magnetic resonance.16,18,25,35 However, these experiments give only average and one-dimensional structural information, although plausible three-dimensional structural models can be reconstructed by trial and error using reverse Monte Carlo and ab initio molecular dynamics (MD) simulations.16,25,36,37 The main problem is that these methods cannot give unique atomic configurations, particularly for multicomponent alloys. In this sense, experimental observations of the local atomic structure of disordered metallic glasses are still lacking, and definite evidence of the local atomic order suggested by various theoretical models remains inconclusive. Recently, utilizing spherical aberration-corrected transmission electron microscopy, a coherent Angstrom beam electron diffraction technique has been developed to characterize the atomic structure of amorphous materials.38 With a ∼3.6 Å coherent electron beam, which is comparable to the size of single atomic clusters in metallic glasses, distinct diffraction patterns with a set of two-fold symmetric spots, analogous to the diffraction spectrum of a single crystal, can be frequently observed (Figure 3). The well-defined electron diffraction spots in the diffraction patterns from a sub-nanometer region provide direct evidence of local atomic order in disordered metallic glasses. Based on the diffraction patterns, the atomic structure of individual atomic clusters can be determined, which is consistent with structural predictions by MD simulations.38
Experimental scheme of Angstrom beam electron diffraction. The three-dimensional profile of a calculated electron nanoprobe with a full-width at half-maximum beam size of ∼0.36 nm is shown in the upper right inset (spherical aberration coefficient Cs = −0.002 mm, defocus Δf = 0 nm, convergence angle α = 3.3 mrad). The lower right insets show examples of the nanobeam size dependence of the electron diffraction patterns. A large number of diffraction patterns from nano-sized regions of a metallic glass were recorded by video during electron probe scanning. Adapted from Ref. 38 (© 2010 NPG).
Although research on the atomic structure of metallic glasses is a recent topic of intense discussion, the atomic configurations, particularly in multicomponent alloys, remain an unsolved mystery, and thus it is still a challenge to design BMGs based on atomic packing laws.
Dynamics of metallic glass formation
In view of the thermodynamic relationship between structure and phase stability in crystalline materials, the atomic origins of BMG formation have been discussed intensively from geometrical and topological perspectives of the dense atomic packing as introduced above. In principle, the formation of metallic glasses is a competition between the stability of supercooled liquids and the formation kinetics of rival crystalline phases.39,40,41 As both liquid stability and crystallization kinetics are time-related, and as metallic glasses are essentially out-of-equilibrium systems, the formation of BMGs involves structural evolution in time and thus may not be studied in terms of thermodynamics alone. Therefore, it seems to be more appropriate to explore the glass forming mechanism and glass forming ability from the perspective of the dynamics of supercooled liquids. Several kinds of temperature-dependent relaxations have been observed experimentally in metallic glasses. In the supercooled liquid state, α- or structural relaxation corresponds to an increase in shear viscosity and shear modulus during cooling, resulting in change of the glass formers from liquid behavior to viscoelastic behavior. In general, superior glass formers exhibit slower dynamics and a longer α-relaxation time at temperatures above the glass transition point. This is simply because the slow dynamics offers a low critical cooling rate for glass formation and, thus, has been used to explain the effect of alloying on the improved glass-forming ability of BMGs empirically.42,43,44 Nevertheless, the intrinsic correlation of the dynamic process with the atomic structure and chemistry of BMGs has not been well elucidated. It has been suggested that the development of icosahedral short-range order in the supercooled liquid regions may play an important role in glass formation because the densely packed atomic structure triggers slow dynamics near the glass transition point, a phenomenon known as dynamic arrest.42,43,45 Recently, MD simulations have suggested that the slow dynamic process may not be the only origin of the high stability of supercooled liquids and, instead, dynamic heterogeneity may play an important role in the excellent glass-forming ability of BMGs. Significant dynamic heterogeneity, coupled with structural and chemical inhomogeneity, has been observed in a Cu45Zr45Ag10 alloy.46 The fraction of the copper-centered full icosahedra and the number of coordinated silver atoms in each group are plotted against atomic mobility for a short time interval corresponding to fast relaxation and a long time interval for α-relaxation in Figure 4. Interestingly, a high icosaheral cluster population and silver-poor environments are responsible for slow dynamics. In contrast, a low icosahedral cluster population and silver-rich environments correspond to fast dynamics. The three-dimensional displacement maps in Figure 4 further visualize the isosurfaces of slow- and fast- dynamic regions, corresponding to partitioned silver-poor and -rich domains. The strong coupling between chemical and dynamic heterogeneity offers an alternative way to stabilize the supercooled liquid by partitioning the slow and fast dynamics regions, which can effectively prevent the nucleation of crystallites. As more or less chemical heterogeneity widely exists in multicomponent alloys, chemical and dynamic coupling seems to be a universal phenomenon in BMGs, which may suggest a new scheme that could be to elucidate the correlation between dynamic heterogeneity and glass-forming ability in multicomponent alloys, and provide new insight into the dynamic origins of BMG formation.
(a) Relationship between yield shear stress (Ty) and glass transition temperature (Tg). The solid line is the plot of the equation, Ty = 3R(Tg– RT)/V, where R is the gas constant. The symbols A to O represent the alloys listed in Table 1 of Ref. 56. (b) Two-dimensional plot of viscosity (η) as a function of T/T0 and σ/σ0, where T0 is the critical temperature and σ0 is the critical stress where η0 diverges in extrapolation to T = 0 K. The white curve represents the line for log10η0 = 5. Note that the lines with a constant value of η are self-similar.
Micromechanisms of mechanical properties
One of the most notable properties of BMGs is their extreme hardness and strength, which makes them attractive for applications where strength is critical. Nevertheless, the underlying deformation micromechanisms that govern the strength and ductility of BMGs remains poorly known.47 For crystalline metals and alloys, the factors controlling their mechanical properties have been well investigated through the development of dislocation and electronic theories, which can explain, in general, the atomic and electronic origins of the strength and ductility of crystalline materials. For disordered materials such as metallic glasses, however, the definite correlation between mechanical behavior and atomic and electronic structures has not been properly established. It has long been recognized that the mechanical properties of metallic glasses are closely related to the chemical and physical properties of their component elements.3 The significant differences in mechanical performance, such as strength and ductility, that are observed with changes in the chemical composition of metallic glasses indicate the existence of an intrinsic relationship between the mechanical properties and the atomic and electronic structures of metallic glasses. However, the underlying mechanisms have not been well understood and the physical picture appears to be much more complicated than that for crystalline materials.47
Shear transformation theory and shear transformation zones
The plastic deformation of metallic glasses at room temperature is known to be inhomogeneous both spatially and temporally, and to be carried by highly localized shear bands. With the increasingly intense scientific and technological interest in BMGs and efforts to improve their mechanical properties, it is essential to identify the underlying mechanisms responsible for ductility and strength. Historically, several theories have been developed to describe the heterogeneous plasticity of metallic glasses. These models are mainly based on two micromechanisms: deformation-induced dilatation or free volume mechanism, and a mechanism based on the cooperative shearing of atomic clusters termed shear transformation zones (STZs).48,49 Unambiguously, the free volume and STZ models provide simple and clear-cut explanations of the strain softening and thereby heterogeneous deformation of metallic glasses, and have been widely cited to explain various mechanical behaviors of metallic glasses qualitatively. However, they are unable to quantitatively describe the strength and ductility of BMGs. The appearance of a multidimensional potential energy surface, or potential energy landscape, of a disordered material can be related to the form of interatomic potentials. In combination with catastrophe theory, it is possible to describe how the geometry of the surface changes with the parameters in the potentials, and to provide universal scaling relations that can explain an unexpected connection between barrier heights, path lengths and vibrational frequencies, with applications to a wide variety of problems such as the mechanical behavior of metallic glasses.50
Deriving from the energy landscape theory and Frenkel scheme for the shear deformation of defect-free crystals, Johnson and Samwer proposed a cooperative shearing model for STZs.51 The Johnson–Samwer model was originally introduced to elucidate the temperature dependence of yield strength in the form of T2/3, yet it has also since been shown to provide an effective interpretation of ductility and strength of BMGs, which may pave the way to new quantitative insights into the atomic-scale mechanisms responsible for the mechanical properties of BMGs. By linking the cooperative shear model with classical deformation thermodynamics through the variable of the activation volume, the STZ volume is derived as a function of strain rate sensitivity and strength of metallic glasses, which are measurable by mechanical testing.52 The measured STZ volumes of BMGs vary from 2.5 to 6.6 nm3. According to the dense-packing hard-sphere model of metallic glasses, the STZs are estimated to include about 200–700 atoms, consistent with large-scale MD simulations. Moreover, the STZ volumes show an interesting correlation with the ductility of metallic glasses. The ductile BMGs possess large STZ volumes,52 which is similar to the relationship between ductility and dislocation cores in fcc metals, in which ductile metals have wide dislocation cores.
Metallic glass yielding versus shear stress-induced glass transition
One important phenomenon of metallic glass deformation and failure is the dramatic temperature rise in shear bands, which has been attributed as the origin of shear band formation and catastrophic failure in BMGs. Direct evidence for temperature rises within shear bands is provided by the unique fractograph of metallic glasses, called vein patterns, that can be reproduced by pulling apart two solid surfaces containing a thin viscous layer between them. Additionally, liquid droplets can frequently be observed on the fracture surfaces of metallic glasses. Because the failure of metallic glasses is usually caused by runaway sliding along a single shear band, the liquid droplets observed on the fracture surfaces demonstrate that the temperature rise is large enough to lead to the melting of shear bands during local shear deformation. However, the estimated width of the hot zone formed by plastic deformation is at least 100 nm,53 which is significantly larger than the shear band width measured by electron microscopy (5–20 nm).54,55 Thus, the observed temperature rise in shear bands and on fracture surfaces is most likely the result of concentrated plastic deformation and failure within very narrow deformation zones, but in itself cannot be the origin of yielding and shear band formation. This viewpoint is supported by the linear relation between yield strength and the glass transition temperature, as shown in Figure 5(a).56 It is known that the room-temperature yielding of BMGs relates to the formation of a principal shear band when the critical shear stress that a material can sustain is reached. According to the cooperative shearing model and recent computer simulations, the yield point of BMGs corresponds to the percolating propagation of a large number of local shearing events (i.e. STZs) under a critical shear strain.52,57,58 The transition from local shearing to macroscopic shear bands results from the dramatic increase in atom mobility and softening along a shear plane propagated by mechanical energy. Thus, the transition is akin to a process of stress-driven glass-to-liquid transition and the yielding of BMGs can be rationally presumed to occur at a critical point at which the accumulated internal energy by elastic deformation is sufficiently high to allow the transition from the glass state to the supercooled liquid to occur. Based on the effective temperature theory and fundamental thermodynamics, a theoretical linear relationship between yield stresses and glass transition temperatures that matches well with the experimental data can be derived. Therefore, yielding and shear band formation in BMGs are intrinsically processes of the shear stress-induced glass-to-liquid transition.56 An equivalent effect of shear stress and temperature on the glass transition can be confirmed from the viscosity diagram of a metallic glass (Figure 5(b)).59 This diagram was constructed on the basis of systematic MD simulations of steady viscous flow at various temperatures and shear strain rates. Liquid-like behavior with low viscosity can be achieved by either temperature or shear stress, or a combination of both effects.
Correlation between atomic mobility of copper atoms and their local structural environments in Cu45Zr45Ag10 at 800 K. The copper atoms are sorted into 20 groups in increasing order of displacement. In each group, the percentage of <0,0,12,0> polyhedra and number of coordinated silver atoms are plotted with (a) a short time interval of 1.5tα′, and (b) a long time interval of 1.5tα′, where the shear stress and temperature as the independent variables are plotted on the x and y axes, respectively. (c) Three-dimensional mean-square displacement map of all atoms based on propensity for motion under the conditions observed in (b). The isosurfaces indicate the slow- and fast-dynamics regions where Δr2 is less than 25 Å2 (blue regions) and more than 80 Å2 (green to red regions). (d) Three-dimensional map showing isosurfaces of the slow-dynamics regions and the distribution of silver atoms (pink balls). The blue slow-dynamics regions are apparently silver-poor regions. The cube has the dimensions of 53×53×53 Å3; the color bars in (c) and (d) show the range from fast (red) to slow (blue) dynamics. Adapted from Ref. 46 (© 2010 APS).
Ductility and composite effects
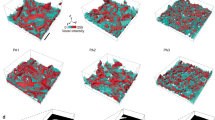
Although BMGs possess very high strength compared to their crystalline counterparts, they generally suffer from low ductility at low temperature. Room-temperature plastic deformation of metallic glasses has been known to occur through shear band movement, in which plastic flow driven mainly by shear stresses is localized within a nano-scale zone.3,48,49 Due to structural and/or thermal softening, these bands are preferential sites for further plastic flow and lead to final failure in a brittle manner that typically breaks a sample along a single shear band without detectable plastic strains. Therefore, highly localized shearing and resultant strain softening are responsible for the poor ductility of BMGs. It has been recognized that the ductility improvement of BMGs largely depends on suppression of the localized strain softening caused by shear bands. Microstructural inhomogeneity caused by phase separation and crystallization can arrest persistent slip on individual shear bands and give rise to global plasticity by activating multiple shear bands when the BMGs are loaded under uniaxial compression.32,33,54 However, these compressively ductile BMGs all lack tensile ductility, probably because in tension the opening stress on the shear bands enhances strain softening and instability, whereas under compression, an operating shear band is subject to a normal stress that closes the band and enhances the frictional forces induced by microstructural variations. A straightforward strategy is to introduce ductile crystalline phases into BMGs to form BMG-based composites in which the work hardening of the crystalline phases caused by dislocation multiplication- or deformation-induced phase transitions61 can compensate for the strain softening of shear bands and block catastrophic slip along a single shear band to give high tensile plasticity. The accessibility of this idea was first demonstrated by the dramatic improvement in the tensile ductility of titanium–zirconium-based BMG composites containing a ∼50 vol% dendritic phase.60 The composites possess a maximum elongation of ∼13%, which is comparable to that for ductile multiphase alloys, such as steels and aluminum alloys, and maintain a high yield stress of 1.2–1.5 GPa (Figure 6).
Enhanced room-temperature tensile ductility of Zr36.6Ti31.4Nb7Cu5.9Be19.1 (DH1), Zr38.3Ti32.9Nb7.3Cu6.2Be15.3 (DH2) and Zr39.6Ti33.9Nb7.6Cu6.4Be12.5 (DH3). (a,b) Backscattered scanning electron micrographs showing the microstructure of DH1 (a) and DH3 (b), where the dark contrast corresponds to the glass matrix and the light contrast to the dendrites. (c) Engineering stress–strain curves for Vitreloy 1, DH1, DH2 and DH3 in room-temperature tension tests. (d) Optical micrograph of necking in DH3. (e) Optical micrographs showing an initially undeformed tensile specimen contrasted with DH2 and DH3 specimens after tension testing. (f) Scanning electron micrograph of the tensile surface in DH3. (g,h) Scanning electron micrographs of necking in DH2 (g) and DH3 (h). (i) Brittle fracture representative of all monolithic BMGs. Adapted from Ref. 60 (© 2008 NPG).
Recent advances in applications
The applications of metallic glasses have been covered in several review articles and comprehensive books.62,63,64,65 For example, BMGs have been used as one of the best soft magnetic materials for a wide range of applications from electronic devices to automobiles and long-distance electric power transmission. Combining high strength and low density, BMGs have also been exploited as light-weight structural materials for applications in which weight and strength are critical. As these applications have been detailed in previous publications, the present review focuses on recent progress in applications in biomedicine, nanotechnology and microelectromechanical systems (MEMS).
Biomedical materials
Metals and alloys have been widely used as biomedical materials and are indispensable in the medical field. For example, about 70% of the structural materials employed in implants are metallic materials that are used to replace hard tissues or as hard-tissue prostheses, including bone screws, bone plates, artificial hip joints, knee joints and dental implants. The advantages of BMGs compared with conventional crystalline metals and alloys include superior strength, high elasticity and excellent wear and corrosion resistance, attributable to the lack of grain boundaries and crystal defects that usually lead to weakening of material strength, intergranular corrosion and stress-corrosion cracking in biological environments. Corrosion testing of BMGs has demonstrated that these materials have much better corrosion properties in physiological solution compared to many common metallic biomaterials.66 Moreover, the relatively flexible composition of BMGs and the large number of glass formers makes it possible to design and select glassy alloys without toxic elements for full biocompatibility. Recently, in vitro and in vivo experiments have demonstrated that BMGs are, in general, nontoxic to cells and compatible with cell growth and tissue function.67,68,69 Importantly, BMGs have much lower Young modulus than crystalline metals, allowing BMGs to be more compatible with bone, reducing the stress-shielding effect that can cause disuse atrophy of cortical bone. Therefore, BMGs possess attractive properties for load-bearing biomedical-implant applications. Bulk metallic glasses have also been suggested for application as soft tissue stents due to their high flexibility, providing enhanced compliance with blood vessel biomechanics and thereby minimal damage to vessels.68 More recently, magnesium-based BMGs have been developed for application as biodegradable implants.70 In addition to their higher strength and elasticity in comparison with the crystalline biodegradable magnesium-based alloys, biodegradable metallic glasses also show a distinct reduction in hydrogen evolution in vivo, which is a general problem that occurs as a result of biocorrosion in physiological solution and forms an unwanted gas pocket around the implants (Figure 7). Owing to the broad solubility of the glassy alloys, the chemical composition of BMGs can also be optimized to match the biocorrosion characteristics of the environment, providing control over degradation and hydrogen evolution rates, which is very difficult to achieve using crystalline alloys.
Animal studies of magnesium-based metallic glass in comparison with a crystalline magnesium alloy reference sample. (a–d) Glassy Mg60Zn35Ca5 (a,c) and crystalline magnesium alloy reference (WZ21) (b,d) in two types of porcine abdominal tissue (muscle after 27 days (a,b) and subcutis after 91 days (c,d) of implantation). All samples show a typical fibrous capsule foreign-body reaction (indicated by white arrows), but only the crystalline samples (implanted discs indicated by dashed lines) show pronounced hydrogen evolution (area between discs and fibrous capsules indicated by black arrows). Adapted from Ref. 69 (© 2010 Springer Science+Business Media).
Nanotechnology and MEMS
Like other glassy materials, such as oxide glasses and amorphous polymers, BMGs have a wide supercooled liquid range when heated from room temperature. Within this temperature window, BMGs transform into a viscous supercooled liquid with significant softening and, thus, can be shaped by Newtonian viscous flow under very small applied forces. This unique property of glassy materials endows BMGs with extraordinary formability and superplasticity, comparable to those of polymers and window glasses. Bulk metallic glasses are quite stable in the supercooled state and, after thermal processing, can be slowly cooled back to the strong glassy state with negligible volume shrinkage. This outstanding thermal formability of BMGs has recently been exploited for applications in nanotechnology and MEMS.71,72,73,74,75,76,77,78
In micro- and nano-machines, as well as MEMS, three-dimensional structures or surface nano-patterns are frequently required, which are traditionally fabricated by lithography and chemical or ion etching. Such processes originate in semiconductor technology and are generally limited to silicon and related materials. The micro- and nano-fabrication of metallic materials for such applications is either expensive or lacks the accuracy required for precision processes.77 Utilizing the excellent thermal formability of BMGs, supercooled liquid fabrication provides an alternative and economic approach for the fabrication of micro- and nano-sized metallic parts and surface patterns for MEMS and micro- and nano-machines. By applying plastic processing techniques, micro- or nano-patterns can be easily transferred to BMG surfaces from stiff dies and molds by thermal imprinting (Figure 8(a–b)). The sub-nanoscale structural homogeneity also makes patterned BMGs of interest for optical applications.71 Using a die-forging technique, free-standing BMG micro-parts of as small as 1 μm have been produced for micro-machines (Figure 8(c–d)).71,75 The ultra-high strength and lack of grains and grain boundaries give these metallic glass micro-parts mechanical performance superior to that of their crystalline counterparts, which are limited by the characteristic length of their microstructures. Sputtered BMG films have also been used to fabricate actuators and micro-cantilevers for MEMS applications.74 Recently, the dimensions of BMG patterns and parts have been further reduced to scales on the order of tens of nanometers by superplastic deformation76 and thermoplastic forming.78,79 Metallic glass nanowires fabricated by these methods show interesting multi-harmonic oscillations with possible applications in mechanical and magnetic sensors. The development of such nano-sized BMG structures may lead to a host of applications of BMGs in nanotechnology and bionanotechnology.
(a) Atomic force microscopy image of a (100) silicon die with concave nano-pyramids. (b) Convex nano-pyramids of a BMG forged with the die in (a). (c) Die of gears fabricated using a focused ion beam system with a zirconium-based BMG. (b) Die-forged micro gears of a platinum-based BMG (Courtesy of Y. Saotome, Tohoku University, Japan).
Summary and perspectives
Research over the past 20 years has produced a large number of BMGs and composites in various alloy systems, rousing intense research interest for the search for novel physical and chemical phenomena in non-equilibrium, disordered, multicomponent solids. Bulk metallic glasses hold great promise for structural and functional applications and are viewed as one of the most important metallic materials owing to their unique properties of extreme strength at room temperature and high flexibility at high temperature. However, as outlined in this review, many fundamental questions remain and our understanding of the properties and structures of BMGs is far from comprehensive. Researchers are continuing to explore the atomic-scale mechanisms of BMG formation and to search for new bulk glassy alloys and composites with improved glass-forming ability as well as enhanced strength and ductility. Recent applications of BMGs in biomedicine, MEMS and nanotechnology have opened innovative fields for future intense research and may stimulate the creation of new industries.
References
W. Klement, R. H. Willens, P. Duwez, Nature 187, 869 (1960).
H. S. Chen, C. E. Miller, Mater. Res. Bull. 11, 49 (1976).
H. S. Chen, Rep. Prog. Phys. 43, 353 (1980).
H. S. Chen, Acta Metall. 22, 1505 (1974).
A. J. Drehman, A. L. Greer, D. Turnbull, Appl. Phys. Lett. 41, 716 (1982).
H. W. Kui, A. L. Greer, D. Turnbull, Appl. Phys. Lett. 45, 615 (1984).
A. L. Greer, Science 267, 1947 (1995).
A. Inoue, T. Zhang, T. Masumoto, Mater. Trans. JIM 31, 177 (1990).
A. Inoue, Acta Mater. 48, 279 (2000).
A. Peker, W. L. Johnson, Appl. Phys. Lett. 63, 2342 (1993).
A. L. Greer, Nature 366, 303 (1993).
I. Gutzow, D. Kashchiev, I. Avramov, J. Non-Cryst. Solids 73, 477 (1985).
F. C. Frank, Proc. R. Soc. A 215, 43 (1952).
T. Egami, Y. Waseda, J. Non-Cryst. Solids 64, 113 (1984).
D. B. Miracle, Nature Mater. 3, 697 (2004).
X. K. Xi, L. L. Li, B. Zhang, W. H. Wang, Y. Wu, Phys. Rev. Lett. 99, 095501 (2007).
D. B. Miracle, Acta Mater. 54, 4317 (2006).
T. Fujita et al., Phys. Rev. Lett. 103, 075502 (2009).
J. D. Bernal, Nature 185, 68 (1960).
J. D. Bernal, Proc. R. Soc. A 280, 299 (1964).
P. H. Gaskell, Nature 276, 484 (1978).
P. H. Gaskell, J. Non-Cryst. Solids 351, 1003 (2005)
P. H. Gaskell, J. Non-Cryst. Solids 32, 207 (1979).
A. Inoue et al., Mater. Trans. JIM 39, 318 (1998).
H. W. Sheng, W. K. Luo, F. M. Alamgir, J. M. Bai, E. Ma, Nature 439, 419 (2006).
M. W. Chen, T. Zhang, A. Inoue, A. Sakai, T. Sakurai, Appl. Phys. Lett. 75, 1697 (1999).
M. W. Chen, I. Dutta, T. Zhang, A. Inoue, T. Sakurai, Appl. Phys. Lett. 79, 42 (2001).
Y. Q. Cheng, E. Ma, H. W. Sheng, Phys. Rev. Lett. 102, 245501 (2009)
T. H. Kim et al., Phys. Rev. Lett. 95, 085501 (2005).
T. Fukunaga et al., Intermetallics l4, 893 (2006).
T. Ichitsubo et al., Phys. Rev. Lett. 95, 245501 (2005).
J. Das et al., Phys. Rev. Lett. 94, 205501 (2005)
Y. H. Liu et al., Science 315, 1385 (2007).
W. Dmowski, T. Iwashita, C.-P. Chuang, J. Almer, T. Egami, Phys. Rev. Lett. 105, 205502 (2010).
D. Ma, A. D. Stoica, X. L. Wang, Nature Mater. 8, 30 (2009).
D. A. Keen, R. L. McGreevy, Nature 344, 423 (1990).
R. L. McGreevy, J. Phys.-Condens. Mat. 13, R877 (2001).
A. Hirata et al., Nature Mater. 10, 28 (2011).
D. Turnbull, Contemp. Phys. 10, 473 (1969).
C. A. Angell, MRS Bull. 33, 544 (2008).
Z. P. Lu., C. T. Liu, Phys. Rev. Lett. 91, 115505 (2003)
Y. Q. Cheng, E. Ma, H. W. Sheng, Appl. Phys. Lett. 93, 111913 (2008).
S. M. Chathoth, B. Damaschke, M. M. Koza, K. Samwer, Phys. Rev. Lett. 101, 037801 (2008).
Y. T. Shen, T. H. Kim, A. K. Gangopadhyay, K. F. Kelton, Phys. Rev. Lett. 102, 057801 (2009).
H. Tanaka, J. Phys. Condens. Matter 15, L703 (2003).
T. Fujita et al., Phys. Rev. B 81, 140204(R) (2010).
M. W. Chen, Ann. Rev. Mater. Res. 38, 445 (2008).
F. Spaepen, Acta Metall. 25, 407 (1977).
A. S. Argon, Acta Metall. 27, 47 (1979)
D. J. Wales, Energy Landscapes with Applications to Clusters, Biomolecules and Glasses (Cambridge University Press, 2003).
W. L. Johnson, K. Samwer, Phys. Rev. Lett. 95, 195501 (2005).
D. Pan, A. Inoue, T. Sakurai, M. W. Chen, PNAS 105, 14769 (2008).
J. J. Lewandowski, A. L. Greer, Nat. Mater. 5, 15 (2006).
M. W. Chen, A. Inoue, W. Zhang, T. Sakurai, Phys. Rev. Lett. 96, 245502 (2006).
P. E. Donovan, W. M. Stobbs, Acta Metall. 29, 1419 (1981).
Y. H. Liu et al., Phys. Rev. Lett, 103, 065504 (2009).
P. Schall, D. A. Weitz, F. Spaepen, Science 318, 1895 (2007).
S. G. Mayr, Phys. Rev. Lett. 97, 195501 (2006).
P. F. Guan, M. W. Chen, T. Egami, Phys. Rev. Lett. 104, 205701 (2010).
D. C. Hoffmann et al., Nature 451, 1085 (2008).
S. Pauly, S. Gorantla, G. Wang, U. Kühn, J. Eckert, Nature Mater. 9, 473 (2010).
W. H. Wang, C. Dong, C. H. Shek, Mater. Sci. Eng. R. 44, 45 (2004)
C. Suryanarayana, A. Inoue, Bulk Metallic Glasses (CRC Press, 2010).
W. H. Wang, Adv. Mater. 21, 4524 (2009)
M. Miller, P. K. Liaw eds, Bulk Metallic Glasses: An Overview (Springer, 2008).
M. L. Morrison et al., J. Biomed. Mater. Res. A 74A, 430 (2005).
S. Buzzi et al., Intermetallics 14, 729 (2006).
J. Schroers, G. Kumar, T. M. Hodges, S. Chan, T. R. Kyriakides, JOM 61, 21 (2009).
M. D. Demetriou et al., JOM 62, 83 (2010).
B. Zberg, P. J. Uggowitzer, J. F. Löffler, Nature Mater. 8, 887 (2009)
Y. Saotome, K. Ito, T. Zhang, A. Inoue, Scripta Mater. 44, 1541 (2001).
Y. Saotome et al., Intermetallics 10, 1241 (2002).
J. Schroers, T. Nguyen, S. O'Keeffe, A. Desai, Mater. Sci. Eng. A 898, 449–451 (2007).
H.-W. Jeong, S. Hata, A. Shimokohbe, J. Microelectromech. S. 12, 42 (2003).
N. Nishiyama, A. Inoue, Mater. Trans. 40, 64 (1999).
K. S. Nakayama et al., Adv. Mater. 22, 872 (2010).
G. Kumar, A. Desai, J. Schroers, Adv. Mater. 23, 461 (2011).
G. Kumar, H. X. Tang, J. Schroers, Nature 457, 868 (2009)
N. Nishiyama et al., Intermetallics 18, 1983 (2010)
Q. Zhang, W. Zhang, A. Inoue, Mater. Trans. 48, 3031 (2007)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Chen, M. A brief overview of bulk metallic glasses. NPG Asia Mater 3, 82–90 (2011). https://doi.org/10.1038/asiamat.2011.30
Published:
Issue Date:
DOI: https://doi.org/10.1038/asiamat.2011.30
This article is cited by
-
Enhanced Radiation Damage Tolerance of Amorphous Interphase and Grain Boundary Complexions in Cu-Ta
JOM (2024)
-
Preparation, Microstructure, and Mechanical Properties of Bulk Metallic Glass Composite Containing In Situ-Formed Dendrites and Ex Situ Tungsten Particles
Journal of Materials Engineering and Performance (2024)
-
A molecular dynamics study on the mechanical response of thermal-pressure rejuvenated CuxZr100−x metallic glasses
Scientific Reports (2023)
-
Composition dependence of polyamorphic transition in Pd–Ni–P metallic glasses
Science China Materials (2023)
-
A comparative study on mechanical polishing and laser polishing of laser-nitrided Zr-based metallic glass surface
The International Journal of Advanced Manufacturing Technology (2023)