Introduction

Scanning laser polarimetry1 (SLP) is one of the available methods for imaging the retinal nerve fibre layer (NFL). Its working principle is based on the retardation of polarized light. The microtubules of the axons of the ganglion cells in the NFL show form birefringence. Owing to their ordering in parallel bundles, this birefringence causes a net change in retardation of passing light. The amount of retardation is therefore related to the thickness of the NFL.2, 3

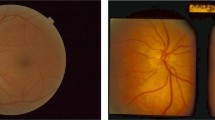
The GDx (Carl Zeiss Meditec Inc., Dublin, CA, USA), a device based on SLP, was developed for the detection and follow-up of glaucoma. Glaucoma is a progressive optic neuropathy with an acquired loss of retinal ganglion cells and their axons, leading to local and/or diffuse thinning of the NFL and corresponding visual field defects.4, 5 If specific bundles of nerve fibres disappear, they leave a local, wedge-shaped defect in the NFL. Such defects, typically running toward or touching the optic disc border,6 result in a spatially correlated reduction of the measured NFL. These defects are almost always pathological, although not necessarily glaucomatous. These wedge-shaped defects are also found in images acquired with the GDx.7, 8 An example is shown in Figure 1, where the image acquired with the GDx is superimposed on a red-free fundus photograph of an eye with an inferonasal wedge-shaped defect that is clearly visible in both image modalities.

Figure 1
figure 1

Example of an image acquired with the GDx NFA superimposed on a red-free fundus photograph of the same eye. Both images clearly show a wedge-shaped defect, located inferonasally.

Full size image

Many studies have assessed how well the GDx distinguishes healthy from glaucomatous eyes, often expressed in sensitivity and specificity.9, 10, 11, 12 Most of these studies explored the standard parameters provided by the GDx (described elsewhere13) or combinations of these (some including the built-in classifier named The Number). Despite their fair to excellent performance, these parameters may be quite insensitive to wedge defects, especially narrow ones, since they are based either on general statistics of measurements along an ellipse around the optic disc or on measurements in a fairly large area, such as an image quadrant. The statistics used to calculate the parameters thus neglect the finer spatial relationship between measurements at the pixel level. Automatically detecting wedge defects may therefore assist in diagnosing glaucoma.

A sectoral analysis was tried to overcome the spatial insensitivity of the current statistics to detect wedge defects. In this approach, the area around the optic disc was divided into sectors, varying in size. Statistics, such as the average NFL thickness, were then based on these sectors. A discriminant analysis based on these sectors might potentially outperform the conventional parameters in classifying healthy eyes from eyes with early to moderate visual field defects, but these results were not tested on independent data sets.14, 15 However, it was shown that sectoral analysis failed to specifically detect and locate local defects (Kremmer S et al. IOVS 2002; 43; ARVO E-Abstract 1012). We think that such a sectoral analysis has at least two major inherent limitations: first, sampling theory dictates that the sampling frequency should be more than twice the highest frequency in the sampled signal to allow correct reconstruction.16 For detecting wedge defects, the size of the sectors used for the analysis should be smaller than half the width of the smallest wedge defect to be detected, since otherwise no sector may be completely covered by the wedge defect. For the previously mentioned 30°, this means that only the largest wedges (60°) will be accurately detected. Secondly, many healthy eyes show ‘splitting’ of their arcuate bundles into two or more arms with a thinner NFL in between.17 The sector analysis would erroneously flag these thinner areas as abnormal.

Recently, we proposed a new, holistic method that detects wedge defects based on their edges.18 In this paper, the sensitivity and specificity of this automated method is tested on both clear and less clear cases of local defects compared to human observers. For some typical prevalences, positive and negative predictive values (PPV and NPV) are derived as well.

Methods

Samples

In all, 31 eyes of 25 healthy subjects and 37 eyes of 26 glaucoma patients were imaged for the current experiments. The mean age of the healthy subjects and the glaucoma patients was 58 years (standard deviation (SD) 10) and 60 years (SD 9), respectively, which was not statistically significantly different. In the healthy and glaucoma group, 11/25 (44%) and 10/26 (39%) were men, respectively. All subjects were of white ethnicity. They all had a visual acuity of 20/40 or better. Subjects were enrolled in this study subsequently.

Healthy subjects were recruited either from an ongoing longitudinal follow-up study or from employees of the Rotterdam Eye Hospital, their spouses, and friends. All healthy subjects had normal visual fields, healthy-looking optic discs, and intraocular pressures of 21 mmHg or less. None had any significant history of ocular disease, including posterior segment eye disease and corneal disease, relatives in the first and/or second degree with glaucoma, systemic hypertension for which medication was used, diabetes mellitus, or any other systemic disease. Per subject, we imaged one random eye. For 17 patients, the fellow eye was also measured. The mean Mean Deviation (MD) and mean Pattern Standard Deviation (PSD) were −0.12 dB (SD, 1.16 dB; range, −3.07–1.69 dB) and 1.61 dB (SD, 0.40 dB; range, 1.13–3.00 dB), respectively.

Glaucoma patients were recruited consecutively from an ongoing longitudinal follow-up study or after referral by a glaucoma specialist (HGL) when a localized NFL defect was suspected. All glaucoma patients had a reproducible glaucomatous visual field defect and a glaucomatous appearance of the optic disc, as judged by the same glaucoma specialist. Patients with any significant coexisting ocular disease, including posterior segment eye diseases and corneal diseases, or systemic diseases with possible ocular involvement, such as diabetes, were excluded. The mean MD and mean PSD were −6.73 dB (SD, 5.80 dB; range, −21.83 to −0.33 dB) and 8.31 dB (SD, 4.39 dB; range, 1.51–16.25 dB), respectively. As this study addressed the performance of the automated detection compared to human observers, red-free fundus photographs were not used to validate the presence or absence of a wedge.

The research followed the tenets of the Declaration of Helsinki. Informed consent was obtained from the subjects after explanation of the nature and possible consequences of the study. The research was approved by the institutional human experimentation committee.

Since our algorithm did not distinguish between superior and inferior halves of the NFL, we split each image into two (superior and inferior) halves, resulting in 136 half images. Besides the advantage of doubling our sample of images, this also reduced the risk of scoring a wedge defect at the wrong location. For example, in a complete image, if a wedge was present superiorly and the algorithm detected a wedge inferiorly, the image would be correctly classified as abnormal, although the algorithm failed. Using half-images prevents this.

Image acquisition

We used a modified GDx to assess the NFL thickness. The modification entailed that our device was equipped with a variable cornea compensator,19 which could be optimally adjusted for each individual eye. This individual compensation greatly enhanced the visibility of wedge defects.8 The recorded images consisted of 256 × 256 pixels, at a quantization of 8 bits. The viewing angle was 15° × 15°, yielding a sampling density of approximately 59 pixels/mm. The standard colour coding of the GDx software was not used; instead, all images were processed in a grey-scale.

The prototype GDx was less user-friendly compared to the commercially available device. This explains the availability of images of both eyes for some subjects, while for most subjects only one randomized eyes was imaged. At first, both eyes of all subjects were imaged. Since this proved to be too time-consuming, only one randomized eye was imaged for subsequent subjects.

Expert classification

We noticed that some wedge defects were barely visible in polarimetric images, notably due to very small retardation differences between the defect and its surrounding, a blurred appearance of the edges of the wedge defect or occlusion of the edges by blood vessels. Accordingly, we defined four classes of wedge defects (Table 1; Figure 2 shows an example of classes 1 and 3) and asked two experts to independently classify each (grey-scale) image, including those of healthy eyes. There was at least 10 months between referral and classification. The experts then conferred to reach agreement on those cases where they initially rated the images differently.

Table 1 Class definitions of wedge-shaped defects and the number of samples per class after agreement was reached
Full size table
Figure 2
figure 2

Examples of (a) class 1 (wedge between 6 and 7 o’clock) and (b) class 3 (wedge between 12 and 1 o’clock).

Full size image

The tenet of this research was to test whether the automated method identified wedge defects in polarimetric images similarly as human expert observers. We did not intend to compare the ability to detect wedge defects between red-free fundus photographs and polarimetric images.

Model

Figure 3a shows the TSNIT graph (a graph of the NFL thickness at a distance from the optic disc, in temporal, superior, nasal, inferior, temporal order) of an ‘ideal’ eye. In this model, the inferior and superior halves were considered similar. As virtually all wedge-shaped defects are located in the temporal half of the NFL,20 the model disregarded the inferonasal and superonasal parts with the added benefit of better fine-tuning of the remaining part. An example of a typical wedge defect in the remaining part (either inferotemporal or superotemporal) of the TSNIT graph is shown in Figure 3b. In reality, the steep edges shown here are often degraded, but the gradient is still large for both edges of the wedge defect (as shown in Figure 3c). These edges were the key features of the wedge defects that we used to detect them. Additionally, the edges were required to extend over a larger region of the image, running approximately straight from the outside of the image towards the optic disc.

Figure 3
figure 3

(a) TSNIT graph of an ‘ideal’ eye. (b) TSNIT graph of a typical wedge (superotemporal) as compared to original NFL (dashed line). (c) Degraded wedge, but the gradient (dashed line) is still large.

Full size image

We thus modelled local defects as an area limited by two approximately straight edges with ‘considerable’ gradient and opposing directions. We fine-tuned the sensitivity and specificity of the algorithm by quantifying the required magnitudes of the gradient.

Algorithm

In this section, we shall give a brief overview of our algorithm. A more detailed description can be found elsewhere.18 The complete algorithm consisted of three steps:

  1. 1

    Preprocessing.

  2. 2

    Edge detection.

  3. 3

    Matching edges.

In the first step, the blood vessels were detected21 and the NFL at those locations was estimated by interpolating the surroundings of the vessels (see Figure 4a). The image was then transformed into a polar image, as shown in Figure 4b. In the transformed image (see Figure 4c), the position of a pixel along the x-axis corresponded to the angle of the pixel in the original image with respect to the centre of the optic disc. The position along the y-axis corresponded to the distance to the optic disc in the original image. Subsequently, the image was morphologically filtered to remove texture. An example is shown in Figure 5, in which only the interesting, inferior area is shown. To handle wedges overlapping the edge of the temporal half, the algorithm processes a slightly larger area.

Figure 4
figure 4

Image transformation. (a) Original image, but with estimated NFL at blood vessel locations. (b) Schematic illustration of image transformation. (c) Polar representation. The top of the image corresponds to the border of the optic disc. The letters denote the corresponding location of the horizontal axis. The wedge is located just to the right of the letter I.

Full size image
Figure 5
figure 5

Filtered image (only the inferior part of the original image of Figure 4a is shown, corresponding to the left half of Figure 4c), in which the texture has been removed.

Full size image

The second step detected possible wedge edges in the polar image. The algorithm located locally strong, approximately straight edges. The result of the edge detection is shown in Figure 6. For each of the located edges, the absolute strength was defined based on the average gradient at the location of that edge. This absolute strength was then divided by the average NFL thickness at the edge location, yielding the relative strength. We defined two thresholds on the strength of the edges, a high one for ‘strong’ edges and a lower one for ‘weak’ edges. Strong edges only needed to exceed a certain relative strength. Weak edges had to exceed both a relative and an absolute strength threshold, to compensate for the worse signal-to-noise ratio. This two-threshold approach has the advantage over one threshold for both edges that one of the edges is allowed to be visible relatively badly.

Figure 6
figure 6

Located edges superimposed on Figure 5. Black lines show the location of a gradient in one direction, and white lines in the opposing direction.

Full size image

In the final step, the edges were combined. To mark an area as a wedge defect, one of the edges had to be ‘strong’, while the other had to be at least ‘weak’. Also, the distance between the two edges had to be larger than the width of a vessel, with a maximum angle of 60°.20 The area within the two edges is then considered to be a wedge. In Figure 7, this is shown for the example image. The final result is also shown on the original image in Figure 8a and another example is presented in Figure 8b. Figure 8c shows the detection result on the image of Figure 1.

Figure 7
figure 7

Classification and combination of the edges shown in Figure 6. The solid line is a strong edge, while the dashed lines are weak edges. Edges not exceeding the weak threshold are not shown. A strong edge in one direction is combined with a weak edge in the opposing direction to form the detected wedge, indicated by the grey area.

Full size image
Figure 8
figure 8

(a) Detection results outlined (white) on the original example image. (b) Another example of a detected wedge. (c) Detection result on the image in Figure 1.

Full size image

Statistics

To quantify the agreement between the experts, the intraclass correlation coefficient ICC(3,1)22 was calculated. Additionally, the weighted Kappa was calculated, with equal weights. Note that weighted Kappa with squared weights is very similar to the calculated ICC.

First, only classes 1 and 4 (the clear cases) were considered. A true-positive was defined as a detected wedge in the half-image in which the experts agreed on class 1, according to Table 1. A false-negative was defined as an undetected wedge in the half-image in which the experts agreed on class 1. Similarly, true-negative and false-positive results were defined based on the half-images of class 4. The sensitivity was defined as the fraction of true-positive cases for all half-images of class 1. The specificity was defined as the fraction of true-negative cases for all half-images of class 4. The performance of the algorithm was described by an ROC curve, which plots the sensitivity as a function of 1-specificity. The ROC was summarized by the area under the curve and its standard error (SE).23

To assess the performance of each expert, the other expert was considered as the ‘gold standard’. Again, only the half-images that were rated by the other expert as class 1 or 4 were considered. A rating of either class 1 or class 2 by the expert under consideration was interpreted as ‘wedge defect present’, class 4 as ‘no wedge defect present’. Class 3 was interpreted once as ‘wedge defect present’ and once as ‘no wedge defect present’, resulting in two measures per expert.

Similarly, classes 1 and 2 vs class 4 were considered. Specificity and sensitivity measures were calculated and shown in an ROC graph. The experts’ performance for these classes was again computed. In addition, for these classes, both PPV (the fraction of wedge defects for all positive test results) and NPV (the fraction of healthy eyes for all negative test results) were calculated as a function of the overall performance (the fraction of correct test results), again based on the agreed ratings.

Results

The results of the classification made independently by the two experts have been listed in Table 2. The corresponding intraclass correlation coefficient ICC(3,1) was 0.77, while the inter-rater agreement, expressed as (equally) weighted Kappa, was 0.69.

Table 2 Agreement between the two experts
Full size table

By systematically adjusting the parameters of the algorithm, we were able to change the sensitivity and specificity. This resulted in the ROC curve of Figure 9, which shows the results for class 1 (15 cases) vs class 4 (95 cases; classes 2 and 3 were disregarded). For example, at a specificity of 93%, the algorithm yielded a sensitivity of 80%. The area under the ROC was 0.95, with an SE of 0.041. The experts’ scores have been indicated by crosses.

Figure 9
figure 9

ROC curve for class 1 vs class 4. The crosses show the performance of the experts, with the other experts’ judgment used as the ‘gold standard’.

Full size image

A similar graph was created for class 1 and 2 (20 cases total) vs class 4 (95 cases, disregarding class 3), resulting in Figure 10. Again, the experts’ scores have been indicated by crosses. This algorithm yielded, for example, a sensitivity of 55% at a specificity of 95% (Kappa=0.54). The area under this ROC was 0.89, with an SE of 0.049.

Figure 10
figure 10

ROC curve for class 1 and 2 vs class 4. The crosses show the performance of the experts, with the other experts’ judgment used as the ‘gold standard’.

Full size image

The PPV and NPV for class 1 and 2 vs class 4 have been shown in Figure 11 for various prevalences.

Figure 11
figure 11

(a) PPV and (b) NPV as a function of the overall accuracy for different prevalences for class 1 and 2 vs class 4. The arrows show the direction in which the PPV or NPV changes for an increase of the true and false-positive rate. Note the different scales for PPV and NPV.

Full size image

Discussion

Our algorithm was capable of automatically detecting wedge-shaped defects in polarimetric images of the NFL with a sensitivity of 55% and a specificity of 95%. The intraclass correlation coefficient of 0.77 that we found for our experts can be considered as ‘good’.

Including class 2 wedge defects (ie those with one fuzzy edge) impaired the detection results, as indicated by the deteriorated ROC curve in Figure 10 as compared to Figure 9. These wedges did not closely follow the underlying model of our algorithm. Comparing the crosses in Figures 9 and 10 shows that inclusion of class 2 wedge defects also markedly reduced the experts’ performance.

Our algorithm yielded a sensitivity of 55% at a specificity of 95% on classes 1 and 2 vs class 4. Since the prevalence of wedge defects is smaller than 0.5, a high specificity for detecting them is desirable to prevent many false-positives detection results. For a specific population, predictive values are important, since they denote the confidence of the outcome of the test. As shown in Figure 11, a prevalence of 20%20 gives a PPV of 80% and a NPV of 89% for an overall accuracy of 87%. Note that this is based on a sensitivity of 50% and a specificity of 97%. The optimal setting also depends on weighing the relative importance of false-positive and false-negative classifications, but we did not further investigate this.

The use of half-images and including both eyes of (some) people may result in a bias if a correlation between the ease of detection of both our automated detection algorithm and human observers in half-images of the same person exists. To our knowledge, such a correlation has not been reported. On the other hand, this approach significantly increases the number of samples, due to the analysis of half-images instead of full images and the inclusion of both eyes if images were available. Additionally, the use of half-images increased the required spatial correlation between true and detected wedges, since a detected superior wedge is not matched to a true inferior wedge. We therefore feel that the advantages of better validation due to the use of half-images of all available images outweigh the possibility of introducing a small bias.

One major advantage of this algorithm is that its feedback to the operator is very easy to interpret. The outline of the detected wedge defect is simply shown on the image to alert the clinician, who may then use other sources of information (eg visual fields, red-free photographs) to verify its existence.

The new commercially available GDx with automated variable cornea compensation (GDx VCC) has a smaller number of pixels (128 × 128 pixels instead of 256 × 256 pixels), but a larger field of view (20° instead of 15°) than the modified GDx that we used. Both changes result in a 2.67 times lower sampling density. This lower sampling density is unlikely to cause any problems for the detection of the edges, as long as the wedge is wide enough to prevent one edge interfering detection of the other edge. Wedge defects are, by definition, larger than the diameter of large veins,24 which are still at least a few pixels wide on the GDx VCC. On the other hand, the larger viewing angle of the GDx VCC may further improve the performance since the masking of wedge defects by blood vessels decreases farther from the optic disc. Although some changes to the algorithm may be necessary, such as a different transformation due to the deflection from the radial direction of the NFL bundles increasing with the distance from the optic disc, we expect it to perform better in automatically detecting wedge defects in images acquired with the GDx VCC. Further research is required to test and fine-tune our algorithm to GDx VCC images.

In conclusion, with a sensitivity of 55% at a specificity of 95%, our automated method may be very useful for detecting wedge defects in scanning laser polarimetric images. The visibility of wedge defects as well as the performance of our algorithm is best when there is no or only little diffuse NFL loss. With mainly localized loss, the standard parameters of the GDx are likely to fail to detect the presence of glaucoma. For advanced glaucoma, with moderate to severe diffuse loss, the diagnostic accuracy of the GDx is high7, 25, 26 and additional testing for wedges is probably not deeded for making a right diagnosis. Consequently, our algorithm adds to current classification methods of the GDx.