Abstract
For genotype data being sampled from several strata with different allele frequencies, it is necessary to verify the assumption of homogeneity of Hardy–Weinberg disequilibrium across strata before testing Hardy–Weinberg law across strata. In practice, disequilibrium can be measured via fixation coefficients (ie, ratios of genotypic frequencies) or disequilibrium coefficients (ie, differences of genotypic frequencies). Test for homogeneity of Hardy–Weinberg disequilibrium using data from several populations has been derived according to fixation coefficients. In this article, using the likelihood score theory extended to nuisance parameters, we derive a homogeneity score test for comparing disequilibrium coefficients across several independent strata. Simulation results demonstrate that the homogeneity score test performs satisfactorily in the sense that its empirical size seldom exceeds the pre-chosen nominal level by more than 10% even for small sample sizes. Corresponding power and sample size formulae are provided as well. We illustrate our test with a real glyoxalase genotype data set.
Similar content being viewed by others
Introduction
The law of Hardy–Weinberg equilibrium (HWE) states that in a large random mating population that is not affected by the evolutionary processes of mutation, migration, or selection, both the allele frequencies and the genotype frequencies are constant from generation to generation.1, 2 Furthermore, the genotype frequencies are related to the allele frequencies by the square expansion of those allele frequencies. In other words, the law of HWE states that under a restrictive set of assumptions, it is possible to calculate the expected frequencies of genotypes in a population if the frequency of the different alleles in a population is known. The original descriptions of HWE become an important landmark in the history of population genetics,3 and it is now a common practice to verify whether observed genotypes conform to Hardy–Weinberg expectations.4, 5
In a diallelic locus with alleles A1 and A2 across K strata, let the genotypic array of the kth (k=1, …, K) stratum be

Let pk be the allelic frequency of A1 in the kth stratum and qk=1−pk (k=1, …, K). Populations with genotypic frequencies satisfying p11k=pk2, p12k=2pkqk, and p22k=qk2 (k=1, …, K) are said to be in HWE at the locus under consideration. In studies of HWE, there are two widely used coefficients, namely the fixation and disequilibrium coefficients.6 For stratum k (k=1, …, K), the fixation and disequilibrium coefficients are defined by  and Dk=pkqk−p12k/2, respectively. Hence, the problem of testing HWE when individuals are sampled from several strata is equivalent to testing one of the following hypotheses:
and Dk=pkqk−p12k/2, respectively. Hence, the problem of testing HWE when individuals are sampled from several strata is equivalent to testing one of the following hypotheses:

where θk=fk or Dk. For statistical tests based on disequilibrium coefficient, one can refer to the work of Haldane7 and Smith.8 For test procedures based on functions of fixation coefficients (eg, (1−fk)2), one can consult the work of Emigh,9 Troendle and Yu,10 and Nam.11
It is noteworthy that any statistical procedure for testing the null hypothesis in (1) assumes that the measure of disequilibrium (ie, θk) is constant across the strata. In this regard, it is important that one should consider testing the assumption of homogeneity of the measure of disequilibrium across strata before any testing of the null hypothesis in (1). For this purpose, we consider the following hypotheses:

Olson and Foley12 proposed a large-sample test and an exact test for verifying the null hypothesis H0 via a function of fixation coefficients, (1−fk)2. They also approximate the P-value of the exact test using a Markov chain Monte Carlo approach. Although the use of fixation coefficients to describe departures from HWE has some merit, it has the disadvantage that these parameters are estimated as ratios of genotypic frequencies. It is difficult to study sampling properties of ratio statistics.4, 6 Besides, functions of fixation coefficients such as (1−fk)2 may possess infinite upper bound. On the other hand, there are advantages in working with a composite kind of quantity such as the disequilibrium coefficient. This is simply the difference between a frequency and its values expected when there are no association between alleles. Moreover, it is easy to show that disequilibrium coefficient Dk satisfies max{−pk2, −qk2}⩽Dk⩽pkqk. Unfortunately, test of homogeneity of disequilibrium coefficients across several strata has not been considered in the literature yet. Therefore, the objective of this study is to develop a new homogeneity score statistic for testing the null hypothesis in (2) based on disequilibrium coefficients. We first develop the theory and method and then demonstrate the advantage of our method over the method proposed by Olson and Foley12 via Monte Carlo simulation studies. We also derive the approximate power and sample size formulae, which are necessary in design of studies. Finally, we illustrate our test with a real glyoxalase genotype data set.
Method
Homogeneity test
Let Xijk (i⩽j=1, 2 and k=1, …, K) be the number of individuals with genotype AiAj in the kth population with nk=X11k+X12k+X22k. Let M(nk, {pijk}) denote the trinomial distribution with parameter vector (p11k, p12k, p22k). Hence, we have {Xijk: i, j=1, 2; i⩽j}∼M(nk, {pijk}) for k=1, …, K. In this article, we are interested to test the homogeneity hypothesis in (2) with θk=Dk. That is,

where Dk=pkqk−p12k/2. All subsequent results are obtained under the assumptions that K is fixed and nk is sufficiently large for k=1, 2, …, K.
Note that p11k=pk2+Dk, p12k=2(pkqk−Dk) and p22k=qk2+Dk, the log-likelihood for the kth strata can be expressed in terms of Dk and pk (k=1, …, K) as

Let D denote the common disequilibrium coefficient under H0 and p=(p1, …, pK)′ the nuisance parameter vector. Under H0, the total log-likelihood for all K strata is given by

Hence, the efficient scores for the kth stratum (ie, the first-order derivatives of lk(D,pk) with respect to D and pk) are given by

Let D̂ and p̂ be the maximum-likelihood estimates (MLEs) of D and p under the null hypothesis H0. In this case, D̂ and p̂ must satisfy the following K+1 equations:

Denote

In addition, denote  , where
, where

Hence, the likelihood score test for testing H0: D1=⋯=DK is given by

which is asymptotically distributed as a χ2 variate with K−1 degrees of freedom under H0. Unfortunately, we note that D̂ and p̂ cannot be expressed in closed form and this makes the likelihood score test X2 less appealing in real applications. To over this issue, using the theory of homogeneity score test extended to nuisance parameters,13 we consider the following modified score statistic:

where D* and p* are any consistent estimators of D and p, respectively. To this end, we choose D* to be  and p*k be the solution to the following equation:
and p*k be the solution to the following equation:

or equivalently the following quintic polynomial equation,

where a0=x12kD*(1+D*)+2x22k(D*)2, a1=−2(nkD* (1+D*)+x12kD*), a2=6nkD*+2x11k+x12k, a3=−2(2nkD*+ nk+2x11k+x12k), a4=4nk+2x11k+x12k, and a5=−2nk. Here, D* is analogous to the Mantel–Haenszel estimator14 and is a consistent estimator to D. However, it is not an efficient estimator to D in general. The proof of consistency and the condition to attain asymptotic efficiency for D* is given in Appendix A. We note that the calculation of  in (3) could be tedious. Nonetheless, it is easy to show that
in (3) could be tedious. Nonetheless, it is easy to show that  is simply given by nk/wk(D, pk) with wk(D, pk)=(pk2+D) (qk2+D)2+2(pkqk−D)3+(pk2+D)2(qk2+D)−4D2 (see Appendix B for the proof). Similarly, X2* is asymptotically distributed as a χ2 variate with K−1 degrees of freedom under H0. Therefore, the homogeneity hypothesis H0 is rejected at level α if X2*⩾χK−1,(1−α)2, where χK−1,(1−α)2, is the 100 × (1−α) percentile point of the χ2 distribution with K−1 degrees of freedom. Finally, it is noteworthy that if the consistent estimators of D and p are the constrained maximum-likelihood estimators under H0, then the second term of (3) vanishes, since ∑k=1K HkD(D*, pk*)=0, and (3) reduces to the likelihood score statistic.
is simply given by nk/wk(D, pk) with wk(D, pk)=(pk2+D) (qk2+D)2+2(pkqk−D)3+(pk2+D)2(qk2+D)−4D2 (see Appendix B for the proof). Similarly, X2* is asymptotically distributed as a χ2 variate with K−1 degrees of freedom under H0. Therefore, the homogeneity hypothesis H0 is rejected at level α if X2*⩾χK−1,(1−α)2, where χK−1,(1−α)2, is the 100 × (1−α) percentile point of the χ2 distribution with K−1 degrees of freedom. Finally, it is noteworthy that if the consistent estimators of D and p are the constrained maximum-likelihood estimators under H0, then the second term of (3) vanishes, since ∑k=1K HkD(D*, pk*)=0, and (3) reduces to the likelihood score statistic.
Asymptotic power and sample size formulae
In this section, we aim to derive the asymptotic power and sample size formulae15 based on X2*. For these purposes, we assume nk=nbk for some n and bk>0. Let D̄k and p̄k be the true parameter values for Dk and pk under the alternative H1, where k=1, 2, …, K and D̄k≠D̄j for some k≠j. Hence, the asymptotic power of the homogeneity score test X2* at α level is given by

where χK−12 (δ) denotes the non-central χ2 distribution with K–1 degrees of freedom and the non-centrality parameter δ is equal to

with q̄k=1−p̄k,

and pk is the solution to the following equation:

where ā0=2(p̄kq̄k−D̄k)D(1+D)+2(q̄k2+D̄k)D2, ā1=−2D(1+D)+4(p̄kq̄k−D̄k)D, ā2=6D+2p̄k, ā3=−2(2D+1+p̄k), ā4=4+p̄k, and ā5=−2.
As a result, the desirable sample size n required to attain the power at 1−β with D̄k and p̄k being the true parameter values for Dk and pk under the alternative H1 at nominal level α can be determined from the following equality:

where χK−1,β2 (δ) is the 100 × β percentage point of the non-central χ2 distribution with K−1 degrees of freedom with non-centrality parameter being δ. The value of n can be readily obtained by solving the equation given in (4).
Simulation
We evaluate the performance of our proposed homogeneity score test in terms of type I error rate and power. For type I error rate, we include the homogeneity test proposed by Olson and Foley12 in our comparison study. In their case, they adopted a function of fixation coefficients as the measure for Hardy–Weinberg disequilibrium. Specifically, they were interested to test the homogeneity hypothesis in (2) with θk=(1−fk)2. That is,
H0*: (1−f1)2=⋯=(1−fK)2 versus H1*: Not all (1−fk)2 are equal, and their proposed statistic for testing the above hypotheses is given by

where θ̂=(∑k=1K((x12k2−x12k)/(2(2nk−1)))/(∑k=1K((2x11k2− x22k)/(2nk−1))), hk(θ)=x12k2−x12k−4θx11kx22k, and Vâr [hk(θ)]= 4(x11k3−3x11k2+2x11k)(1−θ)+2(x11k2−x11k) (2nkθ−3θ +2) for k=1, …, K. We would like to point out here that our proposed homogeneity score test (ie, X2*) and Olson and Foley's test (ie, Thomog2) can be fairly comparable only when θk=0 for k=1, …, K in the null hypotheses H0 and H0* (ie, H′0 in (1)). In the present comparisons, we consider both the asymptotic (denoted as Thomog,a2) and exact (denoted as Thomog,e) versions of Thomog2. For the implementation of Thomog,e2, one can refer to Olson and Foley (1996, p 975). Here, we investigate type I error rates of X2* and Thomog,a for small (eg, nk=20 and 30) to large sample sizes (eg, nk=50–200) when θk=0 for k=1, …, K. As Thomog,e2 is computationally intensive for large sample sizes, we consider its small-sample behavior only. Results of Monte Carlo experiments with 5 000 repetitions for different designed allele probabilities p′ks with k=1, …, K and K=3 and 5 at 0.05 nominal level are summarized in Tables 1 (for small sample sizes) and 2 (for moderate to large sample sizes).
As expected, the exact test T2homog,e is always conservative (ie, its type I error rates are always less than the pre-assigned nominal level). The empirical type I error rates of our asymptotic homogeneity score test X2* are satisfactorily close to the nominal 0.05 level for allelic probabilities being bounded away from 0 and 1, whereas those of the Thomog,a2 are generally liberal (eg, more than 11 times of the given nominal level) even for large sample sizes. It is noteworthy that X2* appears to be conservative than Thomog,e2, for small allele probabilities (eg, pk's being 0.1). However, the conservativeness of X2* vanishes with an increase in sample sizes and the computation of X2* is much more simpler than Thomog,e2.
In view of the above observations, we prefer the proposed homogeneity score test X2* (based on disequilibrium coefficients) to the existing homogeneity tests based on function of fixation coefficients (ie, Thomog,a2, and Thomog,e2). Hence, we exclude Thomog,a2, and Thomog,e2 in all subsequent evaluation and discussion. Table 3 further summarizes the type I error rate of X2* for some non-zero (common) disequilibrium coefficients (ie, D≠0) under different settings. Again, the propose homogeneity score test performs satisfactorily in the sense that its empirical type I error rates are close to the pre-chosen nominal level and seldom exceed the nominal level by more than 10%.
For power performance, the parameters and sample size are quite similar to those adopted in Table 3, except that {Dk} are now specifically designed under H1. For this purpose, we set Dk=D0+Δ(k−1). For K=3, we consider: (i) D0=−0.03, Δ=0.03 and (ii) D0=−0.05, Δ=0.05. For K=5, we consider: (i) D0=−0.06, Δ=0.03 and (ii) D0=−0.1, Δ=0.05. The results are reported in Table 4. From the simulation results, the power of X2* increases with the sample size n or Δ. For those settings with the same {Dk}, the one with varied allele probabilities across strata usually have power greater than that with equal allele probabilities across strata.
Real example
Ghosh reported genotype frequencies of red cell glyoxalase 1 (GLO) polymorphism from several populations.16 We consider the data, reproduced in Table 5, from four populations in the Western Pacific Area. The gene frequencies of four populations highly vary from 0.0455 in the Eastern Carolines to 0.3611 in the Tokelau Islands, Samoa and Fuji in between. The estimated disequilibrium coefficients (ie, D̂k) in the four populations are ranging from 0.0145–0.019, which are close to zero. This seems to suggest that the homogeneity of HWE across the four populations, although the gene frequencies vary appreciably. Our proposed homogeneity score test yields X2*=2.33 with P-value being 0.51. Hence, it is now safe to assume that the HWE is simultaneously valid across the four populations. We apply the Olson and Foley's test to the same glyoxalase genotype data set in the Western Pacific Area. Function of fixation coefficients (ie, (1−fK)2) was adopted and the corresponding homogeneity test yields Thomog,a2=2.78 with P-value being 0.43. In this case, both tests reach the same conclusion.
Discussion
In practice, one is tempted to test the Hardy–Weinberg law across several independent populations without verifying the underlying assumption of homogeneity of Hardy–Weinberg disequilibrium across populations. Verification of the latter assumption is critical in genotype data analysis. Olson and Foley proposed a homogeneity test for this purpose. Unfortunately, our simulations show that their asymptotic version test is not reliable (ie, inflated type I error rates) even in large sample size. Although an exact version test was also proposed to overcome the liberty issue, such a test is however always conservativeness and computationally intensive for large sample sizes.
In this paper, we consider a homogeneity score test based on disequilibrium coefficients. Empirical results from our simulation studies support that our homogeneity score test is a reliable asymptotic testing procedure even for small sample sizes. However, our test may suffer the drawback that it may be quite conservative for rare allelic probabilities (eg, ⩽0.1). In this case, one may require larger sample sizes to overcome the conservativeness issue. In this regard, we also provide a sample size formula for design purpose. We have implemented the test procedures described in this manuscript in a Matlab program, which can be downloaded from the web site: http://math.nenu.edu.cn/jhguo/program.htm.
We also applied the Kolmogorov–Smirnov test to study the asymptotic behaviors of our test (ie, X2*). Briefly, for allele frequency greater than or equal to 0.1, we find that the asymptotic χ2 sampling distribution property follows for moderate sample sizes (eg, nk⩾50). For rare allele frequency (ie, <0.1), larger sample sizes are required. In fact, after some straightforward algebra, we observe that HkD (D*, pk*) has larger variance for rare pk. This may explain the severe conservativeness of X2* for rare pk. We are now undertaking an investigation of possible modification of X2* for conservative correction.
We note that exact (conditional) method works in Olson and Foley12 as they considered fixation coefficient f's which in turn are odds ratio. In their case, sufficient statistics for those nuisance parameters exist and can be eliminated by conditioning on their sufficient statistics. On the contrary, we consider the disequilibrium coefficient D's, which are actually rate differences. In our case, sufficient statistics do not exist for the corresponding nuisance parameters and the exact conditional method hence is not applicable.17
Finally, the theories developed in this paper can be readily extended to genotype data with multiple alleles.
References
Hardy GH : Mendelian proportions in a mixed population. Science 1908; 28: 49–50.
Weinberg W : Papers on Human Genetics. Englewood Cliffs, NJ: Prentice-Hall, 1908, In (translation by Boyer SH) On the Demonstration of Heredity in Man 1963.
Crow JE : Eighty years ago: the beginnings of population genetics. Genetics 1988; 119: 473–476.
Hernandez JL, Weir BS : A disequilibrium coefficient approach to Hardy–Weinberg testing. Biometrics 1989; 45: 53–70.
Olson JM : Testing the Hardy–Weinberg law across strata. Ann Hum Genet 1993; 57: 291–295.
Weir BS : Genetic Data Analysis II. Sunderland, MA: Sinauer Associates, Inc., 1996, pp 91–140.
Haldane JBS : An exact test for randomness of mating. J Genet 1954; 52: 631–635.
Smith CAB : A note on testing the Hardy–Weinberg law across strata. Ann Hum Genet 1970; 33: 377–383.
Emigh TH : A comparison of tests for Hardy–Weinberg equilibrium. Biometrics 1980; 36: 627–642.
Troendle JJ, Yu KF : A note on testing the Hardy–Weinberg law across strata. Ann Hum Genet 1994; 58: 397–402.
Nam JM : Testing a genetic equilibrium across strata. Ann Hum Genet 1997; 61: 163–170.
Olson JM, Foley M : Testing for homogeneity of Hardy–Weinberg disequilibrium using data sampled from several populations. Biometrics 1996; 52: 971–979.
Tarone RE : Homogeneity score tests with nuisance parameters. Commun Statist Theory Meth 1988; 17: 1549–1556.
Mantel N, Haenszel W : Statistical aspects of the analysis of data from retrospective studies of disease. J Natl Cancer Inst 1959; 22: 719–748.
Guo JH, Ma YP, Shi NZ, Lau TS : Testing for homogeneity of relative difference under inverse sampling. Comput Statist Data Anal 2004; 44: 613–624.
Ghosh AK : Polymorphism of red cell glyoxalase 1 with special reference to South and Southeast Asian and Oceania. Hum Genet 1977; 39: 91–95.
Agresti A : Exact inference for categorical data: recent advances and continuing controversies. Statist Med 2001; 20: 2709–2722.
Acknowledgements
This research is supported by the NSFC (Grant Numbers 10431010, 10329102, and 10371015), the Science and Technology Keystone Fund of MOE, P.R. China (Grant Numbers 104070 and 00041), NCET-04-0310, EYTP, the Jilin Distinguished Young Scholars Program (Grant Number 20030113), and the Science Foundation for Young Teachers of NENU (Grant Number 20060101). The work of ML Tang was fully supported by a grant from the Research Grant Council of the Hong Kong Special Administration (Project Number CUHK4371/04 M) and Hong Kong Baptist University Grants FRG/04-05/II-01 and FRG/04-05/II-20.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
Consistency and the condition to attain asymptotic efficiency for D*
Let nk=nbk, with bk>0 and k=1, 2, …, K. The asymptotic property of D* is obtained under the assumption that K is fixed and n approaches infinity (ie, sufficiently large). Following the notation above, the Mantel–Haenszel-type estimator of D* can be rewritten as

By the Central Limit Theorem,  has an asymptotic normal distribution, N(0,∑k/bk). By delta method, we obtain
has an asymptotic normal distribution, N(0,∑k/bk). By delta method, we obtain  has an asymptotic normal distribution with mean 0 and variance wk(Dk,pk)/bk. As Dk=D under H0 for k=1, 2, …, K, we can derive that D* is a consistent estimate of D. Let wk=wk(D,pk), vk=1/(pkqk−D). Hence, the asymptotic variance of D* under H0 is given by
has an asymptotic normal distribution with mean 0 and variance wk(Dk,pk)/bk. As Dk=D under H0 for k=1, 2, …, K, we can derive that D* is a consistent estimate of D. Let wk=wk(D,pk), vk=1/(pkqk−D). Hence, the asymptotic variance of D* under H0 is given by

Denote the information matrix with respect to D and p under H0 by

By inverting I, we can obtain the asymptotic variance of D̂, which is given by

By the Cauchy–Schwarz inequality

Thus, AsyVar(D̂)⩽AsyVar(D*) and we get the sufficient and necessary condition for the asymptotic efficiency of D*, that is, wkvk2=c, k=1, 2, …, K, where c is a constant independent of all the parameters. The condition is satisfied if D=0. From the above discussion, we know that D* is inefficient in general case.
Appendix B
Simple expression for 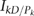
For the kth stratum, we denote the information matrix with respect to Dk and pk by

By the property of inverse matrix, IkD/pk(Dk,pk) is equal to the reciprocal of the (1,1) element of Ik−1. On the one hand, according to the property of MLEs, we have

where D̂k=(4x11kx22k−x12k2)/(4nk2) is the MLE of Dk. Therefore, the asymptotic variance of  is
is  . On the other hand, let yk=(x11k, x12k, x22k)/nk, by the Central Limit Theorem,
. On the other hand, let yk=(x11k, x12k, x22k)/nk, by the Central Limit Theorem,  has an asymptotic normal distribution, N(0, ∑k), where gk=(p11k, p12k, p22k)′, ∑k=diag(gk)−gkg′k. Let
has an asymptotic normal distribution, N(0, ∑k), where gk=(p11k, p12k, p22k)′, ∑k=diag(gk)−gkg′k. Let  . By delta method, we obtain
. By delta method, we obtain  has an asymptotic normal distribution with mean 0 and variance c′k∑kck. After simple calculation, we have c′k∑kck=wk(Dk,pk). Hence, we can give the exact expression
has an asymptotic normal distribution with mean 0 and variance c′k∑kck. After simple calculation, we have c′k∑kck=wk(Dk,pk). Hence, we can give the exact expression  . Naturally, the expression of
. Naturally, the expression of  is just
is just  by substituting D for Dk.
by substituting D for Dk.
Rights and permissions
About this article
Cite this article
Yin, XL., Ma, WQ., Tang, ML. et al. A test of homogeneity of Hardy-Weinberg disequilibrium across strata. Eur J Hum Genet 14, 1223–1230 (2006). https://doi.org/10.1038/sj.ejhg.5201689
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/sj.ejhg.5201689