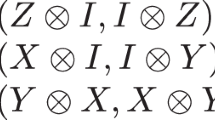Abstract
Algorithms such as quantum factoring1 and quantum search2 illustrate the great theoretical promise of quantum computers; but the practical implementation of such devices will require careful consideration of the minimum resource requirements, together with the development of procedures to overcome inevitable residual imperfections in physical systems3,4,5. Many designs have been proposed, but none allow a large quantum computer to be built in the near future6. Moreover, the known protocols for constructing reliable quantum computers from unreliable components can be complicated, often requiring many operations to produce a desired transformation3,4,5,7,8. Here we show how a single technique—a generalization of quantum teleportation9—reduces resource requirements for quantum computers and unifies known protocols for fault-tolerant quantum computation. We show that single quantum bit (qubit) operations, Bell-basis measurements and certain entangled quantum states such as Greenberger–Horne–Zeilinger (GHZ) states10—all of which are within the reach of current technology—are sufficient to construct a universal quantum computer. We also present systematic constructions for an infinite class of reliable quantum gates that make the design of fault-tolerant quantum computers much more straightforward and methodical.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Shor,P. in Proc. 35th Annu. Symp. on Foundations of Computer Science (ed. Goldwasser, S.) 124–134 (IEEE Computer Society Press, Los Alomitos, 1994).
Grover,L. K. Quantum computers can search arbitrarily large databases by a single query. Phys. Rev. Lett. 79, 4709–4012 (1997).
Preskill,J. Reliable quantum computers. Proc. R. Soc. Lond. A 454, 385–410 (1998).
Steane,A. M. Efficient fault tolerant quantum computing. Nature 399, 124–126 (1999).
Gottesman,D. Theory of fault-tolerant quantum computation. Phys. Rev. A 57, 127–137 (1998).
Preskill,J. Quantum computing: pro and con. Proc. R. Soc. Lond. A 454, 469–486 (1998).
Shor,P. W. in Proc. 37th Annu. Symp. on Foundations of Computer Science (IEEE Computer Society Press, Los Alamitos, 1996).
Knill,E., Laflamme,R. & Zurek,W. Resilient quantum computation. Science 279, 342–345 (1998).
Bennett,C. H. et al. Teleporting an unknown quantum state via dual classical and EPR channels. Phys. Rev. Lett. 70, 1895–1899 (1993).
Greenberger,D., Horne,M., Shimony,A. & Zeilinger,A. Bell's theorem without inequalities. Am. J. Phys. 58, 1131–1143 (1990).
Brassard,G. in PhysComp 96 (eds Toffoli, T., Biafore, M. & Leao, J.) 48–50 (New England Complex Systems Inst., Cambridge, Massachusetts, 1996).
Gottesman,D. in Group22: Proc. XXII Int. Colloquium on Group Theoretical Methods in Physics (eds Corney, S. P., Delbourgo, R. & Jarvis, P. D.) 32–43 (International Press, Cambridge, Massachusetts, 1999).
Nielsen,M. A. & Chuang,I. L. Programmable quantum gate arrays. Phys. Rev. Lett. 79, 321–324 (1997).
Barenco,A. et al. Elementary gates for quantum computation. Phys. Rev. A 52, 3457–3467 (1995).
Calderbank,A. R., Rains,E. M., Shor,P. W. & Sloane,N. J. A. Quantum error correction and orthogonal geometry. Phys. Rev. Lett. 78, 405–408 (1997).
Steane,A. M. Multiple particle interference and quantum error correction. Proc. R. Soc. Lond. A 452, 2551–2576 (1996).
Steane,A. M. Error correcting codes in quantum theory. Phys. Rev. Lett. 77, 793–797 (1996).
Gottesman,D. Stabilizer Codes and Quantum Error Correction. Thesis, California Inst. of Technol. (1997).
Boykin,P. O., More,T., Pulver,M., Roychowdhury,V. & Vatan,F. On universal and fault-tolerant quantum computing. Preprint quant-ph/9906054 (cited June 1999) at 〈http://xxx.lanl.gov〉 (1999).
Kwiat,P. G. & Weinfurter,H. Embedded Bell-state analysis. Phys. Rev. A 58, R2623–R2626 (1998).
Bouwmeester,D. et al. Experimental quantum teleportation. Nature 390, 575–579 (1997).
Bouwmeester,D. et al. Observation of three-photon Greenberger-Horne-Zeilinger entanglement. Phys. Rev. Lett. 82, 1345–1349 (1999).
Chuang,I. L. & Yamamoto,Y. Simple quantum computer. Phys. Rev. A 52, 3489–3496 (1995).
Acknowledgements
We thank C. Bennett for suggesting the concept of “quantum sofrware” to us, and R. Jozsa for pointing out an error in an early version of this manuscript. We also thank J. Kempe, D. Leung, and D. Bacon for helpful discussions. This work was supported in part by DARPA under the NMRQC initiative.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gottesman, D., Chuang, I. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 402, 390–393 (1999). https://doi.org/10.1038/46503
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/46503
This article is cited by
-
Time-Efficient Constant-Space-Overhead Fault-Tolerant Quantum Computation
Nature Physics (2024)
-
Routing in quantum communication networks using reinforcement machine learning
Quantum Information Processing (2024)
-
Scalable quantum processors empowered by the Fermi scattering of Rydberg electrons
Communications Physics (2023)
-
Approximate symmetries and quantum error correction
npj Quantum Information (2023)
-
Deterministic Bell state measurement with a single quantum memory
npj Quantum Information (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.