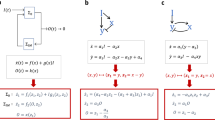
Abstract
Cells use complex networks of interacting molecular components to transfer and process information. These “computational devices of living cells”1 are responsible for many important cellular processes, including cell-cycle regulation and signal transduction. Here we address the issue of the sensitivity of the networks to variations in their biochemical parameters. We propose a mechanism for robust adaptation in simple signal transduction networks. We show that this mechanism applies in particular to bacterial chemotaxis2,3,4,5,6,7. This is demonstrated within a quantitative model which explains, in a unified way, many aspects of chemotaxis, including proper responses to chemical gradients8,9,10,11,12. The adaptation property10,13,14,15,16 is a consequence of the network's connectivity and does not require the ‘fine-tuning’ of parameters. We argue that the key properties of biochemical networks should be robust in order to ensure their proper functioning.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Bray, D. Protein molecules as computational elements in living cells. Nature 376, 307–312 (1995).
Stock, J. B. & Surette, M. in E. coli and S. typhimurium: Cellular and Molecular Biology (ed. Neidhardt, F. C.) 1103–1129 (American Soceity of Microbiology, Washington DC, (1996)).
Parkinson, J. S. Signal transduction schemes of bacteria. Cell 73, 857–871 (1993).
Hazelbauer, G. L., Berg, H. C. & Matsumura, P. M. Bacterial motility and signal transduction. Cell 73, 15–22 (1993).
Bourret, R. B., Borkovich, K. A. & Simon, M. I. Signal transduction pathways involving protein phosphorylation in prokaryotes. Annu. Rev. Biochem. 60, 401–441 (1991).
Adler, J. Chemotaxis in bacteria. Annu. Rev. Biochem. 44, 341–356 (1975).
Bray, D., Bourret, R. B. & Simon, M. I. Computer simulation of the phosphorylation cascade controlling bacterial chemotaxis. Mol. Biol. Cell 4, 469–482 (1993).
Adler, J. Chemotaxis in bacteria. Science 153, 708–716 (1996).
Berg, H. C. & Brown, D. A. Chemotaxis in E. coli analysed by three-dimensional tracking. Nature 239, 500–504 (1972).
Macnab, R. M. & Koshland, D. E. The gradient-sensing mechanism in bacterial chemotaxis. Proc. Natl Acad. Sci. USA 69, 2509–2512 (1972).
Block, S. M., Segall, J. E. & Berg, H. C. Impulse responses in bacterial chemotaxis. Cell 31, 215–226 (1982).
Koshland, D. E. Aresponse regulator model in a simple sensory system. Science 196, 1055 (1977).
Berg, H. C. & Tedesco, P. M. Transient response to chemotactic stimuli in E. coli. Proc. Natl Acad. Sci. USA 72, 3235–3239 ((1975)).
Springer, M. S., Goy, M. F. & Adler, J. Protein methylation in behavioural control mechanism and in signal transduction. Nature 280, 279–284 (1979).
Koshland, D. E., Goldbeter, A. & Stock, J. B. Amplification and adaptation in regulatory and sensory systems. Science 217, 220–225 (1982).
Khan, S., Spudich, J. L., McCray, J. A. & Tentham, D. R. Chemotactic signal integration in bacteria. Proc. Natl Acad. Sci. USA 92, 9757–9761 (1995).
Segel, L. A., Goldbeter, A., Devreotes, P. N. & Knox, B. E. Amechanism for exact sensory adaptation based on receptor modification. J. Theor. Biol. 120, 151–179 (1986).
Hauri, D. C. & Ross, J. Amodel of excitation and adaptation in bacterial chemotaxis. Biophys. J. 68, 708–722 (1995).
Asakura, S. & Honda, H. Two-state model for bacterial chemoreceptor proteins. J. Mol. Biol. 176, 349–367 (1984).
Spudich, J. L. & Koshland, D. E. Non-genetic individuality: chance in the single cell. Nature 262, 467–471 (1976).
Kleene, S. J., Hobson, A. C. & Adler, J. Attractants and repellents influence methylation and demethylation of methyl-accepting proteins in an extract of E. coli. Proc. Natl Acad. Sci. USA 76, 6309–6313 (1979).
Acknowledgements
We thank J. Stock, M. Surette, A. C. Maggs, U. Alon, L. Hartwell, M. Kirschner, A.Levine, A. Libchaber, A. Murray and T. Surrey for discussion; A. C. Maggs for help with numerical issues; and J. Stock, M. Surette and H. Berg for introducing us to bacterial chemotaxis and pointing out many useful references. This work has been partially supported by grants from the NIH and the NSF. N.B. is a Rothschild Fellow and a Dicke Fellow at Princeton University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Barkai, N., Leibler, S. Robustness in simple biochemical networks. Nature 387, 913–917 (1997). https://doi.org/10.1038/43199
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/43199
This article is cited by
-
Ideal adaptive control in biological systems: an analysis of \(\mathbb {P}\)-invariance and dynamical compensation properties
BMC Bioinformatics (2024)
-
Role of ultrasensitivity in biomolecular circuitry for achieving homeostasis
Nonlinear Dynamics (2024)
-
Optogenetic control of YAP reveals a dynamic communication code for stem cell fate and proliferation
Nature Communications (2023)
-
A blueprint for a synthetic genetic feedback optimizer
Nature Communications (2023)
-
Universal structures for adaptation in biochemical reaction networks
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.