Abstract
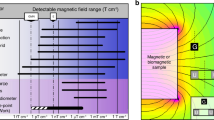
Magnetic fields change the way that electrons move through solids. The nature of these changes reveals information about the electronic structure of a material and, in auspicious circumstances, can be harnessed for applications. The silver chalcogenides, Ag2Se and Ag2Te, are non-magnetic materials, but their electrical resistance can be made very sensitive to magnetic field by adding small amounts—just 1 part in 10,000—of excess silver1,2,3,4. Here we show that the resistance of Ag2Se displays a large, nearly linear increase with applied magnetic field without saturation to the highest fields available, 600,000 gauss, more than a million times the Earth's magnetic field. These characteristics of large (thousands of per cent) and near-linear response over a large field range make the silver chalcogenides attractive as magnetic-field sensors, especially in physically tiny megagauss (106 G) pulsed magnets where large fields have been produced but accurate calibration has proved elusive. High-field studies at low temperatures reveal both oscillations in the magnetoresistance and a universal scaling form that point to a quantum origin5,6 for this material's unprecedented behaviour.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Xu, R. et al. Large magnetoresistance in non-magnetic silver chalcogenides. Nature 390, 57–60 (1997)
Chuprakov, I. S. & Dahmen, K. H. Large positive magnetoresistance in thin films of silver telluride. Appl. Phys. Lett. 72, 2165–2167 (1998)
Ogorelec, Z., Hamzic, A. & Basletic, M. On the optimization of the large magnetoresistance of Ag2Se. Europhys. Lett. 46, 56–61 (1999)
Schnyders, H. S., Saboungi, M.-L. & Rosenbaum, T. F. Magnetoresistance in n- and p-type Ag2Te: Mechanisms and applications. Appl. Phys. Lett. 76, 1710–1712 (2000)
Abrikosov, A. Quantum magnetoresistance. Phys. Rev. B 58, 2788–2794 (1998)
Abrikosov, A. Quantum linear magnetoresistance. Europhys. Lett. 49, 789–793 (2000)
Boebinger, G. S., Lacerda, A. H., Schneider-Muntau, H. J. & Sullivan, N. The National High Magnetic Field Laboratory's pulsed magnetic field facility in Los Alamos. Physica B 294–295, 512–518 (2001)
Mackay, K., Bonfim, M., Givord, D. & Fontaine, A. 50 T pulsed magnetic fields in microcoils. J. Appl. Phys. 87, 1996–2002 (2000)
von Ortenberg, M. et al. The Humboldt high magnetic field center at Berlin. Physica B 294–295, 568–573 (2001)
Drndic, M., Johnson, K. S., Thywissen, J. H., Prentiss, M. & Westervelt, R. M. Micro-electromagnets for atom manipulation. Appl. Phys. Lett. 72, 2906–2908 (1998)
Kohler, M. Zur magnetischen Widerstandsänderung reiner Metalle. Ann. Phys. 32, 211–218 (1938)
Pippard, A. P. Magnetoresistance in Metals (Cambridge Univ. Press, Cambridge, 1989)
McKenzie, R. H., Qualls, J. S., Han, S. Y. & Brooks, J. S. Violation of Kohler's rule by the magnetoresistance of a quasi-two-dimensional organic metal. Phys. Rev. B 57, 11854–11857 (1998)
Harris, J. M. et al. Violation of Kohler's rule in the normal state magnetoresistance of YBa2Cu3O7-δ and La2 - xSrxCuO4 . Phys. Rev. Lett. 75, 1391–1394 (1995)
Herring, C. Effect of random inhomogeneities on electrical and galvanomagnetic measurements. J. Appl. Phys. 31, 1939–1953 (1960)
Aliev, S. A. & Aliev, F. F. Band parameters and energy structure of β-Ag2Se. Izv. Akad. Nauk SSSR Neorg. Mater. 21, 1869–1872 (1985)
Tritton, D. J. Physical Fluid Dynamics (Van Nostrand Reinhold, New York, 1977)
Acknowledgements
We thank H. Hwang, L. P. Kadanoff and H. S. Schnyders for discussions, and the late R. Xu for technical assistance. The work at the University of Chicago and at Argonne National Laboratory was supported by DOE Basic Energy Sciences.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Rights and permissions
About this article
Cite this article
Husmann, A., Betts, J., Boebinger, G. et al. Megagauss sensors. Nature 417, 421–424 (2002). https://doi.org/10.1038/417421a
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/417421a
This article is cited by
-
Anisotropic positive linear and sub-linear magnetoresistivity in the cubic type-II Dirac metal Pd3In7
npj Quantum Materials (2023)
-
Giant Magnetoresistance Effect in the Square Networks with Regular Impurities
Journal of Superconductivity and Novel Magnetism (2023)
-
Polyethyleneimine–Chromium Oxide Nanocomposite Sensor with Patterned Copper Clad as a Substrate for CO2 Detection
Journal of Electronic Materials (2022)
-
Topologically driven linear magnetoresistance in helimagnetic FeP
npj Quantum Materials (2021)
-
Exchange bias and large room temperature magnetoresistance in ion beam-synthesized Co nanoparticles in SiO2
Emergent Materials (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.