Abstract
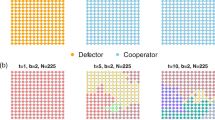
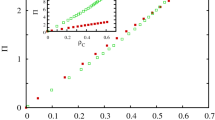
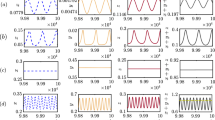
MUCH attention has been given to the Prisoners' Dilemma as a metaphor for the problems surrounding the evolution of coopera-tive behaviour1–6. This work has dealt with the relative merits of various strategies (such as tit-for-tat) when players who recognize each other meet repeatedly, and more recently with ensembles of strategies and with the effects of occasional errors. Here we neglect all strategical niceties or memories of past encounters, considering only two simple kinds of players: those who always cooperate and those who always defect. We explore the consequences of placing these players in a two-dimensional spatial array: in each round, every individual 'plays the game' with the immediate neighbours; after this, each site is occupied either by its original owner or by one of the neighbours, depending on who scores the highest total in that round; and so to the next round of the game. This simple, and purely deterministic, spatial version of the Prisoners' Dilemma, with no memories among players and no strategical elaboration, can generate chaotically changing spatial patterns, in which cooperators and defectors both persist indefinitely (in fluctuating proportions about predictable long-term averages). If the starting configurations are sufficiently symmetrical, these ever-changing sequences of spatial patterns—dynamic fractals—can be extraordinarily beautiful, and have interesting mathematical properties. There are potential implications for the dynamics of a wide variety of spatially extended systems in physics and biology.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
References
Axelrod, R. & Hamilton, W. D. Science 211, 1390–1396 (1981).
Axelrod, R. The Evolution of Cooperation (Basic Books, New York, 1984; reprinted by Penguin, Harmondsworth, 1989).
Nowak, M. A. & Sigmund, K. Nature 355, 250–253 (1992).
Nowak, M. A. & Sigmund, K. Acta. appl. Math. 20, 247–265 (1990).
Milinski, M. Nature 325, 434–435 (1987).
May, R. M. Nature 327, 15–17 (1987).
Nowak, M. A. & May, R. M. Int. J. Chaos Bifurc. (in the press)
Gardner, M. Sci. Am. 120–123 (October 1970).
Poundstone, W. The Recursive Universe (Morrow, New York, 1985).
Wolfram, S. Nature 311, 419–424 (1984).
Langton, C. G. Physica D22, 120–140 (1986).
Maynard Smith, J. Evolution and the Theory of Games (Cambridge Univ. Press, UK, 1982).
Hamilton, W. D. in Man and Best: Comparative Social Behaviour (eds Eisenberg, J. F. & Dillon, W. S.) (Smithsonian, Washington DC, 1971).
Wilson, D. S. The Natural Selection of Populations and Communities (Benjamin Cummings, Menlo Park, 1980).
Wilson, D. S., Pollock, G. B. & Dugatkin, L. A. Evol. Ecol 6, 331–341 (1992).
Axelrod, R. & Dion, D. Science 242, 1385–1390 (1988).
Lombardo, M. P. Science 227, 1363–1365 (1985).
Wilkinson, G. S. Nature 308, 181–184 (1984).
Eigen, M. & Schuster, P. Naturwissenschaften 64, 541 (1977).
Maynard Smith, J. Nature 280, 445–446 (1979).
Boeerlijst, M. C. & Hogeweg, P. Physica D48, 17–28 (1991).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Nowak, M., May, R. Evolutionary games and spatial chaos. Nature 359, 826–829 (1992). https://doi.org/10.1038/359826a0
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/359826a0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.