Abstract
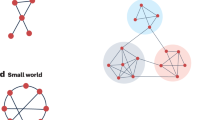
The study of networks pervades all of science, from neurobiology to statistical physics. The most basic issues are structural: how does one characterize the wiring diagram of a food web or the Internet or the metabolic network of the bacterium Escherichia coli? Are there any unifying principles underlying their topology? From the perspective of nonlinear dynamics, we would also like to understand how an enormous network of interacting dynamical systems — be they neurons, power stations or lasers — will behave collectively, given their individual dynamics and coupling architecture. Researchers are only now beginning to unravel the structure and dynamics of complex networks.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout








Similar content being viewed by others
References
Western Systems Coordinating Council (WSCC). Disturbance Report for the Power System Outage that Occurred on the Western Interconnection on August 10th, 1996 at 1548 PAST 〈http://www.wscc.com〉 (October 1996).
Anonymous. Media: Six degrees from Hollywood. Newsweek 11 October 1999, 6 (1999).
Kirby, D. & Sahre, P. Six degrees of Monica. New York Times 21 February 1998, op. ed. page (1998).
Cohen, J. E., Briand, F. & Newman, C. M. Community Food Webs: Data and Theory (Springer, Berlin, 1990).
Williams, R. J. & Martinez, N. D. Simple rules yield complex food webs. Nature 404, 180–183 (2000).
Kohn, K. W. Molecular interaction map of the mammalian cell cycle control and DNA repair systems. Mol. Biol. Cell 10, 2703–2734 (1999).
Hartwell, L. H., Hopfield, J. J., Leibler, S. & Murray, A. W. From molecular to modular cell biology. Nature 402, C47–C52 (1999).
Bhalla, U. S. & Iyengar, R. Emergent properties of networks of biological signalling pathways. Science 283, 381–387 (1999).
Jeong H., Tombor, B., Albert, R., Oltavi, Z. N., & Barabási, A.-L. The large-scale organization of metabolic networks. Nature 407, 651–654 (2000).
Broder, A. et al. Graph structure in the web. Comput. Netw. 33, 309–320 (2000).
Faloutsos, M., Faloutsos, P. & Faloutsos, C. On power-law relationships of the internet topology. Comp. Comm. Rev. 29, 251–262 (1999).
Achacoso, T. B. & Yamamoto, W. S. AY's Neuroanatomy of C. elegans for Computation (CRC Press, Boca Raton, FL, 1992).
Abello, J., Buchsbaum, A. & Westbrook, J. A functional approach to external graph algorithms. Lect. Notes Comput. Sci. 1461, 332–343 (1998).
Newman, M. E. J. The structure of scientific collaboration networks. Proc. Natl Acad. Sci. USA 98, 404–409 (2001).
Seglen, P. O. The skewness of science. J. Am. Soc. Inform. Sci. 43, 628–638 (1992).
Redner, S. How popular is your paper? An empirical study of the citation distribution. Eur. J. Phys. B 4, 131–134 (1998).
Davis, G. F. The significance of board interlocks for corporate governance. Corp. Govern. 4, 154–159 (1996).
Wilson, E. O. Consilience p.85 (Knopf, New York, 1998).
Weiss, C. O. & Vilaseca, R. Dynamics of Lasers (VCH, Weinheim, 1991).
Winful, H. G. & Wang, S. S. Stability of phase locking in coupled semiconductor laser arrays. Appl. Phys. Lett. 53, 1894–1896 (1988).
Li, R. D. & Erneux, T. Preferential instability in arrays of coupled lasers. Phys. Rev. A 46, 4252–4260 (1992).
Fabiny, L., Colet, P., Roy, R. & Lenstra, D. Coherence and phase dynamics of spatially coupled solid-state lasers. Phys. Rev. A 47, 4287–4296 (1993).
Kourtchatov, S. Yu., Likhanskii, V. V., Naparotovich, A. P., Arecchi, F. T. & Lapucci, A. Theory of phase locking of globally coupled laser arrays. Phys. Rev. A 52, 4089–4094 (1995).
Kozyreff, G., Vladimirov, A. G. & Mandel, P. Global coupling with time delay in an array of semiconductor lasers. Phys. Rev. Lett. 85, 3809–3812 (2000).
Winfree, A. T. The Geometry of Biological Time (Springer, New York, 1980).
Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence (Springer, Berlin, 1984).
Wiesenfeld, K., Colet, P. & Strogatz, S. H. Frequency locking in Josephson arrays: connection with the Kuramoto model. Phys. Rev. E 57, 1563–1569 (1998).
Turcotte, D. L. Fractals and Chaos in Geology and Geophysics 2nd edn (Cambridge Univ. Press, Cambridge, 1997).
May, R. M. Stability and Complexity in Model Ecosystems (Princeton Univ. Press, Princeton, 1973).
Levin, S. A., Grenfell, B. T., Hastings, A. & Perelson, A. S. Mathematical and computational challenges in population biology and ecosystem science. Science 275, 334–343 (1997).
Arbib, M. (ed.) The Handbook of Brain Theory and Neural Networks (MIT Press, Cambridge, MA, 1995).
Pantaleone, J. Stability of incoherence in an isotropic gas of oscillating neutrinos. Phys. Rev. D 58, 3002 (1998).
Stein, D. L. (ed.) Lectures in the Sciences of Complexity (Addison-Wesley, Reading, MA, 1989).
Pecora, L. M., Carroll, T. L., Johnson, G. A., Mar, D. J. & Heagy, J. F. Fundamentals of synchronization in chaotic systems: concepts and applications. Chaos 7, 520–543 (1997).
VanWiggeren, G. D. & Roy, R. Communication with chaotic lasers. Science 279, 1198–1200 (1998).
Collins, J. J. & Stewart, I. Coupled nonlinear oscillators and the symmetries of animal gaits. J. Nonlin. Sci. 3, 349–392 (1993).
Pérez, C. J., Corral, A., Diáz-Guilera, A., Christensen, K. & Arenas, A. On self-organized criticality and synchronization in lattice models of coupled dynamical systems. Int. J. Mod. Phys. B 10, 1111–1151 (1996).
Peskin, C. S. Mathematical Aspects of Heart Physiology 268–278 (Courant Institute of Mathematical Sciences, New York, 1975).
Mirollo. R. E. & Strogatz, S. H. Synchronization of pulse-coupled biological oscillators. SIAM J. Appl. Math. 50, 1645–1662 (1990).
Abbott, L. F. & van Vreeswijk, C. Asynchronous states in neural networks of pulse-coupled oscillators. Phys. Rev. E 48, 1483–1490 (1993).
Bressloff, P. C. Mean-field theory of globally coupled integrate-and-fire neural oscillators with dynamic synapses. Phys. Rev. E 60, 2160–2170 (1999).
Golomb, D. & Hansel, D. The number of synaptic inputs and the synchrony of large, sparse neuronal networks. Neural Comput. 12, 1095–1139 (2000).
Hopfield, J. J. Neurons, dynamics, and computation. Phys. Today 47, 40–46 (1994).
Winfree, A. T. Biological rhythms and the behavior of populations of coupled oscillators. J. Theor. Biol. 16, 15–42 (1967).
Strogatz, S. H. From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Physica D 143, 1–20 (2000).
Sakaguchi, H., Shinomoto, S. & Kuramoto, Y. Local and global self-entrainments in oscillator lattices. Prog. Theor. Phys. 77, 1005–1010 (1987).
Daido, H. Lower critical dimension for populations of oscillators with randomly distributed frequencies: a renormalization-group analysis. Phys. Rev. Lett. 61, 231–234 (1988).
Ermentrout, G. B. & Kopell, N. Frequency plateaus in a chain of weakly coupled oscillators. SIAM J. Math. Anal. 15, 215–237 (1984).
Kopell, N. & Ermentrout, G. B. Symmetry and phaselocking in chains of weakly coupled oscillators. Commun. Pure Appl. Math. 39, 623–660 (1986).
Sigvardt, K. A. & Williams, T. L. Models of central pattern generators as oscillators: the lamprey locomotor CPG. Semin. Neurosci. 4, 37–46 (1992).
Kauffman, S. At Home in the Universe (Oxford, New York, 1995).
Erdös, P. & Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 5, 17–61 (1960).
Bollobás, B. Random Graphs (Academic, London, 1985).
Kauffman, S. A. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 22, 437–467 (1969).
Kephart, J. O. & White, S. R. in Proc. 1991 IEEE Comput. Soc. Symp. Res. Security Privacy 343–359 (IEEE Computer Society Press, Los Alamitos, CA, 1991).
Watts, D. J. & Strogatz S. H. Collective dynamics of 'small-world' networks. Nature 393, 440–442 (1998).
Watts, D. J. Small Worlds (Princeton Univ. Press, Princeton 1999).
Wasserman, S. & Faust. K. Social Network Analysis: Methods and Applications (Cambridge Univ. Press, New York, 1994).
Wagner, A. & Fell, D. The small world inside large metabolic networks. Preprint available at 〈http://www.santafe.edu/sfi/publications/Abstracts/00-07-041abs.html〉 (2000).
Adamic, L. The small world web. Lect. Notes Comput. Sci. 1696, 443–452 (Springer, New York, 1999).
Kogut, B. & Walker, G. Small worlds and the durability of national networks: ownership and acquisitions in Germany. Am. Sociol. Rev. (in the press).
Amaral, L. A. N., Scala, A., Barthélémy, M. & Stanley, H. E. Classes of behavior of small-world networks. Proc. Natl Acad. Sci. USA 97, 11149–11152 (2000).
Stephan, K. E. et al. Computational analysis of functional connectivity between areas of primate visual cortex. Phil. Trans. R. Soc. Lond. B 355, 111–126 (2000).
Sporns, O., Tononi, G. & Edelman, G. M. Theoretical neuroanatomy: relating anatomical and functional connectivity in graphs and cortical connection matrices. Cereb. Cortex 10, 127–141 (2000).
Walsh, T. in Proc. 16th Int. Joint Conf. Artif. Intell. 1172–1177 〈http://dream.dai.ed.ac.uk/group/tw/papers/wijcai99.ps〉
Kleinberg, J. M. Navigation in a small world. Nature 406, 845 (2000).
Milgram, S. The small world problem. Psychol. Today 2, 60–67 (1967).
Wallinga, J., Edmunds, K. J. & Kretzschmar, M. Perspective: human contact patterns and the spread of airborne infectious diseases. Trends Microbiol. 7, 372–377 (1999).
Ball, F., Mollison, J. & Scalia-Tomba, G. Epidemics with two levels of mixing. Ann. Appl. Probab. 7, 46–89 (1997).
Keeling, M. J. The effects of local spatial structure on epidemiological invasions. Proc. R. Soc. Lond. B 266, 859–867 (1999).
Boots, M. & Sasaki, A. 'Small worlds' and the evolution of virulence: infection occurs locally and at a distance. Proc. R. Soc. Lond. B 266, 1933–1938 (1999).
Lago-Fernandez, L. F., Huerta, R., Corbacho, F. & Sigüenza, J. Fast response and temporal coherent oscillations in small-world networks. Phys. Rev. Lett. 84, 2758–2761 (2000).
Barthélémy, M. & Amaral, L. A. N. Small-world networks: evidence for a crossover picture. Phys. Rev. Lett. 82, 3180–3183 (1999).
Newman, M. E. J. Models of the small world: a review. J. Stat. Phys. 101, 819–841 (2000).
Newman, M. E. J., Moore, C. & Watts, D. J. Mean-field solution of the small-world network model. Phys. Rev. Lett. 84, 3201–3204 (2000).
Barbour, A. D. & Reinert, G. Small worlds. Preprint cond-mat/0006001 at 〈http://xxx.lanl.gov〉 (2000).
Barabási, A. L. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).
Barabási, A.-L., Albert, R. & Jeong, H. Mean-field theory for scale-free random networks. Physica A 272, 173–197 (1999).
Bernard, H. R., Killworth, P. D., Evans, M. J., McCarty, C. & Shelley, G. A. Studying social relations cross-culturally. Ethnology 27, 155–179 (1988).
Simon, H. A. On a class of skew distribution functions. Biometrika 42, 425–440 (1955).
Bornholdt, S. & Ebel, H. World-Wide Web scaling exponent from Simon's 1955 model. Preprint cond-mat/0008465 at 〈http://xxx.lanl.gov〉 (2000).
Albert, R. & Barabási, A.-L. Topology of evolving networks: local events and universality. Phys. Rev. Lett. 85, 5234–5237 (2000).
Dorogovtsev, S. N. & Mendes J. F. F. Evolution of networks with aging of sites. Phys. Rev. E 62, 1842–1845 (2000).
Krapivsky, P. L., Redner, S. & Leyvraz, F. Connectivity of growing random networks. Phys. Rev. Lett. 85, 4629–4632 (2000).
Albert, R., Jeong, H. & Barabasi, A.-L. Error and attack tolerance of complex networks. Nature 406, 378–382 (2000).
Cohen, R., Erez, K., ben-Avraham, D. & Havlin, S. Resilience of the Internet to random breakdowns. Phys. Rev. Lett. 85, 4626–4628 (2000).
Callaway, D. S., Newman, M. E. J., Strogatz, S. H. & Watts, D. J. Network robustness and fragility: percolation on random graphs. Phys. Rev. Lett. 85, 5468–5471 (2000).
Molloy, M. & Reed, B. A critical point for random graphs with given degree sequence. Random Struct. Algorithms 6, 161–179 (1995).
Molloy, M. & Reed, B. The size of the giant component of a random graph with given degree sequence. Combinatorics Probab. Comput. 7, 295–305 (1998).
Aiello, W., Chung, F. & Lu, L. A random graph model for power law graphs. Exp. Math. (in the press); preprint available at 〈http://math.ucsd.edu/~fan/power.pdf〉.
Newman, M. E. J., Watts, D. J. & Strogatz, S. H. Random graphs with arbitrary degree distribution and their applications. Preprint cond-mat/0007235 at 〈http://xxx.lanl.gov〉 (2000).
Watts, D. J. A simple model of fads and cascading failures. Preprint available at 〈http://www.santafe.edu/sfi/publications/Abstracts/00-12-062abs.html〉 (2000).
Cherniak, C. Component placement optimization in the brain. J. Neurosci. 14, 2418–2427 (1994).
Mitchison, G. Neuronal branching patterns and the economy of cortical wiring. Proc. R.. Soc. Lond. B 245, 151–158 (1991).
West, G. B., Brown, J. H. & Enquist, B. J. The fourth dimension of life: fractal geometry and the allometric scaling of organisms. Science 284, 1677–1679 (1999).
Banavar, J. R., Colaiori, F., Flammini, A., Maritan, A. & Rinaldo, A. Topology of the fittest transportation network. Phys. Rev. Lett. 84, 4745–4748 (2000).
Strogatz, S. H. Nonlinear Dynamics and Chaos (Perseus, New York, 1994).
Acknowledgements
Thanks to J. Ariaratnam, A.-L. Barabasi, N. Martinez, M. E. J. Newman, D. Watts and A. Winfree for their comments on a draft of the manuscript, and to R. Albert, L. Amaral, M. Amin, W. Blake, A. Broder, D. Callaway, J. Collins, G. Davis, H. Ebel, K. Kohn, N. Martinez, R. Oliva, M. E. J. Newman, J. Thorp, D. Watts, J. Wiener, A. Winfree and H. Wang for providing data, figures and information. Research supported in part by the National Science Foundation, Department of Defense, and Electric Power Research Institute.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Strogatz, S. Exploring complex networks. Nature 410, 268–276 (2001). https://doi.org/10.1038/35065725
Issue Date:
DOI: https://doi.org/10.1038/35065725
This article is cited by
-
Validating an algebraic approach to characterizing resonator networks
Scientific Reports (2024)
-
Diversity of information pathways drives sparsity in real-world networks
Nature Physics (2024)
-
Altered grey matter structural covariance in chronic moderate–severe traumatic brain injury
Scientific Reports (2024)
-
Identifying interactions among air pollutant emissions on diabetes prevalence in Northeast China using a complex network
International Journal of Biometeorology (2024)
-
Complex network analysis and robustness evaluation of spatial variation of monthly rainfall
Stochastic Environmental Research and Risk Assessment (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.