New Class of Gravitational Wave Detectors

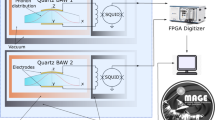
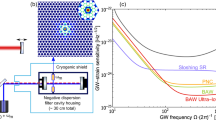
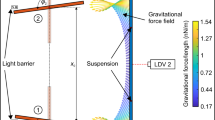
Abstract

IN a series of classic articles, Weber^1–3 derived the equations of motion and the response of mass quadrupole detectors to tensor gravitational waves. He has also constructed a detector which is a cylindrical rod tuned to its fundamental longitudinal acoustic resonance. These devices (class 1 detectors) have a definite relationship between the resonant frequency and the dimensions, in consequence of which they become very large (and expensive) at low frequencies. Using a somewhat arbitrary criterion (discussed later), one may state that class 1 detectors are difficult to build at frequencies below 1,000 Hz. There are other mechanically resonant devices (for example, tuning forks, rings and hollow “squares”), which we call class 2 detectors, which have a different relationship between the resonant frequency and their dimensions. Application of the same arbitrary criterion to class 2 detectors establishes that their useful frequency range can be extended to ∼30 Hz and that their sensitivity at the lower frequencies is comparable with class 1 detectors. Thus class 2 detectors are useful in a frequency range not easily accessible to class 1 detectors.