Abstract
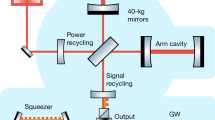
Nearly all theoretical approaches to the unification of quantum mechanics and gravity predict 1, 2, 3, 4 that, at very short distance scales, the classical picture of space-time breaks down, with space-time becoming somewhat ‘fuzzy’ (or ‘foamy’). The properties of this fuzziness and the length scale that characterizes itsonset are potentially a means for determining which (if any) of the existing models of quantum gravity is correct. But it is generally believed 5 that these quantum space-time effects are too small to be probed by technologies currently available. Here Iargue that modern gravity-wave interferometers are sensitive enough to test certain space-time fuzziness models, because quantum space-time effects should provide an additional source of noise in the interferometers that can be tightly constrained experimentally. The noise levels recently achieved in one interferometer 6 are sufficient to rule out values of the length scale that characterizes one of the space-time fuzziness models down to the Planck length (∼10 −35 m) and beyond, while the sensitivity required to test another model should be achievable with interferometers now under construction.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
References
Wheeler, J. A. Relativity, Groups and Topology (eds De Witt, B. S. &De Witt, C. M.) (Gordon & Breach, New York, (1963).
Ashtekar, A., Rovelli, C. & Smolin, L. Weaving a classical geometry with quantum threads. Phys. Rev. Lett. 69, 237–240 (1992).
Ellis, J., Mavromatos, N. & Nanopoulos, D. V. String theory modifies quantum mechanics. Phys. Lett. B 293, 37–48 (1992).
Hawking, S. W., Page, D. N. & Pope, C. N. Quantum gravitational bubbles. Nucl. Phys. B 170, 283–306 ( 1980).
Isham, C. in Proc. 14th Int. Conf. on General Relativity and Gravitation (eds Francavaglia, M., Longhi, G., Lusanna, L. &Sorace, E.) (World Scientific, Singapores, (1997).
Abramovici, A. et al . Improved sensitivity in a gravitational wave interferometer and implications for LIGO. Phys. Lett. A 218, 157–163 (1996).
Garay, L. J. Quantum gravity and minimum length. Int. J. Mod. Phys. A 10, 145–166 (1995).
Bergmann, P. G. & Smith, G. J. Measurability analysis of the linearized gravitational field. Gen. Rel. Grav. 14, 1131–1166 ( 1982).
Diosi, L. & Lukacs, B. On the minimum uncertainty of space-time geodesics. Phys. Lett. A 142, 331– 334 (1989).
Ng, Y. J. & Van Dam, H. Limit to space-time measurement. Mod. Phys. Lett. A 9, 335– 348 (1994).
Ahluwalia, D. V. Quantum measurement, gravitation, and locality. Phys. Lett. B 339, 301–303 (1994).
Amelino-Camelia, G. Limits on the measurability of space-time distances in the semi-classical approximation of quantum gravity. Mod. Phys. Lett. A 9, 3415–3422 (1994).
Amelino-Camelia, G. Dimensionful deformations of Poincaré symmetries for a Quantum Gravity without ideal observers. Mod. Phys. Lett. A 13, 1319–1325 (1998).
Wigner, E. P. Relativistic invariance and quantum phenomena. Rev. Mod. Phys. 29, 255–268 ( 1957).
Bohr, N. & Rosenfeld, L. Zur Frage der Messbarkeit der Electromagnetischen Feldgrössen. Kongelige Danske Videnskabernes Selskab Matematisk-Fysiske Meddelelser 12, 1– 65 (1933).
Radeka, V. Low-noise techniques in detectors. Annu. Rev. Nucl. Part. Sci. 38, 217–277 ( 1988).
Karolyhazy, F. Gravitation and Quantum Mechanics of macroscopic objects. Il Nuovo Cimento A 42, 390–402 ( 1966).
Colella, R., Overhauser, A. W. & Werner, S. A. Observation of gravitationally induced quantum interference. Phys. Rev. Lett. 34, 1472– 1474 (1975).
Amati, D., Ciafaloni, M. & Veneziano, G. Superstring collisions at Planckian energies. Phys. Lett. B 197, 81–88 (1987).
Kempf, A., Mangano, G. & Mann, R. B. Hilbert space representation of the minimal length uncertainty relation. Phys. Rev. D 52, 1108– 1118 (1995).
Lukierski, J., Nowicki, A. & Ruegg, H. Classical and quantum-mechanics of free κ-relativistic systems. Annu. Phys. 243, 90– 116 (1995).
Amelino-Camelia, G. Enlarged bound on the measurability of distances and quantum κ-Poincaré group. Phys. Lett. B 392, 283– 286 (1997).
Amelino-Camelia, G., Ellis, J., Mavromatos, N. E. & Nanopoulos, D. V. Distance measurement and wave dispersion in a Liouville string approach to quantum gravity. Int. J. Mod. Phys. A 12, 607–623 (1997).
Saulson, P. R. Fundamentals of Interferometric Gravitational Wave Detectors (World Scientific, Singapore, (1994).
Abramovici, A. et al . LIGO: The Laser Interferometer Gravitational-Wave Observatory. Science 256, 325–333 (1992).
Bradaschia, C. et al . The VIRGO project: a wide band antenna for gravitational wave detection. Nucl. Instrum. Meth. A 289, 518–525 (1990).
Danzmann, K. LISA: Laser interferometer space antenna for gravitational wave measurements. Class. Quant. Grav. 13, A247– A250 (1996).
Ellis, J., Hagelin, J. S., Nanopoulos, D. V. & Srednicki, M. Search for violations of Quantum Mechanics. Nucl. Phys. B 241, 381–405 (1984).
Amelino-Camelia, G., Ellis, J., Mavromatos, N. E., Nanopoulos, D. V. & Sarkar, S. Tests of quantum gravity from observations of γ-ray bursts. Nature 393, 763– 765 (1998).
Ahluwalia, D. V. Can general relativistic description of gravitation be considered complete? Mod. Phys. Lett. A 13, 1393– 1400 (1998).
Snadden, M. J., McGuirk, J. M., Bouyer, P., Haritos, K. G. & Kasevich, M. A. Measurement of the Earth's gravity gradient with an atom interferometer-based gravity gradiometer. Phys. Rev. Lett. 81, 971–974 (1998).
Service, R. F. Gravity measurements ride the atom wave. Science 281 , 762–763 (1998).
Seife, C. Einstein in free fall. New Sci. 158, 11 (1998).
Acknowledgements
I thank A. Ashtekar for suggesting that gravity‐wave interferometers might be useful for experimental tests of some quantum‐gravity phenomena; D. Ahluwalia, J. Ellis, J. Lukierski, N. E. Mavromatos, C. Rovelli, S. Sarkar and J. Stachel for discussions about quantum‐gravity models; and F. Barone, M. Coles, J. Faist, R. Flaminio, L. Gammaitoni, G. Gonzalez, T. Huffman, L. Marrucci and M. Punturo for conversations about experimental interferometry. This work was supported by the Swiss National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Amelino-Camelia, G. Gravity-wave interferometers as quantum-gravity detectors. Nature 398, 216–218 (1999). https://doi.org/10.1038/18377
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/18377
This article is cited by
-
Quantum gravity, minimum length and holography
Pramana (2021)
-
A Planck-scale limit on spacetime fuzziness and stochastic Lorentz invariance violation
Nature Physics (2015)
-
Optomechanically induced transparency in the presence of an external time-harmonic-driving force
Scientific Reports (2015)
-
Gravitational bar detectors set limits to Planck-scale physics on macroscopic variables
Nature Physics (2013)
-
Shedding light on the fabric of space-time
Nature (2011)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.