Introduction

The functional connectivity (FC) of brain networks, that is, relationships among nodes inferred from the dynamics, provides a condensed way of exploring the organization of excitable dynamics on neural graphs. It is also an important marker for the link between neural network topology and dynamics. The overall agreement between functional connectivity and structural connectivity (SC) in neural systems has been studied in experimental data1,2,3 as well as simulations4,5,6. In particular, correlations of structural brain connectivity with functional connectivity derived from the BOLD signal in fMRI studies show high correlation values in the range of 0.6–0.8 in simulations and experimentally around 0.32,6,7,8.

Previous investigations of the relations between SC and FC, using a general model of excitable systems that is based on the deterministic discrete activation of nodes, found that the relation strongly depended on the structural network topology9. While sparse random networks displayed an anti-correlation between SC and FC, in modular networks SC and FC were strongly correlated. These effects can be understood within the stylized dynamics of the discrete excitable, SER model. Here, S-E-R denotes the basic node behavior of susceptible (S) nodes becoming excited (E) by excited neighbors, then refractory (R), before turning once again susceptible, in discrete time steps.

What the SER model offers is a detailed mechanistic understanding of how topology regulates particular contributions to the co-activation matrix and in this way determines functional connectivity: co-activation of two nodes arises from common neighbors. A link between two nodes tends to systematically reduce the likelihood of co-activation due to sequential excitation of the two nodes, leading in general to a negative correlation of structural and functional connectivity. However, global topological features can ‘override’ this tendency. Our previous investigations showed that a modular structure typically enhances positive correlations between structural and functional connectivity9. Qualitatively speaking, the mechanism behind this finding is as follows: high connectivity is associated with an elevated excitation density. Locally high connectivity (that is, within a module) results in a statistically higher number of excitations among nodes within the same module and, as a consequence, systematically higher co-activations of nodes in the same module. This positive contribution to the correlation between structural and functional connectivity tends to ‘overwrite’ the typically negative correlations arising from suppressed co-activity of linked nodes due to sequential excitation.

The discrete-excitable model thus provides us with a clear hypothesis of how structural connectivity is translated into functional connectivity. In the present study, we aimed to explore if these relations also hold for another well established model describing neural dynamics, the Fitzhugh-Nagumo model (FHN)10,11. The FHN model is appealing due to its biological motivation in general, the biologically plausible interpretation of its degrees of freedom and its widespread use in computational neuroscience (see, e.g.,12). There are also theoretical arguments for using this model as a coarse-grained representation of the dynamics of cortical areas13. Furthermore, this model is free from discretization artifacts that potentially affect the interpretation of results arising from the discrete-excitable model, as the FHN model operates on continuous time and state spaces.

Our general aim is to highlight model-independent relations of the SC-FC relationship to the underlying topological architecture of SC. To this end, we explored the relationship of SC-FC by a systematic variation and randomization of modular networks.

Results

We implemented stochastic versions of two well-established computational models of brain activity, SER nodes and FHN oscillators, that are capable of reproducing different aspects of empirical functional connectivity as observed in resting-state fMRI data14,15. To investigate the influence of topology, we used a synthetic flat modular network that was iteratively randomized. At each iteration, FC was derived from simulations by both models and then the correlations between SC and FC were computed. Simulations were carried out over 50 realizations (see Methods). While, initially, the two dynamic models appeared to yield different findings for the SC-FC relationship across the range of network randomization, an adjustment of the time window from which FC was derived demonstrated the overall similarity of the SC-FC relations.

Findings by the SER versus FHN model

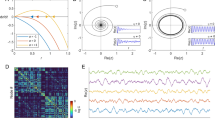
Using the stochastic SER model, we here reproduced the effect of modularity on the SC-FC relationship, as observed by9 for the deterministic version of the model. While the modular networks showed a high SC-FC correlation, moving toward random networks destroyed this relationship (Figure 1). Of note, we here investigated the SC-FC relationship in a somewhat different way compared to9. In Ref. 9, the correlation between SC and FC was calculated with FC thresholded at different densities, while here we directly correlated SC with FC (unthresholded). Thus, a high correlation between SC and FC is clearly supported by network modularity. For the FHN model, by contrast, we observed a high and almost constant correlation between SC and FC whatever the underlying topology (Figure 1). Generally, these SC-FC relationship remained qualitatively similar across a wide range of parameters for both models (see Supplementary Figure S1).

Figure 1
figure 1

Illustration of the SC-FC relationship in the SER and FHN model.

(Left) SC-FC correlation across the range of randomization in both models. (Right) Illustration of the SC patterns (binary, black entries denote the presence of connections) and FC patterns (weighted, colors code for the strength of FC, see associated color bar) for the two extreme cases of network organization (i.e., original modular SC, top and its fully randomized version, bottom). Each row and column of the matrices represents a node of the network.

Full size image

Particularly, comparing the behavior of the SER and the FHN models in Figure 1, we observe a striking discrepancy: The FHN produces high correlations between structural and functional connectivity with only little impact of the global topological feature of modularity. By contrast, the discrete excitable SER model is highly sensitive to the topological feature of modularity, as it shows a high SC-FC correlation (based on FC derived from co-activations) for the modular network, while this correlation vanishes with increasing network randomization.

How can the apparent discrepancy between the two models be explained and potentially be resolved? When exploring the spiking activity of the FHN model, we observed a spread of time delays between spikes as well as variation in the actual width of the spikes. Most of the spiking activity occurred within a window of ~100 ms while the average spiking window width was estimated at ~60 ms (Figure 2). This spread is in contrast to the very precise activation behavior of the discrete SER model, where the ‘spiking’ lasts for exactly one time step. Consequently, we explored how these different time windows, on which the calculation of the FC is based, may have affected the relationship of SC-FC relationship.

Figure 2
figure 2

Illustration of the FHN dynamics.

(Top) Example of two time series. (Bottom) Estimated width of spikes and time delays between spikes.

Full size image

Resolving SER - FHN discrepancies by adjusting time windows for FC

The comparatively broad spikes in the FHN model lead to an imprecise separation of concurrent co-activations and sequential activations, two event categories precisely separated by definition in the SER model. We hypothesized that a clearer separation of the two events in the FHN model would bring the results for SC-FC correlations substantially closer to those of the SER model, thus resolving the initially apparent discrepancy. In order to investigate this hypothesis, we, first, defined the time point of spiking in the FHN model more precisely (see Methods), in order to be in line with the discrete spiking of the SER model and, second, in both models varied the time window from which ‘simultaneous’ events were drawn for the calculation of FC. Thus, in both models we explored the window length at which spikes occur. For the FHN model, the size of spiking windows is expressed in milliseconds, while in the SER model, the size is equal to the number of time steps. For both models, FC was calculated as the co-activations occurring during various window lengths.

Re-analyzed in such a way (i.e., by transforming continuous time windows to discrete time steps), the behavior of the FHN model closely resembled that of the SER model. When considering very short time integration windows (e.g. 5% of the spike's width, that is ~3 ms), the FHN model behaved very similarly to the SER model; specifically, destroying modularity in the FHN model also abolished the SC-FC correlation (Figure 3, see Figure 4 for longer time integration ranges). By contrast, when considering longer integration windows (~20 ms), we reproduced the effect observed when using continuous time series and correlation as a measure of FC. In the SER model, the same effects were present, although more pronounced, with an apparent strong correlation across the whole range of randomization only at a one-step delay window.

Figure 3
figure 3

Time integration.

(Left) SC-FC correlations from the SER with instantaneous time integration (blue, as in Figure 1) and one step time integration (green). (Right) SC-FC correlations from the FHN with SER-like co-activation FC as a function of time integration window length (in milliseconds) from narrow, blue, to large, green) as well as with FC from correlation as in Figure 1 (black).

Full size image
Figure 4
figure 4

Time integration.

(Left) SC-FC correlations from the SER with various time integration in steps. (Right) SC-FC correlations from the FHN with SER-like co-activation FC as a function of time integration window length.

Full size image

Discussion

By comparing two different models of excitable neural nodes across a range of network architecture from modular to random wiring, we gathered insights into effects of network topology underlying functional connectivity.

As the close investigation of the FHN model revealed, the definition of functional connectivity, via the cross-correlation coefficient between the time series of two nodes, in the FHN model includes contributions from instantaneous co-activations as well as sequential activations. This lack of discrimination of two formally different signals is responsible for the high correlation coefficient between SC and FC even in random, unstructured graphs. A similar effect can be reproduced in the SER model, by increasing the time integration window for co-activations and thus convolving simultaneous and sequential activations.

The time integration window length is constrained by the underlying dynamical process. Given the discrete update rules for the SER model, windows of length 0 (co-activations) and 1 (sequential activations) can capture the entire dynamic connectivity. For continuous models, such as the FHN model, the time window length must be small enough to capture co-activations (theoretically, of the size of the time resolution employed). At slightly larger integration windows, simultaneous and sequential events mix and result in a high correlation of SC-FC, independent of the modular network topology. At even longer time windows (substantially longer than the time scale of spiking events), spikes blur that arise from across the whole network at different times, and, thus, the FC generally does no longer reflect the characteristic network topology (Figure 4).

Discrete models need to be used with a certain care, as some dynamical effects produced by them may indeed be artifacts of the (time and state) discretizations. However, their potential to unambiguously distinguish events as co-activations or sequential activations makes such discrete models powerful tools for exploring the mechanisms of how network architecture regulates some key features of excitable dynamics. In fact, it was the strong influence of modular network topology on the SC-FC relationship, observed when using a deterministic version of the SER9, that inspired the hypothesis of the present analysis.

Our assessment of the microscopic and mechanistic underpinnings of the relationship between structural and functional connectivity presented here is by no means intended as an attempt to redefine functional connectivity and base it on discrete activation events. A multitude of significant biological mechanisms and effects can contribute via statistical blurring, coarse-graining or time integration of signals to a meaningful mixing of what we labeled ‘co-activation’ and ‘sequential activation’ of nodes. Indeed, we also analyzed the consequences of deriving the FC from a simulated BOLD signal, implemented as a forward model for both the SER and the FHN mechanisms, rather than deriving the FC directly from the excitable dynamics. Due to its broad shape, the BOLD signal convolved instantaneous and sequential events of the underlying dynamics, so that SC-FC correlations that were derived from the simulated BOLD signals in both models were non-zero (on average ~0.2) and constant across the whole range of network variation from modular to random. Thus, it may not be possible to study the influence of neural network topology on the SC-FC relationship using experimental approaches that are based on coarse activation signals, such as fMRI. However, such topological contributions may be ultimately experimentally revealed by techniques that can observe neural signals at a finer temporal resolution, such as microelectrode recordings16. In general, we would like to emphasize that the predictions from the discrete-excitable SER model for SC-FC correlations, in spite of the apparent first-glance discrepancies, can be brought into an excellent agreement with predictions from more realistic numerical simulations and empirical evidences.

With its small number of parameters and its sensitivity to network properties, the SER model is capable of serving as a ‘microscope’ for the mechanistic underpinning of the relationship between structural and functional connectivity. Figure S1 shows the change of SC-FC correlations under randomization for different settings of the parameters f (rate of spontaneous activation) and p (recovery rate) of the SER model. First of all, the change of SC-FC correlations under randomization of the modular network is qualitatively preserved over a wide range of parameter values. If one focuses on the first point in each curve, however, that is the SC-FC correlation for the original modular network, one can see that at fixed f the SC-FC correlations first increase and then decrease with the recovery probability p (unless f is very small). Thus there is a range in p where the structural modules are best ‘detected’ by the dynamics represented in the functional connectivity. This is an example of how the choice of parameter values in the dynamical model can influence how strongly certain topological properties enter SC-FC correlations.

Minimal models have been outstandingly successful in other fields. After their first formulation as abstractions of gene regulatory networks17, Boolean models went through a long phase with attention coming mostly from a purely theoretical perspective, until in the early 2000 s dramatic successes of explaining complex biological phenomena (segment polarity network of Drosophila18; cell cycle of baker's yeast19 and fission yeast20, including the prediction of mutant phenotypes21) have established Boolean models as a core modeling technique for gene regulatory systems and signaling pathways22, see also23.

Similarly, in epidemic diseases, the simple SIR (‘susceptible-infected-recovered’) and SIS (‘susceptible-infected-susceptible’) models allowed understanding epidemic thresholds24. Related models have been used to understand how the epidemic threshold depends on network architecture (e.g., the strong decrease in small-world networks25 and the vanishing in scale-free networks26) and even paved the way towards the prediction of realistic spatial infection patterns, when constrained by a network of long-distance flight connections27.

Similar to these successes, our minimal SER model enables us to extract a few stylized facts about excitable dynamics on graphs28, by separating the logical organization (both, on the structural and functional level) from the physiological details of how this logical organization is implemented.

Methods

Network topology

Simulations were performed on a synthetic undirected flat modular network with 60 nodes and a density of 0.23. To investigate the effect of topology on the relationship between simulated FC and underlying SC, the original modular graph was randomized at various proportions from 0%, the original graph, to 100%, the completely randomly rewired network. Randomized networks were generated using a Markov switching algorithm that randomly swapped pairs of edges29. The set of randomized networks was degree-matched (both in-degree and out-degree of each node was preserved) and statistical assessment was performed by exploring 50 randomization of the original network for each proportion.

Models

We used a three-state cellular automaton model of excitable dynamics, the SER model, representing a stylized biological neuron or neural population. The SER model operates on discrete time and employs the following synchronous update rules:

  1. 1

    a node in the S state for one time step enters in a E state stochastically with a transition probability f or when at least one of its neighbors is excited;

  2. 2

    a node in the E state for one time step enters in a R state;

  3. 3

    a node in the R state for one time step enters in a S state stochastically with a recovery probability p.

For p = f = 1, we have a deterministic model, which was investigated in detail in Ref. 9, where the role of cycles in storing excitations and supporting self-sustained activity was elucidated. Let xi(t) ∈ {S, E, R} be the state of node i at time t. It is convenient to discuss the excitation pattern instead:

In this way, we can define FC as the co-activation of nodes,

For each network, we simulated 100 runs of 5 000 timesteps with random initial conditions and computed the average FC. The initial conditions were randomly generated with an equiprobability to set a node into one of the three states. The main results were obtained with f = 10−3 and p = 0.1, furthermore we have also explored the robustness over the parameter space.

Additionaly, we use the well-known Fitzhugh-Nagumo model10,11. The model is composed of two nested variables, the membrane potential x and a recovery variable y

where τ represent the time scale of each variable (τx = 2 ms and τy = 100 ms), D is the structural connectivity (i.e., the adjacency matrix of the underlying network), k is a global scaling parameter or coupling strength fixed at 0.2 and ν stand for an uncorrelated Gaussian noise with zero mean and unit variance whose amplitude is scaled by σ = 0.25. Parameter values are α = 0.8, β = 0.6 and γ = 1.

Simulations were performed using Euler integration with a time resolution of 1 ms and runs lasting 8 min. FC was defined as correlation between simulated time series. Moreover, we investigated the robustness of the findings across a subset of the parameters by varying in one case the timescales (i.e. τx and τy) and in another one the parameters α and β.

In order to reconcile the FHN model with the SER model, time-series were discretized and spikes detected. Spiking activity at each node from the FHN model was first normalized by subtracting its mean and dividing by its standard deviation. The detection threshold for spikes was determined as one, so any activity above this threshold was considered as spikes.