Abstract
We study theoretically and numerically the kinetics of the coefficient of friction of an elastomer due to abrupt changes of sliding velocity. Numerical simulations reveal the same qualitative behavior which has been observed experimentally on different classes of materials: the coefficient of friction first jumps and then relaxes to a new stationary value. The elastomer is modeled as a simple Kelvin body and the surface as a self-affine fractal with a Hurst exponent in the range from 0 to 1. Parameters of the jump of the coefficient of friction and the relaxation time are determined as functions of material and loading parameters. Depending on velocity and the Hurst exponent, relaxation of friction with characteristic length or characteristic time is observed.
Similar content being viewed by others
Introduction
Dry friction plays a decisive role in a great variety of physical processes and applications1,2. Very often the simplest friction “law” (Amontons' law3) is used to describe dry friction. It states that the force of friction, F, is proportional to the normal force, FN: F = μFN, the proportionality coefficient μ being called coefficient of friction. It is common understanding that Amontons' “law” is only a very rough “zeroth-order approximation”. Already Coulomb4 knew that the coefficient of sliding friction depends on sliding velocity and normal force and that static friction depends approximately logarithmically on time1. The explicit dependence of the coefficient of friction on time became a hot topic in the 1970s in the context of earthquake dynamics. Based on the experimental work on rocks by Dieterich5,6, Rice and Ruina7 have formulated a kinetic equation for friction, which became one of the most influential generalized “rate-state models”. Similar kinetic behavior of the coefficient of friction was observed on a variety of different materials including metals, paper and polymers8,9,10,11,12. Most physical interpretations of rate-state friction are based on the concept by Bowden and Tabor13 emphasizing the influence of the interaction of rough surfaces; they include direct observations of the contacting surfaces14 as well as theoretical analysis15,16. Other models for the kinetics of the friction coefficient were proposed based on the development of surface topography due to wear (Ostermeyer17,18) or shear melting of thin surface layers19. Heslot et. al.20 provided a very detailed experimental analysis of the dynamics of systems obeying the rate-state law of friction. The kinetics of the coefficient of friction is an essential factor for the stability of systems with friction21,22,23, the break-out instabilities24 as well as for the design of feedback control systems25,26,27 and remains a topic of high scientific and technological interest. Most rate-state formulations of frictional laws contain a characteristic length scale, at which a transition from sticking to sliding occurs. The existence of this length is typically associated with a characteristic size of asperities or with other structural peculiarities at the micro scale28,29.
In spite of the intensive research in the field of generalized laws of friction, both the form of the rate-state friction equations and their parameters can still only be determined empirically. In the present paper, we provide a theoretical analysis of the kinetics of the friction coefficient for one class of materials – elastomers. For these materials, parameters of the kinetic law of the coefficient of friction are connected with material, loading and surface parameters. We simulate the standard type of loading used to experimentally determine the parameters of the rate-state laws: one of the bodies in contact first slides with a constant velocity; at some moment of time, the sliding velocity changes abruptly and the jump of friction as well as the subsequent relaxation is observed. From these simulations we derive closed-form relations for the jump of friction and the characteristic time of the following relaxation.
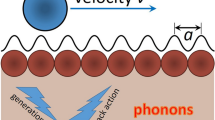
In studying the friction of elastomers we are going from the concept of Greenwood and Tabor about the rheological nature of elastomer friction30 which became widely accepted after the classical work by Grosch31. To arrive at a basic understanding of the dynamic behavior of the coefficient of friction, we use the one-dimensional model described in the reference32: (a) the elastomer is modeled as a simple Kelvin body, which is completely characterized by its static shear modulus G and viscosity η, (b) the non-disturbed surface of the elastomer is plane and frictionless, (c) the rigid counter body is assumed to have a randomly rough, self-affine fractal surface without long wave cut-off, (d) no adhesion or capillarity effects are taken into account, (e) thermal effects in micro contacts are neglected.
Based on the contact mechanics of both rotationally symmetric profiles33 and self-affine fractal surfaces34, it was recently suggested that the results obtained with one-dimensional foundations may have a broad area of applicability if the rules of the method of dimensionality reduction (MDR)35,36,37 are observed. The MDR was criticized by Lyashenko et. al. in the comment38. Counterarguments are presented in the reply39 as well as in the sections devoted to the areas of application of the MDR of the review paper35 and the monograph36. Here we only note that the one-dimensional MDR model conserves all essential characteristics of the original three-dimensional model such as rms surface roughness, gradient and curvature, self-similarity properties (Hurst exponent), normal stiffness and relaxation properties (in the case of the Kelvin body the relaxation time) and thus is suitable for at least qualitative analysis of the underlying three-dimensional friction model.
Results
One-dimensional model
According to the MDR, the Kelvin body can be modeled as a series of parallel springs with stiffness Δkz and dash pots with damping constant Δγ, where

The counter body is modeled as a rough line having the power spectral density C1D ∝ q−2H−1, where q is the wave vector and H the Hurst exponent. This power spectrum corresponds to the two-dimensional roughness with the power spectrum C2D ∝ q−2H−235,40. The spectral density is defined in the interval from qmin = 2π/L, where L is the system size, to the upper cut-off wave vector qmax = π/Δx. The spacing Δx determines the upper cut-off wave vector and is an essential physical parameter of the model. Surface topography is characterized by the rms roughness  , which is dominated by the long wavelength components of the power spectrum and the rms gradient of the surface
, which is dominated by the long wavelength components of the power spectrum and the rms gradient of the surface  , which is dominated by the short wavelength part of the spectrum. The rigid surface was generated according to the rules described in reference34 and periodic boundary conditions were used. The rigid surface was pressed against the elastomer with a normal force FN and moved tangentially with a constant velocity v (Figure 1).
, which is dominated by the short wavelength part of the spectrum. The rigid surface was generated according to the rules described in reference34 and periodic boundary conditions were used. The rigid surface was pressed against the elastomer with a normal force FN and moved tangentially with a constant velocity v (Figure 1).
The model is described in detail in reference32. Here we reproduce for convenience only the basic equations. If the rigid profile is given by z = z(x − vt) and the profile of the elastomer by u = u(x,t), then the normal force in each particular element of the viscoelastic foundation is given by

For the elements in contact with the rigid surface, this means that

where d is the indentation depth and z′(x) denotes a derivative with respect to x. For these elements, the condition of remaining in contact, f > 0, is checked in each time step. Elements out of contact are relaxed according to the equation f = 0: Gu(x) + ηu·(x,t) = 0 and the non-contact condition u < z is checked. The indentation depth d is determined to satisfy the condition of the constant normal force

where the integration is only over points in contact. A typical configuration of the contact is shown in Figure 1. The tangential force is calculated by multiplying the local normal force in each single element with the local surface gradient and subsequently summing over all elements in contact:

The coefficient of friction μ was calculated as the ratio of the tangential and normal force.
Due to the independence of the degrees of freedom, the algorithm is not iterative and there are no convergence problems. The length of the system was L = 0.01 m and the number of elements N = L/Δx was typically 5000. The shear modulus was G = 107 Pa. Instead of viscosity, the relaxation time τ = η/G = 10−3 s was used. The following ranges of parameters were covered in the present study: 11 values of the Hurst exponent ranging from 0 to 1; Normal forces FN ranging from 10−2 to 102 N; Δx ranging from 10−7 to 10−5 m; roughness ranging from 10−6 to 10−4 m; velocities v1 from 10−4 to 101 m/s; velocity jumps Δv from −0.2v1 to 0.3v1. All values shown below were obtained by averaging over 200 realizations of the rough surface for each set of parameters.
Relaxation of friction after a velocity jump
With the model described previously, the following numerical experiments were carried out: the rigid body was first moved with velocity v1, at the time moment t0 the velocity was abruptly changed to a new value v2 which could be larger or smaller than the initial value. The typical behavior of the coefficient of friction before, during and after the velocity jump is shown in Figure 2.
The initial value of the coefficient of friction before the jump and the final value after relaxation are of course just the values of the coefficient of friction for stationary sliding which have been studied in reference32 and are reproduced for one set of material and loading parameters in Figure 3a. With the same parameters, Figure 3b shows the kinetic coefficients of friction changing with time for several velocities in the entire range used in Figure 3a where the sliding velocity is increased by 20% at the moment t/τ = 10. In the present paper, we studied the complete range of velocities: region I where the friction coefficient increases approximately linearly with velocity, the transition region II and the plateau III (Figure 3a).
The relaxation of the coefficient of friction after the jump can be accurately fitted by an exponential function of the form

where

An example fit is shown in Figure 4. According to equation (6), the coefficient of friction at the moment t = t0 is equal to μ(t0) = μ*+μ2 = μ1 + Δμ0, then we have

The kinetic behavior is therefore completely determined by the value Δμ0 of the jump of the coefficient of friction and its relaxation time.
Fitting with an exponential function, equation (6) (b = 2.4), for the data set: FN = 1.2 N, L = 0.01 m, h = 10−5 m, G = 107 Pa, τ = 10−3 s, Δv = 0.2v1, v1 = 0.05 m/s and H = 0.7.
We firstly consider the value Δμ0 at the time of jump t = t0. For very small velocity jumps, both the immediate increase of the coefficient of friction, Δμ0 and the difference between the asymptotic values μ2 − μ1, are proportional to the velocity change:

In the limit of small velocities, (region I, corresponding to the linear dependence of the coefficient of friction on velocity), both ζ and ξ are close to 1. It means that μ jumps directly to the value μ2, so that there is practically no subsequent relaxation. This behavior can be clearly observed in Figure 3b.
Figure 5 shows that the velocity dependence of Δμ0 is similar to that of the coefficient of friction μ1 studied in the reference32. In particular, Δμ0 first increases linearly with velocity and then approaches a plateau. The results from simulations with different Δv and different Hurst exponents prove that the linear part of this dependency can be universally described by described by equation:

while at the plateau the relation

is valid. These equations can be combined to the following interpolation equation

where we introduced normalized quantities  and
and  . The quality of this approximation is illustrated in Figure 6 by comparison with numerical results for 11 Hurst exponents.
. The quality of this approximation is illustrated in Figure 6 by comparison with numerical results for 11 Hurst exponents.
Approximation of equation (12) for 11 Hurst exponents from 0 to 1.
Other parameters: FN = 1.2 N, L = 0.01 m, h = 10−5 m, G = 107 Pa, τ = 10−3 s and Δv = 0.2v1.
Let us now consider the relaxation behavior after the jump. We found that the simulation results for the coefficient b in equation (6) can be described accurately by the empirical equation

where α is a coefficient which depends only on the Hurst exponent. Figure 7 shows the dependence of the coefficient b on the combination v1τqmax for different Hurst exponents. For v1τqmax < 1 (left part in Figure 7), the coefficient α is practically constant: α ≈ 1, while for v1τqmax > 1 it can be approximated as α ≈ 1 − H (Figure 8).
Dependence of the power α in equation (13) on the Hurst exponent for v1τqmax > 1.
Discussion
We investigated the kinetics of the coefficient of friction after a jump of sliding velocity for a model elastomer. We found a simple general structure of the kinetics: the coefficient of friction first experiences a jump, followed by relaxation according to an exponential law to the new stationary value. The jump Δμ0 of the coefficient of friction and the relaxation time are thus the only quantities which describe completely the kinetics of the coefficient of friction. For the model elastomer studied, we found closed form relations for both Δμ0 and the relaxation time as functions of material and loading parameters. The character of the relaxation is governed by the quantity v1τqmax, which can be considered as the ratio of two characteristic times of the system: the relaxation time τ of the elastomer and the typical time of contact of micro asperities 1/(v1qmax). For v1τqmax < 1, the coefficient b in equation (6) is approximately equal to b ≈ v1τqmax, so the relaxation of the coefficient of friction is given by the equation

Note that in this region relaxation of the coefficient of friction occurs at a characteristic length Dc = 1/qmax, which has the same order of magnitude as the size of micro contacts between the bodies, in accordance with the initial concept of Dieterich et. al.14. For v1τqmax > 1, the relaxation of the coefficient of friction is described as

with the characteristic relaxation time

Equation (15) covers the limiting cases of relaxation at a characteristic length 1/qmax (in the limit H = 0) and of relaxation at a characteristic time τ (in the limit H = 1).
Methods
For construction of one-dimensional models, we used the Method of Dimensionality Reduction (MDR). With this method a three-dimensional contact is mapped onto a one-dimensional one with properly defined elastic or viscoelastic foundations. It provides exact solutions for the normal contact problem of axially symmetric and self-affine fractal surfaces as well as exact solutions for the tangential contact problem with a constant coefficient of friction. All properties which depend on the force-displacement relationship such as contact stiffness, electrical resistance and thermal conductivity, as well as frictional force for elastomers can be analyzed with this method. The fundamentals and basic rules are described in detail in the paper35 and in the book36,41. More descriptions related to viscoelastic contact can also be found in the introduction and at the beginning of the Section Results. In Ref. 38, it was stated that the MDR cannot correctly describe the effects of elastic interactions in the medium. This is not correct: in reality, the MDR accurately takes into account long-range interactions by changing the shape of the contacting bodies36. The MDR, however, considers the sliding process to be quasi-static. While this assumption is satisfied for elastomer friction at velocities much smaller than the velocity of sound, it may not always be valid for dry friction, or for friction in the presence of adhesion42. As was shown in Ref.42, for such systems, the interfacial dynamics may play an important role. For the problem considered in this paper we conclude, however, that the all essential interactions in the medium are correctly taken into account.
References
Persson, B. N. J. Sliding Friction: Physical Principles and Applications. (Springer, Berlin, 2000).
Popov, V. L. Contact Mechanics and Friction: Physical Principles and Applications. (Springer, Berlin, 2010).
Amontons, G. De la resistance cause dans les machines (About Resistance and Force in Machines). Mem. l'Acedemie R. A, 257–282 (1699).
Coulomb, C. A. Theorie des machines simple (theory of simple machines). (Bachelier, Paris, 1821).
Dieterich, J. H. Time Dependent Friction and the Mechanics of Stick-Slip. Pure Appl. Geophys. 116, 790–806 (1978).
Dieterich, J. H. Modeling of rock friction: 1. Experimental results and constitutive equations. J. Geophys. Res. Solid Earth 84, 2161–2168 (1979).
Rice, J. R. & Ruina, A. L. Stability of Steady Frictional Slipping. J. Appl. Mech. 50, 343–349 (1983).
Marone, C. Laboratory-derived friction laws and their application to seismic faulting. Annu. Rev. Earth Planet. Sci. 26, 643–696 (1998).
Dieterich, J. H. & Kilgore, B. D. Direct observation of frictional contacts: New insights for state-dependent properties. Pure Appl. Geophys. 143, 283–30 (1994).
Baumberger, T., Caroli, C., Perrin, B. & Ronsin, O. Nonlinear analysis of the stick-slip bifurcation in the creep-controlled regime of dry friction. Phys. Rev. E. 51, 4005 (1995).
Baumberger, T. Contact dynamics and friction at a solid-solid interface: Material versus statistical aspects. Solid State Commun. 102, 175–185 (1997).
Popov, V. L., Grzemba, B., Starcevic, J. & Popov, M. Rate and state dependent friction laws and the prediction of earthquakes: What can we learn from laboratory models? Tectonophysics 532–535, 291–300 (2012).
Bowden, F. P. & Tabor, D. The Friction and Lubrication of Solids. (Clarendon Press, Oxford, 1986).
Dieterich, J. H. & Kilgore, B. D. Imaging surface contacts: Power law contact distributions and contact stresses in quartz, calcite, glass and acrylic plastic. Tectonophysics 256, 219–239 (1996).
Müser, M. H., Urbakh, M. & Robbins, M. O. Statistical Mechanics of Static and Low-Velocity Kinetic Friction. Adv. Chem. Phys., Ed. by Prigogine, I., Rice, S. A., 126 (2003).
Baumberger, T., Berthoud, P. & Caroli, C. Physical analysis of the state- and rate-dependent friction law. II. Dynamic friction. Phys. Rev. B 60, 3928 (1999).
Ostermeyer, G. P. On the dynamics of the friction coefficient. Wear 254, 852–858 (2003).
Ostermeyer, G. P. & Müller, M. Dynamic interaction of friction and surface topography in brake systems. Tribol. Int. 39, 370–380 (2006).
Popov, V. L. Thermodynamics and kinetics of shear-induced melting of a thin layer of lubricant confined between solids. Tech. Phys. 46, 605–615 (2001).
Heslot, F., Baumberger, T., Perrin, B., Caroli, B. & Caroli, C. Creep, stick-slip and dry-friction dynamics: Experiments and a heuristic model. Phys. Rev. E. 49, 4973 (1994).
Rice, J. R., Lapusta, N. & Ranjith, K. Rate and state dependent friction and the stability of sliding between elastically deformable solids. J. `Mech. Phys. Solids 49, 1865–1898 (2001).
Filippov, A. E. & Popov, V. L. Modified Burridge–Knopoff model with state dependent friction. Tribol. Int. 43, 1392–1399 (2010).
Popov, V. L. A theory of the transition from static to kinetic friction in boundary lubrication layers. Solid State Commun. 115, 369–373 (2000).
Schargott, M. & Popov, V. L. Mechanismen von Stick-Slip- und Losbrech-Instabilitäten. Tribol. und Schmierungstechnik 5, 11–17 (2003).
Canudas de Wit, C. & Ischinsky, P. Adaptive friction compensation with partially known dynamic friction model. Int. J. Adapt. Control Signal Process. 11, 65–80 (1997).
Dupont, P., Hayward, V., Armstrong, B. & Altpeter, F. Single state elastoplastic friction models. IEEE Trans. on, Autom. Control 47, 787–792 (2002).
Lampaert, V., Al-Bender, F. & Swevers, J. Experimental Characterization of Dry Friction at Low Velocities on a Developed Tribometer Setup for Macroscopic Measurements. Tribol. Lett. 16, 95–105 (2004).
Popov, V. L., Starcevic, J. & Filippov, A. E. Influence of Ultrasonic In-Plane Oscillations on Static and Sliding Friction and Intrinsic Length Scale of Dry Friction Processes. Tribol. Lett. 39, 25–30 (2010).
Filippov, A. E. & Popov, V. L. Fractal Tomlinson model for mesoscopic friction: From microscopic velocity-dependent damping to macroscopic Coulomb friction. Phys. Rev. E.2 75, 027103 (7AD).
Greenwood, J. A. & Tabor, D. The friction of hard sliders on lubricated rubber – the importance of deformation losses. Proc. Roy. Soc. 71, 989–1001 (1958).
Grosch, K. A. Relation between Friction and Visco-Elastic Properties of Rubber. Proc. R. Soc. London, Ser. A, Math. Phys. Sci. 274, 21–39 (1963).
Li, Q. et al. Friction between a viscoelastic body and a rigid surface with random self-affine roughness. Phys. Rev. Lett. 111, 034301 (2013).
Heß M. On the reduction method of dimensionality: The exact mapping of axisymmetric contact problems with and without adhesion. Phys. Mesomech. 15, 264–269 (2012).
Pohrt, R., Popov, V. L. & Filippov, A. E. Normal contact stiffness of elastic solids with fractal rough surfaces for one- and three-dimensional systems. Phys. Rev. E. 86, 026710 (2012).
Popov, V. L. Method of reduction of dimensionality in contact and friction mechanics: A linkage between micro and macro scales. Friction 1, 41–62 (2013).
Popov, V. L. & Heß, M. Methode der Dimensionsreduktion in Kontaktmechanik und Reibung(Method of dimensionality reduction in contact mechanics and friction). (Springer-Verlag, Berlin, 2013).
Kürschner, S. & Popov, V. L. Penetration of self-affine fractal rough rigid bodies into a model elastomer having a linear viscous rheology. Phys. Rev. E. 87, 042802 (2013).
Lyashenko, I. A., Pastewka, L. & Persson, B. N. J. Comment on “Friction Between a Viscoelastic Body and a Rigid Surface with Random Self-Affine Surface.”.Phys. Rev. Lett. 111, 189401 (2013).
Li, Q. et al. Li et al. Reply. Phys. Rev. Lett. 111, 189402 (2013).
Scaraggi, M., Putignano, C. & Carbone, G. Elastic contact of rough surfaces: A simple criterion to make 2D isotropic roughness equivalent to 1D one. Wear 297, 811–817 (2013).
Popov, V. L. & Heß, M. Method of Dimensionality Reduction in Contact Mechanics and Friction. (Springer-Verlag, Berlin, 2014).
Braun, O. M., Barel, I. & Urbakh M. Dynamics of Transition from Static to Kinetic Friction. Phys. Rev. Lett. 103, 194301 (2009).
Acknowledgements
This work was supported by the Federal Ministry of Economics and Technology (Germany) under the contract 03EFT9BE55, the Ministry of Education of the Russian Federation and Deutsche Forschungsgemeinschaft (DFG), Q. Li was supported by a scholarship of China Scholarship Council (CSC).
Author information
Authors and Affiliations
Contributions
V.L.P. and S.G.P. conceived the research, Q.L. carried out the numerical simulation, A.D. and M.P. designed the initial program code. V.L.P. and Q.L. discussed the results and contributed to preparing the manuscript. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Li, Q., Dimaki, A., Popov, M. et al. Kinetics of the coefficient of friction of elastomers. Sci Rep 4, 5795 (2014). https://doi.org/10.1038/srep05795
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05795
This article is cited by
-
Scaling theory of rubber sliding friction
Scientific Reports (2021)
-
On the role of scales in contact mechanics and friction between elastomers and randomly rough self-affine surfaces
Scientific Reports (2015)
-
Comment on “Contact Mechanics for Randomly Rough Surfaces: On the Validity of the Method of Reduction of Dimensionality” by Bo Persson in Tribology Letters
Tribology Letters (2015)
-
Contact Mechanics for Randomly Rough Surfaces: On the Validity of the Method of Reduction of Dimensionality
Tribology Letters (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

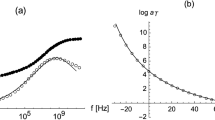






 and
and  as functions of velocity for 20 exponentially increasing normal forces FN from 10−2 to 102 N.
as functions of velocity for 20 exponentially increasing normal forces FN from 10−2 to 102 N.

