Introduction

The security of quantum key distribution (QKD) can be guaranteed based on some mathematical models of the users' devices1,2,3. Unfortunately, the actual devices do not necessarily follow mathematical models and we need to close the gap (side-channel) between the actual device and the mathematical model to implement secure QKD systems in practice. Among side-channels, the side-channel of a photon detector seems to be most easily exploited by an eavesdropper (Eve) since it accepts any input from Eve who can generate an arbitrary optical state such that it causes an unexpected behavior in the detector. In fact, the famous bright-pulse illumination attacks are based on side-channel in detectors4. In order to countermeasure such attacks, measurement-device-independent (MDI) QKD5 was proposed to make BB846 free from any possible side-channel in a detector. We note that MDI QKD for continuous variable was proposed by7,8. In MDI QKD, Alice and Bob do not perform any measurement but only send quantum signals to be measured by Eve. Therefore, bit strings generated by Alice and Bob are free from side-channels in photon detectors since they do not employ photon detectors. Since its invention, MDI QKD has been actively studied both theoretically9,10,11,12 and experimentally13,14,15,16.

As is the case in prepare & measure scheme, implementation of protocols other than BB84 in MDI setting could be suitable for some practical situations. In fact, many experiments for non-BB84 type prepare & measure schemes, including B9217, DPS QKD18, coherent one-way protocol19, SARG0420, etc, have been reported21. Therefore, it is useful in practice to use non-BB84 type protocols in MDI setting and in this paper we consider to use SARG04 protocol in MDI setting, which we refer to as MDI SARG04. SARG04 was originally proposed to make BB84 robust against photon number splitting (PNS) attacks22,23 just by changing the classical post-processing part in BB84. It is proven that SARG04 can indeed generate a key from two-photon emission event by Alice in addition to single-photon emission event24,25, showing robustness against PNS attack in some parameter regimes. Note in MDI setting is that both Alice and Bob are the sender of the signals and as a result, the information leakage from the signals seems to be larger than the one in prepare & measure setting. Therefore, it is not trivial whether both single and two-photon emission events can contribute to the key generation or not. Our work answers this question and we have found that the single-photon emission event by both Alice and Bob, or single-photon and two-photon emission by each of Alice and Bob can contribute to generating a key, but two-photon emission by the two parties cannot make the contribution when a probability of Eve's announcement of the successful measurement for the two-photon emission event is smaller than 1/16.

Another important issue to be addressed in MDI setting is what kind of measurement setup should be implemented experimentally at Eve's laboratory. Naively thinking, as SARG04 differs from BB84 only in the post-processing part, the same measurement setup for MDI BB84 should also work for MDI-SARG04 protocol. On the contrary, however, it turns out that the measurement setup for MDI BB84 results in high bit error rate when applied to MDI-SARG04 protocol and consequently, no significant key can be generated. To generate a key in practice, we propose two alternative measurement schemes for the MDI-SARG04 protocol and simulate the resulting key generation rate.

Results

MDI-SARG04 QKD protocol

In this section, we introduce the MDI-SARG04 QKD protocol. First, we summarize the assumptions and mathematical definitions made in this paper and then we describe how the protocol runs.

Assumptions and definitions

We assume that each of Alice and Bob has a phase randomized photon source, i.e. the vacuum, a single photon and multi photons are emitted probabilistically. The probabilities of the n-photon emission from Alice and Bob are pn and , respectively, which satisfy . We encode the bit information in polarization of photons and we assume that the preparation of the polarization is precise without any flaw. For simplicity, we consider the asymptotic case to neglect any statistical fluctuation, i.e., the number of the signals sent by Alice and Bob is infinite. In our paper, horizontal and vertical polarization states of a single photon are represented by Z-basis qubit states, namely |0z〉 and |1z〉, respectively. We also define X (rectilinear)-basis states as for i = 0, 1. By using a creation operator for a single photon in a polarization θ and the vacuum state |vac〉, we denote an n-photon number state with polarization θ by . (note that when the subscript θ is z or x, it refers to the qubit state rather than the photon number state). Other definitions we use are as follows: |φi〉 = cos(π/8)|0x〉 + (−1)i sin(π/8)|1x〉 for i = 0, 1 and |φi〉 = sin(π/8)|0x〉 + (−1)i−1 cos(π/8)|1x〉 for i = 2, 3. R = exp(−π/2Y), where Y = −i|0z〉〈1z| + i|1z〉〈0z|, which satisfies for all i. and . We denote P(·) = (·)(·).

The protocol of the MDI-SARG04 QKD

The protocol runs as follows:

(a1) Alice and Bob choose a bit value i and i′ (i, i′ = 0, 1), respectively and they encode the bit value into the photonic states of their pulses as and .

(a2) Alice and Bob rotate the polarization of their pulses by applying rotation Rk and with randomly-chosen values of k( = 0, 1, 2, 3) and k′( = 0, 1, 2, 3), respectively, where Rk is defined by Rk ≡ Rk. After the rotation, Alice and Bob send the pulses to Eve's measurement unit (MU) through quantum channels.

(a3) Eve performs a measurement on the incoming pulses and announces to Alice and Bob over the authenticated public channel whether her measurement outcome is successful or not. When the outcome is successful, she also announces types of the successful events, either Type1 or Type2.

(a4) Alice and Bob broadcast k and k′, over the authenticated public channel. If the measurement outcome in (a3) is successful with Type1 and k = k′ = 0, …, 3, they keep their bit values i and i′ in (a1) and Alice flips her bit. If the measurement outcome in (a3) is successful with Type2 and k = k′ = 0, 2, they keep their bit values i and i′ in (a1). In all the other cases, they discard their bit values.

(a5) Alice and Bob repeat from (a1) to (a4) until the number of the successful events with rotation k = k′ = 0, …, 3 in Type1 becomes N1 and k = k′ = 0, 2 in Type2 becomes N2. Let be the number of the successful detection event of Type i. Alice and Bob announce randomly-chosen bits over the authenticated public channel, where ζ is much smaller than 1 and estimate the error rate in the remaining code bits. The estimated number of the bit error in the code bits is denoted by .

(a6) Alice and Bob perform error correction and privacy amplification on the remaining bits by their discussion over the public channel. As a result, they share a final key of length G1N1(1 − ζ) + G2N2(1 − ζ).

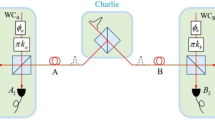
At Eve's MU in (a3), honest Eve performs the Bell measurement in order to establish quantum correlations between Alice and Bob to generate the key. In Fig. 1, the experimental setup for the Bell measurement is depicted. It employs a half beam splitter (BS), two polarization BSs (PBSs) and the photon detectors. In the case where both Alice and Bob emit a single photon, the simultaneous photon detection events matching the pattern Type1 (Type2), listed in Table I, corresponds to the detection of |ψ−〉 (|ψ+〉). We emphasize that in the security proof we assume that Eve is malicious and has a control over the quantum channels and all the bit errors are attributed to the consequence of the eavesdropping.

Table 1 Two types of the successful events announced by Eve's MU. Type1 is the coincidence detection events of or denoted in Fig. 1. Type2 is the coincidence events of or . When the successful events are Type1 and Type2, Alice and Bob distill the states |ψ−〉 and |ψ+〉, respectively, in the virtual protocol.
Full size table
Figure 1
figure 1

Schematic of an experimental setup for the MDI-SARG04 QKD.

The role of Eve's measurement unit (MU) is to perform entangling operation on the photons from Alice and Bob, which is implemented by using a half beamsplitter (BS) followed by polarization BSs (PBSs) and photon detectors. We note that the PBS passes the photons in 45° polarization and reflects the photons in −45° polarization.

Full size image

Limitation of the experimental setup

In prepare & measure setting, the SARG04 protocol is different from the BB84 protocol only in the post-processing part, i.e., no modification is needed in the experimental setup. In the MDI setting, however, the experimental setup for the BB84 protocols5 cannot be directly used in MDI-SARG04 as it induces a high bit error rate and this is a significant qualitative difference of MDI setting from prepare & measure setting, implying that not all the prepare & measure QKD protocols cannot be directly converted to MDI setting. Therefore, we need to consider an alternative experimental scheme for MDI-SARG04. In this section, we first discuss why the setup for MDI-BB84 gives the high bit error rate and then we propose alternative experimental schemes for MDI-SARG04.

For the explanation we denote by F(n,m) the joint probability that Eve receives n and m photons from Alice and Bob, respectively and obtains the successful measurement outcome. Note that while we do not deal with the types of Eve's successful outcomes separately, the following discussion is valid for both types. For simplicity, we neglect all the losses, including those in the quantum channel and the photon detectors and therefore we can also regard F(n,m) as Q(n,m), which is the joint probability that Alice and Bob respectively emit n and m photons and Eve obtains the successful measurement outcome. Like in the MDI-BB84 protocols, we assume that Alice and Bob use a phase randomized weak coherent light whose average photon number is much smaller than 1. Thus, we have for n + m ≥ 3. For simplicity, we assume Eve is honest, namely the bit error rate for n = m = 1 is zero and all photon detectors have unit quantum efficiency and no dark counting. In the following, we show that even with this simplification favorable to Alice and Bob, no significant key is expected. To see this, we consider the bit error rate and the total bit error rate etot is expected to be

where is the bit error probability under the condition that Alice emits n photons and Bob emits m photons and Eve announces the successful outcome. Note that equation (1) holds in both the MDI-BB84 and MDI-SARG04 protocols. It is clear from equation (1) that the bit error is caused by the case where one party emits two photons and the other party emits the vacuum. It is also clear that cannot be zero since the vacuum emission carries no bit information. In the case of MDI-BB84, this event is always discarded from the sifted key and consequently the bit error rate in the key generation basis, i.e., rectilinear basis, is zero. This is so because the two-photon states and , which contribute to the bit values, are orthogonal and they never produce the successful outcomes in Eve's projection measurement for the basis {|0x〉, |1x〉}. Therefore, in the experiment of MDI-BB84, the bit error rate is very small. In the case of MDI-SARG04, however, two states |2φ0〉 and |2φ1〉 consisting bit values are not orthogonal. This means that the two-photon emission contributes to the successful outcome. More precisely, holds from the direct calculation of Note that Q(1,1)/2 ~ Q(2,0) ~ Q(0,2) and etot ~ 0.25 hold for any linear loss transmittance channel. Therefore, we conclude that the use of the phase randomized coherent light source gives no significant key in MDI-SARG04. In order to generate a key in the MDI-SARG04 protocol, Eve's MU or the photon sources should be modified such that the probability of obtaining the successful outcome due to the two photons and the vacuum state is suppressed. In order to suppress the probability, we propose two experimental setups: (i) Eve performs quantum nondemolition (QND) measurement on the two incoming pulses from Alice and Bob just before mixing them as shown in Fig. 2(a). The QND measurement discriminates whether the photon number in the pulse is 0, 1 or more. Eve accepts only the case where n ≤ 1 and m ≤ 1 and discards the other cases with multiple photons. Thanks to the QND measurement, the total bit error rate is suppressed even if the phase randomized coherent light is used as a photon source. (ii) Without the modification of Eve's MU, Alice and Bob replace the phase randomized coherent light by a heralded single photon source based on a spontaneous parametric down-conversion (SPDC) and a threshold photon detector (see Fig. 2(b)). This dramatically reduces the probabilities of the events of (n, m) = (2, 0) and (0, 2). We will show that these setups enable us to generate the key later.

Figure 2
figure 2

Two experimental setups for generating the key in the MDI-SARG04 protocol.

Both setups significantly eliminate the events caused by (n, m) = (2, 0), (0, 2) and other problematic photon number configurations. (a) Eve performs the QND measurements on the pulses from Alice and Bob and she does not perform the interference measurement for n ≥ 2 or m ≥ 2. Eve accepts only when n ≤ 1 and m ≤ 1 are satisfied. (b) A quasi single-photon source used by Alice and Bob, which is composed of the heralded SPDC process. When detector D0 clicks, Alice/Bob sends her/his pulse at the remaining mode to Eve's MU.

Full size image

Security proof

In this section, we discuss the unconditional security proof (i.e., the security proof against most general attacks) of our scheme. The security proof is independent of the specific device models like in Fig. 2, namely it is valid for any Eve's MU and any photon sources of Alice and Bob. Our proof employs the security proof based on the entanglement distillation protocol (EDP)3,26, where the distillation of |ψ−〉 is considered for Type1 and that of |ψ+〉 is considered for Type2. The proposed EDP-based virtual protocol, which is equivalent to the MDI-SARG04 QKD from Eve's viewpoint, runs as follows.

(V1) Alice and Bob prepare , where for Γ = A,B. Here k( = 0, 1, 2, 3) and k′( = 0, 1, 2, 3) are randomly chosen. The probability distribution of the photon number is equal to that of the photon source in the actual protocol. Alice and Bob send the n and m photon states in A2 and B2 to Eve's MU, respectively.

(V2) Eve performs a measurement on the photons coming from Alice and Bob and announces to them whether the measurement is successful (including the type of the event) or not. If the measurement result is not successful, Alice and Bob discard their qubits.

(V3) Alice and Bob broadcast the labels k and k′, respectively. In the cases of k = k′ = 1, 3 with the announcement of Type2 or k ≠ k′, Alice and Bob discard their qubits.

(V4) Alice and Bob repeat (v1) – (v3) many times until the number of the successful events for k = k′ becomes Ni for i = 1, 2, where i corresponds to the type of the events.

(V5) Let be the number of the successful detection event for Type i. Alice and Bob announce randomly chosen -photon pairs over the authenticated public channel, where ζ is much smaller than 1 and then they perform Z-basis measurement on their qubits of the chosen pairs. By sharing their measurement results over the authenticated public channel, they estimate the bit error rate on the code qubits denoted by . As a result, the number of the bit error is estimated to be .

(V6) They estimate the upper bound on the phase error rate for n and m photons from the bit error rate for n and m photons. Here the phase error is defined by the bit error that would have been obtained if they had measured the qubit pairs by X basis, which is the complementarity basis of the computational basis.

(V7) When the bit and the phase errors are smaller than a threshold value for entanglement distillation, they perform the distillation for qubit pairs. For the cases of Type1 and Type2, they distill the photon pairs in states |ψ−〉 and |ψ+〉, respectively. We denote the number of the distilled maximally entangled qubit pairs as GiNi(1 − ζ). Finally, by performing Z-measurements on the distilled photon pairs, they obtain the key.

The important quantities in the proof is the bit and phase errors and the phase error rate determines the amount of privacy amplification. The bit error rate in the code bits of the virtual protocol, which is exactly the same as the one of the actual protocol, is directly estimated by test bits. On the other hand, the phase error rate is defined by the complementary basis X, which Alice and Bob never employ and therefore this rate is not directly estimated in the protocols. Note that we are allowed to work on Alice's n-photon emission and Bob's m-photon emission separately, because Alice's and Bob's photon sources in the protocols are phase randomized. In the following subsections, we present the estimation of the phase error rates for the cases of Type1 and Type2 independently. We derive an upper bound on the phase error for i = 1, 2, where the superscript (1, 1) denotes n = m = 1 and the subscript represents the type of the successful outcome and derive an upper bound on the phase error . We show that in the case of n = m = 2, no key can be generated when the probability of Eve's successful outcome for the two-photon emission event is smaller than 1/16. We note that in the cases of either n ≥ 3 or m ≥ 3, Eve can perform an unambiguous state discrimination to one of the three-photon emission part27,28 and thus we cannot extract the key from such events, given that the channel is lossy enough.

Finally, we note that given the phase error rates, and , the asymptotic key rate for Type i is written by29

Here h(x) = −x log2x − (1 − x) log2(1 − x) is the binary shannon entropy.

phase error estimation for (n, m) = (1, 1) and (1, 2)

By the analysis based on the virtual protocol, we give the phase error estimation formula for (n, m) = (1, 1) and (n, m) = (1, 2). The estimation is performed for Type1 and Type2, separately and we detail the derivation of the phase error estimation in Methods section.

In the case of Type 1, we have

for (n, m) = (1, 1) and

for (n, m) = (1, 2), where

In the case of Type 2, we have

for (n, m) = (1, 1) and

for (n, m) = (1, 2), where g(s2) is the maximal solution of the following equation for x

We depict the dependencies of the phase error rates on the bit error rates in Fig. 3.

Figure 3
figure 3

The relations between the phase error rates and the bit error rates (a) for (n, m) = (1, 1) and (b) for (n, m) = (1, 2).

Full size image

Impossibility of generating a key from n = m = 2

For the case of n = m = 2, the key cannot be obtained for n = m = 2 in Type1 and Type2 by giving an explicit Eve's attack which give a phase error of 0.5, as long as the success probability of Eve's measurement conditioned that both Alice and Bob emit two photons is not larger than 1/16. We show the proof in Methods section. We will prove that we cannot generate a key from n = m = 2 in the virtual protocol and it follows that we cannot generate a key from n = m = 2 in the actual protocol either. To see this, note that the virtual protocol differs from the actual protocol only in the way to prepare the state and the state prepared and post data-processing are exactly the same in both protocols. In other words, only the local operation needed in state-preparation process by the legitimated parties are different in the two protocols. By recalling that any local operation cannot convert a separable state into a non-separable state, we conclude that if we cannot generate a key from a virtual protocol, then we cannot generate a key from the actual protocol.

Simulation

Here we show the results of the key generation rate for the two experimental setups as shown in Figs. 2(a) and (b) by using typical experimental parameters taken from Gobby-Yuan-Shields (GYS) experiment30, where the quantum efficiency and the dark counting of the all detectors in Eve's MU are η = 0.045 and d = 8.5 × 10−7, respectively, the loss coefficient of the quantum channel is ξ = 0.21 dB/km and the inefficiency of the error correcting code is 1.22. In the simulation, we use infinite number of decoy states31 in order to obtain , , and . Assuming that the bit error is stemmed only from dark countings of the detectors, we ignore the other imperfections such as the misalignment of the devices. We also assume that the mean photon numbers of the signal pulses prepared by Alice and Bob are the same and the MU in Eve is the middle of Alice and Bob. The mean photon number for the signal is optimized for maximizing the key generation rate at each distance. By using equation (2) with the above parameters and assumptions, we calculate the key generation rate as a function of the distance between Alice and Bob (i) when Eve postselects the events with n ≤ 1 and m ≤ 1 with the QND measurement as shown in Fig. 2(a) and Alice and Bob use the coherent pulses and (ii) when Eve uses the MU in Fig. 1 and Alice and Bob use quasi single photon sources prepared by the SPDC in Fig. 2(b).

Case (i) – The simulation result of the key rate is shown in Fig. 4(a) and the mean photon number which maximizes the key rate is shown in Fig. 5. We also plot the key rates of Type1 and Type2 separately in Fig. 4(b). The details for obtaining these figures are shown in Supplementary. When the distance is zero, since there is no photon loss before the BS and the multi-photon emissions are excluded, the events of multi-photon input have no contribution to the key rate. In fact, in Fig. 4(a), the two key rates at zero distance obtained from only (n, m) = (1, 1) and from both (n, m) = (1, 1), (1, 2) and (2, 1) are exactly the same. When the distance becomes longer, we see from Fig. 5 that the contribution of the multi photons becomes larger. For the key rate from only (n, m) = (1, 1), the mean photon number is monotonically decrease because the multi-photon emissions give only adverse effect. On the other hand, when we extract the key additionally from the multi photons, the mean photon number does not decrease monotonically, which shows an advantage in using multi-photon emission.

Figure 4
figure 4

The key rate when Alice and Bob use coherent pulses and Eve performs non-destructively exclusion of the multi-photons from Alice and Bob.

(a) Bottom: the key rate of the MDI-SARG04 protocol from (n, m) = (1, 1) only. Middle: the key rate of the MDI-SARG04 protocol from (n, m) = (1, 1), (1, 2) and (2, 1). Top: the key rate of the MDI-BB84 protocol. (b) The upper and lower solid lines are the key rates from (n, m) = (1, 1), (1, 2) and (2, 1) for Type1 and Type2, respectively. The upper and lower dashed lines are the key rates from (n, m) = (1, 1) for Type1 and Type2, respectively.

Full size image
Figure 5
figure 5

The optimal mean photon number for the key rate in Fig. 4.

For the key rates from (n, m) = (1, 1), the three lines show the mean photon number when we consider only Type1, both types and only Type2 from the top. The mean photon numbers for the key rates from (n, m) = (1, 1), (1, 2) and (2, 1) show a similar tendency. The dashed line is for the MDI-BB84 protocol.

Full size image

Case (ii) – Alice and Bob use quasi single photon sources by SPDC as shown in Fig. 2(b). Detector D0 is the same as that used in Eve's MU, namely it is the threshold detector with the quantum efficiency of η = 0.045 and the dark counting of d = 8.5 × 10−7. Eve's MU is the same as that shown in Fig. 1. The key rate is shown in Fig. 6. The details for calculating the key rates are shown in Supplementary. The mean photon number which maximizes the key rate is shown in Fig. 7. From Fig. 6, we see that the key rate only from Type1 and that both from Type1 and Type2 intersect. For the distribution distance longer than the cross point, Type2 has no contribution of the key, which is shown by the blue line in the figure and therefore it is better to generate a key from Type1 only. From Fig. 7, we see that the mean photon number is very small. This is so because the use of larger mean photon numbers results in two-photon emission, which increases the bit error rate. From all the figures of the key rate, one sees that the key rates of MDI-SARG04 are lower than those of MDI-BB84. This tendency holds also for prepare & measure SARG0424,32 and the higher phase error rates of SARG04 protocol than that of BB84 is the main reason of this tendency.

Figure 6
figure 6

The key rate when Alice and Bob use quasi single-photon sources prepared by the SPDC and Eve's MU is the same as the circuit used in the MDI-BB84 protocols.

In this case, the total the key is approximately obtained from only the case of (n, m) = (1, 1) and the successful events of (n, m) = (1, 2) and (n, m) = (2, 1) give little contribution to the key rate. This is so because the probability of the two-photon component in the heralded photon source is negligibly small compared with the probability of the single-photon component. The lines are for MDI-BB84 (black), for both types (red), Type1 (green) and Type2 (blue) of the MDI-SARG04.

Full size image
Figure 7
figure 7

The optimal mean photon number for the key rate in Fig. 6.

The upper line (black) is the mean photon number for the MDI-BB84 protocol. The lower three lines are for the key rates of the MDI-SARG04 protocol obtained from Type1 (green), both types (red) and Type2 (blue) from the top.

Full size image

Discussion

As shown in Figs. 4(a) and 6, the key rates of the MDI-SARG04 protocol are smaller than those of the MDI-BB84 protocol for any distance. This is because the phase error rate of MDI-SARG04 is larger than that of MDI-BB84 and the scaling of all key rates for both protocols linearly depend on the total channel transmittance TAB = TATB between Alice and Bob thanks to an infinite number of decoy states31, where TA(B) is the transmittance between Alice (Bob) and Eve. On the other hand, the scaling of the key rate of MDI-SARG04 can be better than that of MDI-BB84 in a high loss and small error regime when we do not employ the decoy states in the experimental setup in Fig. 2(a), which one can see as follows. For the positive key rate, the joint probability that both of Alice and Bob emit single photons and those photons are detected must be higher than the probability of the emission of the photons satisfying n + m ≥ 4 since Eve causes the detection event preferentially from the multi-photon events such as n + m ≥ 4. Noting that the joint probablity is given by , where μA(B) is the mean photon number of Alice (Bob)'s coherent source, we have , and . These lead to and we see that the scaling of the key rates of MDI-SARG04 is in the order of . By using a similar argument for MDI-BB84, and must hold for the positive key rate, leading to and the scaling of the key rate of . As a result, the key rates of MDI-SARG04 is larger than those of MDI-BB84 in a high loss and small error regime and this is one of the advantage of MDI-SARG04 over MDI-BB84. This tendency is similarly seen in the prepare & measure setting, where the key rates of SARG04 and BB84 scale and , respectively25. Note that implementation of the decoy state method makes the QKD system complicated as it requires the additional amplitude modulation, it increases the amount of classical communications and the software must be modified such that it processes the data depending on whether the pulse is the decoy state or the signal state. Therefore, in some practical situations where simple implementation is preferable, MDI-SARG04 is advantageous over MDI-BB84.

In our analysis, we have considered the asymptotic length of the key. It is interesting to consider the security with finite resources12,33,34. Regarding with the analysis of the decoy state method with finite number of signals, we can directly apply the technique developed for MDI-BB8412 to MDI-SARG04 since the estimation of the yields and the bit error rates of the single/two-photon part in a particular signal/decoy state is totally independent of the protocol that we run and it is solely independent on the intensities of the signal/decoy states. On the other hand, however, the phase error estimation of MDI-SARG04 is essentially different from that of MDI-BB84. In the case of BB84-type protocol, Alice and Bob directly measure both the bit and phase errors in the test bits, which enables them to apply the random sampling theory for the phase error estimation in the code bits. In the case of MDI-SARG04, on the other hand, the phase error is not directly measured and it is estimated via symmetry, i.e., the random rotations and the filtering operation, as well as Azuma's inequality35. Therefore, the phase error estimation is essentially different from the one in BB84-type protocol and we leave it for future works.

In the conclusion, we first proved the unconditional security of the MDI QKD based on the SARG04 protocol. In our security proof, we gave the upper bounds on the phase error rate when Alice and Bob emit single photons and when one party emit one photon and the other half emit two photons. For the case of the two photon emissions from both parties, we proved that a key cannot be generated as long as the probability of success in her measurement conditioned that both Alice and Bob emit two photons is not larger than 1/16. Another important issue to be addressed in MDI setting is what kind of measurement should be implemented experimentally at Eve's laboratory. We have shown that the measurement setup for BB84 in MDI setting cannot be used in SARG04 in MDI setting and we proposed two measurement schemes for MDI SARG04. In the first one, Alice and Bob use heralded single photon sources prepared by SPDC. In the second one, Eve performs QND measurement on the two pulses coming from Alice and Bob individually. In our simulation based on these experimental setups, it was confirmed that these setup can generate a key.

Methods

Proof of the phase error estimation for n = m = 1

Here, we give the phase error estimation for n = m = 1. For this, it is convenient to recall a mathematical property of the maximally entangled state that is satisfied for any operator M. Therefore in (v1) is expressed as , where . Physically, this identification can be interpreted as the situation where |ϕ+〉 is prepared by each of the parties, the filtering operation, of which successful case is described by F1, is applied and then each party sends the photons to Eve only when the filtering operation succeeds (also see Fig. 8). For the simplicity of the security proof, we make an overestimation of Eve's ability in terms of the accessibility of the photons, namely, we imagine Eve who has a direct access to photons of and rather than A2 and B2 and she can prepare any joint state of the photons of and . For later convenience, we denote by the state prepared by Eve.

Figure 8
figure 8

Schematic that is equivalent to the EDP for n = m = 1.

While Eve accesses only the photons in modes A2 and B2 in the actual protocol, we pessimistically suppose that she can prepare any state in and for simplicity of the proof.

Full size image

In the following, we first discuss the case of Type1. We define as the joint probability that the photons in pass through the filtering operation and induces a bit/phase error to the state |ψ−〉 after the rotation. Here and are POVM elements of the bit and phase error measurements on , respectively. The probability that the two photons in pass through the successful filtering operation is described by , where the POVM element of the successful filtering operation on the two photons is

where P(·) = (·)(·). The POVMs for the bit and the phase errors are written as

Applying the Bayes' rule, the bit error rate and the phase error rate in the final state in modes A1 and B1 are described by

The phase error estimation can be established by directly writing down the explicit form of equation (10) comparing each matrix element and one can conclude that

Thus from equations (9) and (11), the phase error rate is precisely estimated, by using the bit error rate, as shown in equation (3). Thanks to Azuma's inequality35, equation (3) holds for any eavesdropping including coherent attacks.

Next, we estimate the phase error rate for Type2. Because only the cases of k = k′ = 0, 2 are accepted for Type2, the definition of the POVM element of the successful filtering operation is changed to

and the probability that the two photons in pass through the successful filtering operation is expressed by . We describe a joint probability that the two photons in pass through the successful filtering operation after the rotation and then the photons in modes A1 and B1 have a bit/phase error to the state |ψ+〉 by . Like in the case of Type1, the POVM elements of and are written by

and

By using the Bayes' rule, the bit/phase error rate of in the final state is expressed by

In order to see the relation between the bit and phase error rates, we consider an inequality to bound the phase error as , where s is a real number, which is equivalent to for . By considering a non-negativity condition of , we see that this inequality always holds when s ≥ 3 and therefore, we have the relation between the phase error rate and the bit error as shown in equation (6).

Proof of the phase error estimation for n = 1 and m = 2

Below, we give the phase error estimation for n = 1 and m = 2. By using the similar argument as n = m = 1, at Bob's side in (v1) is defined by as in Fig. 9, where . Here we note that two-photon emission part is simulated by preparing two pairs of |ϕ+〉 followed by the rotation and the filtering operation on two qubits (see also Fig. 9). In this virtual protocol, while we consider two photons in different modes, this never underestimates Eve's ability. This is so because two photons in the different modes and two photons in a single mode can be converted just by an unitary transformation as . We note that because the photon in mode B3 is in |0x〉 after the filtering operation and it is decoupled from all the other systems, the component is not related to the security proof. Again, we employ the overestimation that Eve has the control over the state of the systems of , and and we denote the three-photon state by , which is prepared by Eve after her announcement of the success. Like in the case for n = m = 1, we estimate a phase error for each case of Type1 and Type2 separately.

Figure 9
figure 9

Schematic which is equivalent to the EDP for n = 1 and m = 2.

By Eve's announcement for the successful measurement on the photons in A2, B2 and B4, the three-photon state is prepared.

Full size image

For Type1, define a POVM element of the successful filtering operations on as

Here the probability of the successful filtering operation is written by . We define as a joint probability that the photons in pass through the filtering operation and induces a bit/phase error to the state |ψ−〉 after the rotation. the successful filtering operation after the rotation is performed on the two photons in and then the photons in modes A1 and B1 have a bit/phase error to the state |ψ−〉. Here, POVM elements of are written by

The actual bit error rate and phase error rate for n = 1 and m = 2 are obtained by accommodating the normalization by and they are expressed as

In order to see the relation between the bit and phase error rates, we consider an inequality to bound the phase error as , where s1 and t1 are real numbers. By using equations (17) – (19) and the linearity of the trace, we obtain an inequality as , which is satisfied when

Therefore the phase error rate is given by using the bit error as shown in equation (4).

For Type2, we define a POVM element of the successful filtering operation by limiting the summation only to k = 0, 2 and by replacing 1/4 with 1/2 in equation (17). The probability of the successful filtering operation is described by . We also define joint probabilities of passing through the filtering and presenting bit and phase errors to the state |ψ+〉 by and . We define the POVM element of by limiting the summation only to k = 0, 2 and replacing 1/4 with 1/2 in equation (18) and that of is defined by limiting the summation only to k = 0, 2, replacing 1/4 with 1/2 and |iz〉 with for mode B1. In a similar manner as the case of Type1 for n = 1 and m = 2, by using the bit error rate defined by , the phase error rate as and real numbers s2 and t2, we consider an inequality as , which leads to . From this inequality, we obtain t2 ≥ g(s2), where g(s2) is the maximal solution of equation (8). Using g(s2), we have the relation between the phase error rate and the bit error as shown in equation (7).

Proof of the impossibility of generating a key from n = m = 2

For the case of n = m = 2, like in the previous subsection, at Alice's side in (v1) is obtained by and at Bob's side is prepared by the same manner. As a result, the virtual protocol for n = m = 2 is equivalent to the successful situation of the filtering operations, which we depict in Fig. 10. We denote the state of Alice's and Bob's four qubits after Eve's successful announcement by . In the following, we prove that the key cannot be obtained for n = m = 2 by giving an explicit Eve's attack, namely we give explicit states of , , and which give a phase error of 0.5. The key ingredient is that while Eve cannot manipulate these four qubits, she conclusively prepare such a state on their qubits by announcing the success of her measurement only when she succeeds an eavesdropping measurement on Eve's photons A2, A4, B2 and B4. This attack gives Eve the perfect information on the bit values when her measurement succeeds.

Figure 10
figure 10

Schematic which is equivalent to the EDP for n = m = 2.

By Eve's announcement for the successful measurement on the photons in A2, A4, B2 and B4, the four-photon state is prepared.

Full size image

For Type1, the probability of the successful filtering operation is expressed by , where

The joint probability, that the filtering operation succeeds and the bit/phase error to the state |ψ−〉 is detected, is expressed by , where

The bit/phase error rate is expressed as . One can confirm by direct calculation that a four-photon state of gives and and another four-photon state , which is orthogonal to , gives and . Therefore, although Eve cannot touch the four modes , , and , Eve can prepare the two states by a projective measurement on the four photons in A2, B2, A4 and B4 as . One sees this fact from the equation , which also implies that the preparation succeeds with a probability of 1/16. Thus a malicious Eve achieves the phase error rate of 0.5 for any bit error rate by distributing these states with a relevant probability. This means that the state in A1 and B1 is separable and it follows that no key can be generated for , where is the probability of Eve's successful detection of Type i conditioned that both Alice and Bob emit two photons.

For Type2, with the same fashion as the case of n = 1 and m = 2, POVM elements for the successful filtering operation and for the bit/phase error are defined by replacing the summation range of k, the prefactor and the proper inversion of the bit value of the projection in equations (21) and (22). We consider the following four orthogonal four-photon states for systems , , and , , and . Each state can be prepared by Eve's projective measurement on the four photons in A2, B2, A4 and B4 with a probability of 1/16. By calculating the error probabilities, we see that mixed states 0.25|ν1〉〈ν1| + 0.75|ν2〉〈ν2| and 0.75|ν3〉〈ν3| + 0.25|ν4〉〈ν4| give and , respectively. Therefore Eve achieves any bit error rate below 0.5 while keeping by distributing the above two mixed states with an appropriate probability. As a result, we conclude that for , the key cannot be obtained.