Introduction

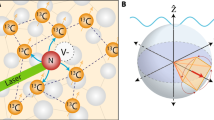
Precision sensing of weak electric and magnetic fields with atomic scale resolution is a pinnacle of measurement science that delivers novel insights and finds immense use from fundamental sciences to biomedical applications. Single Nitrogen-Vacancy (NV) center in diamond is proving to be a sensor of choice for needs that demand high precision measurements and nanoscale spatial resolution. The sensor is atomic sized and could fully operate under ambient conditions and also seamlessly perform measurements at cryogenic and extreme conditions. Nano-scale magnetometry experiments in solids have been demonstrated using single nitrogen-vacancy centres (NV) toward the realization of highly sensitive field sensors operating at room temperature and with atomic resolution (Fig. 1 (a)). The experiments achieved detection sensitivity of very weak magnetic fields (B ≈ 3 nT) with spatial resolution of a few nanometers1,2. These field magnitudes corresponds to those produced by approximately 10 statistically polarized Hydrogen spins at a distance of about 10 nm from the NV defect. These unique prospects of the NV sensors stimulates researchers to develop nanoscale Nuclear Magnetic Resonance and Magnetic Resonant Imaging (NMR/MRI) benefitting structural biology3,4. For realistic applications, like those for NMR, there is an indispensable need to sense multiple frequencies interacting simultaneously with the NV spin. Here we present an efficient method to sense frequency multiplexed signal using a compressed sensing (CS) approach. Further, we show that by employing CS technique we could enhance the precision of the measurement (phase estimation) to scale better with the acquisition time reaching the idealistic Heisenberg limit.

Figure 1
figure 1

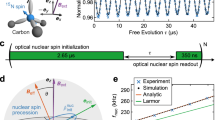
(a) Scheme of NV structure in diamond lattice. (b) Bloch sphere illustration of Larmor precession ϕ(τ) = ωτ around magnetic field ΔB. (c) Top: Original signal given by Larmor precession typically obtained by Ramsey interferometry16. The total time N = 600 determines the dimension of the basis for compressed sensing; (c) Bottom: Recovered signal by compressive sensing after applying a measurement operator A(K × N) using a subset of K = N/2 random data points with a uniform distribution. (d) Top: Discrete Fourier Transform (DFT) of original signal displaying the frequency sparsity of the input. The appearance of a second peak located at N − ω is a numerical effect due to the periodicity of the DFT; (d) Bottom: Recovered signal via compressive sensing in frequency domain.

Full size image

The standard magnetometry protocol using a single NV is as follows. The NV is optically initialized into the ms = 0 state by shining a green laser for about 3 μs. Following this, resonant microwaves makes the spin undergo a state transition from |0〉 ⇒ |−1〉. For sensing alternating external fields the NV spin is put into a superposition state by applying a pulse. The spin precesses along the equatorial plane in a Bloch sphere for a time τ then the spin in flipped by a π pulse and made to undergo the precession in the opposite direction for the same time τ. A non interacting NV spin will not yield any net phase change. If the spin interacts with a time dependent dipole-dipole interaction then there would be some net phase difference. The sensitivity of the quantum sensor is given by the maximum value of the first derivative of phase accumulation with respect to the magnetic field. This quantity is proportional to the interrogation time, which is limited by the NV spin-coherence time and which can be enhanced using isotopically engineered diamond5 or by using dynamical decoupling techniques6. The precision of the technique is given as a measure of its capacity to unambiguously estimate the phase accumulated by an NV spin as a result of the external oscillating field or interactions. In order to find any practical uses pertaining to nanoscale NMR the sensor should have both high sensitivity and good precision to identify closely spaced frequencies. This is very important as we rely on spin signals that are statistically polarized hence novel strategies that could boost the signal-to-noise ratio makes decisive step towards practical application of the diamond sensing technique.

Standard magnetometry precision is limited by statistical fluctuations in the measurements, the so-called Shot-Noise limit 7, where T is the total measurement time required to estimate the magnetic field. This scaling is due to the fact that in a standard measurement n = T/τ independent measurements are performed over a short time-interval τ, yielding a magnetic field precision . Therefore, it should in principle be possible to achieve precision scaling as σB ≈ 1/T, if one were to perform a single measurement over the entire period (τ = T). This is the maximum precision possible for a phase measurement and is referred to as the Heisenberg limit8,9,10. It is very desirable to realize a measurement scheme that follows this Heisenberg limited scaling as SNR of the spin signal is crucial for the nanoscale NMR applications we envision.

Notwidthstanding, there are at least two problems hindering Heisenberg-limited precision in solid state spin magnetometry. The first is spin relaxation which precludes measurements longer than the dephasing time. The second is that performing measurements over long periods usually results in ambiguities. A solution to eliminate the phase-ambiguity problem is the implementation of quantum phase estimation algorithms (QPEAs)11,12. QPEAs are based on applying the inverse Quantum Fourier Transform (QFT)13, which can be implemented using local measurements and control. The problem with just using QPEA is that it produces a probability distribution with large tails, with precision far from the Heisenberg limit. This additional problem can in turn be overcome by applying feedback schemes to achieve 1/T scaling14. A remarkable approach to achieving Heisenberg-like precision scaling based on a phase estimation algorithm (PEA) without adaptive feedback, was proposed in Ref. 15 and successfully implemented in Ref. 16, in combination with single-shot read-out techniques17. In order to prevent ambiguities, the maximum magnetic field range is [−ΔBmax, ΔBmax), which limits the longest accumulation time to:

where the phase accumulation during a Larmor precession can be expressed ϕ(τ) = ωτ, with ω = γB the Zeeman shift (Fig. 1 (b)). PEAs have been applied to several other problems of interest, such as reference-frame alignment18, clock synchronization19, frequency20 and position measurements7, in addition to electric field sensing21. However, a basic conditions for the implementation of PEAs is the assumption that the signal is composed of a single frequency. This can be a significant limiting factor in the presence of temporal fluctuations, or for frequency multiplexed signals where more than one characteristic Larmor frequency may be involved. This scenario is very relevant to nanoscale NMR applications or other involving multiple frequency interactions. In such situation, the standard approach is to repeat n independent Ramsey measurements at equally distributed times (nτ0) up to the dephasing time, thus scaling as .

Motivated by this relevant yet complex scenario, we present an alternative approach for multifrequency magnetometry involving compressive sensing (CS) techniques. CS algorithms are extensively employed in the context of signal processing to recover sparse vectors from a reduced number of measurements. Here sparsity refers to a few non-zero components in a given N-dimensional basis (Fig. 1 (d) top) and the measurement constraints, defined by a suitable measurement operator A, are linear functions of the inputs. When the measurements are chosen at random, the original signal (Fig. 1 (c) top) can be uniquely determined from a small number of measurements (K < N) via efficient convex optimization routines (Fig. 1 (c) bottom and 1 (d) bottom). CS is therefore a highly suitable tool for magnetometry - a sparse problem in frequency - since it satisfies all the above mentioned criteria. CS algorithms have been readily successfully applied to computational biology22 and graphics23, medical imaging24, communication theory25, in addition to quantum state tomography31 and quantum process tomography32 of fairly pure density matrices and low rank quantum operators. As long as the signal is sparse in the frequency domain, sampling using Ramsey scheme provides good reconstruction. Having said this, relaxing the sparsity criteria imposes severe limitations on the validity of the CS reconstruction method. This consequence could be a limiting factor for CS approach in NV-NMR sensing. In order to address this limitations, we propose to use magic angle spinning tailored to the NV sensing experiments3. In this case, spinning the external magnetic field at the magic angle will result in sharper and fewer lines satisfying the sparsity condition for effective CS reconstruction. The goal of the current work is to show how CS techniques could be used efficiently for NV based magnetic sensing. We have demonstrated this using parameters taken from NV based single molecule NMR methods. We choose Glycine molecule because it seems to be an ideal material of choice for first experiments as the NMR spectrum is simple. As a point of reference, we note that there are other competing powerful methods besides compressive sensing, such as super-resolution26,27,28 and filter diagonalization29, which can allow for smoother solutions of the sampling problem and which have proved to be sucessful in the context of NMR information processing, molecular spectroscopy, computational chemestry and computational physics30.

Nitrogen-Vacancy sensors seem to be method of choice for single molecule NMR applications. Our CS scheme presents a method to efficiently sense frequency multiplexed signals using a single NV, which is indeed the case for any realistic magnetic field sensing applications. The NMR signals arising from molecules is complicated and contains chemical-shifts producing mixture of frequencies. The CS scheme described here also paves ways to realize multi-dimensional NMR of organic molecules using single NV defect. We first present our result comparing the CS scheme to the PEA scheme and validate the performance of our CS scheme for sensing single frequencies. Then we proceed to apply the current CS scheme to multifrequency signals resembling realistic case of Glycine molecule and show that CS scheme is suited for performing solid state NMR using diamonds. Furthermore, we show that compressive sensing reconstructions can provide for Heisenberg-like precision scaling, both for the case of single-frequency and multi-frequency magnetometry, thus extending their range of applicability beyond the scope of PEAs, in addition to providing for a 5-fold increase in sensitivity over bandwidth gain as compared with standard measurements. Moreover, we show CS can reduce the total number of resources subject to the complexity of the input signal.

Single-frequency magnetometry via compressive sensing

In order to compare the performance of CS with PEAs in the case of single-frequency magnetometry we consider an analogous Ramsey signal () to the one previously analyzed by Waldherr et al.16 (Fig. 1 (c) Top). We transform this signal to the frequency domain by means of a Discrete Fourier Transform (DFT) algorithm obtaining (Fig. 1 (d) Top), in order to perform random spectral data sampling. We fix the spectral resolution to Δω = 1/N throughout the search, so that all the points in the frequency domain contain information about the full input signal, even though the spectral resolution could be modified adaptively, as discussed below. The maximal detectable frequency is set to 1/τ0, with τ0 given by the upper bound in Eq. (1). The number of sampling points in the frequency domain for the CS algorithms are increased exponentially in the form nk = n02k, where k = 0, 1, …, K (K = 10), with n0 = N/2K, resulting in experimental result vectors , with nk independent elements following Ref. 16. The compressive sensing algorithm is implemented by way of defining A(k,N) (k = 0, …, K) measurement operators consisting of nk random raws of the identity matrix (IN× N) and searching for the most probable vector , which satisfies the measurement constraints . Since A(k,N) is not a square matrix for nk < N, it is non-invertible and the set of linear constraints is underdetermined. The key to the reconstruction is to impose non-linear regularization involving l1-norm minimization33,34. The search can thus be casted into a convex optimization problem of the form:

where we choose a flat distribution as the initial guess (). Numerical results for the output of the convex search are shown in Fig. 2. The phase ϕ(τ) = ωτ is normalized to the Zeeman shift (ω) and is proportional to the time index (τ). Since the phase search is casted into a convex optimization problem, a clear unambiguous peak (i.e., no local maxima) is present even for small number of random sampling points, thus confirming that CS can reduce resource requirements.

Figure 2
figure 2

Typical probability distribution for the estimated phase ϕ via compressive sensing techniques.

Probabilities in different grey tones correspond to increased number of random sample points given by nk = n02k, with k = 0, 1, …, 10. Since the phase search is casted into a convex optimization problem there is no ambiguity (i.e., no local maxima) for a sufficient number of measurements.

Full size image

We are interested in the scaling of the variance () of the estimated vector on the total measurement time (T), corresponding to the square of the magnetic field sensitivity defined as 16. Where the variance is defined as the square of the norm-2 between the estimated vector () and the vector of experimental results (), i.e., . Numerical results for the scaling of precision () vs. total number of resources (T) and for the dependence of sensitivity vs. dynamic range 1/τ0 are displayed in Fig. 3. Figure 3 (a) shows the Heisenberg limit (black line) and a fit to the numerical points obtained via CS, revealing Heisenberg-like scaling ≈ 1/T for phase estimation via CS techniques. Red dots correspond to the Shot-Noise limit (1/T0.5), set by the variance in the standard measurement. CS gives a maximum precision gain as compared to the standard measurement for k = 7, which represents less than 16% of the total resources (N = 600). The number of resources required for a maximum precision gain could be further reduced by means of adaptive techniques, as discussed below. The dependence of the total number of resources on the sharpness of the signal remains to be inspected. The overhead in Fig. 3 (a) is determined by the tolerance of the l1-norm minimization35. We note that the absolute precision yielded by the CS inversion is somewhat arbitrary, we are therefore interested in the scaling of the precision with the total number of resources. Figure 3 (b) displays the sensitivity (δB) of the recovered phase via CS (red dots), for different maximum frequency over magnetic field values (i.e., dynamic range 1/τ0) obtained by increasing ΔBmax, such that τ0 = 0.036, 0.072, 0.144, 0.288, 0.576. The selected range of τ0 permits to increase the dynamic range by 4 bits (from K = 10 to K = 14). This is compared with the standard measurement scheme (black rhombus) showing a 5-fold increase in sensitivity over dynamic range gain, via CS data recovery. We note that the main advantage of our approach is the increase in dynamic range (i.e. bandwidth) without loss of sensitivity, as readily expalined in detail in previous works16. The results presented in Fig. 2 and Fig. 3 confirm that CS techniques can provide for a similar performance as compared with PEAs16, for a reduced number of resources (i.e., total measurement data points) for the case of single-frequency signals. Below we present an application of CS techniques in situations where PEAs are not applicable.

Figure 3
figure 3

(a) Precision scaling () of phase estimation via compressive sensing (CS) vs. total time resources (T). The black line indicates the Heisenberg limit (1/T). Red dots indicate the Shot-Noise limit () given by the standard measurement. The numerical data is fitted to ≈ 1/T (blue line) showing that CS can provide for Heisenberg-like scaling. The overhead is set by the tolerance in the l1-norm minimization. Precision gain over standard measurement using compressive sensing is maximal for k = 7. (b) Dependence of sensitivity (δB) vs. maximal frequency over magnetic field (1/τ0) for the standard measurement (black rombos) as compared to CS approach (red dots). The area between the curves indicates the gain in sensitivity over dynamic range, showing a 5-fold increase with respect to standard measurements.

Full size image

NMR signal - frequency multiplexed magnetometry via compressive sensing

We now present the main result of the paper which consists of applying CS recovery techniques to frequency multiplexed signals. Frequency multiplexed magnetometry can be considered as a very simple case of waveform estimation. In our simple example we only reconstruct two fixed parameters (i.e., two frequencies) but arbitrary waveforms with time-dependent parameters can also be efficiently reconstructed in the context of quantum metrology36. Frequency multiplexed magnetometry can arise, for instance, when the NV sensor is coupled to a spin bath, so that hyperfine coupling results in different Zeeman splittings and different frequencies for Larmor precessions, thus resulting in effective nutations. This scenario is clearly prohibitive for the use of PEAs, however it is clearly amenable for the use of CS approaches. We note that significant literature exists on CS techniques linked to NMR37,38,39. The main novelty of this work is the use of CS approaches for high-bandwith presicion magnetometry in the case multifrequency signals. In order to present a realistic example of frequency-multiplexed signals, we consider the solid state NMR spectrum of a simple amino-acid Glycine molecule. The 13C spins of α-Carbon and the carboxyl group contributes to homo-nuclear dipolar interactions. In a typical solid state spectrum the anisotropic interactions cause significant broadening masking the features. In order to revive the isotropic spectral features the sample is spun at an angle of 54.7 degrees to the external magnetic field to perform Magic Angle Spinning (MAS)40. In this example we have chosen data corresponding to Glycine MAS spectrum at 20 kHz, this condition gives two distinct peaks separated by about 10 kHz41, whose magnetization is given by the sum of two Fourier components with Zeeman splitting Δω = ω1 − ω2 = 10 kHz41, of the explicit form , with N = 1000 (Fig. 4 (a)).

Figure 4
figure 4

(a) Simulated frequency multiplexed signal for 13C-Glycine molecule consisting of Larmor precessions given by two Zeeman shifts ω1,2, with Zeeman splitting Δω = ω1 − ω2 = 10 kHz41 and N = 1000 points. (b) Typical probability distribution for multiple phase estimation, different tones correspond to increased number of random sample points given by nk = n02k, with k = 0, 1, …, 10. (c) Precision scaling () vs. total time resources (T). The precision using CS scales as ≈ 1/T0.8 (blue line). The Heisenberg limit (1/T) is indicated with a black solid line. Red dots correspond to the Shot-Noise limit (1/T0.5) set by the standard measurement. Maximum precision gain via CS reconstruction is obtained for k = 6.

Full size image

Moreover, we consider the same amplitude and off-set phase for the two Fourier components, although this is not a necessary requirement. Indeed, CS can also be used to determine the unknown amplitude relation and off-set phase of the components. We increase the number of random sample data points in the same exponential manner nk = n02k with k = 0, 1, …, 10, keeping (1/τ0) fixed. The recovered phase for different values of k is shown in Fig. 4 (b), displaying two unambiguous peaks, corresponding to the multiple Larmor frequencies ω1,2 even for small number of random sampling points, thus confirming that CS can reduce resource requirements also for signals consisting of multiple frequencies.

Figure 4 (c) shows the precision scaling () vs. total time resources (T) for CS data inversion in the case of frequency multiplexed signals. The numerical data points are fit to ≈ 1/T0.8, with a precision overhead given by the tolerance in the l1-norm minimization algorithm. The Heisenberg limit is indicated with a black line. Red dots correspond to the Shot-Noise limit (1/T0.5), set by the variance in the standard measurement. Even though the precision scaling is slightly lower in the frequency-multiplexed case, the overhead is also reduced under the assumption of ideal measurements, showing that CS techniques can outperform standard measurements even for the smallest number of resources. Furthermore, CS gives a maximum precision gain as compared to the standard measurement for k = 6, which represents less than 10% of the total resources (N = 1000). The number of resources required for a maximum precision gain could be further reduced by means of adaptive techniques, as discussed below. We stress that in this approach we only consider the waveform reconstruction error, without considering the error in estimating the result at each step. The latter error should scale at the Standard Quantum Limit. In this realization we considered a fixed spectral resolution Δω = 1/N throughout the convex search, such that each point in the frequency domain contains information about the full signal in the time domain. As a future step we will consider hybrid approaches, by increasing adaptively the spectral resolution Δωk, starting the search with a broad distribution (Δωk= 0 > 1/N) and narrowing down the frequency window iteratively, while increasing the number of sample points (k). Other relevant hybrid approaches could be implemented by combining structured random measurement operators31.

Conclusions

We reported on a novel approach to frequency multiplexed magnetometry via compressive sensing (CS) techniques. We numerically showed that CS data recovery can provide for Heisenberg-like precision scaling (≈1/T) in situations where phase estimation algorithms (PEAs) are not applicable, in addition to providing for a 5-fold increase in sensitivity over dynamic-range gain and a reduction in the total time-resource requirements, subject to the complexity of the input signal. In our example, we considered a simple sum of a few Fourier components. A less favourable scaling is to be expected for more complex waveforms, with increased number of independent parameters. Moreover, since non-adptive CS uses random sampling the signal recovery is probabilistic and the success rate becomes exponentially smaller for fewer data points. Nevertheless, this limitation can be overcome be means of adaptive sampling techniques. Our results pave the way for potential applications of CS in efficient quantum parameter estimation, quantum sensing and magnetometry involving time-varying42 and frequency multiplexed signals. In particular the reported CS technique paves efficient ways to achieve sensitive NMR detection of solid samples at nanoscale volume and even perform multidimensional spectrum of biomolecules.