Introduction

In classical physics it is possible, in principle, to detect the state of a single system, for example the position and momentum of a point particle, transmit the information about that state to a remote location and then reconstruct it within a second system. This concept of “classical teleportation” underlies telecommunication techniques such as the transfer of documents via facsimile. Quantum physics, however, excludes the possibility to detect or duplicate the state of a single microscopic system1 and therefore rules out all forms of classical teleportation with atoms, photons or other quantum systems. It is thus surprising2, that the state transfer between quantum systems can nevertheless be realized according to the rules of quantum physics by means of “quantum teleportation”3. This procedure makes use of correlations between quantum systems - entanglement - which cannot be described by local-realistic theories4, such as classical mechanics or electrodynamics, nor any other theory within classical physics.

Quantum teleportation lies at the core of quantum communication, which is the quantum analog of telecommunication and can also be employed to enhance the success probability in quantum computing with photons5,6,7,8. Moreover, it is one of the crucial ingredients9,10 for enabling long-distance quantum cryptography - a technique to transmit information secured against eavesdropping.

The importance of quantum teleportation for quantum information processing and communication can be seen from the long list of experimental realizations of teleportation of the state of a two-level system corresponding to the smallest unit of quantum information - one quantum bit (qubit)11,12,13,14,15,16,17,18,19,20,21,22,23. In these realizations single qubits were encoded in the polarization of photons or in the superposition of vacuum and one photon states21. Quantum teleportation with two-level atoms has been demonstrated24,25,26 and it has also been designed for three- and four-level atomic systems27,28.

A way to identify quantum communication channels with high capacity (bandwidth), is to employ multi-level quantum systems that carry superpositions of an arbitrary number d of basis states – qudits – instead of sending many single qubits. Due to their additional parameters, these systems might be optimized against the influence of external noise, such as decoherence of photonic states in turbulent atmosphere29. Moreover, it might save resources. For example, Quantum Key Distribution (QKD) schemes using photonic qudits can securely transmit more than one bit of information per photon30. In order to achieve long-range QKD or quantum communication networks, so-called quantum repeaters9 that teleport qudits are obligatory. Instead of qudits one could teleport multiple qubits, but at the cost of additional transcription of qudits to qubits. While in theory the generalization of teleportation from qubits to qudits is known (cp. for example31,32,33,34,35), the experimental realization of qudit teleportation is a difficult task and has not yet been achieved.

At present, light is the only candidate for quantum communication and quantum cryptography over large distances because of its small interaction with its environment as compared to matter. The maximal distance for quantum communication achieved with photons so far is 144 km through the atmosphere36 limited mainly by absorption. Much further distances seem only possible using teleportation of entangled photons in conjunction with quantum repeaters. At the same time, the small interaction of photons makes it difficult to manipulate the states of light in order to achieve teleportation. There are two main challenges in realizing teleportation: (i) photons sharing maximal quantum correlations (entanglement) have to be generated and distributed between the sender and the receiver of quantum information and (ii) the input photons and the photons of the sender have to be projected into a maximally entangled state by a joint measurement of both (a so-called Bell measurement) in order to transfer the state of the input photons to the photons held by the receiver. Both challenges can in principle be overcome using non-linear optical media, which manipulate the light depending on its intensity. The corresponding processes, however, have a very small efficiency on the single photon level. For example, in spontaneous parametric down-conversion, an incoming pump photon is converted into a pair of entangled photons [challenge (i)], with a probability of 10−6 per incoming photon37. The efficiency of a Bell measurement by means of non-linear optics [challenge (ii)] is even lower17, at about 10−10. Therefore it is desirable to design a more efficient solution to both challenges based on linear optics – i.e. beam splitters, phase shifters, mirrors, etc. Such an efficient solution is presented in this article for the teleportation of the quantum information carried by an arbitrary number d of photonic levels. A different solution to challenge(ii) for qutrits (d = 3) can be found in38. An alternative teleportation scheme for general qudits based on quantum scissors together with a comparison to the present scheme is reported in39.

Although linear optics does not allow the realization of a complete Bell measurement40, a simple 50:50 beam splitter can be used as a filter to project two incoming photons onto a particular entangled state in a certain percentage of the cases. Two photons incident on the input ports of a beam splitter do not produce a coincidence count in two detectors in the output ports (Hong-Ou-Mandel effect41,42) unless they possess an anti-symmetric component with respect to their internal degree of freedom, e.g. their polarization. A coincidence count thus effectively projects onto an antisymmetric state. For two polarized photons entering in different input ports of the beam splitter there is only one such state:

i.e. elementary excitations of the first and second spatial mode (represented by the first and second slot in the state symbol) carrying horizontal and vertical polarization, respectively, superposed with excitations of these modes with swapped polarizations. This state is antisymmetric, because it changes sign under a permutation of the first and second mode (slot) and it is maximally entangled, a condition that allows the realization of the teleportation of a qubit11 encoded in the polarization of a single photon. Moreover, as we shall see in the following, this phenomenon can also be employed for the simultaneous teleportation of multiple qubits encoded in the orbital angular momentum (OAM) of photons.

It was noticed by Allen et al.43 in 1992 that light with a phase distribution exp(ilϕ) depending on the azimuthal angle ϕ in the plane orthogonal to its direction of propagation carries an orbital angular momentum of an integer l times Planck's constant per photon. Such optical beams are characterized by helical (screw-like) wavefronts (see Fig. 1) and can be produced with the aid of spatial light modulators (SLMs) – thin liquid crystal displays. The SLM modulates the optical beam with a helical phase pattern. The orbital angular momentum of a photon can thus be used to carry information and represents a quantum system with an unrestricted number of levels.

Figure 1
figure 1

Schematic diagram of the helical wavefront of a light beam.

Full size image

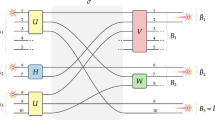
Quantum teleportation using an incomplete Bell measurement (a “Bell filter”) can be applied to systems with an arbitrary number of levels, not only simple two-level systems (such as polarized photons). Let us review how. Teleportation involves three parties Alice, Bob and Charlie, cp. Fig. 2. Alice and Bob are far apart and share a pair of systems in a maximally entangled state

which is a superposition of products of orthogonal basis states of their D-level systems A and B. Charlie provides Alice with an unknown state |χ〉, which has to be transferred from Charlie's system C to Bob's system B. For this purpose systems C and B must be similar - B has to support the same states as C. The state to be teleported can thus be expressed as a superposition of Bob's basis states: . Alice successfully teleports the state |χ〉 if she carries out a measurement that acts like a filter and projects systems C and A onto the entangled state |Ψ〉:

According to the rules of quantum mechanics the likelihood for such a projection to occur is given by the square of the length of the resulting state vector, p = 1/D2. Thus the success probability of this teleportation scheme, which uses only one of the outcomes of a Bell measurement, decreases with the number D of basis states in which quantum information is encoded. The advantage lies in the fact that this concept of teleportation, which is used for photonic qubits (D = 2) can be generalised to teleport states with arbitrary D using linear optics. (For an alternative approach based on quantum scissors47 that uses entanglement contained in single-photon states see39).

Figure 2
figure 2

Teleportation using a filter: source Sψ produces a pair of systems A and B in state |Ψ〉.

System A and system C are to be projected by a filter Fψ into state |Ψ〉. If successful, the filtering transfers the initial state of C to system B.

Full size image

Results

To generalize the qubit scheme to a method that is able to teleport superpositions of multiple basis states, we have to identify a photonic system with a unique antisymmetric state and a linear optical device that plays the role of the beam splitter in the qubit case, i.e. a filter for antisymmetric states. The uniqueness is required to guarantee that the filter yields the same state |Ψ〉CA that is initially shared by Alice and Bob, i.e. the state |Ψ〉AB. The dimension of the space spanned by the antisymmetric states of composite systems (only if the dimension equals 1 do we have a unique antisymmetric state!) can be easily determined by means of Young tableaux (see Methods). It turns out that only d systems each with d levels posses a unique antisymmetric state. As a consequence, a generalization of the teleportation scheme for photonic qubits by means of a Bell filter for antisymmetric states requires d photons propagating on different paths each with a quantized degree of freedom, such as OAM with d-levels. In other words, the generalization requires d qudits.

Photonic states can be conveniently expressed by means of creation operators a† acting on the vacuum state |0〉. In our case these operators carry two indices – the first one, j, specifies one of d possible propagation paths whereas the second one, l = 1 … d, denotes the OAM value of the photon. For example, the state of two photons propagating on different paths with two OAM values l = 1, 2 – which is the OAM analog of the antisymmetric polarization state (1) used in qubit teleportation11 – can be written by means of a determinant of creation operators:

It is obvious that the state |ψ〉 is antisymmetric, since under permutation of the propagation paths it is transferred to −|ψ〉. The antisymmetry is represented by the determinant: a swap of rows corresponding to the permutation results in a minus sign of the determinant. Using the same logic, one can show that the antisymmetric state of d photons with d OAM values can be expressed by the determinant of a d × d matrix Λ

where

Here |Ψ〉 is the required antisymmetric state. The antisymmetry follows from the fact that permutation of any two propagation directions corresponding to a swap of two rows of the determinant in Eq. (5) leads to a change of sign of the state |Ψ〉.

For teleportation the d photons in the antisymmetric state given in Eq. (5) must be divided between Alice (n photons) and Bob (d − n photons) such that both share a bipartite maximally entangled state. To check for maximal entanglement we take advantage of the representation of |Ψ〉 in terms of a determinant. Expanding the determinant with respect to the first row, we obtain the state:

where and Λ1i is the (d − 1) × (d − 1) submatrix obtained by omitting the i-th column and the first row (a so-called minor of Λ) and . It is remarkable that the expansion of the determinant results in a maximally entangled bipartite state of the form (2) with D = d and |Bi〉 = |i〉, implying that Alice and Bob obtain d − 1 and one photon, respectively. This partitioning of photons allows Alice to teleport any state of a single d-level photon from Charlie by sending it along with her d − 1 photons into the beam splitter array depicted in Fig. 3 and subsequently obtaining a coincidence count in all its output ports. The coincidence count results effectively in a projection into the antisymmetric state |Ψ〉 as can be checked for any finite dimension d by direct calculation. On the other hand, the antisymmetric state entering the beam splitter array yields, with certainty, a coincidence count (cp. Methods).

Figure 3
figure 3

Bell filter: an array of d beam splitters (with indicated transmitivities) projects Charlie's incoming photon and Alice's d − 1 photons into the antisymmetric state |Ψ〉 in case of a coincidence count in all detectors.

For this purpose Alice's photons must be already in an antisymmetric state before the projection. To take care of the change of sign of OAM values upon reflection at the beam splitters, the OAM values carried by the light in the horizontal path must have opposite sign to those in the vertical paths.

Full size image

But this is not the only possible partitioning of photons that leads to a maximally entangled state between Alice and Bob. Strikingly, any partition (n, d − n) with 0 < n < d of an antisymmetric state of d particles possesses this property and this can be easily understood by virtue of the rules to calculate determinants (see Methods). For the partition (n, d − n) one obtains a bipartite state as given in Eq. (2) with and |Ai〉 as well as |Bi〉 given in terms of minors of Λ. The maximum amount of quantum information is teleported with a (d/2, d/2) partition of an even number d of photons prepared in state |Ψ〉. In this case Charlie has to provide d/2 photons, cp. Fig. 4 and can send for large d approximately d qubits, simultaneously (cp. Fig. 5). This information is encoded in the dimensional, anti-symmetric subspace spanned by the |Bi〉. This is an exponential gain compared to the teleportation of a single qudit (corresponding to log2(d) qubits) carried by one photon, which requires the same entanglement resource – an antisymmetric state of d photons |Ψ〉. (Note that Charlie's photons must be in an antisymmetric state to guarantee that the beam splitter array acts as a Bell filter in case of a coincidence count in its output ports. A general Bell filter for n photons from Alice and d − n photons from Charlie in antisymmetric states can be constructed by the recursive use of the Bell filter depicted in Fig. 4 combined with heralding techniques for single photons, cp. Fig. 6. An example of a Bell-filter without heralding techniques for qutrits is discussed together with the preparation of a totally antisymmetric state in Methods.). Let us emphasize that this method thus constitutes a simultaneous teleportation of the collective state of several photons.

Figure 4
figure 4

Teleportation of the collective antisymmetric state |χ〉 of d − n photons (number of photons indicated).

Full size image
Figure 5
figure 5

The graphs show the number of quantum information units (qubits) teleported per additional photon versus the number of additional photons required for individual-qubit teleportation (red) and the optimal new technique (blue).

Full size image
Figure 6
figure 6

A general scheme to project into and thus prepare a d-photon totally antisymmetric state.

In this scheme an array of beam-splitters (with indicated reflectivity) is used in a pyramidal structure. Each arm (turquoise box) consists of a Bell-filter as depicted in Fig. 3 of the main text and is followed by an array of single-photon heralding devices in each path. A d-fold coincidence count in the output modes will ensure a projection on the antisymmetric state.

Full size image

Discussion

In comparison, teleporting d qubits individually, one requires the same number of maximally entangled photon pairs, i.e. a total of 2d additional photons, resulting in an efficiency of sending half a qubit per additional photon or 1/3 of a qubit per photon generated. Our scheme yields double these rates and thus requires half the number of photons (cp Fig. (5)) to teleport the same amount of quantum information. This is an important improvement since the number of photons, that can be generated per time-unit is the limiting factor for the bandwidth of photonic quantum communication. However, it holds only for the selective regime conditioned on successful teleportation events. On average the number of photons increases by a factor D2 with the number D = dd of outcomes of a Bell measurement of d qudit photons. Since it might be possible to create Bell filters by means of linear optics for half of the Bell states (cp.40) instead of a single filter as in our case, this would mean an increase of only a factor 2. This is a promising subject for future research since for individual qubit teleportation with linear optics the success probability is limited by 1/2d, resulting in a relative exponential overhead.

In the foregoing presentation of results we assumed the existence of a source SΨ that produces the state |Ψ〉 initially shared by Alice and Bob (cp. challenge (i)) which is treated in the Methods. Indeed for qutrits, such a source can be realized by an additional beam splitter array with two beam splitters (cp. Fig. 3 for d = 3), that acts as a Bell-filter for the antisymmetric state |Ψ〉. For this purpose a single photon together with an antisymmetric state of two photons must enter the array and one photon must leave each of its output ports. In the general case nondestructive heralding techniques based on non-linear optical effects44 might be employed in conjunction with photonic multiports, which however reduce the efficiency of the teleportation scheme. These methods will be discussed elsewhere.

Apart from an additional overhead of photonic resources needed if filtering techniques are used to prepare the antisymmetric state (cp. first paragraph in this section) there is the need to produce simultaneously the number of photons required for the entangled state and the state that carries the quantum information to be teleported. If the photons are generated by single photon sources, the success probabilities for the single photons will multiply and lead to an exponential decrease of the total success probability. This is a serious problem, however, it is also encountered when qubits in an unknown state that cannot be resent are to be teleported individually. To solve this problem one requires techniques investigated for long distance quantum communication and require to store the required number of photons in quantum memories and release them collectively to produce the entangled states needed for the teleportation of complex states.

Methods

Dimension of the antisymmetric subspace

The dimension of an antisymmetric subspace can be calculated using combinatorial objects called Young tableaux, which provide a technique of keeping track of the constraints imposed by the permutation symmetry of the system. Here we represent a basis state of a system by a box, , where a numbers the basis state. A basis of the symmetric combinations of two systems can be depicted by a row of two boxes, . Similarly, a basis of antisymmetric states is represented by a column of boxes, . Since we are interested only in the antisymmetric part, we focus on columns only. The dimension of the corresponding subspace, i.e. the number of basis states, is obtained by counting the different possible ways to fill the boxes with numbers according to certain rules. For the antisymmetric subspace we start filling the numbers in descending order, from top to bottom. For a system that consists of two subsystems, a Young tableaux reads:

where a is always greater than b. Therefore, if the total number of basis states available for each subsystem is two, i.e. we are dealing with two qubits, there is only one possibility, namely a = 2 and b = 1. As a result, we obtain an antisymmetric subspace of dimension one. If the available states are more than two, say d, then we have d − 1 options for a and given a, a − 1 options for b. As a result the total number of combinations is given by 1 + 2 + … + d − 1 = d(d − 1)/2, which is the dimension of the antisymmetric subspace for a pair of d-level systems, each of which can carry one qudit of quantum information.

This can be generalized for systems with n subsystems. Now we have n numbers in a column of boxes. The dimension of this antisymmetric subspace is given by the binomial coefficient , i.e. d choose n, where n is the number of sub-systems. This equals 1 only when n = d, giving us a unique antisymmetric state for d qudits.

Laplace expansion for the determinant of a matrix

The determinant of a n × n matrix A with elements aij can be calculated by an expansion with respect to the first row of A as follows:

Here det(A1i) is the determinant of the (n − 1) × (n − 1) submatrix of A obtained from eliminating the first row and i-th column. In fact this is just a special case of a simultaneous expansion of the determinant with respect to several rows. For example, expanding with respect to the first two rows of a 4 × 4 matrix A, we obtain:

where each block on the right-hand side represents the product of the determinant of the submatrix (minor) with blue dot and the minor with the red dot. In general, any such Laplace expansion assumes the form , where ci = ±1 and the Ai (Bi) are minors of A which differ at least in one column45. The possible Laplace expansions of det Λ in Eq. (4) correspond to the different distributions of the d photons between Alice and Bob. Each distribution leads to orthogonal states |Ai〉 ∝ det(Ai)|0〉 on Alice's side and on Bob's side accordingly and therefore to a maximally entangled state shared between both parties.

Proof of Bell Filter projection onto the antisymmetric state

The goal of this section is to prove that the Bell filter depicted in Fig. (3) projects onto the totally antisymmetric state of d photons upon simultaneous detection in all d detectors of the filter. We assume that the input is given by the combined state of Alice's d − 1 photons, which are in an antisymmetric state and Charlie's single photon. We will consider all the possible states obeying this assumption and show that only the totally antisymmetric state results in a coincidence count. We assume in the following that Charlie's single photon is prepared as a superposition of basis states with the same modulus of OAM values as used to span the Hilbert space for Alice's photons, but with different signs: for i = 1 … d. With this sign convention we can ignore the effect of sign change of the OAM modes (l → −l) upon reflection on a beam splitter or mirror.

Note that d − 1 photons each with d levels form a d-dimensional antisymmetric subspace of the dd−1-dimensional Hilbert space. Therefore, the effective dimension of the allowed state space for Alice's d − 1 photons is the same as the dimension of Charlie's Hilbert space which corresponds to a single photon with d levels.

The general quantum teleportation protocol for d-level systems rests on the complete projective measurement in the maximally entangled generalized Bell basis , which can be defined as:

where and ω = exp(2πinm1/d). For m1 = m2 = 0 we retrieve the state |Ψ〉AB defined in Eq. (2).

Since Alice's system is assumed to be described by the d-dimensional antisymmetric subspace of d − 1 photons, the basis for Alice's system {|Ai〉} can be written as:

where det(Λdi) are the minors of the matrix Λ (cp. Eq. (6)) with respect to the last row. Similarly we can define the basis for Charlie's system. The index i represents the different OAM modes of the single photon. In this notation the states read:

Here Co(Λ)[di] = (−1)i det(Λdi) is the [di]th cofactor of the matrix Λ.

The action of a d-input-d-output beam splitter setup, such as the Bell filter (cp. Fig. (3)), can be represented by a unitary matrix U that transforms the matrix Λ as . After passing through the beam splitter setup, the state transforms to :

Since , we can use the following identity:

and rewrite Eq. (14) as:

We are interested only in those terms in the state that have exactly one photon in each of the output ports and thus may lead to a coincidence count. Note that among the two indices of the creation operator the first index k represents the spatial mode and the second index j stands for the OAM mode. Furthermore, Co(Λ)[lj] does not contain any creation operator in the spatial mode l. Therefore, the terms in the state where k = l contain exactly one photon in each spatial mode and hence may result in a coincidence count. After projecting the state on the subspace of states that correspond to coincidence counts we get an unnormalized state given by:

In the above expression, if we choose

i.e. ηdk ≡ η to be k independent then the expression reads:

which is zero unless m1 = m2 = 0. Therefore, the requirement that η is k independent, is a sufficient condition for a beam splitter setup to project to non-coincidence count states.

Now we can prove that the unitary matrix Ud corresponding to the Bell-Filter in Fig. (3) satisfies Eq. (18). We can write the Ud corresponding to d − 1 beam-splitters as the product of Sd, the matrix for the 1/d:(d − 1)/d beam-splitter and , which corresponds to the rest of the setup. Therefore,

The sufficiency condition (18) then reads:

From Eq. (20) we have:

Substituting (23) in (22), we get:

It is easy to see that

Therefore, when i = 1 then only and survives resulting in ηdi = 1/d. When i ≠ 1, then and are zero. Thus, the only term in Eq. (24) which survives is . Here we used the relation (Ud−1)d−1 i−1Co(Ud−1)[d−1 i−1] = 1/(d − 1) which is assumed to hold for Bell-filter with d − 2 beam-splitters.

State preparation

A general scheme to prepare (project into) an antisymmetric state of d photons can be realized by an array of beam splitters together with non-linear optical devices44,46 that suppress the two- and higher-photon component in a path (cp. Fig. 6). The scheme makes repeated use of the Bell-filter shown in Fig. 3 in the main text. The latter can map the (n − 1)-photon antisymmetric state to the n-photon antisymmetric state with the help of an additional photon in the case of n-fold coincidence counts in its output ports. Hence, if the output of the Bell-filter can be monitored to ensure that only one photon comes out of each of the output port, then this output can be fed to another such setup to generate an (n + 1)-photon antisymmetric state. Therefore, one can generate a d-photon totally-antisymmetric state, recursively, from a product state of d photons.

To prepare the totally antisymmetric state of three photonic qutrits (three-level systems) a single Bell-filter (cp. Fig. 3) that consists of two beam splitters suffices. This requires as input a pair of photons in an antisymmetric state |ψ〉 = |12〉 − |21〉 and a single photon in state |3〉. In addition, one needs to confirm that one photon leaves each output port. This can be achieved without single-photon heralding by sending two photons from different output ports to Bob who confirms this by a state tomography and one photon to Alice together with a photon pair from Charlie. A subsequent three-fold coincidence count after Alice's Bell filter (a copy of the one used for preparation) then announces successful state preparation as well as teleportation of Charlie's qutrit which is encoded in the antisymmetric space of two photons: