Introduction

A Mott insulator is a solid with fractionally filled electronic bands in which charge carriers do not conduct because of their mutual repulsion. The resulting properties1 are believed to be captured by Hubbard models2,3, where only the screened Coulomb interaction, i.e. the on-site Hubbard-U, is retained. This approach has been widely applied to polymers, transition metal oxides, fullerenes and cuprates4,5,6,7,8,9. Moreover, the Hubbard model can effectively describe optically excited Mott insulators where hot quasi-particles are injected across the gap. The quantum dynamics following such “photo-doping” has been extensively studied in the solid state10,11,12,13.

Non-equilibrium Hubbard physics is routinely explored in ‘artificial solids’ realized by ultra-cold atoms trapped in optical lattices14,15,16,17. However, a powerful feature of these systems is the possibility to accurately and dynamically control the strength of interactions through the Feshbach resonances and the bandwidth via the lattice depth18. In contrast, the ability to control the parameters of ‘real’ materials is far more restricted. While the bandwidth can be statically controlled across a limited parameter space, by using pressure19 or chemical substitutions, the Hubbard-U cannot easily be modified since it is dependent on the atomic physics of each site.

A promising pathway to such control are optical pulses at THz and mid-infrared frequencies, which can be tuned to specific vibrational resonances and modulate the lattice along a chosen normal mode coordinate. Since the photon energies are far below those of the correlation gap, this technique has already been used to switch solids between competing electronic phases20,21 and to create new states not found at equilibrium22. Here, we investigate how vibrational modulation influences the electronic interactions in a Mott insulator. Crucially, the leading-order effect of exciting these localised modes is to dynamically modulate the on-site electronic wavefunction, thereby inducing temporal oscillations and modifying the time-averaged Hubbard-U interaction strength.

The response of a strongly correlated electronic system to such vibrational modulation is not well understood, yet the dynamical states created have new properties and exhibit less dissipation than in the case of quasi-particles excitations, opening up the potential for optical devices with superior thermal management.

Results

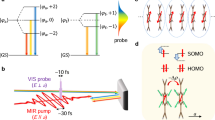
We investigate at room-temperature an organic Mott insulator, bis(ethylendithyo)-tetrathiafulvalene-difluorotetracyano-quinodimethane (ET-F2TCNQ), which is a prototypical system where Hubbard physics accurately describes the electronic transport between individual molecular sites23. The static optical properties of ET-F2TCNQ are shown in figure 1 for light polarized along the chain of ET molecules. A charge-transfer resonance, corresponding to excitations of the type (ET+, ET+) → (ET2+, ET0) is observed at photon energies ~700 meV (5500 cm−1), reflecting the existence of a correlation gap.

Figure 1
figure 1

(a) Crystal structure of the ET-F2TCNQ. The ET molecules form a one-dimensional, half filled Mott-insulating chain along the a axis. (b) Black curves: equilibrium reflectivity (left panel) and optical conductivity (right panel) of ET-F2TCNQ for light polarized along the a-axis (ET chains). The optical conductivity is extracted using a Drude Lorentz fit of the reflectivity. The charge transfer peak in the optical conductivity is fitted to a 10 site numerical solution of the Hubbard model (red) based on the unequal time current-current correlation function (see methods). The best fit is obtained with hopping t ≈ 40 meV, onsite interaction U ≈ 850 meV and nearest-neighbour repulsion V ≈ 120 meV. These values are in agreement with reference 12 and the size of the optical gap in reference 23. A quantitative match with the experimental conductivity is achieved by adding a Lorentzian oscillator centred at 8000 cm−1, which takes into account contributions by higher-lying transitions (blue dashed curve).

Full size image

In the time resolved experiments reported in this work, we measure the broadband optical properties as one localized intramolecular mode is driven with mid-infrared femtosecond pulses. These were generated by difference-frequency mixing of two near-infrared pulses, obtained by parametric down-conversion of a single 800 nm wavelength femtosecond pulse. The excitation pulses were polarized perpendicular to the chains, driving an infrared active molecular vibration close to ~10 μm wavelength (Ω = 1000 cm−1)24. This 10 μm mode was excited with field strengths up to 10 MV/cm, thus strongly deforming the molecular oscillators and local molecular orbitals (see supplementary information).

The tuneable output of the second optical parametric amplifier was used to probe the reflectivity changes along the ET molecule chains in the mid (1800–3000 cm−1) and near infrared (4000–7000 cm−1). The THz response was probed between 25 and 85 cm−1 using single-cycle pulses generated by optical rectification in ZnTe.

When excited by the mid-infrared pump pulses, a shift of the charge transfer band to lower frequency was observed, along with new distinct peaks inside the gap (figure 2a). In this driven state, no reflectivity change was detected for frequencies above the charge transfer resonance and no metallic response was detected in the THz range, where the reflectivity remained low and the phonon resonances unscreened (see figure 2b). The lack of a low frequency response clearly sets this modulated state apart from the photo-induced formation of metallic state by above gap optical excitation, for which a Drude-like metallic response is typically observed25. Secondly, the rapid relaxation back to the ground state makes this experiment different from the case of the vibrationally driven phase transitions, where THz frequency excitation can lead to switching between competing orders26,27. As the excited mode relaxes, the vibrational oscillations are reduced and the effects vanish as seen in figure 2a. By 0.5 ps after the excitation, the peaks inside the gap are strongly reduced and the charge transfer band shifts back to its equilibrium position. Relaxation back to the ground state occurred with a double-exponential decay (τ1 = 230 fs and τ2 = 4.5 ps). The first fast time constant we interpret as the direct relaxation of the system in the vibrational excited state. The second long time constant we assign to a general thermalization of the hot mode with the whole crystal lattice that also involves low frequency phonon modes at THz frequencies resulting in the ps-time constant. The response is also mode selective. When the excitation wavelength was tuned away from the frequency of this vibration, the mid-infrared resonances disappeared.

Figure 2
figure 2

(a) Time and frequency dependent reflectivity after selective modulation of the infrared active molecular mode at 10 μm wavelength. (b) Frequency dependent reflectivity at equilibrium (black) and at the peak of the modulating infrared field (red). Full circles indicate experimental data, whilst the dashed line is a Lorentz fit to the data to extract the optical conductivity. In the low-frequency range (below 100 cm−1), the full lines indicate the equilibrium (black) and transient (red) reflectivity measured with single-cycle THz-pulses. The two peaks are phonon modes of the molecular crystal.

Full size image

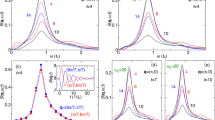
Quantitative analysis of the transient optical properties starts from fitting the broadband reflectivity spectra of figure 2b with a Drude-Lorentz Model and transforming it into optical conductivity28. The conductivity lineouts are shown in figure 4c. The red-shift of the charge transfer band occurs from its equilibrium position at ω/c ≈ 5500 cm−1 toward 5000 cm−1 and a new band is observed approximately at 4200 cm−1. Additionally, a mid-gap resonance and a weaker peak appeared at ~3000 cm−1 and ~2000 cm−1, respectively.

Figure 3
figure 3

(a) Each charge transfer excitation creates an empty site (holon) neighbouring a doubly occupied site (doublon). The holon-doublon pair involves a repulsive energy U and a binding energy of V, totalling U − V. (b) On each site electrons in the valence orbital of the ET molecule are coupled to a harmonic oscillator explicitly modelling the selected vibrational mode. For the 10 μm mode the coupling to the electrons is expected to “stiffen” the oscillator when one electron is removed (holon) and to “slacken” when one electron is added (doublon).

Full size image
Figure 4
figure 4

(a) Schematic representation of the vibrational transitions assuming for simplicity Ωh = Ω. The double-occupied site has a significantly renormalized vibration, which results in new transitions in the optical conductivity. The pn are the occupations of the driven lower vibrational ladder. (b) Theoretical optical conductivity at equilibrium (as in figure 1b) upon coherent excitation of the local vibrational mode. The green and red curves represent two different driving amplitudes. The various peaks are labelled according to the transitions of (a). The dashed curve represents the case in which the asymmetry between holons and doublons are inverted, i.e. in where the holons are stiffened by a factor of 4 and the doublons remain almost unpertubed. (c) Optical conductivity calculated via Drude Lorentz fit to the reflectivity spectra of figure 2b, at two selected pump-probe delays. The background oscillator of figure 1b has been subtracted.

Full size image

To analyse these data, we start from a description of the static optical properties of this compound using the extended Hubbard Hamiltonian,

In this expression and are creation and annihilation operators for an electron at site with spin σ, is its corresponding number operator and . The optical response of the system at high photon energies is probed by the creation of Hubbard excitons29 (figure 3a), composed of a doubly occupied “doublon” site with repulsive energy U, bound to an neighbouring empty “holon” site by a −V attractive energy. The static optical spectrum features a delta peak located at ωCT = U − V − 4t2/V, corresponding to the Hubbard exciton and a broad continuum centered about U, with a bandwidth of 8t, corresponding to unbound holon-doublon excitations. Figure 1b shows that the measured spectrum is well fitted by the extended Hubbard model optical conductivity once a background contribution from a high frequency oscillator (dashed blue curve) is added.

To describe the vibrationally-driven state, we consider the model shown in figure 3b. To each molecular site we explicitly introduce a harmonic oscillator describing the selected molecular mode that gives a locally vibrating Hubbard model30

Here is the sum of local harmonic oscillator Hamiltonians each with angular frequency Ω, displacement and ground state size α0. The term takes into account the coupling between the charge and driven mode and is expected to depend on the electronic configuration as , where f and g are general functions. Typical electron-phonon interactions within the Holstein31 model would only retain a linear coupling to the charge density as . However, a Holstein model is not sufficient to describe the “sloshing” motion of the infrared active distortion (see supplementary information) since by symmetry linear couplings vanish. Instead we find (see Methods) that the vibration has a dipolar coupling to the charge sector which to leading order gives an interaction

where and are the local holon and doublon projectors, with respective positive couplings and .

In addition to coupling to the vibration quadratically, crucially it also depends on the double occupancy as making a form of dynamic Hubbard model27. This type of model, which is natural extension of the Holstein-Hubbard physics, was originally introduced by Hirsch27 to energetically account for reductions in the Hubbard U arising from two electrons occupying the same site. As we shall show the similarity of this effect to the vibrational driving here necessitates the use of a dynamic Hubbard model in order to capture the experimental findings.

Discussion

To analyse the experimental data of figure 2 we computed the real part of the optical conductivity σ(ω) of via the unequal time current-current correlation function32,33 χjj(ω). The narrow hopping bandwidth of ET-F2TCNQ, as well as the strong binding of holon-doublon pairs, justifies σ(ω) being calculated analytically in the atomiclimit where electron hopping is neglected (see Methods). The key effect of vibrational excitation are revealed by considering the infinitely heavy oscillator limit, where its classical displacement varies harmonically in time τ as q = Qcos(Ωτ), with amplitude Q and Ω = 1000 cm−1 the frequency of the driven molecular vibration. Thus, the onsite interaction matrix element U is modulated by (h − d)q2 and results in two crucial features. First, the q2 ∝ Q2[1 + cos(2Ωτ)] dependence predicts a shift of the charge transfer resonance, by an amount that depends on the amplitude of the driven mode Q. The charge transfer resonance is expected to red-shift if the doublon coupling exceeds that of the holon and therefore the time-averaged U is effectively reduced. A blue-shift occurs for the opposite case. Second, the classical frequency modulation generates sidebands at multiples of ±2 Ω on each side of the shifted charge transfer resonance. That a shift in the charge transfer resonance is seen in figure 2a, along with the emergence of a mid-gap peak at 2 Ω below, is strong evidence of the quadratic modulation of the interaction U consistent with the dynamic Hubbard model.

A number of experimental features are not captured by the simple classical modulation picture. In particular a sideband is only seen to the red of the charge transfer resonance and additional sub-structure is present. Instead, to better reproduce these experimental line shapes with a dynamic Hubbard model implies a strong holon-doublon asymmetry along with a quantum treatment of a finite mass oscillator (see Methods). As shown in figure 3b, this strongly coupled limit results in back-action of the electronic configuration on the vibrational mode. Specifically, describes a “stiffening” of the oscillator on the holon site, so Ωh > Ω and a “slackening” on the doublon site, so Ωd < Ω34,35. Such abrupt frequency changes are well known to cause squeezing of the oscillators dynamics36,37.

Figure 4b and 4c show the comparison with the optical conductivity extracted from the reflectivity data and a calculation of σ(ω) with strong coupling aimed to reproduce the overall structure of the experimental conductivity data. We obtain a driving strength Q/α0 ≈ 2, a doublon oscillator that suffers a significant frequency reduction to Ωd ≈ 0.26 Ω and a holon's Ωh ≈ 1.10 Ω that is only marginally increased. Therefore the additional sub-structure seen in figure 4b can be attributed to the “slackening” of the doublon oscillator as schematically shown in figure 4a. Crucially, the reduced spacing between energy levels of the doublon oscillator causes the transition frequencies to move into the gap, an effect that is significant only if the vibrational mode is appreciably populated as found from the model parameters to fit the data. This finding is in agreement with the strong experimental excitation of the molecular oscillator. The remnants of the classical sidebands are now located only at low frequencies and are split into multiples of Ω − Ωd. We note that the 10% modulation of the holon frequency is in agreement with the expectations34,35 for a thermal charge ordered molecular state. However, the substantial reduction, by a factor 4, of the frequency for the doublon site goes far beyond any equilibrium predictions. Nonetheless, the greater effect is consistent with the charge distribution of double occupancies lying predominantly near the oscillating C = C bond38,39.

By way of comparison, we also report the response when tuning the pump wavelength to 6 μm, near a weakly infrared-active symmetric mode along the chains40. This vibrational mode is expected to have a linear coupling. As shown in figure 5, only a reduction in spectral weight at the charge transfer resonance was observed, without any shift or significant response at other wavelengths. As expected, this indicates a dependence of the optical response on the coupling strength, driving and symmetry of the selected vibrational mode.

Figure 5
figure 5

(a) Time and frequency dependent reflectivity after modulation at 6 μm wavelength. (b) Frequency dependent reflectivity at equilibrium (black) and at the peak of the modulating infrared field (red). Full circles indicate experimental data, whilst the dashed line is a Lorentz fit to the data.

Full size image

This experiment demonstrates how for this compound selective vibrational excitation of intramolecular modes can, to first approximation, cause a dynamical modulation of the on-site Hubbard-U interaction. Such control is not easily accomplished by other means and the method is likely to be applicable to a broader class of organic materials. More refined analysis of the observed lineshape carries important information about the microscopic interactions of the material, such as holon-doublon asymmetry. Most importantly, the response to such strongly driven vibrational modes reveals the strength of their coupling to the electronic structure.

More generally, the selective modulation of one degree of freedom, when combined with probing of the electronic spectrum, raises the tantalising prospect of experimentally deconstructing the Hubbard Hamiltonian, by exposing one specific coupling that would otherwise have a vanishingly small contribution to the equilibrium properties. The deconstruction obtained by such quantum modulation spectroscopy should be applicable to more than one class of modes, including charge, magnetic or orbital excitations.

Methods

Coupling of local modes to electrons

In general a spin-independent coupling between a local harmonic oscillator and the electronic configuration of a site can be written in terms of and only, as the number operator is fermionic. We assume that this coupling can be expressed as , where and are two functions of the local mode coordinate that are not known a priori. By expanding the functions f and g into a Taylor series we obtain

with coupling constants Ai, Bi which are constrained by the symmetry of the molecular modes41. An antisymmetric infrared vibration, such as the 10-μm mode in the experiment, is akin to an oscillating dipole. Within the Born-Oppenheimer approximation this perturbation causes admixing of the valence orbital with higher-lying excited states of differing parity and induces an energy shift that is an even function of , meaning e.g. that A1 = 0. This already precludes that such a vibration can be described by a conventional Holstein-Hubbard31 type interaction. In contrast, a symmetric Raman vibration, such as the mode at 6 μm, is instead captured by an oscillating quadrupole, admixing higher-lying states of the same parity and causing a linear energy shift with non-zero A1.

The second term in the expression for , which includes coupling to the double occupancy, is determined by computing the Coulomb repulsion arising from both electrons occupying the admixed vibrational orbital via where is the distance between the electrons. Retaining these terms is crucial to properly describing how vibrations modify the on-site Hubbard U electronic interactions.

For the infrared vibration the differing parity of the states in the admixture causes U(q) to again vary, to lowest order, quadratically with displacement q (implying B1 = 0), while the Raman vibration retains a linear dependence. It is found that B2 < 0 for the infrared mode because the admixed vibrational orbital spatially expands for any non-zero displacement in this simple model. We finally re-arrange terms to isolate the holon and doublon couplings and to give the expression for in the main text.

Optical conductivity of a vibrating Hubbard chain

Since the system does not display any long-range Neel spin-order and does not contain doublons in its thermal state. It is thus well approximated by a half-filled completely spin-mixed state

where is a spin configuration state of the electronic Mott insulator. Given that higher vibrational states of the localized molecular oscillators are essentially unoccupied at room temperature. To model the vibrationally driven state we assume that each oscillator is prepared instantaneously in a coherent state . The phase of the oscillator on each site is expected to be identical across the sample, however it is not controlled shot-to-shot in the experiment. As such a global averaging of the phase of α is made. We further assume that the relative phase of the oscillators where the holon and doublon becomes incoherent upon optical excitation. Since in the atomic limit these are the only relevant oscillators in the problem, this is equivalent to assuming they are both in a phase-averaged coherent state .

To compute the optical conductivity we start from the unequal time current-current correlation function which is defined as where Θ(τ) is the Heaviside function and is the Heisenberg picture current operator. The regular finite frequency optical conductivity then follows as

where χjj(ω) and are the Fourier transforms of χjj(τ) and its complex conjugate, respectively.

In the atomic limit we obtain the current-current correlation function29

as a convolution of the Hubbard shift

and the onsite vibrational doublon and holon correlation functions

where is the squeezing operator with and pn are the diagonal elements of . The matrix elements weighting the δ functions are Franck-Condon factors and are well known analytically42,43. A similar analysis can proceed for the Raman mode.

Atomic limit and hopping

The optical conductivity is calculated here in the so-called zero-bandwidth atomic limit, where the ratio σ1(ω)/t2 can be obtained exactly. This approach is justified by the parameters of ET-F2TCNQ, which indicate that an adjacent holon-doublon pair will be bound. Thus, once optically excited the contributions of the oscillators at the initial holon and doublon locations will be dominant. Moreover, in the dynamic Hubbard model , the quadratic electron-oscillator coupling causes a suppression of t, analogous to polaronic effects28. A further suppression of the coherent hopping processes occurs once the vibrational modes are driven, similar to the reduction with temperature seen for polarons. For the strong coupling infrared case we estimate that the hopping of holons drops to around 0.2 t, while for doublons it is just 0.05 t. Also, because the oscillator coupling here is to a local molecular mode on each site, as opposed to a collective bath of lattice phonons, vibrational excitation disorders hopping through the chain, further inhibiting holon-doublon motion. Thus, the effects of a finite t are to broaden the dominant contribution to the optical conductivity already captured by the on-site vibrational dynamics. To account for these mechanisms, as well as the spectral limitations of the measurement itself, we introduced an artificial broadening of 0.5 t to the results presented.