Abstract
Electric power-systems are one of the most important critical infrastructures. In recent years, they have been exposed to extreme stress due to the increasing demand, the introduction of distributed renewable energy sources and the development of extensive interconnections. We investigate the phenomenon of abrupt breakdown of an electric power-system under two scenarios: load growth (mimicking the ever-increasing customer demand) and power fluctuations (mimicking the effects of renewable sources). Our results on real, realistic and synthetic networks indicate that increasing the system size causes breakdowns to become more abrupt; in fact, mapping the system to a solvable statistical-physics model indicates the occurrence of a first order transition in the large size limit. Such an enhancement for the systemic risk failures (black-outs) with increasing network size is an effect that should be considered in the current projects aiming to integrate national power-grids into “super-grids”.
Similar content being viewed by others
Introduction
Our society depends on critical infrastructures which deploy us essential goods and services1. Most of such infrastructures have a network structure. In the last decade, stemming from the availability of large data and based on the statistical physicist perspective of the graph theory, a new paradigm to describe large networks has blossomed: the field of Complex Networks2,3. The Complex Network approach is a powerful and unifying tool that enables to treat on the same footing widely different networked systems, ranging from biology to sociology to power grids to Internet and the World Wide Web. In fact, such an approach is not tailored to reproduce the detailed behaviour of a system, but to highlight the possible occurrence of collective (systemic). Hence, the statistical tools of Complex Network Analysis may be of great use to understand salient properties of complex human engineered systems that go beyond the single component behaviour.
Among critical infrastructures, the electrical power grid is perhaps the most crucial one as many other facilities like telecommunications, banking systems, oil and gas pumping and even water depend on the electric power system (EPS)4. EPSs have a long history and since their first appearance in 1881 at Godalming in England they have evolved into one of the most well engineered and robust network infrastructures; nowadays, higher standards for the reliability of interconnected EPS are being developed both in Europe and the US by councils and associations of EPS operators5,6. Nevertheless, not only power outages do occur, but also large outages are more likely than what would be naively expected; in fact, the analysis of historical data reveals that their occurrence has fat tails7,8, implying a significant risk of system-wide failures. Given the disruption and economic damages caused by major outages, understanding the nature of such occurrences is a major problem to be addressed.
An important general question is whether EPSs are subject to emergent behaviour or not. In fact, EPSs are aggregations of large number of simple units and can be analysed as a complex network9. It therefore makes sense to ask if EPSs, as a whole, exhibit additional complexity beyond what is dictated by the simple sum of its parts. To this aim, we investigate if an abrupt breakdown transition could emerge in a simple yet realistic complex network model of power grids focused on cascade failures.
In the context of power systems, a cascading outage is a sequence of failures and automatic disconnections consequent to an initiating event; a system-wide outage is also called “black-out”. The rapid succession of automatic reactions in an EPS happens in a time-scale that is typically too short to stop the process by human intervention. Reactions following an initiating event or events include sequential tripping (disconnection) of transmission lines and generators. Initiating events can be due to natural causes (like a line sagging into vegetation, or high wind or lightning shorting a line) but also to human actions (or inaction) or due to imbalances between load and generation.
While no two cascading outages are the same10, we will study a class of possible outages and analyse their characteristics. In particular, we will consider the fragility of EPSs with respect to outages due to cascades of line overloads causing lines to trip. To this end, we will put under stress both model and realistic EPSs to understand the nature of systemic outages. The nature of the stress will be twofold: first, we will consider the case in which an increasing demand on a fixed infrastructure leads to line overloads and subsequent outages. This would correspond to the case of EPS that are operated to the limit of their capacities in order to maximize profits. Second, we will consider the important case of fluctuations in demands and generation; this is a particularly relevant case since the steady penetrations of renewable sources is introducing in the grids new erratic sources whose effects and consequences on existing power grids have not yet been fully understood.
Results
Model
A particular source of stress to EPS comes to the fact that adjustments in power generation are not real-time but follow fixed time schedules; for example, in Europe the production is fixed in advance the day before and periodic adjustments happen every 15 minutes; therefore, the reaction time (apart from automatic controls/tripping) is generally much higher than the time of propagation of electrical perturbation in the system.
The tripping of lines and generators above their operating limits induced by automatic protective equipments is common to all kinds of cascading outages; while this process is intended to protect costly equipments from damage, it can potentially widen cascade failures10.
Most of the cascade model for power grids are purely topological models based on the local redistribution of power loads upon failure11,12,13,14 and disregard the long range nature of electricity. On one hand, a clear signature of the non-locality of power outages can be found in real data: this is, for example, the case of the tripping sequence of the Western Interconnection WSCC system disturbances in July 2–3, 199615, where the occurrence of subsequent failures in far away lines can be observed. On the other hand, it is possible to have simple yet realistic models respecting Kirchoff laws, like the one introduced by Carreras et al16. In this paper, we will consider a very similar model introduced by Pahwa et al17.
In Pahwa's model, the power grid is modelled as a complex network where nodes represent buses and links represent electrical branches; the initial distribution of loads and sources represents the stress imposed to the grid. The initial power flows on lines are calculated using the DC power flow model (see Materials). If the load on a line goes beyond its capacity, the line trips (disconnects) and power flows are recalculated on the new topology (i.e. the grid MINUS the tripped lines). Such procedure is repeated until convergence (fig. 1). We will refer to such a model as the Overload Cascade Model (OCM).
Algorithm for the Overload Cascade Model (OCM).
According to the initial distribution of loads and sources (representing the stress imposed to the power grid), initial power flows are calculated. If the load on a line goes beyond its capacity, the line trips (disconnects) and power flows are recalculated on the new topology (i.e. the grid MINUS the tripped lines). Such procedure is repeated until convergence. Notice that, while in this paper we employ the DC power flow model31 (see Materials), the OCM algorithm is independent from the power-flow model applied to compute line loads.
Our model does not account for the whole complexity of an EPS; in particular, it disregards both transients and the dynamics of phase angles. Nevertheless, it allows to sort out the role of a class of events always present in any black-out, i.e. line overloads. Another important property of the OCM is that, due to the long-range nature of the interaction, it is amenable to analytic approximations that lead to predict the universal behaviour of the system (see Methods).
To analyze cascades, we will use both IEEE model grids18,19 and the Polish Grid19. Notice that IEEE grids are always employed as a realistic test-bed and are often used as sub-units in the design of real power grids18.
Load growth
A very effective way to understand the breakdown of a system is to stress it up to the rupture point. To such a scope, we consider a growth in the power demand while keeping the network fixed. Such mechanism is not so far from reality, since in recent years the economic competition and deregulation has led the power systems to be operating fairly close to their limits: as an example, the number of daily transactions in the US has grown by roughly 400% since 199820. We model such growth of the demand as a simultaneous increase of all the loads by a factor α and record the fraction f of branches that fail at the end of a cascade.
Due to the long-range nature of electric interaction, mean-field arguments (see Methods) predict the occurrence of a first order transition in the system. Fig. 2 shows the results of the increase of load in four IEEE model grids. Indeed, we observe that a steep breakdown of the grids occurs; unfortunately, data sets for only few real (istic) networks are available.
To further investigate the possibility of a first order transition, we generate model networks of increasing sizes using the scheme of Pahwa et al21 (see Materials). We observe that each realization of a network, due to the randomness, shows a sharp jump in the final fraction f of failures at a different value αc of the load increase. Therefore, we calculate f by averaging over different networks at fixed α − αc. The result for synthetic networks (fig. 3) indeed confirms that the transition is first-order.
Effects of load growth in synthetic networks.
Plot of the fraction f of tripped lines versus the relative load increase α mimicking the growth in power demand. Results are averaged over several (100) realizations of the networks for each size. Since each generated network experiences such a jump at a different critical value αc, the resulting fs are averaged as a function of α − αc. Error bars are of the order of the size of the symbols. Our results show that also in synthetic networks f has an abrupt jump consistent with the mean-field predictions for the model (see Methods).
Load fluctuations
Another important source of stress in power grids are flow fluctuations22; as an example, customer behaviour introduces fluctuations that present both cyclic and stochastic components. The introduction of renewable energy sources has introduced further erratic fluctuations whose size can even invert power flow directions. Such a situation can be troublesome in grids that have been engineered for a top-down distribution of the power and where the flow directions are assumed fixed. In particular, fluctuations beyond the operator's predictions can lead to conditions where power flows exceed the line ratings significantly; in general, distributed generation could compromise the stability of the grid23.
We parametrize the size of fluctuation by allowing the initial loads to fluctuate by a fraction σ and calculate the final fraction of cascaded links by averaging over load fluctuations. Fig. 4 shows the results of the increase of the fluctuations' size σ in four IEEE model grids. Compared to the load increase case, we observe that the breakdown of the grids happens in a smoother fashion but becomes steeper with increasing system size, indicating the possibility of a first order transition in the limit of large networks. Moreover, we observe that a finite fraction of the power lines survives past the transition region, i.e. the system fragments in “islands”.
Effects of load fluctuations for IEEE grids.
Plot of the fraction f of tripped lines versus the relative strength of fluctuations σ. Comparing with the case of increasing load of fig. 1, we see that randomness smoothens the transition; yet, the transition becomes steeper with size, indicating the possibility of a firts order transition in the limit of large networks. Results are averaged over 100 realizations of the noise. Error bars are of the order of the size of the symbols.
To better explore such an effect, we again analyse the behaviour of model networks generated according to the scheme of Pahwa et al21 (see Materials) and average the results over both fluctuations and different networks of ths same size. The results for synthetic networks (fig. 5) indicate that in the case of fluctuating sources there are strong finite size effects smoothening the transition; nevertheless, the transition becomes steeper with growing system sizes, indicating the possibility of a first order transition. Nevertheless, also in this case the breakdown due to fluctuations is less severe since a finite fraction of power lines survives and the system is in an “islanded” state.
Effects of fluctuations in synthetic networks.
Plot of the fraction f of tripped lines versus the relative strength of fluctuations σ. Comparing with the case of increasing load in synthetic of fig. 2, we see that randomness smoothens the transition; yet, the transition becomes steeper with size, indicating the possibility of a firts order transition in the limit of large networks. Results are averaged over 10 networks and over 10 realizations of the noise for each network. Error bars are of the order of the size of the symbols.
Polish grid
We now consider a bigger network of 2746 nodes, the Polish grid (available in19). This network is a snapshot of the national high-voltage Polish power grid obtained from the data collected and used by Polish transmission system operators. Such a network is realistic and, thanks to its size, helps us to further confirm the increasing abruptness of the breakdowns with the size. The upper panel of fig. 6 shows that – as expected – by increasing all the loads in such a grid, the breakdown is abrupt as in a first order transition. The situation is more complicated in the case of random loads. The lower panel of fig. 6 shows the un-averaged results for different realization of the noise (fluctuations). For such a big network we find that for a given realization of the noise the system is either in a safe state (the fraction of tripped links is ~0) or in a systemic failure state (the fraction of tripped links is ~1). At difference with the case of uniform load increase, the transition does not happens at a given σ, but can happen in a whole range of values. In particular, for the Polish grid we find that the grid stays essentially intact when the loads are allowed to fluctuate less than ~6% and that the system comes in a black-out state when loads are allowed to fluctuate more than ~12% of their nominal values. For intermediate values, the system can either be in a safe state or in a black-out state depending on the realization of the disorder. Notice that for such a large network the breakdown is systemic (the fraction of failed links f is either ~0 or ~1) and no “islanding” is present even in the fluctuating case.
Cascade results for the 2746 bus Polish grid.
This network is a snapshot of the national high-voltage Polish power grid obtained from the data collected and used by Polish transmission system operators. In the upper panel we show that the fraction f of tripped lines versus the relative load increase α shows and abrupt jump typical of first order transitions; moreover, breakdowns in such a network are systemic, i.e either all the lines have failed (f ~ 1) or the grid is safe (f ~ 0). In the lower panel, by varying σ, we show the effects of the fluctuations in the loads. Data point corresponds to 10 different realizations of the noise. At difference with the case of uniform load increase, the transition does not happens at a given σ, but can happen in a whole range of values. In particular, we find that the grid stays essentially intact (f ~ 0) when the loads fluctuate less than ~6% and that the system suffers a black-out (f ~ 1) when loads fluctuate more than ~12% of their nominal values. For intermediate values (shaded region), the system can either be in a safe state or in a systemic black-out state depending on the realization of the disorder.
Discussion
Our analysis of real, realistic and model systems indicates that black-outs due purely to line overloads are intrinsically a first order phenomenon as predicted by a simple mean-field modelling of the complex network (see Materials). In particular, stressing the system by uniformly increasing the power dispatched in the grid causes a systemic failure of the lines.
On the other hand, when the breakdown is fluctuation-driven, such a transition is smoothed at finite sizes: this means that bigger systems are more fragile, since their breakdown happens in a more abrupt fashion. On the other hand, in the case of fluctuation-driven breakdowns, small system are seen to survive in a fragmented state where separate “islands” survive: such an effect is not predictable by our mean-field approach and is possibly due to the planar nature of real and realistic grids.
Hence, our results indicate that the realization of the foreseen super-grid projects24,25 could introduce an intrinsic source of systemic risk: in fact, since joining together more networks increases the size of the global grid, it could also enhance its fragility.
By considering static power flow models, we contribute only on a single aspect of power grid vulnerability, i.e. the “static security assessment”26. Hence, we disregard other important phenomena like line tripping due to frequency imbalances generated by the mismatch between demand and generation27. Recent studies hint that tuning the parameters of a grid using a complex network approach could stabilize its dynamics mitigating the impact of such transients28; in general, changing the topology of a network could improve its response to attacks and failures29.
In conclusion, while we have not meant to fully address the whole phenomenology of blackouts and outages in power grids, we have isolated one of the key factor that concur to such phenomena, showing by simulations and the means of a simple mean-field model that overload failures are intrinsically a first order phenomenon where increasing the size of the system enhances its vulnerability to systemic cascades.
Methods
Power Flow models
Power flow models aim to obtain complete information on voltage angles and magnitudes at each bus of a power system at given loads and generation. For an AC (alternate current) system, the power balance equations can be written for each bus (nodes of the network); real and reactive power flow on each branch (edges of the network) and the generator reactive power output can be analytically determined, but due to the non-linear character of the system numerical methods are employed to obtain a solution30. A bus of the system is either classified as Load Bus if there are no generators connected or as a Generator Bus if one or more generators are connected. It is assumed that the real power PD and the reactive power QD at each Load Bus are given, while for Generator Buses the real generated power PG and the voltage magnitude |V| are given. A particular Generator Bus, called the Slack Bus, is assumed as a reference and its voltage magnitude |V| and voltage phase Θ are fixed. The branches of the electrical system are described by the bus admittance matrix Y.
DC power flow
A simplification of the AC power flow equations is obtained by linearising the equations by requiring that bus voltages Vi are fixed and that phase differences θij = Θi − Θj along the branches are small. The resulting linear system of equations constitutes the DC power-flow model31

where Pi is the total power (generation minus load) at the i-th bus,  is the Laplacian matrix with K diagonal degree matrix
is the Laplacian matrix with K diagonal degree matrix  ; the sign of Pi determines if a node is a generator, a load or even a transit node (Pi = 0). Notice that we are neglecting phase shifts of the transformers that would add an extra term in eq.(1):
; the sign of Pi determines if a node is a generator, a load or even a transit node (Pi = 0). Notice that we are neglecting phase shifts of the transformers that would add an extra term in eq.(1):  .
.
For the purposes of EPSs operators, the DC approximation matches fairly enough with the full AC solution32; in fact, DC power flow is on average wrong by a few percent33 with respect to the more computationally intensive AC power flow. Another important characteristic is that the probability distribution of the line loads looks statistically equivalent for the AC as well as the DC approximation34. Neglecting line resistances is a justified assumption because they are very small as compared to their inductive reactances31.
Synthetic power grids
The topology of a network determines the arrangement of nodes in the network and how they are connected to each other. A small change in the network topology, such as removal or addition of nodes and/or links, may lead to changes in the network properties. These changes, in turn, may affect the robustness of the network. With the increasing penetration of distributed sources, the network structure would play a very important role in deciding the threshold beyond which any increase in distributed generation could cause a cascade failure in the system.
There is limited real data available for power grids. In order to have more networks and also to study the effect of different topologies on the robustness of the power grid due to increasing amount of distributed generation, it is necessary to have model topologies, i.e a network generation algorithm to generate synthetic power grid networks.
The Erdos-Renyi model35 and the network generation algorithm of Molloy and Reed36 are the simplest network models that include stochasticity as an essential element in the construction of the network. In these two models the connection of the nodes is completely random and lacks knowledge of the principles that guide the creation of links between nodes. Thus, links in these models are created randomly with a given connection probability p. Another model for creation of random graphs is the Generalized Random Graph model37,38,39 which still keeps the assignment of links random but specifies a predefined degree sequence. Thus, the Generalized model can produce graphs with degree distributions which are not necessarily Poisson. The Generalized Random Graph model was first proposed in 1978 in40 and is also known as the Configuration model.
We notice that, although some steps in the directions of generating realistic power grid topologies have been done41,42, there is not yet a consensus on the networks to employ as model EPSs; for example, in their studies of inter-dependent power grids, Brummit et al. use generalized random regular graphs to generate their model networks43.
Network generation
Our model networks are generated using a variation of the Generalized Random Graph Model and imposing certain constraints on the statistics21. Such constraints come in the form of specifying the desired average degree, the desired maximum degree of the network under construction, the fraction of generation nodes, the fraction of load nodes and the generation/load statistics. For each size N, we generated statistically independent configurations with the same number of links. This was maintained by considering a constant average degree for each of the configurations. The average node degree is given by <k> = 2 M/N where M is the number of links and N is the number of nodes. As an example, for a network of size N = 50, if the average node degree, <k> is considered as 2.8, the number of links M is 70. The impedances, the initial loads and the generators are generated by selecting samples from distributions derived from the impedance, load and generation data of the available real power grid networks18.
In addition, since the generated networks should be as close to realistic networks as possible, we also match the maximum node degree of the generated networks with the corresponding test networks. Extra care has been taken to ensure that we obtain a connected network with no self loops. In fig. 7 we show the topologies of some of the synthetic networks.
Synthetic networks of different sizes.
Our model networks are generated using a variation of the Generalized Random Graph Model that imposes constraints on the statistics such that the average degree, the maximum degree of the network under construction, the fraction of generation nodes, the fraction of load nodes and the generation/load statistics are consistent with the ones found in the empirical IEEE test networks.
Simulations
We stress real and synthetic networks according to the two protocols of increasing loads or fluctuations. In the first case, loads are uniformly increased

where  are the initial values of the loads and α parametrises the strength of the stress. In the case of synthetic networks, results are averaged over 100 samples for each system size.
are the initial values of the loads and α parametrises the strength of the stress. In the case of synthetic networks, results are averaged over 100 samples for each system size.
In the second case, fluctuations are mimicked by using a random variable ξi uniformly distributed in [−1, 1]:

i.e. Li(σ) ∈ [(1 − σ)Li, (1 + σ)Li]. Here σ parametrises the strength of the stress. In the case of the IEEE networks and of the Polish grid, averages are obtained over 100 realizations of the noise. In the case of synthetic networks, averages are obtained over 10 realizations of the noise for each of 10 separate network samples.
Mean field analysis
Flows in power grids have complex dynamics even in the DC approximation: if a single line gets overloaded or breaks, its power is immediately distributed, not to a single different branch, but in the whole system, due to the long-range nature of Kirchoff's laws. The redistribution of power after a component failure is dependent on the electrical characteristics (such as impedances) of the lines; if the redistribution of power leads to subsequent overloadings, the consequence could be a cascade of overloading failures. In general, after an initial failure, some of the lines could get overloaded and fail: this represents the first stage of cascade. First stage could possibly lead to further overloading and collapses, constituting the second stage and so on. In this way, the system goes through multiple stages of cascades until it finally stabilizes and there are no more failures.
We indicate the final stable configuration of the OCM by {y}, where

and |yijθij| < Cij, where θij is the phase angle difference among nodes i,j and Cij is the threshold flow (the capacity) beyond which a branch becomes overloaded and fails.
Following Zapperi et al.44, the stable configuration of the OCM can be obtained from a double minimization of an objective function

where cij = Cij/Yij and yij ∈ {0, Yij}. Here H is minimized both with respect to the global variables θij at fixed yij (notice that DC power flow implicitly minimizes the “dissipations”  ) and with respect to the local variables yij at fixed θij (notice that this term corresponds to the breakdown of overloaded links). In such a form, the OCM can be mapped in the model for the breakdown of a disordered media of reference44, indicating that the cascade transition in power grids is a first order transition, i.e. consists of an abrupt failure of the system.
) and with respect to the local variables yij at fixed θij (notice that this term corresponds to the breakdown of overloaded links). In such a form, the OCM can be mapped in the model for the breakdown of a disordered media of reference44, indicating that the cascade transition in power grids is a first order transition, i.e. consists of an abrupt failure of the system.
The first-order nature of such a transition stems from the interplay of the long range nature of Kirchoff's laws and the distribution of failure thresholds45. Long-range interactions allow to apply mean field analysis to the model; in particular, it is possible to assume that when a line is tripped, its load could re-distribute equally among all other lines. Subsequently, the lines above their threshold would trip again, their loads would be re-distributed and so on up to convergence: such a model corresponds to the so called democratic fiber-bundle model (DFBM)46,47. Depending from the distributions of threshold, the DFBM can have at the same time an abrupt breakdown of the system and a power-law distribution of cascade sizes45; such behaviour resembles the hybrid transition for multiplex networks48.
The DFBM model shares the same mean-field spirit of the CASCADE model for black-outs49; notice that while DFBM assumes a starting situation in which loads are the same and thresholds are randomly distributed, CASCADE assumes that loads are randomly distributed and thresholds are the same. While the CASCADE model predicts a self-organised second order critical point, our OCM predicts a first order transition; a recent analysis on black-outs' sizes in several countries indicates that causal factors other than self-organization or a critical state might be significantly ruling the system dynamics8.
Finally, we recall that, by identifying phase differences with voltage drops, the DC power flow equations are equivalent to the equations for DC currents on a resistor network; therefore, our model can also be mapped in the so-called random-fuse model50.
In the following, we analise the case of increasing loads and of random fluctuations in a simple DFBM-like model for the power grid, showing that mean-field predicts a first order transition both in the case of increasing loads and increasing fluctuations.
DFBM with increasing loads
We consider M lines where each link i is characterised by its capacity Ci (maximum amount of flow) and assume that capacities are characterised by a probability distribution ρ(C). When the load of a link surpasses its capacity, the link breaks and its load gets redistributed “democratically” among the remaining surviving links.
We first consider a uniform stress situation, where the system is subject to a load L and all the links are initially subject to the same load l = L/M. Let's consider a cascade of failures in a mean field approach: a fraction of links  immediately fails since their thresholds are less than the load l they sustain. Hence, after the first stage of a cascade, there are M1 = (1 − f1)M surviving links and the new load per link is l1 = L/M1. The cascade's stages follow analogously; we can thus write the mean field equations for the (t + 1)-th stage of the cascade:
immediately fails since their thresholds are less than the load l they sustain. Hence, after the first stage of a cascade, there are M1 = (1 − f1)M surviving links and the new load per link is l1 = L/M1. The cascade's stages follow analogously; we can thus write the mean field equations for the (t + 1)-th stage of the cascade:

where  is the cumulative distribution function associated to p(C). Eq. 6 can be simplified in a single equation for the fraction f of failed links
is the cumulative distribution function associated to p(C). Eq. 6 can be simplified in a single equation for the fraction f of failed links

Hence, the fixpoint f* = F(f*) of eq. 7 represents the fraction of links survived to the failure cascade. The behaviour of f* depends on the functional form of p(C)45 and is known to present a first order transition for a wide family of curves. Thus, it is important to understand the functional form of the distribution for the thresholds C in the case of realistic power networks. In fig. 8 we show the histograms of the normalised line capacities c = C/Cmax where Cmax is the maximum line capacity of the network. For all the networks we find that such histograms can be approximated by p's of the form

where cmin ~ 0.02 for all the networks and the exponent  increases according to the size.
increases according to the size.
To highlight the effects of the shape of p(c), we plot in fig. 9 the results for the MF model (the fixpoint of equation 7) for the extreme cases of a flat distribution ( = 0) and of a sharp decrease in the distribution (
= 0) and of a sharp decrease in the distribution ( = 2). We find in both cases that the transition is first order. Moreover, the height of the jump increases for bigger
= 2). We find in both cases that the transition is first order. Moreover, the height of the jump increases for bigger  , indicating that the size behaviour of cascade in power networks could be mainly due to the change in shape of the capacities' distribution with size.
, indicating that the size behaviour of cascade in power networks could be mainly due to the change in shape of the capacities' distribution with size.
Mean-field results for increasing loads The fraction of failures f grows as a function of the initial load per link until the first order transition.
For our mean-field model no islanding is possible since the fraction of failed nodes after the transition is f = 1 (all the links have failed). Left panel: For an initial distribution p(C) ∝ const, the approach to the first order jump is smoother. Right panel: For an initial distribution p(C) ∝ C−2 (typical of larger networks), the first order jump happens with no apparent precursors.
DFBM with increasing fluctuations in loads
To account for the fluctuations in the initial loads, we can generalise the DFBM model to the case where the initial loads on the links are not uniform. Hence, we consider a model in which M links with capacities Ci extracted with probability p(C) have initial random loads  and where the loads of failed links get redistributed equally among the remaining links. The fraction f of unbroken links can be solved numerically by iterating the algorithm of fig. 10.
and where the loads of failed links get redistributed equally among the remaining links. The fraction f of unbroken links can be solved numerically by iterating the algorithm of fig. 10.
The average initial load is  ; for simplicity, we will consider the case where the initial loads
; for simplicity, we will consider the case where the initial loads  are uniformly distributed among 0 and
are uniformly distributed among 0 and  , i.e. between
, i.e. between  with
with  . By solving numerically such system at finite M for different values of the noise
. By solving numerically such system at finite M for different values of the noise  and several realizations of the initial loads, we find that the transition does not happen anymore at a critical value of
and several realizations of the initial loads, we find that the transition does not happen anymore at a critical value of  but can occurr in a region around the mean-field prediction. As an example, we show in fig. 11 the results for 10 realizations of the initial loads in a system of M = 1000 links.
but can occurr in a region around the mean-field prediction. As an example, we show in fig. 11 the results for 10 realizations of the initial loads in a system of M = 1000 links.
Mean-field results for increasing fluctuations.
When we consider fluctuations  in the initial loads around their average value
in the initial loads around their average value  we observe that the transition is still abrupt but can happen in a region around the mean-field predictions (corresponding to Δ = 0). Full circles: results of simulation for 1000 links systems where, for each value of
we observe that the transition is still abrupt but can happen in a region around the mean-field predictions (corresponding to Δ = 0). Full circles: results of simulation for 1000 links systems where, for each value of  , 10 different realizations of the disorder in the initial loads are considered. Thick line: results for the mean field case where no fluctuations are present and all the initial loads are equal to
, 10 different realizations of the disorder in the initial loads are considered. Thick line: results for the mean field case where no fluctuations are present and all the initial loads are equal to  . The shaded area highlights the region (roughly centred around the mean field transition) where the first order transition can occur.
. The shaded area highlights the region (roughly centred around the mean field transition) where the first order transition can occur.
References
PCCIP. Critical foundations: protecting america's infrastructures (last accessed on 26 jul 2013). (1997). URL http://www.ciao.ncr.gov.
Watts, D. J. & Strogatz, S. H. Collective dynamics of small-world networks. Nature 393, 440–442 (1998).
Barabasi, A. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).
Rinaldi, S. M., Peerenboom, J. P. & Kelly, T. K. Identifying, understanding and analyzing critical infrastructure interdependencies. Ieee Contr Syst Mag 21, 11–25 (2001).
Nerc north america electric reability corporation (last accessed on 25 nov 2013). (2006). URL http://www.nerc.com/.
Entso-e european network of transmission system operators for electricity (last accessed on 25 nov 2013). (2008). URL https://www.entsoe.eu/.
report 1010701 (last accessed 5 Dec 2013). Mitigating cascading outages on power systems: Recent research approaches and emerging methods. Tech. Rep., EPRI (2005). URL http://www.epri.com/search/Pages/results.aspx?k=Mitigating%20Cascading%20Outages%20on%20Power%20Systems:%20Recent%20Research%20Approaches%20and%20Emerging%20Methods.
Rosas-Casals, M. & Solé, R. Analysis of major failures in europe's power grid. International journal of electrical power and energy systems 33, 805–808 (2011).
Pagani, G. A. & Aiello, M. The power grid as a complex network: A survey. Physica A: Statistical Mechanics and its Applications 392, 2688–2700 (2013).
Blackout in the united states and canada, april 2004 (last accessed on 26 jul 2013). (2004). URL https://reports.energy.gov/.
Crucitti, P., Latora, V. & Marchiori, M. Model for cascading failures in complex networks. Phys. Rev. E 69, 045104 (2004).
Solé, R. V., Rosas-Casals, M., Corominas-Murtra, B. & Valverde, S. Robustness of the european power grids under intentional attack. Phys. Rev. E 77, 026102 (2008).
Wang, J.-W. & Rong, L.-L. Cascade-based attack vulnerability on the us power grid. Safety Sci 47, 1332–1336 (2009).
Wang, J.-W. & Rong, L.-L. Robustness of the western united states power grid under edge attack strategies due to cascading failures. Safety Sci 49, 807–812 (2011).
NERC. Review of selected 1996 electric system disturbances in north america (last accessed on 26 jul 2013). (2002). URL www.nerc.com/files/disturb96.pdf.
Carreras, B. A., Lynch, V. E., Dobson, I. & Newman, D. E. Critical points and transitions in an electric power transmission model for cascading failure blackouts. Chaos 12, 985–994 (2002).
Pahwa, S., Hodges, A., Scoglio, C. M. & Wood, S. Topological analysis of the power grid and mitigation strategies against cascading failures. In: Proceedings of the 4th International IEEE Systems Conference, 272–276 (2010).
Christie, R. D. University of washington power systems test case archive (last accessed on 25 nov 2013). (1999). URL http://www.ee.washington.edu/research/pstca/.
Zimmerman, R., Murillo-Sanchez, C. & Thomas, R. Matpower: Steady-state operations, planning and analysis tools for power systems research and education. Ieee T Power Syst 26, 12–19 (2011).
white paper 1009317. actors relating to the series of outages on august 14, 2003. Tech. Rep., EPRI (2003).
Pahwa, S., Hodges, A., Scoglio, C. & Wood, S. Topological analysis of the power grid and mitigation strategies against cascading failures. In: Systems Conference, 2010 4th Annual IEEE, 272–276 (2010).
Heide, D., Schäfer, M. & Greiner, M. Robustness of networks against fluctuation-induced cascading failures. Phys. Rev. E 77, 056103 (2008).
Kroposki, B. et al. Renewable systems interconnection: Executive summary (last accessed 5 dec 2013). Tech. Rep., National Renewable Energy Laboratory, U.S. Department of Energy (2008). URL http://www.nrel.gov/docs/fy08osti/42292.pdf.
European offshore supergrid proposal - vision and executive summary (last accessed on 25 nov 2013). URL {http://www.trec-uk.org.uk/resources/airtricity\textunderscoresupergrid\textunderscoreV1.4.pdf}.
Desertec foundation: Milestones (last accessed on 25 nov 2013). (2012). URL http://www.desertec.org/en/global-mission/milestones/.
Baldick, R. et al. Initial review of methods for cascading failure analysis in electric power transmission systems ieee pes cams task force on understanding, prediction, mitigation and restoration of cascading failures. In: Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the 21st Century, 2008 IEEE Pittsburgh, PA, July, 1–8 (Ieee, 2008).
Padiyar, K. R. Power System Dynamics: Stability & Control (Andhra Pradesh, INDIA, BS Publications/BSP Books, 2002), 2nd edition edn. ISBN: 8178000245.
Motter, A. E., Myers, S. A., Anghel, M. & Nishikawa, T. Spontaneous synchrony in power-grid networks. Nat Phys 9, 191–197 (2013).
Schneider, C. M., Moreira, A. A., Andrade, J. S., Havlin, S. & Herrmann, H. J. Mitigation of malicious attacks on networks. P Natl Acad Sci Usa 108, 3838–3841 (2011).
Grainger, J. & Stevenson, W. Power System Analysis (McGraw-Hill, New York, 1994).
Gungor, B. Power Systems (Oxford University Press, USA, 1995). ISBN-10: 0155707612 ISBN-13: 978-0155707610.
Overbye, T., Cheng, X. & Sun, Y. A comparison of the ac and dc power flow models for lmp calculations. In: System Sciences, 2004. Proceedings of the 37th Annual Hawaii International Conference on, 9 pp. (2004).
Stott, B., Jardim, J. & Alsac, O. Dc power flow revisited. Ieee T Power Syst 24, 1290–1300 (2009).
Scala, A., Pahwa, S. & Scoglio, C. Cascade failures from distributed generation in power grids. International Journal of Critical Infrastructures Accepted, arXiv:1209.3733 (2012).
Erdos, P. & Renyi, A. On the evolution of random graphs. Publication of the Mathematical Institute of the Hungarian Academy of Sciences 5, 17–61 (1960).
Molloy, M. & Reed, B. The size of the giant component of a random graph with a given degree sequence. Comb Probab Comput 7, 295–305 (1998).
Barrat, A., Barthelemy, M. & Vespignani, A. Dynamical Processes on Complex Networks (Cambridge University Press, 2008).
Jackson, M. Social and Economic Networks (Princeton University Press, 2008).
Hofstad, R. Random graphs and complex networks (last accessed 5 dec 2013). (2010). URL http://www.win.tue.nl/rhofstad/NotesRGCN.pdf. Lecture Notes, Department of Mathematics and Computer Science, Eindhoven University of Technology.
Bender, E. & Canfield, E. The asymptotic number of labeled graphs with given degree sequences. J Comb Theory A 24, 296–307 (1978).
Wang, Z., Thomas, R. & Scaglione, A. Generating random topology power grids. In: Hawaii International Conference on System Sciences, Proceedings of the 41st Annual, 183 (2008).
Hines, P., Blumsack, S., Cotilla Sanchez, E. & Barrows, C. The topological and electrical structure of power grids. In: System Sciences (HICSS), 2010 43rd Hawaii International Conference on, 1–10 (2010).
Brummitt, C. D., D'Souza, R. M. & Leicht, E. A. Suppressing cascades of load in interdependent networks. P Natl Acad Sci Usa 109, E680–E689 (2012).
Zapperi, S., Ray, P., Stanley, E. H. & Vespignani, A. First-Order Transition in the Breakdown of Disordered Media. Phys. Rev. Lett. 78, 1408–1411 (1997).
da Silveira, R. Comment on “tricritical behavior in rupture induced by disorder”. Phys. Rev. Lett. 80, 3157–3157 (1998).
Peirce, F. Tensile tests for cotton yarns, part “v”: the weakest link theorems on strength of long and composite specimens. Journal of Textile Institute 17, T355–T368 (1926).
Daniels, H. E. The statistical theory of the strength of bundles of threads. i. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 183, 405–435 (1945).
Baxter, G. J., Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Avalanche collapse of interdependent networks. Phys. Rev. Lett. 109, 248701 (2012).
Dobson, I., Chen, J., Thorp, J., Carreras, B. & Newman, D. Examining criticality of blackouts in power system models with cascading events. In: System Sciences, 2002. HICSS. Proceedings of the 35th Annual Hawaii International Conference on, 10 pp. (2002).
de Arcangelis, L., Redner, S. & Herrmann, H. J. A random fuse model for breaking processes. J. Physique Lett. 46, L-585–L-590 (1985).
Acknowledgements
A.S. acknowledges the support from US grant HDTRA1-11-1-0048, the CNR-PNR National Project “Crisis-Lab” and EU IP project MULTIPLEX nr.317532. S.P. and C.S. aknowledge the support of the US Department of Energy grant EE-0003812: “Resourceful Kansas”. Publication of this article was funded in part by the Kansas State University Open Access Publishing Fund. The contents of the paper do not necessarily reflect the position or the policy of funding parties.
Author information
Authors and Affiliations
Contributions
S.P. was in charge of the simulations and A.S. of the data analysis. A.S., S.P. and C.S. equally contributed to the writing of the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Pahwa, S., Scoglio, C. & Scala, A. Abruptness of Cascade Failures in Power Grids. Sci Rep 4, 3694 (2014). https://doi.org/10.1038/srep03694
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03694
This article is cited by
-
Increasing the resilience of the Texas power grid against extreme storms by hardening critical lines
Nature Energy (2024)
-
Robustness and resilience of complex networks
Nature Reviews Physics (2024)
-
A review of system modeling, assessment and operational optimization for integrated energy systems
Science China Information Sciences (2021)
-
Symmetry breaking-induced state-dependent aging and chimera-like death state
Nonlinear Dynamics (2020)
-
A cross-disorder connectome landscape of brain dysconnectivity
Nature Reviews Neuroscience (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

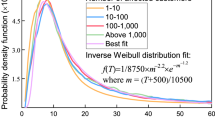









 . Notice that the exponent
. Notice that the exponent  increases with system size.
increases with system size.

