Introduction

In the conventional view of heavy-fermion systems, conduction electrons (c electrons) and localized spins (f electrons) hybridize with each other at low temperatures through the Kondo coupling and form a heavy Fermi liquid. Thereby, a large Fermi surface develops in this approach, which is determined by the total number of c and f electrons. This picture of heavy fermions is supported by experimental findings, since a narrow quasiparticle band is found in the excitation spectrum close to the Fermi energy1,2. From a theoretical point of view, a large Fermi surface follows within a factorization approximation of the Kondo coupling. In the Kondo lattice Hamiltonian

is the kinetic energy of the conduction electrons and is the Kondo exchange (jK > 0). and represent the f and c electron spins. Combining an f creation operator from Si with a c annihilation operator from si and vice versa, expectation values and can be formed, which lead to a mean-field model of hybridized f and c electrons. A more rigorous treatment of the Kondo lattice is based on the so-called large N expansion. Here, N is the f-spin degeneracy, which is artificially driven to infinity3,4. In the limit N → ∞ the key physics is captured as a mean-field theory and properties at finite N are obtained through an expansion in the small parameter 1/N.

Due to the appearance of non-zero amplitudes the mean-field description is related to a broken symmetry and a hybridization gap in the electronic spectrum. These artifacts are circumvented within our approach. A further outstanding drawback of the large N approach is that the cross-over between the heavy Fermi liquid and the local moment physics appears as a sharp phase transition where the 1/N expansion becomes singular5. Moreover, the large N approach can not form two-particle singlets for N > 2, such as Cooper pairs and spin-singlets. Therefore, anti-ferromagnetism and superconductivity are consequently absent from the mean-field theory5. Note that the local f-occupation, , is a constant of motion of the Kondo lattice model, since commutes with the Kondo Hamiltonian. Therefore, the concept of a large Fermi surface in heavy fermions was modified by Oshikawa6 provided that the system can be described as a Fermi liquid. He showed, using rather general arguments that the Luttinger sum rule is fulfilled, when also the completely localized spins contribute to the Fermi sea volume as electrons.

However, it is not obvious that the size of the Fermi surface is large in the Kondo lattice model. In particular, in the one-dimensional case there is evidence based on Density Matrix Renormalization Group (DMRG) and Quantum Monte Carlo (QMC) calculations that the Fermi surface is small7,8,9. On the other hand, for an infinite-dimensional hypercubic lattice a Fermi-liquid state with a large Fermi surface was found10. In this study Dynamical Mean Field Theory (DMFT) and QMC was used avoiding breaking of the gauge symmetry. Evidence of a discontinuity was found in the momentum distribution indicating Fermi liquid behavior.

The DMFT is a widely-used approach to the Kondo lattice which relies on an expansion in powers of 1/d, where d is a variable dimension11,12,13. The idea of the DMFT is to reduce the lattice problem to the physics of a single magnetic ion embedded within a self-consistently determined effective medium. The qualitative physics of the Kondo lattice, including the development of coherence at low temperatures, can well be described by this approach.

Results

Perturbation theory

The aim of the present work is to provide an alternative description of the transformation from localized moment to heavy Fermi liquid behavior as a smooth crossover instead of a sharp phase transition. To avoid technical details, at the beginning let us explain the main idea of our study on the basis of perturbation theory. These considerations will be used afterwards to construct an appropriate many-particle approach to numerically evaluate the electronic spectrum. The one-particle spectral function A(k, ω) of conduction electrons is defined by , where the expectation value and the time dependence are governed by Hamiltonian (1). The presence of the Kondo exchange prevents a straightforward evaluation of A(k, ω). For that reason we transform the Hamiltonian into a diagonal (or at least quasi-diagonal) form by applying a unitary transformation to , . Here the generator X = −X in lowest order perturbation theory with respect to jK is given by

(NL number of lattice sites). The operator quantity is taken over from the decomposition of . Evaluating the transformation to second order in jK, one finds

where is somewhat changed compared to εk. The second term in (3) is the well-known RKKY interaction and is an additional energy constant. Note that in the conduction electrons and the localized spins act as independent subsystems which no longer interact with each other. After an approximate diagonalization of the RKKY interaction, for instance by introducing Schwinger bosons, all expectation values formed with can be determined. However, the evaluation of A(k, ω) also requires the transformation of the operator from which the expectation value is taken. This follows from the general property , for any operator variable , where . Thus, we obtain

where now the expectation value and the time dependence of are governed by . An explicit evaluation of up to second order in X leads for A(k, ω) to the expression

where the coefficients uk and vk′k depend on the initial dispersion of conduction electrons εk and the Kondo coupling jK. Following Doniach's picture of competing energy scales of anti-ferromagnetism and heavy fermion physics in 4f systems14,15, in Eq. (5) we have neglected the excitations of the localized spin system . Note that in the heavy-fermion regime the Kondo scale TK can be considered as large compared to the excitation energies of the f system.

Thus, the one-particle spectrum (5) is built up by a coherent excitation with energy εk and amplitude |uk|2 and by additional excitations at frequencies εk′ with amplitudes |vk′k|2. Usually, such excitations are responsible for a typical broadening of the coherent excitation at εk and determine the lifetime of the quasiparticle in the metallic state. In the present case these are the contributions to |vk′k|2 of order . Beyond this second order perturbation theory we find that the next higher order ∝ of the incoherent part of Eq. (5) leads to the well-known Kondo resonance which has been found by Kondo in case of one magnetic impurity. Namely, taking together in the second term the parts in and Eq. (5) can be rewritten as

with

where |uk|2 was approximated by 1. Note that in third order perturbation theory the expectation value becomes local, which means that all interaction effects between localized spins at different sites do not contribute since they are of higher order. Furthermore note that the sum over q leads to a divergence for εk′ = 0 and the additional excitations in A(k, ω) become dominant. They are located close to the chemical potential ω = 0. Since their energy is momentum-independent, i.e. independent of k, this set of excitations has to be interpreted as the well-known Kondo resonance. The approximate result (7) agrees with the imaginary part of the Green's function for the impurity Kondo model in perturbation theory (compare e.g. with Ref. 16), where . Using moreover the Green's function G(k, ω) in the general form

(real part of the self energy is neglected) one also finds that Γ(ω) has to be interpreted as imaginary part of the one-particle self-energy. Thereby, higher order terms in the denominator of are neglected17.

Note that the perturbation expansion (7) of Γ(ω) in jK breaks down below a characteristic temperature when the second term in the bracket becomes of the order of the first term. This temperature is often used to define the Kondo temperature and is conventionally obtained from an expansion of an effective Kondo coupling18. To see this the sum over q can easily be evaluated

or

where in the last line also the integration over k′ was performed. Here ρ0 is the electronic density of states. In a final step the single-impurity Kondo temperature TK = D exp(−1/jKρ0) is introduced leading to

One should again emphasize that no difference from the single impurity case16,17 has occurred up to now.

The previous considerations are based on perturbation theory leading to a divergence in A(k, ω). This divergence can be removed by including higher order contributions to infinite order in jK. For the single impurity model, higher order perturbation theory leads to equally divergent contributions. This series was summed up by Abrikosov19 in the leading ln(T/TK) approximation to give the following result for the T-matrix, .

Non-perturbative many-particle approach to the 2d-Kondo lattice

The previous perturbation treatment leads to two characteristic problems in the evaluation of the one-particle spectral function A(k, ω). (i) There are contributions to the spectral intensity which diverge and lead to unphysical results. (ii) There is no difference from the single impurity case in lowest order in jK. These problems can only be solved by including higher order contributions to infinite order in jK. In the following, we therefore apply the Projector-based Renormalization Method (PRM)20,21 to evaluate A(k, ω) for the Kondo lattice. The general concept of the PRM (see methods section) is similar to what has been discussed above: To enable the solution of Hamiltonian (1), the Kondo interaction is again integrated out. However, a sequence of unitary transformations is used instead of a single transformation as in perturbation theory. Thereby, the PRM ensures a well-controlled disentanglement of higher order interaction terms leading to an effective Hamiltonian of the same operator structure as in Eq. (2). However, the renormalized parameters , and are determined self-consistently taking into account contributions up to infinite order in the Kondo coupling. Moreover, within our non-perturbative approach expression (4) for A(k, ω) is still valid. The amplitudes uk and vk′,k are also renormalized under the influence of higher order contributions and will be marked by tilde symbols as well. At this point we would like to emphasize the main motivation to develop our own theoretical treatment: Firstly, we note that the perturbative result (6) is also accessible within the PRM by expanding the renormalization equations up to lowest order. Furthermore, our approach has important advances over other theories for the Kondo lattice: The PRM neither suffers from additional constraints, as in the large N approach, nor from an expansion for large dimension d as in the DMFT. Thereby, the local f-electron occupation remains a constant of motion in the calculation.

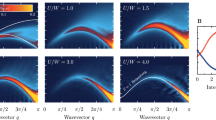
In the actual evaluation of the renormalization equations we restrict ourselves to two dimensions in order to minimize the numerical effort. Also, we consider electron concentrations only away from half-filling which is a special case since there the system becomes insulating. We have solved the renormalization equations self-consistently on a square lattice with NL = 103 lattice points. Fig. 1(a) shows A(k, ω) for T = 0 in a very small k-region around the Fermi momentum kF for electron filling nc = 0.3. Clearly one can see the coherent excitation which crosses the Fermi level at ω = 0. Note that the renormalization of is very weak. This behavior is found to be always true away from half-filling. In contrast, at half-filling nc = 1/2 renormalization contributions to become strong due to nesting effects of the Fermi surface and lead to the opening of a gap at the Fermi energy. This results in an insulating phase22,23 and will be discussed in a forthcoming publication. Moreover, as expected, an additional almost k-independent excitation is found at the Fermi level which corresponds to additional contributions described by the second term in Eq. (5). In contrast to the perturbative treatment the renormalized amplitude is no longer divergent in the PRM. However, it is still dominant for k′ ≈ kF and any value of k. As before, the multitude of these excitations has to be interpreted as Kondo resonance. It results from the second term in A(k, ω) and not from a hybridization effect of f and c electrons. This important feature of the Kondo resonance can also be recognized in Fig. 1(a). In contrast to the coherent excitation, for the Kondo resonance we find a continuous spread of spectral intensity at the Fermi level throughout the whole momentum region. Due to the finite number of lattice points, considered in our calculation, the one-particle kinetic energy is defined only for a finite number of k-points. Therefore the coherent part of A(k, ω), following the dispersion according to the first term of Eq. (5), shows a set of discrete bright spots (19 visible in Fig. 1) which is characteristic for a finite system. In contrast, the second part in Eq. (5) which contributes to the Kondo resonance is made up of an internal sum over all momenta k′ leading to the observed continuous momentum character. Considering finite electron systems, this characteristic feature could possibly be picked up by experiments to find experimental evidence for the different nature of the Kondo resonance. In Fig. 1(b) the spectral function is given in the same wave-vector region as before for the raised temperature of T = 5 · 10−3 t. Now the Kondo resonance has disappeared and only the coherent excitation has survived, which means that T is higher than the Kondo temperature TK. Let us mention that the overall behavior in Fig. 1 looks similar to numerical QMC results24,25 for the periodic Anderson model in one dimension for large values of the Coulomb repulsion U. As is well known, the Anderson model reduces to the Kondo model in the large U limit and low lying energy level εf of the localized f electrons. In particular, in Ref. 24 some f-like bands with low weight were found very close to the chemical potential, two of which seemed almost not to disperse which is quite similar to the behavior of the resonance mode in Fig. 1.

Figure 1
figure 1

(a) One-particle spectral function A(k, ω) for nc = 0.3 and jK/t = 0.3 as a function of ω for fixed values of k = k(ex + ey) in a small wave-vector region around kF. The k-resolved Kondo resonance peak around ω = 0 is clearly seen for all k values. (b) A(k, ω) for the raised temperature kBT = 5 · 10−3 t, which is above the Kondo temperature TK. For fixed k around kF only the coherent excitations survive whereas the Kondo resonances disappear. Note that the discrete bright spots for the coherent excitations are characteristic for finite systems which is not the case for the Kondo resonance.

Full size image

Fig. 2 shows the density of states ρc(ω) = (1/NL)Σk A(k, ω) as a function of ω for three different values of T in a small frequency region around ω = 0. For the two lower T the Kondo peak around ω = 0 appears as a consequence of the Kondo contributions in A(k, ω). The extra background in the spectrum is mainly composed of coherent excitations with respect to different momenta k. Additional incoherent excitations with energies different from zero may contribute to the background as well. We have also checked the sum rule , which at first glance seems to be contradicted by the obvious T-dependence of the different values in Fig. 2. However, the frequency interval outside the restricted ω-region of Fig. 2 also contribute to the sum rule so that the sum rule is almost perfectly fulfilled for the different T curves. Similarly, particle-hole symmetry seems to be present for the curves of Fig. 2. However this is not the case for nc = 0.3 when the full frequency region is considered (not shown).

Figure 2
figure 2

Density of states ρc(ω) for nc = 0.3 and jK/t = 0.3 as a function of ω for three different temperatures, plotted for a small frequency region around ω = 0.

Clearly seen is the Kondo resonance at ω = 0 for the two lower temperature values T = 0 and T = 2 · 10−4 t. For T = 5 · 10−3 t the resonance peak disappears since T is larger than the Kondo temperature TK ≈ 5 · 10−4 t (see text).

Full size image

Discussion

Firstly, let us discuss how the Kondo scale enters the formalism. To address this point, we start from relation , which suggests that the expectation value participates in the formation of the singlet state at low temperatures. In Fig. 3 the expectation value is shown for wave vectors close to the Fermi surface, k′ = k ≈ kF. As expected, turns out to be negative. Moreover, it exhibits a strong increase in magnitude with decreasing temperatures. This behavior is an indication for the formation of the singlet state, to which predominantly wave vectors k′, k close to the Fermi surface participate. In real space this gives rise to correlations 〈Si · sj〉 between local and conduction electron spins which are limited to a range of about 50 lattice sites (see inset). For comparison, Fig. 3 also shows the complete expectation value 〈Si · si〉 as a function of T. Obviously, 〈Si · si〉 is negative as well but almost independent of T. Because of the former relation between 〈Si · si〉 and one concludes that expectation values for wave vectors away from kF are not affected for low temperatures. These wave vectors form the majority in the Brillouin zone, which explains the marginal T-dependence of 〈Si · si〉. The width of in Fig. 3 can be identified with the Kondo scale kBTK and is of order 5 · 10−4 t. The same energy scale is also found in the T-dependence of the electronic part of specific heat CV(T), which can be evaluated in the PRM as well (not shown). For low T a strong increase ~ T is found which is usually associated to a large heavy fermion mass. For T > TK the linear T-slope changes to a much lower value as known from normal metals.

Figure 3
figure 3

Spin coupling for k′ = k ≈ kF as a function of T (black curve).

For T below TK drops to rather small values which indicates the formation of the heavy-fermion state. In contrast, 〈Si · si〉 is almost T independent (red curve). This behavior demonstrates that only wave vectors close to kF contribute to the formation of the heavy-fermion state. The inset shows the correlation function 〈Si · sj〉 as function of (i − j).

Full size image

In conclusion, we have applied the Projector-based Renormalization Method (PRM) to the Kondo lattice model in d = 2 in order to study the electronic one-particle spectrum in the heavy-fermion regime. As main result of our study, we have found that the Kondo resonance is caused by additional low-energetic contributions to the spectral function A(k, ω), which are dispersionless and distributed continuously in momentum space even for a finite electron system. Such a continuous distribution disagrees with a mean-field description of the Kondo resonance and proves that the Kondo resonance is a true many-body effect.

Looking at the electron density nc, one finds that nc is related to the electronic spectral function via . On the right hand side, all excitations from the non-perturbative extension of Eq. (5) contribute. This relation fixes the position of the Fermi energy, when nc is fixed. Using our result for A(k, ω), the Kondo-type excitation turns out to be located slightly below the Fermi energy, i.e. inside the Fermi volume, which is consistent with photoemission experiments. This low-energy quasi-particle is the famous Abrikosov-Suhl resonance indicating heavy fermion behavior which is mainly characterized by a large effective mass of conduction electrons. The resonance emerges from the second term in Eq. (5) in addition to the conventional coherent contribution. Thus, experimentalists might interpret both excitation types, i.e. the coherent excitation and the Kondo resonance, as ingredients of the large Fermi volume within a Fermi liquid picture resulting from a mean-field description.

Unfortunately, the question whether the Kondo lattice in 2d is a Fermi liquid can not be answered by our present treatment. On the one hand, for the electron filling nc = 0.3 considered in this work the results are comparable with the Kondo impurity model, which is known to be a Fermi liquid19,26,27. The Kondo resonance always arises at εk ≈ 0, i.e. at ω ≈ 0 and is wave-vector independent as in the single impurity case. Moreover, we have found that the wave-vector dependence of the spin correlation function 〈Sk–k′ · Sk′–k〉 is rather smooth, i.e. the correlations between local spins at different sites are rather weak. Therefore, we conclude that for parameter values not too close to the quantum phase transition to antiferromagnetism, the impurity physics largely governs the Kondo physics of the lattice model at nc = 0.3. On the other hand, one should emphasize that correlation effects between different lattice sites were found in the spin correlation function 〈Si · sj〉 which is spatially extended in a range of 50 lattice sites (inset of Fig. 3). Thus, long ranging coherence effects between local and conduction electron spins do not disturb the impurity-like behavior of the Kondo lattice. Moreover, for k values on the Fermi surface, k = kF, the numerical evaluation of the quasiparticle weight leads to a very small value. A non-vanishing of the quasiparticle weight (usually called Zk) would be an important evidence that the Kondo lattice in d = 2 has the character of a Fermi liquid.

A possibly simple way to check experimentally the Fermi liquid behavior is to measure the k-dependent occupation number. Note that at finite temperatures the expected jump at kF for T = 0 is smeared out. Therefore, one has to extract the finite temperature effects by use of an adequate Fermi distribution function, which is the usual way to interpret photoemission experiments at low temperatures. A jump at kF would support the Fermi liquid picture.

Methods

Projector-based renormalization method (PRM)

The PRM starts from a decomposition of a many-particle Hamiltonian into an unperturbed part and into a perturbation . The latter part accounts for transitions between the eigenstates of . The basic idea of the PRM is to integrate out the perturbation by a series of unitary transformations. For practical applications the unitary transformations are best done in small energy steps Δλ. Thereby, the evaluation in each step can be restricted to low orders in . This procedure usually limits the validity of the approach to parameter values of which are of the same magnitude as those of . Assuming that all transitions with energies larger than some energy cutoff λ are already integrated out, the transformed Hamiltonian for the Kondo lattice model reads, with

where the operator quantity was introduced before. Due to the elimination of high-energy transitions above λ the coefficients in Eqs. (12),(13) depend on λ. As in the perturbative treatment, an effective exchange interaction between the f spins as well as an energy constant Eλ and a new k-dependence of the Kondo coupling jK are generated by the transformation. The Θ-function in limits the excitations to energies smaller than λ. To find the λ-dependence of the coefficients in we study a subsequent unitary transformation of to a new Hamiltonian

Thereby, all transitions between λ and a somewhat reduced cutoff λ − Δλ will be eliminated. The generator Xλ,Δλ of the unitary transformation

(Θk′k,λ = Θ(λ − |εk′,λ − εk,λ|), is fixed by the requirement that no longer contains excitations with energies larger than λ − Δλ. Since the elimination of transitions is confined to a small energy shell Δλ, the evaluation of from can be restricted to low order contributions in jk′k,λ. Expression (15) is a slight generalization of the generator X, which was used to derive in Eq. (2). By evaluating transformation (14) to order together with (12), (13) we obtain discrete renormalization equations (or flow equations) connecting the coefficients at cutoff λ with those at cutoff λ − Δλ. For instance, the renormalization equation for jk′k,λ reads

where . The complete elimination procedure starts from the original model (1), where the coefficients are fixed to εk,Λ = εk, Jq,Λ = 0, EΛ = 0, jkk′,Λ = jK. Here λ = Λ denotes the largest transition energy of the original Hamiltonian (1). Proceeding in steps Δλ until λ = 0 is reached all transition operators from will be used up. One arrives at the final Hamiltonian , which has exactly the same form as the Hamiltonian of Eq. (3). Thus, from now on quantities with tilde symbols will always denote the fully renormalized quantities at cutoff λ = 0. Note that the explicit evaluation of the unitary transformation leads at first to operator expressions which differ from those of the generic ansatz (12), (13). Therefore, an additional factorization approximation has to be performed in order to trace back these operators to the generic ones. As a result, the renormalization equations also depend on expectation values 〈···〉, which have to be solved self-consistently together with the renormalization equations of . For the evaluation of these expectation values we use the invariance property . To find the desired spectral function A(k, ω) we start from Eq. (4) with . The λ-dependence of is calculated via the following ansatz:

with initial conditions uk,Λ = 1, vk′k,Λ = 0. The operator structure of (17) is suggested from the first order expansion in Xλ,Δλ. The renormalization equations for the λ-dependent coefficients uk,λ and vk′k,λ are obtained by transforming to in analogy to the transformation of . The equation for vk,k′,λ to first order in Xλ,Δλ reads

The renormalization equation for uk,λ can be evaluated in the same way. Alternatively, it can be found from the sum rule , with λ replaced by λ − Δλ

Note that due to (18) the coefficients vq,k,λ−Δλ and vq′,k,λ−Δλ in (19) at cutoff λ − Δλ can be expressed by vk′,k,λ and uk,λ. Thus, equations (18), (19) relate the two quantities uk,λ−Δλ and vk′,k,λ−Δλ at cutoff λ − Δλ with the same quantities at λ. Since the renormalized Hamiltonian has the same decoupled form (3) as in perturbation theory, the renormalization equations (18), (19) together with (17) lead to the final result for the spectral function A(k, ω). Thereby, A(k, ω) takes the same form as (5) but with the fully renormalized parameters of Hamiltonian and of .

As mentioned above, the Kondo resonance results from additional contributions to the spectral function A(k, ω) close to the Fermi surface. Looking at expression (5) for A(k, ω) one notices that only terms from the sum over k′ can contribute to the Kondo resonance which have k′ ≈ kF, so that . At the same time, also the pre-factors become large for the same k′ values. This latter property can be understood by means of renormalization equation (17) for vk′k,λ: Taking k′ ≈ kF and arbitrary values of k ≠ kF, the first term uk,λXk′k(λ, Δλ) on the right hand side of (18) is nonzero but small since Xk′k(λ, Δλ) is small. This follows from the structure of Xk′k(λ, Δλ) in (15). Similarly, in the second term of Eq. (18) those terms from the sum over q contribute most for which q ≈ kF, since then Xk′q(λ, Δλ) is large. Thus, one concludes that terms with wave vectors k′ ≈ kF lead to a finite value of vk′k,λ in the renormalization procedure for λ → 0. This property explains the appearance of the Kondo resonance in A(k, ω), which is almost independent of k [Fig. 1]. On the other hand, from sum rule (19) one can show that for λ → 0 the renormalized amplitude of the coherent excitation in A(k, ω) becomes reduced. For the case k = kF, which was excluded above, the numerical evaluation of the renormalization equations (18), (19) leads to a very small value of the coherent coefficient , which can not be distinguished from zero within the numerical accuracy.