Introduction

Lasers1,2 require an energetically charged (“inverted”) medium, placed inside a cavity. The medium usually consists of excited molecules that interact coherently with a standing wave formed inside the resonator by means of stimulated emission, generating coherent light when the molecules transit to a lower energy state. As a consequence of the discrete nature of the transition process, each host molecule emits only a limited number of wavelengths, restricting the possibility to generate ultrashort laser pulses, which are intrinsically broadband. This restriction is linked to the dual purpose of the lasing material, which acts as an energy storage and also provides a transition with the desired photon energy. Thus ultrashort lasers are limited to a few lasing media and wavelength ranges, mostly in the visible or near-infrared.

In this paper we present Cavity Optical Pulse Extraction (COPE), which readily lends itself as a novel approach for the generation of ultrashort, arbitrary wavelength pulses. The key element is that the storage of energy and the generation of ultrashort pulses are separated, which allows us to use any cw-transition as a master oscillator for an ultrashort pulse, shaped by an ultrashort trigger of a different wavelength. A schematic of the proposed setup is shown in Fig. 1, which underlines its conceptual simplicity. It is based on the established concept of the optical pushbroom3,4,5; where cross-phase modulation induced by a strong trigger pulse “pushes” a slowly propagating burst of light out of a fiber Bragg grating (FBG). In contrast to a conventional push broom scheme, we exploit the intensity enhancement of the resonant cavity mode being extracted by the trigger pulse. We apply the idea to an all-fiber geometry in which the cavity is formed by an optical fiber Bragg grating6,7, employing dynamic wavelength conversion8,9 in the ultrafast regime.

Figure 1
figure 1

Schematic of the COPE setup.

A cw-laser (green wave) excites a cavity mode (green arch) in a FBG cavity (striped cylinder). A counter propagating TP (red pulse) interacts with the energy stored in the cavity and extracts a short pulse, with the same wavelength as the cavity mode (green pulse, superimposed on red pulse). (Inset) Refractive index modulation (blue) and modal profile at the Bragg wavelength (red) of three fiber Bragg gratings (FBGs). (a) Uniform FBG. (b) Uniform FBG cavity with π-phase shift in the center. (c) Sinusoidal FBG cavity as discussed in this paper.

Full size image

In contrast to previous works on pulse generation using dynamically tuned cavities in the adiabatic regime where the transition time is longer than the roundtrip time10,11,12, we exploit an ultrafast non-adiabatic process acting like a shock-front propagating through the cavity13. As a consequence, a short pulse with nanojoule energy or more is extracted from the cavity, even if it has only a moderate Q-factor. Unlike traditional cavity dumping schemes14, COPE does not require a short pulse to be in the cavity but generates it during the extraction process. This results in a light source, which combines the wavelength of an external pump source, with the power enhancement of a grating cavity and the pulse width of an ultrashort oscillator.

We argue that COPE can be considered to be a classical analogue of Hawking radiation15,16,17,18 – generating new wavelengths by means of resonant generation of radiation19,20,21 close to an optical event horizon22,23,24,25. The event horizon is here represented by a refractive index perturbation, induced by cross-phase modulation, moving at the speed of light through the material. Based on this, the COPE pulse is related to Hawking radiation, accumulating close to a moving index perturbation.

The outline of this paper is as follows. We first present a simple analytic model of the COPE process and then in a separate section point out and discuss the analogy to Hawking radiation and event horizons. We then compare our result with fully numerical calculations and discuss issues related to experimental observation. We then briefly discuss our results and conclude.

Results

Analytic description of the COPE process

The propagation of light in a shallow Bragg grating26 is described by the set of coupled mode equations27,28, where for convenience we measure all times in units of c/n,

for A±(z,t), the amplitudes of the mode propagating in forward (+) and backward (−) directions. The frequency detuning is the deviation of the inverse wavelength λ−1 from the Bragg resonance of the grating, which depends on the grating period Λ as λB = 2nΛ. The Bragg wavelength must match a CW laser source but is otherwise arbitrary. The grating itself is characterized by its coupling strength κ(z) = πΔn(z)/λB, proportional to the local, periodic refractive index modulation Δn(z). Depending on the shape of κ(z) an FBG can work as a Bragg reflector or exhibit resonances similar to a Fabry-Perot resonator with distributed feedback. Some examples are given in the inset of Fig. 1. Here we consider a FBG cavity with κ(z) = κ0 sin(π L−1 z) and of length 2L (see Fig. 1(c)), which has a cavity mode at a detuning of δ = 0 with a simple Gaussian form (see Appendix), which allows us to obtain analytic solutions. In a practical implementation of COPE, the specific shape of the cavity mode does not matter and the better-known cavities consisting of a uniform grating with a π-phaseshift6,29 can be used instead (see Appendix). The cavity needs to be sufficiently strong such that

The trigger pulse (TP) interacts with the COPE field via cross phase modulation with the TP's intensity P(z,t); we thus model the TP as an invariant, moving refractive index perturbation. The interaction strength is determined by the cross-phase modulation constant γ = 2πω/(cAeff), where Aeff is the effective area for the nonlinear interaction between the cavity field and the TP30.

Our model aims to provide a fundamental understanding of the COPE process and makes various approximations to achieve this. First we ignore dispersive and/or nonlinear reshaping of the TP during propagation; we do so since the cavity length is usually a few millimeters and therefore much shorter than common dispersion lengths. Furthermore, nonlinear reshaping of the pulse intensity can be slow if the TP experiences normal dispersion, such that soliton self-compression, etc. are absent. The same is true for the COPE pulse. Other approximations, in particular those related to group velocity and dispersion are elaborated in the discussion.

We now show how a substantial fraction of the cavity's energy can be extracted in a coherent ultrashort burst, through cross-phase modulation by the TP. For simplicity we take a TP with a Gaussian shape with an FWHM τ traveling through the grating in the -z direction, such that

It is convenient to decompose the cavity field into a component trapped in the cavity mode , excited by a cw-laser tuned to the cavity resonance and whose shape is given by Eq. (A.17) and the extracted COPE pulse with field B±, which forms in the interaction with the TP. Writing and using Eq. (A.17), we find

The spatial Fourier transform of these equations can be written as

where denotes convolution, ν+ = 1 and ν− = i. We now introduce a second approximation, which allows us to simplify Eq. (5) further. We assume that the pump pulse width τ is much shorter than the localization length of the grating such that

This allows us to ignore the second term on the right hand side of Eq. (5) in favor of the first. With this approximation we replace the parabolic dispersion relation of the grating 31,32, by a light-cone like dispersion relation ω = ± β. This is justified because the spectrum of the extracted pulse is predominantly at frequencies , where the difference between these is small. We discuss this further below.

Next we simplify the last term in Eq. (5), corresponding to the TP. We use the approximations of Eqs. (2) and (6) and the explicit expression for the trapped field Eq. (A.17) derived in the Appendix and Eq. (3) for the definition of the TP, to find

i.e., the interaction between the trapped field and the TP is concentrated at the TP's center.

We now transform the COPE pulse into a frame of reference co-moving with the TP, such that and apply Eq. (6) and Eq. (7) to the evolution equation, resulting in:

The transformation to this frame has a clear physical meaning: it is the frame in which the TP is stationary and the frequency of a wave δ′ is conserved. This not true in the laboratory rest frame, where new frequencies δ are generated because the TP moves. Transformation between the two frames is accommodated by a Doppler frequency shift δ′ = δ + β.

We now derive, starting from Eqs. (8), an analytic expression for the development of the COPE pulse. The TP drives the generation of the COPE pulse via the interaction with the trapped field, which is described by the second term on the right hand side of Eq. (8). The evolution of the COPE fields are, at this level of approximation, decoupled, because most of the spectral components of lie outside the grating-induced band-gap. We can therefore treat the two lines of Eq. (8) separately and immediately find that , because the energy transfer into is not phase matched due to the exponential terms, so the field never accumulates.

We thus only need to solve the second of Eqs (8), which is best carried out after back-transformation into the spatial domain, but still in the co-moving frame of reference:

in which the last term, the product of the pump intensity and the stored field amplitude acts as the source. However if the pump intensity is too high, dephases from the TP and clamps the peak power. After tedious but straightforward calculation we obtain for , at the end of the cavity

The COPE pulse thus has the approximate shape of the squared TP, with a power proportional to the square of that of the TP and to the peak intensity in the grating. The pulse spectrum is dominated by XPM-induced production of side-bands11 proportional to the TP's power. The final factor in Eq. (10), which tends to reduce the peak power, is due to XPM-induced power-clamping due to loss of phase matching between contributions from different parts of the cavity as discussed above. The degree of clamping is determined by the clamping parameter

The peak power of the COPE pulse and the peak position can be readily calculated as

Thus for small clamping parameters (), a single-peaked pulse is generated with a power that is proportional to the TP power. However if the TP is too strong (α > 1) a double peaked pulse is generated. A further increase of the TP's power only leads to an increased separation of the two peaks and does not increase the COPE pulse's peak power further. This is illustrated in Fig. 2.

Figure 2
figure 2

Properties of COPE pulses versus the clamping parameter α (i.e. TP power P0) for (a) a grating with κ0L = 6 (i.e. κ0 = 0.6 mm−1 and L = 10 mm) and a TP with a length of τ = 0.03 (i.e τ = 3 ps).

(red); power enhancement over the linear pump power and (blue) pulse energy versus push parameter α. (b) Near-Gaussian shape of the COPE pulse just before the splitting point. (c) Double-peak shape of the COPE pulse close to the point of maximal pushed pulse energy.

Full size image

Similarly we find for the energy contained in the COPE:

The energy grows with increasing α until a maximum COPE energy is reached at α = 1.84, after which the extracted energy drops. The specific value for this fraction is given by , which means that the fraction of pushed energy is roughly the amount of energy which is stored in the grating on the length scale of the TP. For realistic parameters 10% extraction seems feasible, consistent with our numerical simulations in Section 3. However, energy not extracted from the cavity is not lost, but remains stored and is available to be extracted by subsequent TPs.

As the width of the COPE pulse is close to that of the TP, this is a light source which inherits (i) the pulse width from the TP, (ii) the center wavelength from the cw-pump source and (iii) the power enhancement from the cavity. It is therefore ideally suited to build femto- and picosecond light sources for wavelengths, such as the mid-infrared, for which cw sources are available, but for which ultrashort pulsed sources do not exist.

One further feature is that the clamping of the COPE's peak power is roughly constant for a large range of TP parameters, which makes COPE appear to be an ideal candidate to build ultrafast all-optical power-normals e.g. for the use of pulse counting of discretized signals or telecom pulse bursts, which can be conveniently generated in FBG systems as well33,34. Since the COPE pulse depends only weakly on the TP parameters, COPE can also be used for pulse reshaping.

Analogy with Hawking radiation at an event horizon

The XPM-mediated impact of the TP on the cavity is illustrated in Fig. 3: in the laboratory frame we have the well-known double-parabolic profile of propagating modes, with a grating-induced stopgap for frequencies −κ0 < δ < κ0. The phase-shift imprinted in the grating profile leads to a cavity mode at δ = 0, with a width roughly equal to the inverse localization length , so its (spatial) spectrum has a width κ0. In the absence of the TP the cavity mode cannot couple to any propagating modes, because the frequency δ is conserved and no propagating modes with δ = 0 exist.

Figure 3
figure 3

The COPE scheme's dispersion relation (“light-cone” in relativistic physics) in (a) the laboratory reference frame and in (b) the reference frame co-moving with the TP.

The frequency ω′ is only conserved in the co-moving frame in which the TP is stationary. All co-propagating modes (solid lines) are (nearly) degenerate with the cavity mode (red mark in the center) marked by the green band. These can be excited by momentum transfer due to scattering at the spatial frequencies of the TP (blue, dash-dotted line) marked by the blue band.

Full size image

In contrast, in the presence of the TP the frequency is only conserved in the co-moving frame, here called δ′. Transformation into the co-moving frame tilts the dispersion relation into the shape shown in Fig. 3(b). The photons trapped in the cavity mode are now phase-matched to the backward propagating fiber modes and can be transferred if they gain sufficient transverse momentum β This momentum is supplied by scattering off the TP, which has a spectral width of approximately τ−1 and an amplitude proportional to P0. Thus, a shorter TP allows for larger momentum transfer. In Fig. 3(b) the frequency-degenerate region is marked by the green shade, whereas the range of possible momentum transfer is marked blue. Photons are converted onto those parts of the dispersion relation (red shading) that lie within both regions.

It was shown by Unruh17 and by Philbin et al23 that the TP, moving at the speed of light, is analogous to an event horizon. Based on this starting point, we may attempt to draw a possible analogy between the extracted energy in the COPE scheme and a classical Hawking radiation analogue. The difference is that the radiation is not generated from quantum noise but seeded with bound photons (cavity trapped light), which are swept up by the travelling index perturbation.

We also note the invariance of Eq. (10) with respect to the inversion of time axis and simultaneous conjugation. Therefore photons with positive and negative frequency shift are generated symmetrically with conjugation. As these two branches belong to frequencies above and below the band-gap they are analogous to the correlated pairs of particles of positive and negative energy generated at an event horizon. In an optics picture they are generated by the Doppler-shift of the bound cavity-photons, which are in a grating-mediated state of superposition of forward- and backward moving waves and thus undergo a superposition of Doppler upshift and downshift, generating pairs of photons, with frequencies on either side of the grating's Bragg frequency.

Elaborating on the analogy with relativity, we note that the grating's double-parabolic dispersion relation is equivalent to the dispersion relation of electrons in vacuum32,35. The grating strength κ0 can thus be considered as analogous to the electron rest energy Ee = mec2. Indeed it is predicted that very small, hot, primordial black holes with mean thermal energy kbT of η > 1 times the rest energy of electrons Ee = mec2 and thus a temperature of emit electronic (and positronic) Hawking radiation36,37,38,39. As we have already identified k0 with the quantity analogous to Ee and the mean frequency detuning by the COPE process is we identify η = (τκ0)−1 and therefore get an analogous temperature of the event horizon of

where we took an inverse cavity strength and a pulse length . The expression contains quantities that relate to properties of both the grating and the event horizon: k0 relates to the grating and enters because of its identification with the electron rest energy; , a property of the event horizon, is related to the steepness of the Gaussian pulse, which is in the more general case23 of non-Gaussian pulses. T is the analogous quantity to the inverse black-hole mass in the gravitational case. We stress that Eq. (14) is based on dimensional analysis and should therefore be treated with caution until a full theory is developed.

Though valid only for the electronic part of the Hawking radiation, if confirmed by a detailed analysis and quantum field calculation, this would be to the best of our knowledge the highest analogous temperature ever predicted for classical Hawking radiation in a realistic experiment and should not depend on the existence or seeding of the cavity mode. It shows that our system is not only interesting as a new source for pulsed radiation, but also from a fundamental point of view, allowing the study of analogies to effects which are rare and difficult to observe.

The full system Eq. (1) is only strictly symmetric with respect to the above mentioned transformation if κ(z) was even, as considered in the context of the optical push-broom3,4,5. However we considered a cavity with κ(−z) = −κ(z) which is odd. The solutions of the full system therefore exhibit full spectral symmetry (see Fig. 4(a)) only if the dynamic effect of the cavity on the propagation of the COPE pulse can be neglected, which is true if Eq. (6) holds and the TP is sufficiently weak, as depicted in Fig. 4(b). This asymmetry (or any other asymmetry, induced by background dispersion for example) could also be exploited to validate the thermal character of the Hawking radiation as was shown for shallow water waves15 and optical negative frequency resonant radiation20,21. The fully symmetric generation of negative and positive frequency waves observed here is however consistent with the findings of15. In order to fully validate the analogy, a full calculation based for example on the same methods applied by Hawking and extended to account for the details of our model (i.e. similarly to the analysis in17,23 and summarised by Barcelo et al40) should be considered. However, this is beyond the scope of the present work.

Figure 4
figure 4

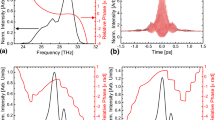
Symmetry of positive energy and negative energy photons generated in the COPE process.

(a) Real and imaginary parts of the spectrum of the COPE pulse for a cavity with κ0 = 0.6 mm−1, a length L = 10 mm and a TP FWHM of 5 ps with clamping parameter α = 0.01. Superimposing the spectrum and its frequency inverted counterpart shows that the positive and negative frequency components are conjugates, as expected for Hawking radiation. (b) The positive and negative energy of (black) a weak cavity with κ0 = 0.3 mm−1 and (red) a strong cavity with κ0 = 0.6 mm−1 and a TP FWHM of 12 ps versus the clamping parameter α and thus the TP power, calculated numerically from Eqs. (1).

Full size image

Simulations and experimental aspects

To validate the analytic results from Section 2 we numerically solved Eq. (1) for realistic cavity parameters and input pulses. For the grating we took κ0 to be smaller than 1 mm−1 and a moderate grating half-length of L = 10 mm, corresponding to κ0L < 10, which is easily achieved for UV written fiber Bragg gratings in GeO2 enriched single mode fibers. The fiber is taken to have an effective refractive index n = 1.5 and a nonlinear constant of γ = 10−3 (mW)−1. The cw-laser which is charging the cavity is taken to have a power of . Parameter scaling for other scenarios can be directly derived from the above equations, or from the parameter scaling section of the methods, where more experimental implementations are discussed.

Results of our simulations are shown in Fig. 5 and Fig. 6. The former shows the evolution of the COPE peak power and energy versus TP power, whereas Fig. 6 shows the temporal shape of the COPE pulses versus TP power. The results in Fig. 5 are given for a weak grating (black lines) with κ0 = 0.3 mm−1 (κ0L = 3) yielding an in-cavity power enhancement factor of 11.4 and a moderate grating (red lines) with κ0 = 0.7 mm−1 (κ0L = 7) with a power enhancement of 1850. Power clamping (α = 1) is predicted at TP powers of 307 kW and 469 kW respectively. The TP length is taken to be τ = 1.2 ps. Agreement with the analytic results from Eqs. (12) and (13), overlaid for comparison, is encouraging; note that the analytic results give the correct trends.

Figure 5
figure 5

(a) Peak power of the COPE pulses for TPs with power P0 and a FWHM of τ = 12 ps for a (black) weak (κ0 = 0.3 mm−1) and a (red) strong (κ0 = 0.7 mm−1) grating of length L = 10 mm and a pump power of , calculated by (solid) the numerical solution of Eq. (1) and as (dashed) predicted by Eq. (12). The output power scales linearly with cw-pump power (b) As (a), but with the COPE's energy shown. The dotted lines denote the clamping power (α = 1).

Full size image
Figure 6
figure 6

Temporal shape and splitting behavior of COPE pulses versus pump power for cavities with length L = 10 mm and a TP FWHM of τ = 12 ps, for a (a) weak (κ0 = 0.3 mm−1) and a (b) strong (κ0 = 0.6 mm−1) grating.

White curves denote the peak position following from Eq. (12). Inequality (6) is not fulfilled for case (b). The output pulse for each trigger pulse power is adjusted to unit peak value, to fill the color scale. The splitting point denotes the clamping power (α = 1).

Full size image

For low TP powers (α < 1) an increase of the COPE peak power and energy is observed, whereas higher TP powers (α > 1) lead to a clamping of the output power and a reduction of the output energy as predicted. For our parameters output pulses of nanojoule energy content with a peak power of a few tens of kilowatts can be expected for a TP power of 100's of kW. As discussed in the parameter scaling section of the methods, a moderate increase in the cavity strength κ0 can lead to the generation of pulses with MW peak power. These parameters are well within the range of modern, commercial short-pulse oscillators or chirped-pulse-amplifier systems. Even the grating with a modest strength of κ0L = 7, leads to more than a 30 dB increase of the COPE pulse over the cw pump. Our scheme can thus be expected to outperform similar schemes such as the push-broom4,5 by orders of magnitude and may be the first in which the non-adiabatic generation of strong ultrashort pulses is achievable.

Given the severe approximation in Section 2 (particularly Eq. (6)) and the fact that the earlier simplifications are not well fulfilled for strong gratings, the qualitative agreement with the numerical results is satisfying. The analytic results slightly overestimate the energy and power of the COPE pulses, which, for all practical purposes, can be countered by slightly increasing the cavity strength κ0L.

The pulse splitting behavior due to the XPM-induced dephasing of the TP and the COPE is shown in Fig. 6 for a weak grating, with κ0 = 0.3 mm−1 and a strong grating with κ0 = 0.6 mm−1. All other parameters are the same as before. White curves are overlaid over the numerical results to show the prediction of the peak position by Eq. (12). While the results agree perfectly for the weak grating, where inequality (6) is satisfied, it still predicts the correct splitting behavior for the strong grating, albeit with an imperfect pulse shape. This is related to the non-vanishing action of the grating on the COPE pulse, which leads to a measurable decrease of the group velocity of the COPE close to the band-edge and a later appearance of the majority of the extracted light.

Fig. 7 gives an insight in the internal dynamics as the TP propagates through the cavity and excites the COPE pulse. Initially the TP modulates the cavity mode very slightly. This modulation grows strongly upon co-propagation with the TP and turns into a distinguishable pulse, which is eventually extracted from the cavity. The dynamics is similar for the two gratings. The only difference is that for the stronger grating a slight splitting of the COPE pulse already occurs for small clamping parameters α < 1, as also seen in Fig. 6(b). Further insight is given by (Media 1) and (Media 2), which show the data of Fig. 7(a) and (b) as movies with much greater temporal resolution and a larger time window.

Figure 7
figure 7

Field evolution inside the cavity – showing the modulus of the backward propagating cavity field (blue, solid), corresponding to the superposition of the trapped field and the COPE pulse and the modulus of the TP (green, dashed).

(a) Weak cavity with τ = 12 ps, κ0 = 0.3 mm−1 and P0 = 275 kW (α = 0.8); (b) Strong cavity with τ = 5 ps, κ0 = 0.6 mm−1 and P0 = 308 kW (α = 0.5). A more detailed view of the evolution is given in (Media 1) and (Media 2) respectively.

Full size image

Discussion

We have investigated the cavity optical pulse extraction (COPE) process, using the cross phase modulation between ultrashort, high-power trigger pulses (TP) and light trapped in a mode of a fiber Bragg grating cavity. We derive an analytic expression for the COPE pulses, which shows that the extracted pulse's power grows exponentially with grating strength and linearly with the pump power. The growth is limited by clamping with respect to the TP power.

The fact that our simple analytic model gives qualitatively similar results to the full numerical solutions of the coupled mode equations (1) shows that, in spite of seemingly drastic approximations, the model captures the essential physics. A key approximation is the replacement of the exact dispersion relation for the COPE pulse, but not for the TP, by a pair of straight lines. This approximation, which is justified for sufficiently short TPs, ignores any grating induced group velocity variations of the COPE pulse. An additional effect, which is ignored in the derivation of the coupled mode equations, is the dispersion of the background medium. The consequence of this effect would be a modification of the dispersion relation at frequencies far from the Bragg resonance, leading to a tilting or curving of the horizontal part of the dispersion relation in Fig. 3b. In turn, this limits the set of wavenumbers generated by the TP; in the lab frame this would correspond to limitations of the spectral content of the COPE pulse. This subtle effect is outside the scope of this paper.

The COPE scheme can produce ultrashort pulses in the range of tens of kilowatts peak power for almost arbitrary carrier wavelengths, limited only by the availability of Bragg grating cavities and cw pump lasers. It is therefore an alternative approach for the generation of ultrashort pulses in wavelength ranges, such as the mid-IR42,43,44,45,46,47,48, which are currently only accessible by nonlinear frequency conversion41 of amplified sources.

An extension towards the MW regime using a Q-switched pump source or intra-cavity dumping seems feasible. While the single shot-efficiency is modest, no energy is lost but remains available in the grating for extraction by subsequent TPs.

We argued that the COPE pulses are generated in a process which is comparable to the generation of electronic Hawking radiation at extremely hot event horizons, allowing for some insight in the dynamics of a process which is otherwise almost impossible to observe. A possible way to stringently make the analogy between the COPE scheme with event horizons and the calculation of the Hawking temperature more rigorous is to exploit (i) the relationship between the CMEs (4) and the Klein-Gordon equation with an external potential; and (ii) the Klein-Gordon equation for a particle in the Schwarzschild metric with spherical symmetry. Written in tortoise coordinates49 it leads to the scalar Regge-Wheeler equation, which would allow a direct mapping of the associated potentials and therefore interpretation of COPE parameters in terms of analogous black-hole quantities.

Methods

Steady state solutions of the cavity

We first look for steady state solutions of Eq. (1), representing a state of a charged cavity before the arrival of the TP. We assume the cavity charge beam to be incident from the left on the grating, which extends from −L to L. The boundaries are thus defined at A+(z = −L) = A−(z = L) = A0 and A−(z = −L) = A+(z = L) = 0 at zero detuning (δ = 0). Eq. (1), then simplifies to

which can be readily solved to give the field envelop inside the cavity

While this solution is valid for any kind of cavity profile κ(z), we shall, for the sake of the availability of sufficiently simple analytic solutions assume a grating of sinusoidal profile such that κ(z) = κ0 sin(πz/L). The approximation of a strong grating Eq. (2) automatically leads to a large field enhancement and further allows us to simplify Eq. (A.16), yielding

Now we can immediately establish the peak power Imax, the stored energy E and enhancement factor of the energy Q as

One sees that the cavity enhances the field exponentially such that even illumination with very moderate powers leads to large amounts of stored energy, limited only by fabrication tolerances.

Parameter scaling

While all results discussed above have been calculated for parameters which can be typically found in UV-written FBG cavities in GeO2 doped telecom type fibers we like to generalize our findings onto another experimental scenario, namely chalcogenide waveguide cavities. Characteristic parameters for these two scenarios a given in Tab. 1. One can see that while UV-written FBG cavities are most suitable for the generation of high energy ps-pulses, chalcogenide cavities are better for the generation of fs pulses.

Table 1 Typical parameters for the COPE scheme in various experimentally motivated scenarios
Full size table