Introduction

A wide range of atomic physics and quantum optics technology provide unprecedented manipulation of a variety of intriguing quantum phenomena. Recently, based on the Berry phase1 and its non-Abelian generalization2, Spielman's group in NIST has successfully generated a synthetic external Abelian or non-Abelian gauge potential coupled to neutral atoms. The realization of non-Abelian gauge potentials in quantum gases opened a new avenue in cold atom physics3,4,5,6,7,8,9,10. It may be used to simulate various kinds of relativistic quantum field theories11,12, topological insulators13,14, graphene15,16 and it may also provide new experimental systems in finding Majorana fermions17,18.

Recently, there have been some experimental19,20 and theoretical activities21,22,23,42,43 in manipulating and controlling of ultracold atoms in a honeycomb optical lattice. Bermudez et al.24 studied Fermi gases trapped in a honeycomb optical lattice in the presence of a synthetic SU(2) gauge potential. They discovered that as one tunes the parameters of the non-Abelian gauge potential, the system undergoes a topological quantum phase transition (TQPT) from the ND = 8 massless Dirac zero modes phase to a ND = 4 phase. However, despite this qualitative picture, there remain many important open problems. In this work, we address these important problems. We first determine the phase boundary in the two parameters of the non-Abelian gauge potential and provide a physical picture to classify the two different topological phases and the TQPT from the magnetic space group (MSG) symmetry21,22,25,42,43. Then we develop a systematic fermionic effective field theory (EFT) to describe such a TQPT and explore its various important experimental consequences. We obtain the critical exponents at zero temperature which are contrasted with a direct numerical calculation on a lattice scale. We derive the scaling functions for the single particle Green function, density of states, dynamic compressibility, uniform compressibility, specific heat and Wilson ratio. A weak short-ranged atom-atom interaction is irrelevant near the TQPT, but the disorders in generating the non-Abelian gauge fields are relevant near the TQPT. We especially distinguish gauge invariant physical quantities from non-gauge invariant ones. When discussing various potential experimental detections of the topological quantum phase transition, we explore the possibilities to choose different gauges to measure both gauge invariant and non-gauge invariant physical quantities. We stress the crucial differences between the TQPT discussed in this work and some previously known TQPTs.

Results

Wilson loops, topological phases and phase boundary

The tight-binding Hamiltonian for Fermi gases trapped in a two-dimensional (2D) honeycomb optical lattice in the presence of a non-Abelian gauge potential [Fig. 1(a)] is:

where t is the hopping amplitude, 〈i, j〉 means the nearest neighbors and create (annihilate) a fermion at site ri of A- and B-sublattice with spin σ. The unitary operator U is related to the non-Abelian gauge potentials A by the Schwinger line integral along the hopping path . For simplicity, we choose a lattice translational invariant gauge [Fig. 1(a)] where the Uij = Ui−j ≡ Uδ, δ = 1, 2, 3. In the momentum space, the Eq. (1) can be written24 as where a, b stands for the two sublattices A, B and also the the two spin indices σ. In the specific gauge in Fig. 1(a), , U2 = 1 and , where the σx and σy are Pauli matrices in the spin-components (The more general case , , can be similarly discussed). The gauge invariant Wilson loop24 around an elementary hexagon is W(α, β) = 2 − 4 sin2 α sin2 β which stands for the non-Abelian flux through the hexagon. However, in contrast to the Abelian gauge case on a lattice21,22,42,43, the W(α, β) is not enough to characterize the gauge invariant properties of the system. One need one of the three Wilson loops W1,2,3 around the 3 orientations of two adjacent hexagons to achieve the goal. In the gauge in Fig. 1(a), W1(α, β) = 2 − 4 sin2 2α sin2 β, W2(α, β) = 2 − sin2 2α sin2 2β and W3(α, β) = 2 − 4 sin2 α sin2 2β. The gauge invariant phase boundary in terms of W and W1 is shown in Fig. 4(a). The W = ±2 and |W| < 2 correspond to Abelian regimes and non-Abelian regimes respectively. Only in the Abelian case W1 = W2 = W3 = 2. The fact that W1 ≠ W2 or W1 ≠ W3 in the non-abelian case shows that the 2π/3 rotation symmetry around a lattice point (or π/3 symmetry around the center of the hexagon) is generally broken, even the translational symmetry is preserved by the non-Abelian gauge field. It is easy to see that the α is gauge equivalent to π ± α and β is gauge equivalent to π ± β, so we can restrict α and β in the region [0, π]. It is important to stress that in principle, the cold atom experiments3,4,5,6,7,8,9,10 can generate various gauges corresponding to the same W and W1,2,3, so the gauge parameters α and β are experimentally adjustable. This fact will be important in discussing experimental detections of the TQPT.

Figure 1
figure 1

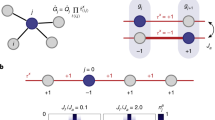
Lattice geometry and phase diagram.

(a) The honeycomb lattice consists of sublattice A (red dots) and sublattice B (blue dots). The up and down arrows represent the spin degrees of freedom. a is the lattice constant. The non-Abelian gauge potentials U1,2,3 with directions are displayed on the three links inside the unit cell. (b) The phase diagram of our system as a function of gauge parameters α and β. The yellow (green) region has ND = 8 (ND = 4) Dirac points shown in the insets. The center C point is the π flux Abelian point. The 4 edges of the square belong to the gauge equivalent trivial Abelian point. We investigate the topological quantum phase transition from C point to D point along the dashed line.

Full size image
Figure 4
figure 4

Finite-T Phase diagram.

(a) The gauge-invariant phase diagram in terms of the Wilson loops W and W1. The yellow (green) regime is ND = 8 (ND = 4). The dashed line corresponds to the one in Fig. 1(b). (b) Finite-T Phase diagram of the topological quantum phase transition as a function of the flux Δ and the temperature T. There is a topological quantum phase transition at T = 0, Δ = 0. The two dashed lines stand for the crossovers at T ~ |Δ|.

Full size image

The spectrum of consists of four bands given by

where the bk = 3 + 2 cos α cos (k1a) + 2 cos β cos [(k1 + k2)a] + 2 cos α cos β cos (k2a) and dk = (1 − cos2 α cos2 β) sin2 (k2a) + sin2 α sin2 (k1a) − 2 sin2 α cos β sin (k1a) sin (k2a) + sin2 β sin2 [(k1 + k2)a] + 2 cos α sin2 β sin [(k1 + k2)a] sin k2a with and . In the following, we focus on the most interesting half-filling case. At the half filling, the spectrum is particle-hole symmetric, the describe the two low (high) energy bands. By solving for k which can be expressed as the roots of a quartic equation, we obtain all the zero modes in analytic forms. For simplicity, we only show the number of the zero modes ND in Fig. 1(b) for general α, β. Especially, the phase boundary in Fig. 1(b) separating ND = 8 from the ND = 4 zero modes is determined by setting the discriminant of the quartic equation to be zero. As the gauge parameters α and β change from 0 to π, the system undergoes a topological quantum phase transition (TQPT) from the ND = 8 massless Dirac zero modes phase in the yellow regime to a ND = 4 phase in the green regime shown in the Fig. 1(b). Along the dashed line in the Fig. 1(b), the TQPT at (α = π/2, βc = π/3) is induced by changes in Fermi-surface topologies shown in the Fig. 2(a)–(d).

Figure 2
figure 2

Topologies of different Fermi surface.

The different Fermi surface topologies of the in the 1st Brillouin zone along the dashed line in the Fig. 1(b). (a) The π flux Abelian point α = π/2, β = π/2 inside the ND = 8 phase, (b) The α = π/2, β = 2π/5 inside the ND = 8 phase, (c) The TQPT at α = π/2, βc = π/3. The two emerging points are located at and its time-reversal partner Q = −P. The four Dirac points are locatedvat , . (d) The α = π/2, β = π/4 inside the ND = 4 phase.

Full size image

Classification of the topological quantum phase transition by the magnetic space group

Time-reversal symmetry indicates that the only two Abelian points are W = ±2 which correspond to no flux and the π flux respectively. For an Abelian flux ϕ = 1/q, the MSG dictates there are at least q minima in the energy bands21,22,42,43. If there exists Dirac points (zero modes), the MSG dictates there are at least q Dirac points in the energy bands. All the low energy modes near the q Dirac points construct a q dimensional representation the of MSG. Due to the time-reversal symmetry, the Dirac points always appear in pairs. When counting the two spin components, each Dirac zero mode was doubly degenerate, so they are counted as ND = 4q Dirac points. W = −2 corresponds to the q = 2 case where there are ND = 8 Dirac zero modes. It is the π flux Abelian point locating at the center in the Fig. 1(b). W = 2 case corresponds to the q = 1 case where there are ND = 4 Dirac zero modes. It is just the graphene case15 running along the 4 edges of the square in the Fig. 1(b). Obviously, the W = ±2 have different Fermi surface topologies, so there must be a TQPT separating the two extremes. It is the non-Abelian gauge field which tunes between the two Abelian points landing in the two different topological phases, induces the changes in Fermi-surface topologies and drives the TQPT. The different phases across the TQPT are characterized by different topologies of Fermi surface26 instead of being classified by different symmetries, so they are beyond Landau's paradigm.

The low energy effective field theory

Based on the physical pictures shown in the Fig. 2, we will derive the effective action near the TQCP at (α = π/2, β = π/3) by the following procedures: (1) Perform an expansion around the critical point β = βc = π/3 and the merging point (or equivalently Q = −P): where the k = P + q, and the Δ ∝ βc − β, . (2) Diagonalize the by the unitary matrix SP: . (3) Perform a counter-clockwise rotation Rπ/6 by π/6 around the point P to align the qx along the colliding direction. (4) Separate Hamiltonian into 2 × 2 blocks in terms of high (low) energy component ϕH (ϕL), then adiabatically eliminate the high-energy bands around −2t and 2t to obtain the effective low-energy two bands Hamiltonian around q = 0 acting on the low energy component ϕL. Finally, we obtain the effective Hamiltonian density in term of effective field ϕL (See Method section)

where , , and the effective field ϕL = [ψ1, ψ2]T is related to the original lattice fields by Eq. (14). When Δ < 0 (Δ > 0), it is in the ND = 8 (ND = 4) phase. We obtain the energy spectrum is quartic (diffusive) in the colliding direction (qx direction), but linear (ballistic) in the perpendicular direction (qy direction) (Similar anisotropy were observed in the collision between two U(1) gauge vortices of two opposite winding numbers μ = ±1 in an expanding universe, see27). Note that the Eq. (3) and Eq. (14) were derived at a fixed gauge, namely along the dashed line in Fig. 1(b), so the position of the merging point P (or Q = −P) will change under a gauge transformation. This fact will play very important roles in the experimental detections of the TQPT and will be discussed in details in the last section.

Applying the same procedures to the four K1,2,3,4 points in the Fig. 2, we obtain the usual Dirac-type Hamiltonian for these points. These four Dirac points stay non-critical through the TQPT, so they just contribute to a smooth background across the TQPT. In the following, we subtract the trivial contributions from the ND = 4 “spectator” fermions from all the physical quantities. All the physical quantities should be multiplied by a factor of 2 to take into account the two merging points P and Q = −P.

The zero temperature critical exponents

Now we investigate if there are any singular behaviors of the ground state energy across the TQPT. So we calculate the gauge invariant ground state energy density and extract its non-analytic part. Its 2nd derivative with respect to Δ around the critical point is (See Method section)

where K(1/2) ≈ 1.85, K(z) is the complete elliptic integral of the first kind and Λ is an ultraviolet energy cutoff in the integral. We define , where ν is the critical exponent characterizing the TQPT. Eq. (4) shows that the exhibits a cusplike behavior with the critical exponent ν+ = −1/2 and ν− = −1. Obviously diverges like Δ−1/2 as the Δ → 0+, but approaches a constant as the Δ → 0−. The TQPT is 3rd order continuous quantum phase transition. In contrast, most conventional continuous quantum phase transitions are 2nd order.

We numerically calculate the ground-state energy density on the lattice scale and illustrate its 1st, 2nd and 3rd derivatives in Fig. 3. Indeed, the exhibits a cusplike behavior near βc = π/3 in Fig. 3(c). Numerically, we obtain the critical exponent ν+ = −1.0 and ν− = −0.5 consistent with our analytical results Eq. (4) (Note that Δ ∝ βc − β). This fact confirms that the effective Hamiltonian Eq. (3) indeed captures the low energy fluctuations across the TQPT.

Figure 3
figure 3

Ground-state energy density.

(a) The ground-state energy density on the lattice scale as a function of β. (b) The first-order derivative of the ground-state energy density on the lattice scale with respect to β. (c) The second-order derivative of the ground-state energy density on the lattice scale with respect to β. It shows a cusp when β = π/3, 2π/3. (d) The third-order derivative of with respect to β. It shows discontinuity when β = π/3, 2π/3, so the system undergoes a third order topological quantum phase transition.

Full size image

Scaling functions at finite temperature

At finite temperature T, the free energy density is

where the is the ground state energy density whose singular behaviors were extracted above. It turns out all the singular behaviors are encoded in . There is no more singularities at any finite temperature, so the TQPT becomes a crossover at any finite T. Following Ref. 28,29, we can sketch the finite temperature phase diagram in the Fig. 4(b). We can write down the scaling forms of the retarded single particle Green function, the dynamical compressibility and the specific heat

where the subscript i = 1 (i = 2) stands for the ND = 4 (ND = 8) phase. Note the anisotropic scalings in qx and qy.

Although the single fermion Green function GR is gauge dependent, the single particle DOS is gauge-invariant. The dynamic compressibility and the specific heat are gauge invariant. The uniform compressibility is given by . We have achieved the analytic expressions for κu(T) and Cv (See method section). Here, we only list their values in the three regimes shown in the Fig. 4(b). For the uniform compressibility, we have

For the specific heat, we have

From Eq. (7) and Eq. (8), we can form the Wilson ratio between the compressibility and the specific heat whose values in the three regimes in the Fig. 4(b) are

Effects of interactions and disorders

Now we consider the effects of a Hubbard-like short-range interactions on the TQPT in Fig. 4(b). It is easy to see is invariant under the local gauge transformation, so the Wilson loops and can still be used to characterize the gauge invariant properties of the interacting system. In this work, we only study the effects of a weak interaction. The low energy form of the was derived in the Method section. Following the standard renormalization group (RG) procedures in30,31 (See Method section), we find the scaling dimension of U is −1/2 < 0, so it is irrelevant near the TQPT at P = −Q. It was known30,31 that the U, with the scaling dimension −1 < 0, is also irrelevant near the Dirac points at K1,2,3,4. So all the leading scaling behaviors will not be changed by the weak short-range interaction. For the quenched disorders Δg in the gauge parameters α, β, following the RG procedures in30,31, we find its scaling dimension is 1/2 > 0, so they are relevant to the TQPT at P = −Q. It was known30,31 that the Δg, with the scaling dimension 0, is marginal near the Dirac points at K1,2,3,4. This put some constraints on the stabilities of the laser beams generating the synthetic gauge field. It would be interesting to look at the interplays between the strong repulsive or negative U and the non-Abelian gauge potentials near the TQPT.

Gauge invariance and gauge choices in experimental detections of the topological quantum phase transition

Due to absence of symmetry breaking across a TQPT, it remains experimentally challenging to detect a TQPT. Very recently, the Esslinger's group in ETH20 has manipulated two time-reversal related Dirac points23 in the band structure of the ultracold Fermi gas of 40K atoms by tuning the hopping anisotropies in a honeycomb optical lattice and identified the two Dirac zero modes via the momentum resolved interband transitions (MRIT). As to be stressed in the disscussion section, in the present synthetic gauge potential problem, the positions of the Dirac points and the two merging points P = −Q shown in Fig. 2 are gauge-dependent, so can be shifted by a gauge transformation. We expect that by tuning the orientations and intensity profiles of the incident laser beams, various gauges corresponding to the same Wilson loops W and W1,2,3 can be experimentally generated. So the MRIT measurement can still be used to detect the positions of the two merging points, the Dirac points and the TQPT at a fixed gauge. Then it can be repeatedly performed at various other experimentally chosen gauges to monitor the changes of these positions as the gauge changes. However, the number of Dirac points ND in the two different topological phases and the density of states ρ(ω) are gauge invariant. In principle, the number of Dirac points ND can be measured by Hall conductivities. The ρ(ω) can be measured by the modified RF-spectroscopy32,33. There are previous experimental measurements on the specific heat of a strongly interacting Fermi gas34. Very recently, Ku et al.35 observed the superfluid phase transition in a strongly interacting 6Li Fermi gas by presenting precise measurements of the compressibility κu and the heat capacity Cv. It was demonstrated that the presence of the optical lattice does not present technical difficulties in the compressibility measurements36,37, therefore these measurements34,35 can be used to detect the uniform compressibility Eq. (7), the specific heat Eq. (8) and the Wilson ratio in Eq. (9). The various kinds of light and atom scattering methods discussed in29,38 is particularly suitable to detect the dynamic compressibility in Eq. (6).

Discussion

In this work, we investigate the topological quantum phase transition (TQPT) of fermions hopping on a honeycomb lattice in the presence of a synthetic non-Abelian gauge potential. The two Abelian phases W = ±2 are connected by the TQPT tuned by the non-abelian gauge parameters. We especially distinguish between gauge invariant and gauge dependent quantities across the TQPT. In fact, the “Abelian path” discussed in24 is just equivalent to the Abelian point W = 2 in Fig. 1(b). The positions of the Dirac cones along the “Abelian path” shown in Fig. 7 in Ref. 24 are gauge dependent quantities and can be shifted by gauge transformations, but the ground state energy density is gauge invariant. In the TQPT in an anisotropic honeycomb lattice studied in20,23, there is no synthetic gauge potential, the collision is between two time-reversal related Dirac points, so the merging points can only be located at half of a reciprocal lattice. Here, the collision shown in Fig. 2 is not between two time-reversal related Dirac points. The locations of the two merging points P = −Q and the four Dirac points K1 = −K3, K2 = −K4 are gauge dependent. But the total number of Dirac points ND, the colliding process and the TQPT shown in Fig. 2 are gauge invariant. In the 3 dimensional TQPT driven by a Zeeman field discussed in26, there is no synthetic gauge potential either, the time-reversal symmetry is broken by the Zeeman field, the collision is between one left handed and one right-handed Weyl fermions at 3d. At the BCS mean field level, the critical effective field theory is a 4-component Dirac fermion at 3d which is different from Eq. (3). So it is a different class of TQPT than that discussed in this paper. As stressed in this work, in principle, the cold atom experiments3,4,5,6,7,8,9,10 can generate various gauges corresponding to the same W and W1,2,3, so both gauge invariant and gauge dependent quantities can be detected in such experiments. In sharp contrast, only gauge-invariant quantities can be detected in condensed matter experiments (For the discussions on gauge invariant Green functions in high temperature superconductors, see39,40,41,44). Indeed, the cold atom experiments of generating synthetic gauge potentials on an optical lattice can lead to new types of TQPT and also offer new opportunities to explore both gauge invariant and non-gauge invariant quantities through the TQPT.

Methods

Derivation of low-energy effective Hamiltonian

We first find the energy bands by diagonalizing Hamiltonian matrix [Eq. (1)] at the critical point βc = π/3 and the merging point . The result is and , where

Now we perform an expansion of the Hamiltonian around the and also around the merging point P by writing k = P + q′ with . Furthermore, we make a π/6 counter-clockwise rotation . Then, we separate the 4 × 4 Hamiltonian into 2 × 2 blocks as and , where the upper left diagonal block HH is the high-energy component, the lower right diagonal block HL is the low-energy component, the off-diagonal blocks HC is the coupling between the two components and ϕ is the corresponding field operator. In the path integral, the quantum partition function is

In order to obtain low-energy EFT, we integrate out high-energy component ϕH

where . Since and HH ∝ t, we can expand (ω − HH)−1 in t−1 and keep only terms up to t−1. After Legendre transform, we obtain the effective two bands Hamiltonian as . After keeping only lowest order derivative terms, we obtain Eq. (3)

where , , . Relation between effective field ϕL = (ϕ1 ϕ2)T and original lattice fields is give by the unitary matrix SP as

where q = Rπ/6(k − P).

Zero temperature critical exponents

The gauge invariant ground state energy density of Eq. (3) can be written as: , where Λx and Λy are ultraviolet moment cutoff for qx and qy respectively. To evaluate such a double integral, we first integrate with respect to qy variable, , where we have defined , and . Due to Λy ≠ 0 feature, singular behaviors are only hidden in f2. In the next step, we need to handle the following integration: .

Let us take derivative before integration, since we have the following simple relation . For the Δ > 0 case, we obtain

for the Δ < 0 case, we obtain

Combining Eq. (15) and Eq. (16), we have following result for ∂2I2/∂Δ2 around the critical point Δ = 0,

Notice that f1 and f2 also have linear contributions, carefully adding these contributions we arrive at the final expression Eq. (4)

where K(z) is the complete elliptic integral of the first kind, K(1/2) ≈ 1.85 and is an ultraviolet energy cutoff.

Finite temperature effect

From Eq. (5) we can directly obtain specific heat as

From Eq. (3), we can get the fermion Green function

where Ps(q) are the project operators for the s = ± band. The dynamical compressibility can be expressed as

Working out the Matsubara frequency summation and trace, we obtain

where nF is Fermi distribution function and Mss′ (p, q) is

Explicit evaluations of Eq. (19) and analytical continuations in Eq. (20), (22) lead to the explicit forms of the scaling functions in the retarded single particle Green function, the dynamical compressibility and the specific heat in Eq. (6). The analytic expressions for the scaling function Ψi in Cv and Ωi in κu(T) are found to be:

where K(z) denote the complete elliptic integrals of the first kind. Their values in the three regimes shown in the Fig. 4(b) are listed in Eq. (7), (8).

Renormalization group analysis of short-range interaction and quenched disorders

We can write Eq. (3) in the action form:

It is easy to see the canonical dimension in (qx, qy, ω) space is [ϕL(qx, qy, ω)] = −7/4. Fourier transforming to (x, y, τ) space leads to [ϕL(x, y, τ)] = 3/4.

Following the same procedures as in the derivation of low-energy effective Hamiltonian, expanding the Hubbard interaction around the merging point and projecting into the low energy component , we obtain the low energy form of the Hubbard interaction: . It is easy to see the canonical dimension of the short range interaction [U] = −1/2 < 0, so it is irrelevant near the TQPT. This is contrasted with the canonical dimension [U]D = −1 < 0 of the short range interaction near the 4 Dirac points K1,2,3,430,31.

Now we consider quenched disorders in the gauge parameter β. As indicated in Eq. (3), at a fixed gauge along the dashed line in Fig. 1(b), the tuning parameter Δ ~ π/3 − β, so the randomness in the gauge parameter β will lead to the randomness in Δ. Similarly, the randomness in the gauge parameters α and γ will also lead to random distributions in Δ in other gauges. We assume all the quenched disorder satisfies a Gaussian distribution with zero mean and variance Δg: where g stands for the gauge parameters α, β, γ. Averaging over the disorders lead to: with . By using the canonical dimension [ϕL(x, y, τ)] = 3/4, one can see the canonical dimension of the short range disorder [Δg] = 1/2 > 0, so it is relevant near the TQPT. This is contacted with the canonical dimension [Δg]D = 0 of the short range disorders near the 4 Dirac points30,31 K1,2,3,4 which is marginal. A RG analysis at one loop is needed to determine its fate30,31.