Introduction

Quantum metrology is one of the most fascinating frontiers of the science of measurement: the counterintuitive laws of quantum mechanics are exploited to maximize the amount of information extracted from an unknown sample, beating the limits imposed by classical physics. The low decoherence of photons, enabling the observation of quantum effects in an easier way, makes optical interferometry a promising candidate for demonstrating quantum enhanced sensitivity. The estimation of an optical phase φ through interferometric experiments is indeed an ubiquitous technique in physics, ranging from the investigation of fragile biological samples, such as tissues1 or blood proteins in aqueous buffer solution2, to gravitational wave measurements3,4. Whereas optical interferometry relying on classical interference is intrinsically a single-particle process, quantum advantages arise when quantum-correlated states of more than one particle are employed5, such as Greenberger-Horne-Zeilinger (GHZ)6 and N00N7 states. N00N states, in particular, allow to saturate the Heisenberg limit of sensitivity: the ultimate limit to the precision of a measurement imposed by the laws of physics.

Generally, the quantum advantage over classical approaches increases with the number of particles involved in the correlated probe state5. Two-photon N00N states can be produced deterministically simply by quantum interference of two identical photons on a balanced two-mode beam-splitter. However, two-mode N00N states with more than two particles are difficult to produce. Increasing the number of modes to more than two represents an interesting possibility to extend the concept of multiparticle interferometry, as pointed out by Greenberger et al.8. This requires multi-port devices, instead of simple two-mode beam-splitters, to build multi-arm interferometers. Multi-port beam splitters can be potentially realized by properly combining several balanced two-port beam-splitters and phase shifters9,10: such implementation has anyway tight requirements on interferometric stability, making its effective realization challenging with bulk optics. In fact, the few experimental realizations of such devices are reported on fiber-based11 or integrated-optics12 multi-mode devices; in both cases the characterization was performed with only two-photon states. Multi-photon interferometry is, indeed, still a widely unexplored field.

Times are mature to demonstrate multi-photon and multi-port devices. In fact, on the one hand in the last few years the efficiency of quantum multi-photon sources have dramatically improved leading to several experiments with up to 8 photons13. On the other hand, the advent of integrated quantum photonics have opened exciting perspectives for the realization of scalable, miniaturized and intrinsically stable optical setups14. In particular, the ultrafast laser-writing technique15,16,17,18 has proved to be a powerful tool for demonstrating new quantum integrated-optics devices, able to perform quantum logic operations19 as well as two-photon quantum walks20,21. This technique exploits nonlinear absorption of focused femtosecond laser pulses to induce permanent and localized increase of the refractive index in transparent materials. Waveguides are directly fabricated in the material bulk by translating the sample at constant velocity along the desired path with unique three-dimensional (3D) capabilities.

In the field of quantum metrology, recent results have demonstrated the possibility of using two-mode path-entangled states in integrated structures for phase estimation below the Standard Quantum Limit (SQL)2,22,23,24. Combination of all the above elements would enable stepping into multi-photon/multi-port quantum metrology. However, the potentials of this approach have not yet been investigated theoretically.

In this work we introduce the concept of 3D multi-photon interferometry. First, we propose novel geometries for integrated multi-arm interferometers based on three-port (tritter) and four-port (quarter) devices. Second, we theoretically study possible measurement protocols, based on the injection of multi-photon Fock states in this kind of multi-port devices, demonstrating relevant metrological advantages in phase-estimation tasks. Our results are not merely speculative since both the realization of such integrated multi-port devices25 and the generation of multi-photon quantum states26 appear to be within reach of present state-of-the-art technology.

Results

Multi-arm interferometric schemes

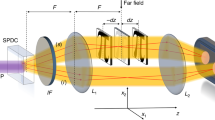
A multi-arm interferometer can be realized by cascading two multi-port beam splitters. In particular, a three-arm interferometer is built by the combination of two tritters and a four arm interferometer by the combination of two quarters. In our approach the integrated-optics multi-port device is devised as a 3D multi-waveguide directional coupler [Fig. 1 (a)-(b)], a structure in which the waveguides are brought close together for a certain interaction length and coupled by evanescent field. The feasibility of such structures, in the case of three-ports (tritter), has already been demonstrated by femtosecond laser writing25,27, albeit characterization has only been performed in a classical framework. Note that in these compact multi-waveguide structures the interaction between the different arms happens simultaneously, without the decomposition into cascaded two-mode beam splitters. This is made possible by the 3D capabilities of femtosecond laser micromachining, thus relaxing the strict requirements on path-length control of alternative approaches.

Figure 1
figure 1

(a) 3D structure of tritter.(b) 3-dimensional structure of quarter. (c) Geometry showing the direct coupling between the three modes of the tritter. (d) Geometry showing the direct coupling between the four modes of the quarter. (e) Indirect coupling between the four modes of the quarter by means of one ancillary mode. (f) 3-mode interferometer built by using two cascaded tritters. (g) 4-mode interferometer built by cascading two quarter devices. (f)–(g) φ: phase to be measured. ψ: additional phase for adaptive phase estimation.

Full size image

The symmetric configuration of a tritter can be easily obtained by adopting a triangular geometry, as shown in Fig. 1 (c). In this configuration it is possible to obtain equal coupling coefficients, so that a single photon entering in one input port has the same probability of exiting from one of the three output ports. The symmetric configuration of a quarter can be achieved by adopting two possible solutions. In the first one, the four modes are directly coupled and the symmetric condition can be obtained by appropriately tuning the interaction length [Fig. 1 (d)]. Alternatively, an indirect geometry may be exploited by coupling waveguides 1-4 through an ancillary mode, as shown in Fig. 1 (e) and without any direct coupling between them.

Output states

We start by considering the action of a single tritter and of a single quarter. The action of these devices on an input state |ψ〉 is expressed by a unitary matrix , which maps the input field operators to the output field operators according to , with k = III, IV9,10,28 (see Supplementary Material). Let’s consider the Fock state |1, 1, 1〉, where is the input state in the tritter. By applying we obtain the output state:

Here , and |{i, j, l}〉 is the symmetric superposition of three-photon states where (i, j, l) photons exit in the three output ports. A similar result is obtained for a quarter fed with a state:

where c1,1,1,1 = 1/2, , . In both cases, we observe that some terms of the output states are suppressed due to quantum interference. They correspond in particular to the contributions {2, 1, 0} in the tritter case, {3, 1, 0, 0} and {2, 1, 0, 0} in the quarter one. This feature is a N-mode analogue of the Hong-Ou-Mandel bosonic coalescence effect28,29,30. The two devices can be exploited to generate maximally-entangled N00N states in a post-selected configuration31.

N-modes interferometry

The 3D, N-port structure of tritter and of quarter devices can be exploited to implement an integrated N-modes interferometer. This can be realized by a chain of two subsequent multiport beam-splitter, leading to a generalized Mach-Zehnder structure [see Fig. 1 (f)-(g)]. The phase shifting could be introduced for instance by adopting a microfluidic channel as reported in Ref. 2,32. Let us now consider the 3-modes system obtained with two tritter devices and the action of a relative phase shift φ in the optical mode k3 inside the interferometer, which is described by the operator , being n3 the photon number operator for mode k3. The output probability distributions Pm,n,q(φ) corresponding to the detection of (m, n, q) photons in the three output ports, are obtained by the overall evolution of the interferometer acting on the input state. Let us consider again an input Fock state |1, 1, 1〉; the obtained fringe patterns , symmetric for an index exchange (m, n, q), are reported in Figs. 2 (a)-(c). We observe the presence of interferometric patterns presenting the sum of different harmonics up to cos(3φ). Furthermore we note that the term presents a sub-Rayleigh λ/3 behavior with a unitary visibility. These results suggest that the output state of the interferometer, for a |1, 1, 1〉 input state, presents nonclassical features. Similar results can be obtained when a 4-modes interferometer is fed with a |1, 1, 1, 1〉 input state [Fig. 1 (g)] (see Supplementary Material).

Figure 2
figure 2

(a)–(c) Output fringe patterns of the 3-modes interferometer fed with a input state.(d) Diagram of the N-fold visibilities of the output fringe patterns for a N = 3 interferometer with a input state, compared with the classical bound . (e) Corresponding diagram for the 4-modes case.

Full size image

Nonclassicality criterion for sub-Rayleigh fringe patterns

In order to formally address the nonclassicality of this setup we have extended the criterion proposed by Afek et al. in Ref. [33] from a 2-modes to a 3-modes interferometer. This criterion sets an upper bound for classical states on the N-fold visibilites of the Fourier expansion of the fringe pattern distributions , where N = m+n+q. The visibilities are defined as the ratio between the Fourier coefficient Am,n,q of the term oscillating as Nφ and the constant coefficient A0, i.e. Vm,n,q = |Am,n,q/A0|. The classical bound for Vm,n,q is obtained by calculating the probability distribution of having (m, n, q) photons in the output modes (1, 2, 3) respectively, by feeding the interferometer with a classical coherent state: |α1, α2, α3〉, where . Then, the N-fold visibility Vm,n,q is maximized with respect to |αi| and θi, leading to max . In general, it can be shown that for any classical state , since any classical state can be expanded in the coherent states basis according to ρC = with a well behaved P(α). The corresponding N-fold visibilities for the input Fock state |1, 1, 1〉 are obtained from the probability distributions shown in Figs. 2 (a)-(c), leading to higher visibilities than the classical limits, except for the case [Fig. 2 (d)]. The same criterion can be extended to a N-modes interferometer. We then repeated the same analysis for the N = 4 case when the interferometer is built by two subsequent quarter devices [Fig. 1 (g)], showing the presence of nonclassical behaviors in the fringe patterns [see Fig. 2 (e)].

Phase estimation

The present interferometric configuration can be adopted to perform a phase estimation protocol. In this context, the aim is to measure an unknown phase shift φ introduced in an interferometer with the best possible precision by probing the system with a N-photon state and by measuring the resulting output state. The classical limit is provided by the SQL, which sets a lower bound to the minimum uncertainty which can be obtained on φ by exploiting classical N-photon states on two modes and M repeated measurements34. Recently, it has been shown that the adoption of quantum states can lead to a better scaling with N, setting the ultimate precision to , corresponding to the Heisenberg limit5,35,36. Hereafter, we show that the present integrated technology can lead to a sub-SQL performance in the estimation of an optical phase, exploiting multi-mode interferometry.

Quantum fisher information

In order to characterize the present 3-modes interferometer fed with a |1, 1, 1〉 input state and analogously the 4-modes case, we need to determine the quantum Fisher information (QFI) of the output state37,38. This quantity sets the maximum amount of information which can be extracted on the phase φ from a state according to the quantum Cramér-Rao (QCR) bound: δφ ≥ (MHφ)−1/2 37. The classical limit is provided by the quantum Fisher information when a coherent state |α1, α2, α3〉 is injected into the interferometer. Note that the comparison between the performances achievable with an input coherent state and an input |1, 1, 1〉 Fock state must be performed for the same number of photons impinging onto the phase shifter. Furthermore, for a coherent state input two different cases can be identified. (i) If an external reference beam, providing an absolute reference frame for the optical phase, is available at the measurement stage, the QFI is calculated for a pure |α1, α2, α3〉 input state: . (ii) If no reference frame is available at the measurement stage (such as for photoncounting detection), one needs to average the input state on a random phase shift θ common to all input modes leading to . In absence of an external reference beam, an input state has to be replaced with the phase-averaged state , where is the phase shift operator for mode ki. The two conditions (i) and (ii) are equivalent for the |1, 1, 1〉 probe, since this state has a fixed number of photons39. We then evaluated the three quantities , , and obtained that the adoption of a |1, 1, 1〉 probe state leads to quantum improved performances. The same result is found for the 4-modes case, as shown in Fig. 3 (a). We note that, while is fixed, the QFI achievable with a Fock state input increases with the number of modes, leading progressively to a greater advantage in phase estimation protocols. Furthermore, no post-selection is needed to generate the required probe state40.

Figure 3
figure 3

(a) Comparison of the QFIs for the N = 2, N = 3, N = 4 interferometers fed with a Fock state a coherent state with an external phase reference beam and a coherent state without an external phase reference beam .(b)–(c) QFI and FI for (b) a 3-modes interferometer with a input state and (c) for a 4-modes interferometer with an input state. The optimal working points are obtained when .

Full size image

Achieving the optimal bound

We now show that the QCR bound provided by can be achieved by adopting a feasible and practical choice of the measurement setup, consisting in a photon-counting apparatus recording the number of output photons on each mode. The detection apparatus can be implemented by splitting each output mode in three parts by means of a chain of beam-splitters and by placing a single-photon detector on each part. The occurrence of 1, 2 or 3 simultaneous clicks of the detectors on the same mode corresponds to the detection of 1, 2, 3 photons. For a fixed choice of the measurement setup, the amount of information which can be extracted on φ is provided by the Cramér-Rao (CR) bound δφ ≥ (MIφ)−1/2 37, where Iφ is the Fisher information of the output probability distribution of the measurement outcomes. The results for with the |1, 1, 1〉 input state and photon-counting measurements are reported in Fig. 3 (b). By comparing the trend of with the corresponding QFI , we observe that the ultimate precision given by the QCR bound can be achieved with this choice of the measurement apparatus for φ = 0, 2π/3, 4π/3. An analogous result is found for the N = 4 case, where the optimal working points are now φ = 0, π [Fig. 3 (c)].

Adaptive protocol

The obtained φ-dependence of the Fisher information Iφ suggests that an adaptive protocol41 is necessary to obtain optimal performances in the full phase range, that is, to saturate the QCR bound for all values of φ. To this purpose, we consider the adoption of a three-step adaptive strategy where the first two steps of the protocol are performed to obtain a rough estimate φr of the phase φ (more details on the protocol can be found in the Supplementary information). The amount of measurements performed in these steps is a small fraction of the overall resources M, namely . In the first step, a rough estimate of the phase is obtained up to a two-fold degeneracy due to the symmetry of the interferometric fringes (φ,4π/3 − φ). The second step is exploited to remove this degeneracy for the estimate φest. Finally, the third step consisting of M3 = M − M1 − M2 measurements is performed by sending the |1, 1, 1〉 input state and the system is tuned to operate in the optimal regime by means of an additional phase shift ψ. At each step of the protocol, the measurement outcomes are analyzed by a Bayesian approach and assuming no a-priori knowledge on φ42. The results of the numerical simulation for M = 105 are reported in Fig. 4, together with the results for a numerical simulation of a one step non-adaptive strategy. We observe that in the latter case, the uncertainty δφ associated to the estimation process resembles closely the CR bound provided by the Fisher information . A better result is obtained with the adaptive strategy, showing that the quantum Fisher information is achieved, leading to sub-SQL performances in the full phase interval. The choice of the Bayesian approach leads to an unbiased estimation process, i.e., the estimated phase φest converges to the true value φ (see inset of Fig. 4) and the error on the estimation process can be directly retrieved from the output distribution for φ43.

Figure 4
figure 4

Results for the phase estimation error δφ of a numerical simulation with M = 105 repeated measurements with the three modes interferometer of Fig.

1 (f). Blue circular points: δφ for the adaptive protocol as a function of φ. Blue solid line: QCR bound given by . Red cross points: δφ for the non-adaptive protocol. Red dashed line: Fisher information , providing the bound for the non-adaptive strategy. Shaded region corresponds to sub-SQL performances achievable with quantum resources. Inset: plot of the difference between the true value φ and the estimated value φest obtained with the adaptive protocol.

Full size image

Two parameter phase estimation

Let us now consider a different scenario. The 3-modes interferometer built with two cascaded tritters proposed in this paper may be adopted to perform a two parameters estimation process, consisting of the simultaneous measurement of two optical phases. In this case, the reference φref is provided by the optical mode k1 and the phases to be measured, φ2 and φ3, correspond respectively to the optical modes k2 and k3 [see Fig. 5 (a)]. In order to evaluate the maximum precision achievable in the two parameter problem, it is necessary to extend the concept of quantum Fisher information to the multiparameter case44. Indeed, it is possible to define a quantum Fisher information matrix (QFIM) Hµν corresponding to the set of parameter λ = (λ1, …, λn), which in the pure state case is defined in terms of the set of generators G = (G1, …, Gn) for the parameters λ. The error on the single parameter λµ for a fixed value of the other parameters λν, with ν ≠ µ, is bounded by the inequality: δλµ ≥ [(H−1)µµ/M]1/2. When performing the simultaneous estimation of the set of parameters λ, the sum of the variances is bounded by the multiparameter Cramér-Rao inequality: .

Figure 5
figure 5

(a)–(b) Schemes for two parameters phase estimation with the 3- and 4-modes integrated interferometers.(c) Comparison between the effective quantum Fisher informations for the two-parameters problem when the interferometer is fed with Fock states or coherent states.

Full size image

We now consider as input state a coherent state |α〉 with 〈n〉 = 3, which defines the standard quantum limit for a N = 3 photon probe. As for the single parameter scenario, it is necessary to evaluate the quantum Fisher information matrices both (i) in presence of an external phase reference and (ii) in absence of an external phase reference . The corresponding bounds for the sensitivities after M measurements in the two cases are given by and . When a three photon state |1, 1, 1〉 is injected into the interferometer, the bounds for the parameters φ2 and φ3 are the same for both cases (i) and (ii) leading to . The same analysis may be performed in the case of a 4-modes interferometer, fed with a coherent state of 〈n〉 = 4 photons or with a Fock state |1, 1, 1, 1〉, where the two parameters are now the phases φ3 and φ4 on modes k3 and k4 [see Fig. 5 (b)]. The results are shown in Fig. 5 (c), showing that in absence of a phase reference the adoption of Fock probe states can lead to quantum enhanced performances in the measurement of two optical phases. Furthermore, in full analogy with the one parameter case, a greater advantange with respect to the classical strategies may be progressively achieved by increasing the number of modes.

In the single parameter case, the quantum Cramér-Rao bound can always be asymptotically achieved41 performing a suitable measurement and choosing the right estimator. On the contrary, in the multiparameter case the bound for the statistical errors defined by the quantum Fisher information matrix is not in general achievable45,46. This depends on the fact that the optimal measurements for the individual parameters may not be compatible observables. A necessary condition for the achievability of the multiparameter quantum Cramér-Rao bound is then given by the weak commutativity condition: Tr[ρλ[Lµ,Lν]] = 0. Here, the Lµ operators are the symmetric logarithmic derivatives (SLD), which define the optimal measurement and estimators for the individual parameters47. In our case, it can be shown that (see Supplementary Material) for the 3-mode interferometer injected by the |1, 1, 1〉 input state the operators {L2, L3} for {φ2, φ3} commute, thus satisfying the necessary condition to achieve the quantum Cramér-Rao bound. The same result holds for the 4-mode case. The next step to be investigated is the identification of suitable measurements and estimators.

Discussions

The analysis performed in this work represents the first step in the investigation of integrated quantum technology in view of the realization of multiport optical beam splitters enabling novel multiphoton sensing schemes based on 3D interferometers. We investigated the adoption of this technology to perform phase estimation protocols leading to quantum-enhanced performances. We provided and simulated a full protocol for sub-SQL phase measurements, by exploiting Fock input states and photon-counting detection, thus not requiring any post-selection for the generation of the probe state. We also discussed the application of the same multimode structure for multiparameter estimation purposes. The present technology is expected to lead to the development of new phase estimation protocols able to reach Heisenberg-limited performances31 and to open a new scenario for the simultaneous measurement of more than one optical phase. Indeed, the present approach can be adopted as an accessible test bench to investigate theoretically and experimentally the still unexplored scenario of multiparameter estimation. Further perspectives may lead to the application of this multiport splitters in other contexts, such as quantum simulations48, linear optical computing49 and nonlocality tests50.