Introduction

Long-ranged electrostatic and hydrodynamic interactions are important in many problems, from cloud formation1,2 to the nucleation and growth of crystals3,4,5. The tunable control of electrostatic interactions in colloidal systems has helped us to identify the conditions under which coherent crystalline structures6,7,8,9,10,11,12 or incoherent glass, gel and cluster phases13,14,15 form in the laboratory. However, similar tuning of hydrodynamic interactions has not yet been achieved and this is the focus of the current work.

Our experimental system is a two-component mixture of oil drops of one component inside a surrounding medium of a second oil which belongs to the class of “leaky dielectrics”16,17, where an electric field is a good control parameter for tuning the strength of hydrodynamic fields. The fundamental phenomena observed in leaky dielectrics16,18 are related to the accumulation of free charge at the oil-oil interface, which adds a tangential component to electric stresses. These tangential stresses compete with normal stresses that arise in any dielectric. The angular variation of the normal stresses on the drop gives rise to shape deformations of droplets19,20 while the magnitude of the total electric stresses determine the conditions for the break-up of drops18,19. In the presence of an oscillating electric field E of frequency f, a spherical oil drop immersed in a surrounding leaky-dielectric oil medium experiences normal and tangential electric stresses that have a steady and a time-dependent part19; the equations, which include both dipolar (internal to the drop) and hydrodynamic contributions, are reproduced in Supplementary Information. The total stress is a function of frequency (Supplementary Fig. 1) and exhibits a transition from hydrodynamics-dominated to dipolar-dominated, where in the latter regime, the tangential electric stress is zero. The time-dependent normal stresses also induce pulsating droplet shapes. The periodic volume displacement of these pulsating drops are an additional source of hydrodynamic disturbances. With increasing frequency, the spatial extent of the droplet oscillation decreases, reducing the strength of hydrodynamics.

In our system, we have numerous oil droplets (silicone oil) in a surrounding leaky-dielectric oil medium (immersion oil or castor oil). Here, there will also be collective contributions, due to droplet interactions, to both hydrodynamic and dipolar forces.

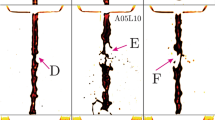
An overview of the self-organized structures we observe as a function of frequency is shown in Fig. 1. When subjected to either dc or low frequency ac fields, a large static droplet at zero field (Fig. 1a) exhibits a turbulent breakup into clouds of smaller droplets (Fig. 1b, c and Supplementary Movie 1). This strongly hydrodynamic regime is marked by highly inhomogeneous flow fields, which results in vigorous chaotic motion of the droplets within each cloud and their repeated breakup and coalescence (Fig. 1b, c). The strength of the hydrodynamic interaction decreases with increase in f, a dependence that signifies the importance of viscous damping. At frequencies above 1 Hz, there is a transition to a weaker hydrodynamic regime where drops undergo pulsating shape oscillations (Fig. 1d–f, see also Supplementary Movie 2). At 2 Hz, there are elliptical in-plane deformations (Fig. 1d), with occasional droplet breakup events being preceded by droplet coalescence (Supplementary Movie 3). Between 5 and 10 Hz, the in-plane deformations take on well-defined polygonal shapes (Fig. 1e, f) with the number of sides n taking on values from 3 to 12 in our experiments. At low packing density of droplets, deformations of a droplet are uncorrelated to those of its neighbors (Fig. 1f). At higher packings there are additional collective effects (Fig. 1e), completely unprecedented for micron-scale droplets. At frequencies between 25 and 50 Hz the pulsating droplets coalesce (Fig. 1g). Finally, at even higher frequencies ~ 1 KHz, we access the more familiar dipolar regime (Fig. 1h). Importantly, we can also utilize this frequency-dependent phase diagram in making monodisperse drops with controllable shape and ordered arrays of these drops.

Figure 1
figure 1

Overview.

a, Silicone oil drop in immersion oil in zero field. b–h, Structures seen as a function of frequency spanning hydrodynamic and dipolar regimes. The electric field is perpendicular to the plane of the page.

Full size image

Results

When exposed to d.c. fields, a large silicone oil drop immersed in immersion oil (or castor oil) breaks up into tiny droplets in a turbulent manner with waves traveling along the drop interface; this is shown in Fig. 1 (the field is turned on between (a) and (b)) and in Supplementary Movie 1. This is clearly a regime of very strong hydrodynamic interactions.

At frequencies below 1 Hz, we observe catastrophic breakup of a droplet. Figure 2a shows a sequence of images after an applied field at f = 0.5 Hz: first from spherical (or slightly prolate) to oblate, then undergoing irreversible topological transformation leading to breakup into tiny droplets. Shown in Fig. 2b (left panel) is a snapshot of a droplet cluster, with the trajectory of each droplet overlaid, above a threshold field where droplets are moving chaotically in 3 dimensions. The magnitude of the velocities of moving droplets in the plane are extracted using Particle Image Velocimetry and the rms velocity, vrms, is plotted with E2 in Fig. 2b (right panel). Figure 2b (right panel) shows that there are two thresholds: the first at E2 = 0.1(V/µm)2 is the onset of steady motion likely associated with the depinning of the droplets from the substrate, while the second at E2 = 1(V/µm)2 marks the onset of a noisier regime indicating chaotic motion which persists over long times (~ hours). This finding is at first surprising in a system with low Reynolds number (Re ~ 2 × 10−5). For a comparison, chaotic motions for Re ~ 800 have been reported by Peters et al21 for the inertial system of a single rotor in a leaky dielectric medium. One may define an electric Reynolds number, , as the ratio of the timescales of charge convection and charge relaxation22. In this expression, the parameters for the internal and the external fluids are given, respectively, as dielectric constants in and ex and conductivities σin and σex; 0 is the free space permittivity and a is the drop size. In our experiments, ReE is of order unity.

Figure 2
figure 2

Transition from strong to weak hydrodynamics.

a, Time evolution of the surface topology of a single drop at an electric field E = 5.1 V/µm and f = 0.5 Hz. The electric field is parallel to the plane of the page, pointing vertically upwards. b, Left: snapshot of a cloud of droplets with the timeline of each droplet overlaid. Right: the rms velocity vrms of moving droplets plotted against applied electric field intensity E2 during one period of oscillation (f = 0.03 Hz) exhibits two thresholds: one indicating onset of steady motion and the second, the onset of chaotic motion. c, The in-plane deformation of droplets at E = 12 V/µm and f = 1 Hz, 2 Hz and 3 Hz. In b and c, the electric field is perpendicular to the plane of the page. d, The droplets become more circular (χ more narrowly distributed near unity) as the frequency is increased from 1 to 3 Hz.

Full size image

At frequencies above 1 Hz, droplet breakup events become rarer. However, at this frequency the shape of the in-plane drop deformations is still highly non-circular, but becomes increasingly circular as f is increased to 2 and 3 Hz (Fig. 2c and Supplementary Movie 3). The circularity of the droplets is computed as χ = 4πA0/L2 where A0 is the area of the droplet and L is its perimeter, with perfect circles having χ = 1. The probability distribution function of χ, P(χ), (Fig. 2d) is strongly peaked near the value of 1 at 3 Hz, while the distribution is progressively skewed towards lower values of χ for 1 Hz. Lower χ values, arising from non-circular droplet shape deformations, directly result from spatial and temporal variations in fluid flow around the droplet, i.e. time-dependent and inhomogeneous shear. This change in droplet circularity thus signals a transition from strong to weak hydrodynamics. The transition from weak to strong hydrodynamic behaviour is continuous and is likely to be related to the continuous decrease with frequency of the hydrodynamic lengthscale, the origins of which are elaborated in the Discussion.

Upto driving frequencies of about f = 50 Hz, droplet deformations remain time dependent, taking on shapes that oscillate at the driving frequency between a sphere and an oblate spheroid, i.e. compressed along the field direction. The proximity of boundaries breaks the symmetry of the associated hydrodynamic flow fields, resulting in the migration of the droplets to one of the surfaces. For 10 < f < 50 Hz, the droplets exhibit ratchet-like motion. This mobility likely arises out of contact angle hysteresis23. Time-dependent droplet shape profiles (with electric field in the plane) at f = 3.5 Hz are shown in Supplementary Movie 2. At 5 < f < 10 Hz (an example at 7 Hz is shown in Fig. 3a, where the field points into the page) the time-dependent deformations oscillate between a sphere and an oblate spheroid. The spherical drop in our experiment has radially inward electric stresses with a magnitude that is angle-dependent and larger at the poles than at the equator (Supplementary Fig. 1). This drives it to be oblate when the field amplitude increases from zero. The amplitude of the field goes from its maximum value to zero twice per cycle and the droplet goes from oblate to spherical with the same frequency. At the same time, the in-plane shape of the drops go from circular to polygonal at the maximum amplitude of the field, where the drop is maximally oblate (see Supplementary Movie 4). We observe droplets with a number of facets n = 3 to 12. Figure 3b shows that the droplet radius an, normalized with radius for n = 3, is proportional to n. Thus, a characteristic wavelength λ = 2πan/n ≈ 12 µm is associated with this phenomenon.

Figure 3
figure 3

Pulsating polygonal droplets in the weak hydrodynamics regime.

See Supplementary Movie 4 for dynamics. a, Polygonal deformations at f = 7 Hz, E = 10 V/µm. With increasing droplet radius, the number of facets per drop increases; n = 3 to 12 are observed. The field is perpendicular to the plane of the page. b, The relationship between droplet radius normalized for n = 3 and n is roughly linear, signifying the existence of a characteristic wavelength λ. Here λ = (2π)(2 µm) ≈ 12 µm. The solid black line is obtained from Lee and McConnell25.

Full size image

Polygonal shapes in systems with inertia can arise from Rayleigh oscillations24, which is not a likely explanation for this overdamped system. Instead, we begin by considering the static forces on a maximally flattened drop. In this state, the system is similar to the system of 2-dimensional drops in binary liquid mixtures in Langmuir monolayers25, where polygonal shapes with symmetry number n are obtained from a balance of interfacial tension (which favors circularity) and dipolar repulsion (which favors large centre-periphery distances). This results in a shape dependent free energy F = Felectric + Finterfacial where and , where dR is the differential line element, µ is the difference in dipole density in the two phases, k is the effective line tension and ρ = (|R − R′|2 + δ2)0.5 with δ as a cut-off parameter. For a circular shape, one may minimize the free energy to obtain an equilibrium radius aeq, which is a function of the materials parameters (µ and k). For larger drops, the circular shape is unstable with respect to a transition to n-fold symmetry. Since we observe symmetries with n = 3 or greater, we plot a scaled droplet radius an/a3 versus the symmetry number n (thus scaling away the materials parameters). The two-dimensional model of Lee & McConnell predicts an/a3 = exp(Zn − Z3), where Zn is a complicated function of n, but may be determined numerically25. Comparing our experimental results with the model prediction, which is the solid line in Fig. 3b, we find agreement with no adjustable parameters. This indicates that this mechanism is very important. A characteristic length can be obtained in three dimensions from a balance of dipolar and surface energy. For a sphere of radius a in three dimensions, the dipolar energy is , where . The surface energy is 4πa2γ, where γ is the surface tension. Minimizing the total energy and solving for a, one obtains a lengthscale of order 100 µm. This is somewhat larger than the observed 12 µm lengthscale. This is reasonable, as it indicates that there are other (likely electrohydrodynamic) contributions to the electrical energy. In principle, parametric instabilities26,27,28 could also result in such polygonal shapes. At high packings, the morphology of the facets is highly influenced by the proximity of neighbours (Fig. 1e).

In the frequency regime between 25 and 50 Hz, we observe deformations that are much weaker in amplitude; here drop coalescence begins to dominate and droplets exhibit ratchetlike motions (Fig. 1g and Supplementary Movie 5). Droplet motions can be induced by other means, for example via surface tension gradients that are induced by thermal gradients29 or by particles consuming energy and becoming “self-mobile” active particles30. This regime provides an additional mechanism for external control of particle activity. Both ratcheting and coalescence stop abruptly (due to viscous effects in a low Reynolds number regime) when the field is turned off.

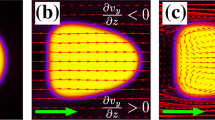
Above 50 Hz, the droplets do not pulsate between spherical and oblate and we see a time-averaged shape. For further understanding, we quantify the frequency dependence of droplet shapes. The droplet shape in an electric field is prolate, i.e. elongated along the field direction, in a pure dielectric medium, while in a conducting medium it is oblate, due to tangential electric stresses in the presence of electric-field driven flows16,17. If the initially spherical droplet, radius a, is deformed into a spheroid with dimensions d|| and d⊥ parallel and perpendicular to the external field respectively, the deformation . We may write a scaled deformation . In our experiments, we find that the droplet shape changes from oblate (Dscaled < 0) to spherical (Dscaled = 0) to prolate (Dscaled > 0) as a function of frequency (Fig. 4a–c), with a crossover, shown in Fig. 4d, at fc = 100 Hz. The charge relaxation time scale τc is given by . Thus fc ~ 1/τc, which is consistent with the leaky dielectric model16,17,31. The theoretical expression19 (solid red line) which is only valid in the regime of steady-state droplets shows qualitatively the same trend. Details of the impedance measurements made to determine the conductivities are provided in Supplementary Fig. 2.

Figure 4
figure 4

Transition from hydrodynamic to dipolar.

A frequency driven transition from oblate (electrohydrodynamics dominated) to prolate (dipolar dominated) droplet deformation is observed. Shown is a droplet that is a, oblate at 70 Hz, b, spherical at 100 Hz and c, prolate at 1 KHz. In a–c, the field is parallel to the plane of the page and pointing vertically upwards. d, The scaled deformation Dscaled, plotted with frequency f for different sized drops shown by different colored circles, collapses onto a single curve, qualitatively consisent with a theoretical expression for static droplets19 (solid red line). Variation with f of the hydrodynamic length lh (solid black line). A frequency quench from the hydrodynamic regime (large lh, negative D) towards the dipolar regime (small lh) is used to make monodisperse droplet arrays of controllable shape. Micrographs obtained in e, strong hydrodynamic regime at f = 0.5 Hz (lh ~ 1 mm), f, weak hydrodynamic regime at f = 25 Hz (lh ~ 25 µm) and g, dipolar regime at f = 1 KHz (lh ~ 0.5 µm). In e–g, the field is perpendicular to the plane of the page.

Full size image

Discussion

The frequency f affects not only the strength of the hydrodynamic interaction but also the lengthscale. The ion drift velocity vd = µE, where µ is the electric mobility. In a time τh = 1/f, the ions have drifted a distance lh = vd/f. The hydrodynamic length lh, shown in Fig. 4d (solid black line), ranges from 300 µm at f = 2 Hz to 6 µm at f = 100 Hz. We can vary this lengthscale from millimeters, where we see turbulent behaviour (Fig. 4e), to tens of micrometers, where we observe droplets coalescence (Fig. 4f), to micrometers, where we access the dipolar regime (Fig. 4g). Further control of this lengthscale and the corresponding droplet regime by replacing the outer fluid with the more viscous castor oil is shown in Supplementary Fig. 3. While the stress on a single spherical drop can be written down, the real situation is more complicated by two factors. First, the droplet shape changes due to the time-dependent normal stresses and the unbalanced tangential stresses and this is an additional source of hydrodynamic disturbances. Second, the dynamics of droplets also depends on the modification of flow fields around a droplet due to neighbouring droplets. The lengthscale of these droplet-droplet correlations is the above hydrodynamic lengthscale.

The frequency-dependent self organization described above makes for some very interesting potential applications. Static (non-pulsating) oblate or prolate shapes are obtained above 50 Hz and both below and above the crossover frequency fc = 100 Hz. This allows the occurrence of both oblate and prolate steady-state droplets. First, we find that the route to droplet breakup (quenching from f = 3 Hz to 1 Hz) can be utilized to produce monodisperse droplet arrays. A subsequent frequency quench into the time-independent regime (where dipolar interactions are quantitatively more important) immobilizes these droplets; a schematic of this strategy is shown in Fig. 4d. Shown in Fig. 5a and b is a droplet array at 70 Hz (oblate droplets) and 1 KHz (prolate droplets). There is a similar array on the other substrate, separated by 90 µm (darker, out-of-focus structures). Both are composed of monodisperse droplets (polydispersity ~ 7%) that have an equilibrium in-plane spacing of about 40 µm. At high frequencies, the large distance interactions of these droplets is repulsive primarily due to dipolar interactions. The FFTs of these droplets array display weak hexagonal ordering, shown in the bottom insets of Fig. 5a and b.

Figure 5
figure 5

Droplet array.

a, At 70 Hz, each droplet in the array is a section of an oblate spheroid. The top inset shows the droplet acting as a lens for the bottom layer of droplets, see text. b, At 1 KHz, each droplet is a section of a prolate spheroid. The FFTs in the bottom insets of (a, b) display weak hexagonal ordering. The field is perpendicular to the plane of the page.

Full size image

The top inset to Fig. 5a shows a single droplet on the top substrate (slightly defocussed). The symmetry of intensity within the droplet in every case is that of 3 droplets on the bottom surface, indicating a simple lensing effect. It is apparent that what we have is an array of microlenses (numerical aperture of 0.3) whose shape is controllable by varying frequency.

In summary, we have demonstrated fine control over frequency-dependent hydrodynamics in an oil-in-oil system. Such control will enable us to address challenging problems in nature where many-body electrostatic and hydrodynamic interactions are important.

Methods

A silicone oil (Dow Corning, dielectric constant , conductivity σin = 3.6 × 10−10 S/m and viscosity ηin = 0.38 Pa.s) droplet suspended in immersion oil (Immersol 518F, Zeiss, , σex = 4.6 × 10−9 S/m and ηex = 0.36 Pa.s) is placed between two electrodes and a sinusoidal a.c. voltage (amplitude: 0–2 KV and frequency: 1 mHz–1 KHz) is applied. Two sample geometries are used. In the vertical geometry, two ITO electrodes are separated by 100 µm thick glass spacers and the electric field is perpendicular to the plane of the substrate. In the horizontal geometry, two 130 µm thick stainless steel electrodes are placed side by side with a spacing of 350 µm and the field is parallel to the plane of the substrate. The system is sealed with ultraviolet curing adhesive and imaged via a bright field microscope and a high speed camera (PCO) with frame rates ranging from 100 to 1000 fps. Experiments are also carried out with silicone oil with ηin = 1 Pa.s and castor oil with ηex = 0.72 Pa.s.

Interfacial tension γ is measured in situ. When the field is turned on or off, the droplet relaxes to its equilibrium shape (Supplementary Fig. 4). This shape relaxation is exponential in time; the time constant τγ = (ηex+ηin)a/γ arises from a balance of viscous and interfacial stresses32. Obtaining τγ/a experimentally for 45–70 µm droplets, we find γ = 2 mN/m in silicone oil/immersion oil and 3 mN/m in silicone oil/castor oil (±0.1 mN/m).