Introduction

Nonlocality is arguably among the most striking aspects of quantum mechanics, defying our intuition about space and time in a dramatic way1. Although this feature was initially regarded as evidence of the incompleteness of the theory2, there is today overwhelming experimental evidence that nature is indeed nonlocal3. Moreover, nonlocality plays a central role in quantum information science, where it proves to be a powerful resource, allowing, for instance, for the reduction of communication complexity4 and for device-independent information processing5,6,7,8.

In a quantum Bell test, two (or more) parties perform local measurements on an entangled quantum state, Fig. 1(a). After accumulating enough data, both parties can compute their joint statistics and assess the presence of nonlocality by checking for the violation of a Bell inequality. Although entanglement is necessary for obtaining nonlocality it is not sufficient. First, there exist some mixed entangled states that can provably not violate any Bell inequality since they admit a local model9,10. Second, even for sufficiently entangled states, one needs judiciously chosen measurement settings11. Thus although nonlocality reveals the presence of entanglement in a device-independent way, that is, irrespectively of the detailed functioning of the measurement devices, one generally considers carefully calibrated and aligned measuring devices in order to obtain a Bell inequality violation. This in general amounts to having the distant parties share a common reference frame and well calibrated devices.

Figure 1
figure 1

Bell violations with random measurements.

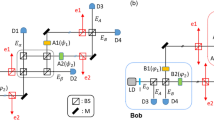
(a) Schematic representation of a Bell test. (b) Schematic of the integrated waveguide chip used to implement the new schemes described here. Alice and Bob's measurement circuits consist of waveguides to encode photonic qubits, directional couplers that implement Hadamard-like operations, thermal phase shifters to implement arbitrary measurements and detectors.

Full size image

Although this assumption is typically made implicitly in theoretical works, establishing a common reference frame, as well as aligning and calibrating measurement devices in experimental situations are never trivial issues. For instance, in the context of quantum communications via optical fibres, unavoidable small temperature changes induce strong rotations of the polarisation of photons in the fibre. This makes it challenging to maintain a good alignment, which in turn severely hinders the performance of quantum communication protocols in optical fibres12. Also, in the field of satellite based quantum communications13,14, the alignment of a reference frame represents a key issue given the fast motion of the satellite and the short amount of time available for completing the protocol—in certain cases there simply might not be enough time to align a reference frame. Finally, in integrated optical waveguide chips, the calibration of phase shifters is a cumbersome and time-consuming operation. As the complexity of such devices is increased, this calibration procedure will become increasingly challenging.

It is therefore an interesting and important question whether the requirements of having a shared reference frame and calibrated devices can be dispensed with in nonlocality tests. It was recently shown15 that, for Bell tests performed in the absence of a shared reference frame, i.e., using randomly chosen measurement settings, the probability of obtaining quantum nonlocality can be significant. For instance, considering the simple Clauser-Horne-Shimony-Holt (CHSH) scenario16, randomly chosen measurements on the singlet state lead to a violation of the CHSH inequality with probability of ~ 28%; moreover this probability can be increased to ~ 42% by considering mutually unbiased measurement bases. The generalisation of these results to the multipartite case were considered in Refs.15,17, as well as schemes based on decoherence-free subspaces18. Although these works demonstrate that nonlocality can be a relatively common feature of entangled quantum states and random measurements, it is of fundamental interest and practical importance to establish whether Bell inequality violation can be ubiquitous.

Here we demonstrate that nonlocality is in fact a far more generic feature than previously thought, violating CHSH inequalities without a shared frame of reference and even with uncalibrated devices, with near-certainty. We first show that whenever two parties perform three mutually unbiased (but randomly chosen) measurements on a maximally entangled qubit pair, they obtain a Bell inequality violation with certainty—a scheme that requires no common reference frame between the parties, but only a local calibration of each measuring device. We further show that when all measurements are chosen at random (i.e., calibration of the devices is not necessary anymore), although Bell violation is not obtained with certainty, the probability of obtaining nonlocality rapidly increases towards one as the number of different local measurements increases. We perform these random measurements on the singlet state of two photons using a reconfigurable integrated waveguide circuit, based on voltage-controlled phase shifters. The data confirm the near-unit probability of violating an inequality as well as the robustness of the scheme to experimental imperfections—in particular the non-unit visibility of the entangled state—and statistical uncertainty. These new schemes exhibit a surprising robustness of the observation of nonlocality that is likely to find important applications in diagnostics of quantum devices (e.g. removing the need to calibrate the reconfigurable circuits used here) and quantum information protocols, including device-independent quantum key distribution5 and other protocols based on quantum nonlocality6,7,8 and quantum steering19.

Results

Bell test using random measurement triads

Two distant parties, Alice and Bob, share a Bell state. Here we will focus on the singlet state

though all our results can be adapted to hold for any two-qubit maximally entangled state. Let us consider a Bell scenario in which each party can perform 3 possible qubit measurements labelled by the Bloch vectors and (x, y = 1, 2, 3) and where each measurement gives outcomes ±1. After sufficiently many runs of the experiment, the average value of the product of the measurement outcomes, i.e. the correlators , can be estimated from the experimental data. In this scenario, it is known that all local measurement statistics must satisfy the CHSH inequalities:

and their equivalent forms where the negative sign is permuted to the other terms and for different pairs x, x′ and y, y′; there are, in total, 36 such inequalities.

Interestingly, it turns out that whenever the measurement settings are mutually unbiased, i.e. and (orthogonal measurement triads, from now on simply referred to as measurement triads), then at least one of the above CHSH inequalities must be violated — except for the case where the measurement triads are perfectly aligned, i.e. for each x, there is a y such that . Therefore, a generic random choice of unbiased measurement settings — where the probability that Alice and Bob's settings are perfectly aligned is zero (for instance if they share no common reference frame) — will always lead to the violation of a CHSH inequality.

Proof. Assume that and are orthonormal bases. Since the correlators of the singlet state have the simple scalar product form , the matrix

contains (in each column) the coordinates of the three vectors , written in the basis .

By possibly permuting rows and/or columns and by possibly changing their signs (which corresponds to relabelling Alice and Bob's settings and outcomes), we can assume, without loss of generality, that E11, E22 > 0 and that E33 > 0 is the largest element (in absolute value) in the matrix . Noting that and therefore |E33| = |E11E22 – E12E21|, these assumptions actually imply E33 = E11E22 – E12E21 ≥ E11, E22, |E12|, |E21| and E12E21 ≤ 0; we will assume that E12 ≤ 0 and E21 ≥ 0 (one can multiply both the x = 2 row and the y = 2 column by −1 if this is not the case).

With these assumptions, (E11 + E21) max[–E12, E22] ≥ E11E22 – E12E21 = E33 ≥ max[–E12, E22] and by dividing by max[–E12, E22] > 0, we get E11 + E21 ≥ 1. One can show in a similar way that –E12 + E22 ≥ 1. Adding these last two inequalities, we obtain

Since is an orthogonal matrix, one can check that equality is obtained above (which requires that both E11 + E21 = 1 and –E12 + E22 = 1) if and only if , and . (See Supplementary Information for details) Therefore, if the two sets of mutually unbiased measurement settings and are not aligned, then inequality (4) is strict: a CHSH inequality is violated. Numerical evidence suggests that the above construction always gives the largest CHSH violation obtainable from the correlations (3).

While the above result shows that a random choice of measurement triads will lead to nonlocality with certainty, we still need to know how these CHSH violations are distributed; that is, whether the typical violations will be rather small or large. This is crucial especially for experimental implementations, since in practise, various sources of imperfections will reduce the strength of the observed correlations. Here we consider two main sources of imperfections: limited visibility of the entangled state and finite statistics.

First, the preparation of a pure singlet state is impossible experimentally due to noise. In the experiment described here, limited visibility mainly originates from imperfect operation of the photon source and detectors. It is thus desirable to understand the effect of such experimental noise, which can be modelled by a Werner state with limited visibility V:

This, in turn, results in the decrease of the strength of correlations by a factor V. In particular, when , the state (5) ceases to violate the CHSH inequality. States ρV are known as Werner states9.

Second, in any experiment the correlations are estimated from a finite set of data, resulting in an experimental uncertainty. To take into account this finite-size effect, we will consider a shifted classical bound of the CHSH expression (2) such that an observed correlation is only considered to give a conclusive demonstration of nonlocality if . Thus, if the CHSH value is estimated experimentally up to a precision of δ, then considering a shifted classical bound of ensures that only statistically significant Bell violations are considered.

We have estimated numerically the distribution of the CHSH violations (the maximum of the left-hand-side of (2) over all x, x′, y, y′) for uniformly random measurement triads on the singlet state (see Fig. 2). Interestingly, typical violations are quite large; the average CHSH value is ~ 2.6, while only ~ 0.3% of the violations are below 2.2. Thus this phenomenon of generic nonlocality is very robust against the effect of finite statistics and of limited visibility, even in the case where both are combined. For instance, even after raising the cutoff to and decreasing the singlet visibility to V = 0.9, our numerical simulation shows that the probability of violation is still greater than 98.2% (see Fig 2).

Figure 2
figure 2

(a) Bell tests using random measurement triads (theory).

Distribution of the (maximum) CHSH violations for uniformly random measurement triads on a singlet state. The inset shows the probability of obtaining a CHSH violation as a function of the visibility V of the Werner state; this probability is obtained by integrating the distribution of CHSH violations (main graph) over the interval . (b) Bell tests using completely random measurements (theory). Plot of the probability of Bell violation as a function of the visibility V of the Werner state, for different numbers m of (completely random) measurements per party.

Full size image

Bell tests using completely random measurements

Although performing unbiased measurements does not require the spatially separated parties to share a common reference frame, it still requires each party to have good control of the local measurement device. Clearly, local alignment errors (that is, if the measurements are not exactly unbiased) will reduce the probability of obtaining nonlocality. In practise the difficulty of correctly aligning the local measurement settings depends on the type of encoding that is used. For instance, using the polarisation of photons, it is rather simple to generate locally a measurement triad, using wave-plates. However, for other types of encoding, generating unbiased measurements might be much more complicated (see experimental part below).

This leads us to investigate next the case where all measurement directions are chosen randomly and independently. For simplicity, we will focus here on the case where all measurements are chosen according to a uniform distribution on the Bloch sphere. Although this represents a particular choice of distribution, we believe that most random distributions that will naturally arise in an experiment will lead to qualitatively similar results, as indicated by our experimental results.

We thus now consider a Bell test in which Alice and Bob share a singlet and each party can use m possible measurement settings, all chosen randomly and uniformly on the Bloch sphere. We estimated numerically the probability of getting a Bell violation as a function of the visibility V [of the state (5)] for m = 2,…,8; see Fig. 2. Note that for m ≥ 4, additional Bell inequalities appear20; we have checked however, that ignoring these inequalities and considering only CHSH leads to the same results up to a very good approximation. Fig. 2 clearly shows that the chance of finding a nonlocal correlation rapidly increases with the number of settings m. Intuitively, this is because when choosing an increasing number of measurements at random, the probability that at least one set of four measurements (2 for Alice and 2 for Bob) violates the CHSH inequality increases rapidly. For example, with m = 3 settings, this probability is 78.2% but with m = 4, it is already 96.2% and for m = 5 it becomes 99.5%. Also, as with the case of unbiased measurements, the probability of violation turns out to be highly robust against depolarising noise; for instance, for V = 0.9 and m ≥ 5, there is still at least 96.9% chance of finding a subset among our randomly chosen measurements that gives nonlocal correlations.

Measurement devices

We use the device shown in Fig. 1(b) to implement Alice and Bob's random measurements on an entangled state of two photons. This device is a reconfigurable quantum photonic chip, in which qubits are encoded using path or dual-rail encoding25. The path encoded singlet state is generated from two unentangled photons using an integrated waveguide implementation21,22 of a nondeterministic cnot gate23, an architecture which also enables deliberate introduction of mixture. This state is then shared between Alice and Bob who each have a Mach-Zehnder (MZ) interferometer, consisting of two directional couplers (equivalent to beamsplitters) and variable phase shifters ( and ) and single photon detectors. This enables Alice and Bob to independently make a projective measurement in any basis by setting their phase shifters to the required values24,25. The first phase-shifters () implement rotations around the Z axis of the Bloch sphere (); since each directional coupler implements a Hadamard-like operation (, where H is the usual Hadamard gate), the second phase shifters () implement rotations around the Y axis (). Overall, each MZ interferometer implements the unitary transformation U(, ) = RY()RZ(), which enables projective measurement in any qubit basis when combined with a final measurement in the logical (Z) basis using avalanche photodiode single photon detectors (APDs).

Each thermal phase shifter is implemented as a resistive element, lithographically patterned onto the surface of the waveguide cladding. Applying a voltage v to the heater has the effect of locally heating the waveguide, thereby inducing a small change in refractive index n (dn/dT ≈ 1 × 10–5K) which manifests as a phase shift in the MZ interferometer. There is a nonlinear relationship between the voltage applied and the resulting phase shift (v), which is generally well approximated by a quadratic relation of the form

In general, each heater must be characterised individually — a procedure which is both cumbersome and timeconsuming. The function (v) is estimated by measuring single-photon interference fringes from each heater. The parameter α can take any value between 0 and 2π depending on the fabrication of the heater, while typically 24,25. For any desired phase, the correct voltage can then be determined.

In the experiments described here, heater calibration is necessary both for state tomography and for implementing random measurement triads. In contrast, this calibration can be dispensed with entirely when implementing completely random measurements. Thus, in this case we simply choose random voltages from a uniform distribution, in the range [0V, 7V], which is adequate to address phases in the range no a priori calibration of Alice and Bob's devices is necessary. Clearly this represents a significant advantage for our device.

Experimental violations with random measurement triads

We first investigate the situation in which Alice and Bob both use 3 orthogonal measurements. We generate randomly chosen measurement triads using a pseudo-random number generator. Having calibrated the phase/voltage relationship of the phase shifters, we then apply the corresponding voltages on the chip. For each pair of measurement settings, the two-photon coincidence counts between all 4 combinations of APDs (C00, C01, C10, C11) are then measured for a fixed amount of time—the typical rate of simultaneous photon detection coincidences is ~ 1 kHz. From these data we compute the maximal CHSH value as detailed above. This entire procedure is then repeated 100 times. The results are presented in Fig. 3a, where accidental coincidences, arising primarily from photons originating from different down-conversion events, which are measured throughout the experiment, have been subtracted from the data (the raw data, as well as more details on accidental events, can be found in the Methods). Remarkably, all 100 trials lead to a clear CHSH violation; the average CHSH value we observe is ~ 2.45, while the smallest measured value is ~ 2.10.

Figure 3
figure 3

Bell tests requiring no shared reference frame.

Here we perform Bell tests on a two-qubit Bell state, using randomly chosen measurement triads. Thus our experiment requires effectively no common reference frame between Alice and Bob. (a) 100 successive Bell tests; in each iteration, both Alice and Bob use a randomly-chosen measurement triad. For each iteration, the maximal CHSH value is plotted (black points). In all iterations, we get a CHSH violation; the red line indicates the local bound (CHSH = 2). The smallest CHSH value is ~ 2.1, while the mean CHSH value (dashed line) is ~ 2.45. This leads to an estimate of the visibility of , to be compared with 0.913 ± 0.004 obtained by maximum likelihood quantum state tomography28. (See Supplementary Information for further discussion of this slight discrepancy.) Error bars, which are too small to draw, were estimated using a Monte Carlo technique, assuming Poissonian photon statistics. (b) The experiment of (a) is repeated for Bell states with reduced visibility, illustrating the robustness of the scheme. Each point shows the probability of CHSH violation estimated using 100 trials. Uncertainty in probability is estimated as the standard error. Visibility for each point is estimated by maximum-likelihood quantum state tomography, where the error bar is calculated using a Monte Carlo approach, again assuming Poissonian statistics. Red points show data corrected for accidental coincidences (see Methods), the corresponding uncorrected data is shown in blue. The black line shows the theoretical curve from Fig. 2 (inset). Further discussion of the slight discrepancy between experimental and theoretical probabilities of CHSH violation is provided in the Supplementary Information.

Full size image

We next investigate the effect of decreasing the visibility of the singlet state: By deliberately introducing a temporal delay between the two photons arriving at the cnot gate, we can increase the degree of distinguishability between the two photons. Since the photonic cnot circuit relies on quantum interference26 a finite degree of distinguishability between the photons results in this circuit implementing an incoherent mixture of the CNOT operation and the identity operation27. By gradually increasing the delay we can create states ρV with decreasing visibilities. For each case, the protocol described above is repeated, which allows us to estimate the average CHSH value (over 100 trials). For each case we also estimate the visibility via maximum likelihood quantum state tomography. Figure 3b clearly demonstrates the robustness of our scheme, in good agreement with theoretical predictions: a considerable amount of mixture must be introduced in order to significantly reduce the probability of obtaining a CHSH violation.

Together these results show that large Bell violations can be obtained without a shared reference frame even in the presence of considerable mixture.

Experimental violations with completely random measurements

We now investigate the case where all measurements are chosen at random. The procedure is similar to the first experiment, but we now apply voltages chosen randomly from a uniform distribution and independently for each measurement setting. Thus our experiment requires no calibration of the measurement MZ interferometers (i.e. the characterisation of the phase-voltage relation), which is generally a cumbersome task. By increasing the number of measurements performed by each party (m = 2, 3, 4, 5), we obtain CHSH violations with a rapidly increasing probability, see Fig. 4. For m = 5, we find 95 out of 100 trials lead to a CHSH violation. The visibility V of the state used for this experiment was measured using state tomography to be 0.869 ± 0.003, clearly demonstrating that robust violation of Bell inequalities is possible for completely random measurements.

Figure 4
figure 4

Experimental Bell tests using uncalibrated devices.

We perform Bell tests on a two-qubit Bell state, using uncalibrated measurement interferometers, that is, using randomly-chosen voltages. For m = 2, 3, 4, 5 local measurement settings, we perform 100 trials (for each value of m). As the number of measurement settings m increases, the probability of obtaining a Bell violation rapidly approaches one. For m ≥ 3, the average CHSH value (dashed line) is above the local bound of CHSH = 2 (red line). Error bars, which are too small to draw, were estimated by a Monte Carlo technique, assuming Poissonian statistics. Data has been corrected for accidentals (see Methods).

Full size image

It is interesting to note that the relation between the phase and the applied voltage is typically quadratic, see Eq. (6). Thus, by choosing voltages from a uniform distribution, the corresponding phase distribution is clearly biased. Our experimental results indicate that this bias has only a minor effect on the probability of obtaining nonlocality.

Discussion

Bell tests provide one of the most important paths to gaining insight into the fundamental nature of quantum physics. The fact that they can be robustly realised without the need for a shared reference frame or calibrated devices promises to provide new fundamental insight. In the future it would be interesting to investigate these ideas in the context of other Bell tests, for instance considering other entangled states or in the multipartite situation (see29 for recent progress in this direction), as well as in the context of quantum reference frames30,31.

The ability to violate Bell inequalities with a completely uncalibrated device, as was demonstrated here, has important application for the technological development of quantum information science and technology: Bell violations provide an unambiguous signature of quantum operation and the ability to perform such diagnostics without the need to first perform cumbersome calibration of devices should enable a significant saving in all physical platforms. These ideas could be particularly helpful for the characterisation of entanglement sources without the need for calibrated and aligned measurement devices. They could also be relevant to quantum communications experiments based on optical fibres or earth-satellite links, in which the alignment of a reference frame is cumbersome.

Finally Bell violations underpin many quantum information protocols and therefore, the ability to realise them with dramatically simplified device requirements holds considerable promise for simplifying the protocols themselves. For example, device-independent quantum key distribution5 allows two parties to exchange a cryptographic key and, by checking for the violation of a Bell inequality, to guarantee its security without having a detailed knowledge of the devices used in the protocol. Such schemes, however, do typically require precise control of the apparatus in order to obtain a sufficiently large violation. In other words, although a Bell inequality violation is an assessment of entanglement that is device-independent, one usually needs carefully calibrated devices to obtain such a violation. The ability to violate Bell inequalities without these requirements could dramatically simplify these communication tasks. The implementation of protocols based on quantum steering19 may also be simplified by removing calibration requirements.

Note added. While completing this manuscript, we became aware of an independent proof of our theoretical result on Bell tests with randomly chosen measurement triads, obtained by Wallman and Bartlett29, after one of us mentioned numerical evidence of this result to them.

Methods

Photon counting and accidentals

In our experiments, we postselect on successful operation of the linear-optical cnot gate by counting coincidence events, that is, by measuring the rate of coincidental detection of photon pairs. Single photons are first detected using silicon avalanche photodiodes (APDs). Coincidences are then counted using a Field-Programmable Gate Array (FPGA) with a time window of ~ 5 ns. We refer to these coincidence events as .

Accidental coincidences have two main contributions: first, from photons originating from different down-conversion events arriving at the detectors within the time window; second, due to dark counts in the detectors. Here we directly measure the (dynamic) rate of accidental coincidences in real time, for the full duration of all the experiments described here. To do so, for each pair of detectors we measure a second coincidence count rate, namely , with |t1 – t0| = 30 ns. In order to do this, we first split (duplicate) the electrical TTL pulse from each detector into two BNC cables. An electrical delay of 30 ns is introduced into one channel and coincidences (i.e. at ) are then counted directly. Finally we obtain the corrected coincidence counts by subtracting coincidence counts at from the raw coincidence counts at .

All experimental results presented in the main text have been corrected for accidentals. Here we provide the raw data. Fig. 5 presents the raw data for Fig. 3(a) while Fig. 6 presents the raw data for Fig. 4. Notably, in Fig. 5, corresponding to the case of randomly chosen triads, all but one of the hundred trials feature a CHSH violation. The average violation is now ~ 2.3.

Figure 5
figure 5

Raw data of experimental Bell tests requiring no shared reference frame.

This figure shows the raw data, without correcting for accidental coincidences, of Fig. 4a. Here the average CHSH value is 2.30 (dashed line), leading to an estimate of the visibility of , while the estimate from quantum state tomography is V = 0.861 ± 0.003 (see Supplementary Information). Error bars, which are too small to draw, were estimated using a Monte-Carlo technique, assuming Poissonian photon statistics.

Full size image
Figure 6
figure 6

Raw data of experimental Bell tests using uncalibrated measurement interferometers (random voltages).

This figure shows the raw data, without correcting for accidental coincidences, of Fig. 5. Error bars, which are too small to draw, are estimated by a Monte Carlo technique, assuming Poissonian statistics. The visibility V of the state used for this experiment was measured using state tomography to be 0.804 ± 0.003.

Full size image