Introduction

In mesoscopic reaction systems the copy numbers of the reacting molecules are low enough for molecular discreteness to become relevant. This induces intrinsic noise and replaces the deterministic kinetics by a stochastic model, potentially leading to quantitative and qualitative differences in the system behavior.

Oscillatory chemical reaction networks are appealing systems to study as they can exhibit a wide range of complex behaviors, such as bifurcations, limit cycles and chaos in different parts of their phase spaces. Consequently, they have been shown to be involved in a number of fundamental phenomena, including pattern formation1, turbulence2,3, chemical waves3 and vortex dynamics4. Chemical oscillators also play important roles in biological systems, ranging from circadian clocks5,6 to rhythmic gene expression and metabolism7, glycolytic oscillators8, embryonic segmentation clocks9 and cell-division control in both space and time10,11,12.

Oscillatory chemical reaction networks have traditionally been studied using deterministic, macroscopic reaction rate equations (RRE) in the form of ordinary differential equations. While this enables the application of a wealth of bifurcation and stability analysis tools from dynamical systems theory, it is only valid in the limit of large numbers of molecules, which typically requires that the reactions progress in a reactor of large (macroscopic) volume13,14,15. If the reactions are confined to smaller (mesoscopic) volumes, such as intracellular organelles, nano-reactors, or porous foams, the number of reactive molecules within any well-mixed subspace is typically too small for RRE to be generally valid. In these regimes, molecular discreteness and hence intrinsic noise, needs to be accounted for. It has been shown in numerous studies that intrinsic noise can lead to non-trivial chemical kinetics that cannot be predicted by RRE15,16,17,18,19,20,21.

The effect of intrinsic noise manifests itself differently in different types of chemical reaction networks: In linear reaction networks RRE predictions of the mean concentrations are always correct, regardless of the reactor volume14. In nonlinear reaction networks, however, noise induces quantitative differences from the concentrations predicted by RRE14,15. A fingerprint of these differences is the relaxation kinetics of the steady-state concentration fluctuations22. In monostable nonlinear systems, the relaxation kinetics of the concentration fluctuations around a non-equilibrium steady state is altered by intrinsic noise through an increase in the lifetimes of species that are reactants in any nonlinear reaction22. In frequency space, this corresponds to an increase in the bandwidth of the concentration fluctuation spectrum with increasing intrinsic noise. This quantitative difference can become large enough to render RRE invalid in certain regimes20. In multi-stable systems, intrinsic noise can lead to switching behavior between the multiple fixed points of the system14,15. This phenomenon has been used to explain spontaneous switching behavior in biochemical systems23,24,25 and the switching of gene-expression patterns in response to environmental changes26. More remarkably, intrinsic noise can induce oscillatory behavior at steady state, even when the corresponding RRE are away from Hopf bifurcation and hence do not exhibit oscillatory behavior27,21. This has, e.g., been used to explain circadian rhythms in biological organisms28,5,6.

Analysis and prediction of noise-induced effects in multi-stable and oscillatory systems is impeded by the fact that many analytical methods, such as van Kampen's system-volume expansion15 or the effective mesoscopic rate equations (EMRE)29, are limited to asymptotically (in a Lyapunov sense) monostable systems15. Consequently, understanding mesoscopic oscillatory systems requires other theoretical approaches, such as the stochastic normal form equations30, Gaussian approximation methods31, the Mori-Zwanzig projection method32, or the Hamilton-Jacobi method33,34. These methods have been used to understand stochastic fluctuations around a limit cycle in the weak-noise limit and they have led to a wealth of results about the radius of the limit cycle, correlation times and the minimum number of molecules required for sustained time-correlated oscillations.

All these approaches are based on approximations of the chemical master equation (CME)35, which governs the stochastic kinetics of chemical reaction networks in mesoscopic and macroscopic volumes. While analytically intractable, the CME renders these systems amenable to simulation studies by numerically sampling trajectories from the exact solution of the CME using an exact stochastic simulation algorithm (SSA)36. These algorithms are exact in the sense that they reproduce the correct fluctuation spectrum of the species concentrations to arbitrarily high order.

In this paper, we use an exact SSA and a mesoscopic oscillatory model system away from Hopf bifurcation to characterize the effect of intrinsic noise on the frequency spectrum of the steady-state concentration fluctuations. Extending previous work on monostable systems22, we study the fingerprints of noise in the frequency spectrum of the stochastic chemical oscillations as a function of the magnitude of intrinsic noise. For this, we study the fluctuation–relaxation kinetics of the concentrations of species in an open, mesoscopic chemical model system. We use Gillespie's original exact SSA36 to sample trajectories governed by the corresponding CME. The impact of noise is quantified by changes in the power spectral density (PSD) of the concentration fluctuations at a non-equilibrium steady state. Larger intrinsic noise is realized by decreasing the reactor volume Ω at constant mean concentration, hence decreasing the total number of reactive molecules in the system. We observe that the PSD has a Lorentzian-like form, confirming an earlier study30. Further, we show that the frequency at which the PSD is maximum depends on the reactor volume and hence the noise magnitude. We observe that the peak shifts toward lower frequencies with increasing intrinsic noise. This shift is also accompanied by an increase in bandwidth of the fluctuation spectrum, similar to the observation in monostable systems22.

Interactions between several oscillatory systems may lead to non-trivial effects37. We hence also study cascades of downstream-coupled mesoscopic chemical systems and compare the results to a single-stage system and to the linear-noise regime38,15. We show that due to intrinsic noise, each cascade stage further amplifies the shift in the peak of the PSD toward lower frequencies. For a fixed volume, the bandwidth decreases along the cascade, rendering the peak sharper and more relevant with every additional stage. In biology, downstream-coupled cascades of reaction networks are found, e.g., as cascades of autocatalytic reactions or in signaling cascades. This includes the up to six downstream-coupled autocatalytic stages of MAPK signaling cascades39,40, which can exhibit oscillatory behavior under global feedback41. Another example of an oscillatory autocatalytic biochemical system is found in cell cycle control11,12.

We believe that our findings shed light on the effect of intrinsic noise on mesoscopic oscillatory chemical reaction systems. We show that intrinsic noise can not only induce oscillatory behavior in systems away from Hopf bifurcation27,21, but that it also alters the frequency spectrum of the oscillations. The key novelty in our findings is the shift of the peak of the Lorentzian-like PSD with increasing intrinsic noise. Our findings can be used to understand the fundamental effects of intrinsic noise in (cascades of) mesoscopic chemical reaction networks. Furthermore, it has been shown that steady-state fluctuation spectra can aid parameter identification of stochastic chemical reaction networks42. Under this premise, our results can be used to more reliably identify the parameters of mesoscopic chemical reaction networks by using the corrected fluctuation–relaxation kinetics as an additional fingerprint of the effects of intrinsic noise, where the time series of steady-state fluctuations can, e.g., be obtained using fluorescence correlation spectroscopy (FCS)43,44,45.

Results

Model

We consider a chain of dowstream-coupled Brusselators38 in a reactor of volume Ω (see Fig. 1) as a model system. The Brusselator is a model system for autocatalytic reactions. Examples of autocatalytic reactions include the Belousov-Zhabotinsky reaction, MAPK signaling cascades39,40 and activation of the M-phase promoting factor in cell-cycle control11,12. The reaction network of our model system is:

where n denotes the stage of the cascade and N ≥ 1 the total number of stages. The k's are the macroscopic reaction rates. Each stage n ≥ 1 involves reactions between two species, X n and Y n . The first stage of the cascade is driven by a buffer (species X0) whose concentration is fixed at all times. Every subsequent stage of the cascade is driven by species X n−1 of the previous stage. Therefore, the first stage n = 1 is independent of the subsequent downstream stages (n > 1). In general, any stage n = q is independent of all the subsequent downstream stages (n > q).

Figure 1
figure 1

Illustration of the model system of a cascade of N downstream-coupled Brusselators.

The cascade of Brusselator reactions progresses in a mesoscopic reactor volume Ω.

Full size image

The CME corresponding to the reaction system in Eq. 1 is given by

where Xn and Yn are the populations (copy numbers) of species X n and Y n , respectively, x0 is the concentration of the buffer X0, P(Xn ,Yn ) is the probability of having Xn molecules of species X n and Yn molecules of species Y n and EX is a step operator defined as for any function f(·). The corresponding RRE describing the deterministic time evolution of the concentrations xn = Xn /Ω and yn = Yn /Ω is given in Eq. 6 (see Methods section).

For simplicity, we set k2 = k4 = 1. We also enforce the concentration x0 of the buffer X0 to be 1 at all times. Under these conditions, the fixed point of the deterministic RRE (Eq. 6) is given by xn (t → ∞) = k1 and yn (t → ∞) = k3/k1 for all n ≥ 1. This fixed point is exponentially stable if , undergoes a Hopf bifurcation at and becomes unstable for . In the latter case, xn (t) and yn (t) exhibit oscillations for each n = 1,…,N. In the deterministic RRE description, the condition for a limit cycle has to be strictly fulfilled in order to observe oscillatory behavior, whereas in the stochastic description oscillations can be observed even when the limit-cycle condition is not fulfilled27,5.

We numerically sample trajectories from the CME (Eq. 2) using the direct method46, an exact formulation of Gillespie's stochastic simulation algorithm36, for different reactor volumes Ω. The reactor volume determines the magnitude of intrinsic noise, as smaller Ω decrease the total number of reactive molecules in the system and hence increase the intrinsic noise magnitude. We set N = 20, thus simulating a cascade of 20 Brusselator stages, which includes the single-stage case when looking at the concentrations in stage 1, since they are independent of any subsequent stages. This value for N is chosen arbitrarily and the results would not change if a different N were chosen. The concentrations of all species are 0 at time t = 0. We also set k1 = 1 and k3 = 1. For these parameters, the fixed point of the system is stable and the deterministic system does hence not exhibit limit-cycle oscillations, reaching the fixed point (xn , yn ) = (1,1) for all n = 1,…,N. The mesoscopic system, however, shows oscillations due to the concentration fluctuations from intrinsic noise. This can be seen in Fig. 2, where the deterministic RRE trajectories from the first and last cascade stages are shown in panels (b) and (d), respectively and a single trajectory sampled from the CME in panels (a) and (c). Starting from the above initial condition, the stochastic trajectory shows sustained oscillations, whereas the deterministic trajectory reaches the stable fixed point.

Figure 2
figure 2

Plot of a single trajectory in phase space (xn , yn) for the first and last stages, n = 1 and n = 20, of the model system (Eq.

1) with N = 20 and reactor volume Ω = 100. For this system, the RRE predict an exponentially stable fixed point at (xn , yn ) = (1, 1). (a) A single stochastic trajectory sampled from the CME for stage n = 1; (b) the corresponding deterministic RRE prediction for the same parameters. (c, d) Stochastic and deterministic trajectories, respectively, for the last stage of the cascade.

Full size image

We study the normalized steady-state PSD Sn (ω) of the concentration fluctuations of species X n (species X of the n-th stage) for n = 1,…,N as a function of the angular frequency ω for different reactor volumes Ω. The normalized steady-state PSD Sn (ω) is defined as the Fourier transform of the time-autocorrelation function Cn (τ):

where the time autocorrelation in function of the time lag τ is given by

The subscript s denotes quantities computed at steady state, and the variance at steady state . The normalization of Cn (τ) with factors out the energy of the fluctuations, so that . We hence call Sn (ω) the normalized steady-state PSD. It quantifies the fraction of energy of the fluctuations around a specific frequency, namely, Sn (ω)dω gives the fraction of energy of the fluctuations between ω and ω + dω. We compute Sn (ω) by recording a single long trajectory of xn (t) at steady state. We sample 8 404 992 (223 + 214) data points of xn (t) starting from t = 2000 with a time resolution of δt = 0.1. We then compute the time-autocorrelation function (Eq. 4) from a minimum lag of τ = 0.1 up to a maximum lag of τ = 214δt. Sn (ω) is obtained by fast Fourier transform (Eq. 3).

We quantify the effect of intrinsic noise by the PSD's peak frequency and bandwidth. The peak frequency is defined as the angular frequency at which Sn (ω) is maximum, hence

Since Sn(ω) is generated by a stochastic process and hence is noisy, we smooth Sn (ω) before computing . Smoothing is done using a moving-average filter with a window diameter of 10 data points, corresponding to a frequency-space resolution of δω = 2 · 10−2 (data points in frequency space are uniformly spaced with a distance of 2 · 10−3).

The bandwidth of the steady-state PSD is defined as the difference between the two frequencies (ω 1, ω 2) where the steady-state PSD drops to half of its maximum value, i.e., so that with ω 2 > ω 1. Also is computed on the smoothed PSD.

In the linear-noise (large volume) regime, the quantities Sn (ω) and can be calculated analytically38,15 (see Methods section). We use the results from the linear-noise regime as a baseline to understand the effect of intrinsic noise on our model system.

Effect of noise

We present the normalized steady-state PSD Sn (ω), the peak frequency and the bandwidth for different reactor volumes Ω of our model system. These quantities are numerically computed from exact SSA trajectories46,35 as described above. In the linear-noise limit, the quantities are analytically computed as described in the Methods section.

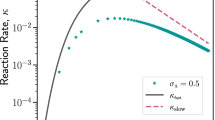
First, we assess Sn (ω) as a function of reactor volume Ω for the stage n = 1 alone and then extend our results to cascades of coupled Brusselators. Figure 3(a) shows S1(ω) for three different reactor volumes Ω = 1, 5, 50 and in the linear-noise limit. It can be seen that the steady-state PSD is indeed a function of Ω and that it has a Lorentzian-like form with a peak frequency and an associated bandwidth. This form of the steady-state PSD is expected, since the time-autocorrelation function is . As the volume Ω is reduced, the peak shifts to lower frequencies. The linear-noise regime is the weak-noise limit for large Ω. For Ω = 50 the peak frequency is . This reduces to and for Ω = 5 and Ω = 1, respectively.

Figure 3
figure 3

Effect of intrinsic noise on the frequency spectrum of non-equilibrium steady-state concentration fluctuations.

(a) Normalized steady-state power spectral density S1(ω) of the fluctuations of species X1 (see Eq. 3) for a single Brusselator in different reactor volumes Ω = 1, 5, 50 and in the linear-noise limit for large, macroscopic Ω (see Methods section), the latter reflecting the baseline. (b) Normalized steady-state power spectral density S20(ω) of the fluctuations of species X20 at the last stage of a cascade of 20 downstream-coupled Brusselators in different reactor volumes Ω = 1, 5, 50 and in the linear-noise limit for large Ω.

Full size image

The bandwidth for Ω = 50 is . For Ω = 5, it increases to and for Ω = 1 further to . The bandwidth of the steady-state PSD hence increases with decreasing reactor volume Ω.

We now consider how these results change along a cascade of downstream-coupled Brusselators. Figure 3(b) shows S20(ω) at stage n = 20 for the same three reactor volumes Ω = 1, 5, 50 and in the linear-noise limit. Similar to what is observed in the first stage, the peak also shifts toward lower frequencies as Ω decreases. For Ω = 50 the peak frequency is , which reduces to and for Ω = 5 and Ω = 1, respectively. For a given Ω, the peak frequency is successively reduced by each cascase stage, hence .

The bandwidth at stage n = 20 also increases with decreasing volume, just as it did for the first stage (see Fig. 3(b)). For Ω = 50, 5 and 1, we find , and , respectively. Comparing and , we observe that for fixed reactor volume Ω the bandwidth decreases with every stage along the cascade.

These results are summarized in Table 1 and shown also for intermediate cascade stages in Fig. 4. We observe that for a given cascade stage n the peak frequency decreases with decreasing reactor volume and that for a given reactor volume the peak frequency also decreases with every stage along the cascade. In the linearized approximation (valid for large volumes), the peak frequency is independent of the reactor volume and also of the cascade stage (see Eq. 14). This indicates that the effects observed for smaller volumes are indeed caused by intrinsic noise in the system.

Table 1 The effect of intrinsic noise, realized by decreasing the reactor volume Ω, on the peak frequency (see Eq. 5) and the bandwidth of the normalized steady-state PSD Sn () (see Eq. 3) for stages n = 1 and n = 20 of a cascade of downstream-coupled Brusselators (see Eq. 1).
Full size table
Figure 4
figure 4

Peak frequency of the normalized steady-state power spectral density Sn (ω) as a function of cascade stage n in different reactor volumes Ω.

The results for “large Ω” are obtained from the analytical expressions in the linear-noise limit (see Methods section).

Full size image

Discussion

We have studied the effect of intrinsic noise due to molecular discreteness on mesoscopic oscillatory chemical reaction networks. We considered the model system of a Brusselator away from the Hopf bifurcation, where the deterministic reaction rate equations (RRE) do not exhibit oscillatory behavior. Oscillations can nevertheless be induced by intrinsic noise, the magnitude of which was tuned by changing the reactor volume. We also studied propagation of noise-induced effects along a downstream-coupled cascade of Brusselators. Noise-induced effects were quantified using the frequency spectrum of concentration fluctuations, given by the normalized power spectral density (PSD), at a non-equilibrium steady state. Specifically, we used the peak frequency and the bandwidth of the PSD as fingerprints of noise-induced effects. We used an exact stochastic simulation algorithm46,35 to study the kinetics of the system as governed by the corresponding chemical master equation.

The results have shown that the frequency at which the steady-state PSD is maximal decreases with decreasing reactor volume. This effect is further amplified by every stage of a cascade of coupled Brusselators, leading to a further decrease along the cascade. This is in contrast to the linearized approximation, which does not predict any effect of intrinsic noise on the normalized steady-state PSD. We also showed that for a given cascade stage the bandwidth of concentration fluctuations decreases with increasing reactor volume, which is in agreement with observations in non-oscillatory monostable22 and oscillatory34,30 chemical reaction systems. For a fixed volume, the bandwidth also decreases along the cascade, rendering the peak sharper and more pronounced with every stage. One may hence speculate whether intrinsic noise plays any role in “tuning” the output frequency of biochemical oscillators. This tuned output frequency could in turn drive further downstream reaction networks, qualitatively changing their behavior. It is for example known that the behavior of glycolytic oscillators can change from periodic to quasi-periodic to chaotic upon small changes in the driving input frequency (see p. 33, Fig. 2.24, in Ref.47, or Refs.48,49).

We believe that our study sheds light on the role of intrinsic noise in chemical oscillators. Even though we studied a simple model system, the results show how intrinsic noise qualitatively influences the frequency spectrum of the oscillations. We have shown that mesoscopic chemical reaction networks and cascades thereof, exhibit different output spectra depending on the magnitude of intrinsic noise. We expect this effect to be present also in mesoscopic oscillatory reaction systems where the RRE show oscillatory behavior. This is because there is no qualitative difference in the concentration trajectories of mesoscopic systems just before and after a Hopf bifurcation27.

Our findings are relevant for identifying the reactor volumes of (cascades of) mesoscopic reaction networks when the concentration fluctuations are measured experimentally, e.g., using fluorescence correction spectroscopy. In addition, we believe that the effects reported here can be used as fingerprints to more reliably identify parameters of stochastic chemical reaction networks in systems biology models. Finally, the results presented here might contribute towards developing a general understanding of how noise influences the kinetics of different chemical systems, when deterministic RRE predictions are valid and what deviations are to be expected otherwise.

Methods

Flutuations around the linearized RRE

We analytically derive the normalized steady-state PSD Sn (ω) and its peak frequency for each cascade stage n in the linear-noise regime. The derivation follows that of Shibata [5] and is valid in the weak-noise limit at large (macroscopic) volumes Ω.

The deterministic RRE for the reaction system given in Eq. 1 are

where xn and yn are the concentrations of species X n and Y n , respectively. As in the numerical study for mesoscopic volumes, we set k2 = k4 = x0 = 1. Let δxn and δyn be small perturbations around the steady state (xn , yn ) = (k1, k3/k1). The linear equations for the perturbations around the steady state are given by

This expression for the perturbations around the fixed point of the RRE is the same as the one that can be obtained from the linear-noise approximation using van-Kampen expansion.

Taking the Fourier transform on both sides, we obtain

where and are the Fourier transforms of xn (t) and yn (t), respectively. Simplifying the above equation leads to

where

Since we consider a linearized version of the macroscopic system, the normalized PSD is invariant to the input noise excitation used to quantify the correlations introduced by the system. We here use the simple input noise δx0 = ε 0(t), which is uncorrelated white noise with 〈ε 0(t)〉 = 0 and , where δ(τ) is the Dirac delta distribution. The PSD P0(ω) of the input buffer to the first stage is then given by

The PSD Pn (ω) of the output of cascade stage n ≥ 1 is given by

Substituting Eqs. 9 and 11 into Eq. 12 we get

The normalized steady-state PSD Sn (ω) is then

Given the expression for F(ω) (Eq. 10), the normalized steady-state PSD Sn (ω) has a Lorentzian-like form with peak frequency

It is therefore evident that in the linear-noise regime the peak frequency is independent of Ω and of the stage number n. The bandwidth in the linear-noise limit is computed directly from Eq. 13.