Main

Owing to its hexagonal lattice structure with a diatomic unit cell, graphene has low-energy electronic properties that are governed by the massless Dirac equation6. This has a number of consequences, among them Klein tunnelling7,8,9,10, which prevents electrostatic confinement of charge carriers and inhibits the fabrication of standard semiconductor devices. This has motivated a number of recent theoretical investigations of graphene in periodic potentials2,3,11,12,13,14,15, which explored ways of controlling the propagation of charge carriers by means of various superlattice potentials. On the analytical side, one-dimensional potentials render particle propagation anisotropic2,3,11,14 and generate new Dirac points, where the electron and hole bands meet, at energies ±ℏvF|G|/2 given by the reciprocal superlattice vectors G(refs 2, 3), where vF is the Fermi velocity. Numerical approaches have extended several of these results to the case of two-dimensional potentials2,3,14,15. Unlike for Schrödinger fermions, the periodic potentials generally induce new Dirac points but do not open bandgaps in graphene, owing to the chiral nature of the Dirac fermions.

Recent scanning tunnelling microscope (STM) topography experiments have reported well-developed moiré patterns in graphene on crystalline substrates, which suggests that the latter generate effective periodic potentials4,5,16,17. Of particular interest is hexagonal boron nitride (hBN), because it is an insulator which only couples weakly to graphene. Furthermore, graphene on hBN exhibits the highest mobility ever reported for graphene on any substrate18, and has strongly suppressed charge inhomogeneities4,5. Hexagonal boron nitride is a layered material whose planes have the same atomic structure as graphene, with a 1.8% longer lattice constant. The influence of the weak graphene–substrate interlayer coupling on the electronic transport and spectroscopic properties of graphene is not well understood. In particular, there is to date no theory for local electronic properties such as those probed in STM experiments. Below, we show that periodic interlayer couplings generate new Dirac points at an energy determined by the wave vector of the periodic potential. The presence of these new Dirac points is reflected in two dips in the density of states, symmetrically placed at E=±ℏvF|G|/2 around the E=0 graphene Dirac point but generally of asymmetric strength. There is also a periodic modulation of the local density of states with the same period as the superlattice topographic moiré pattern.

The fabrication procedure used for creating the graphene on hBN devices results in a random rotational orientation between the graphene and hBN lattices. This rotation between the lattices and the longer lattice constant for hBN leads to topographic moiré patterns. Given the lattice mismatch δ between hBN and graphene, the relative rotation angle φ between the two lattices uniquely determines the moiré wavelength λ as

where a is the graphene lattice constant. The relative rotation angle θ of the moiré pattern with respect to the graphene lattice is given by

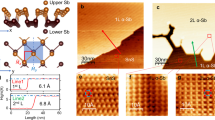
Figure 1b plots the wavelength of the moiré pattern (black) and rotation angle (red) as a function of φ. Owing to the lattice mismatch, there is a moiré pattern for all orientations of graphene on hBN with a maximum possible length of about 14 nm. Figure 1c–e shows STM topography images of moiré patterns for three different rotations of the graphene lattice.

Figure 1: Graphene device schematic and STM moiré images.
figure 1

a, Schematic of the measurement set-up showing the STM tip and an optical microscope image of one of the measured samples. b, Superlattice wavelength (black) and rotation (red) as a function of the angle between the graphene and hBN lattices. c–e, STM topography images showing 2.4 nm (c), 6.0 nm (d) and 11.5 nm (e) moiré patterns. Typical imaging parameters were sample voltages between 0.3 V and 0.5 V and tunnel currents between 100 pA and 150 pA. The scale bars in all images are 5 nm.

Full size image

We explore how this moiré structure influences the local density of states (LDOS) in the graphene layer. This quantity dominates dI/dV STM measurements as long as the density of states of the STM tip and the tunnelling rate from the tip to the sample are constant. We take a lattice Hamiltonian for a graphene monolayer deposited on top of a hBN monolayer, where the two layers are rotated with respect to one another, and the spatially dependent interlayer hopping is calculated from nearest-neighbour and next-nearest-neighbour interlayer coupling4. We numerically calculate ρ(r,E) for this model using the Lanczos method19 (see Supplementary Information).

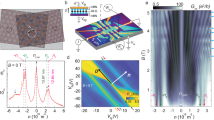
Dips in the calculated ρ(r,E) are clearly seen in Fig. 2a. The energy of these dips changes as a function of the rotation angle φ and hence the moiré wavelength. We have also observed the dips in the experimental dI/dV curves as shown in Fig. 2b. The black curve is for a 9.0 nm moiré pattern and the energy of the dip is 0.28 eV from the Dirac point. The red curve is for a 13.4 nm moiré pattern and the energy of the dips decreases to 0.22 eV from the Dirac point. Both experimentally and theoretically, we found that the relative strength of the dips in the conduction and valence band are different, with the dip in the valence band being much deeper than the dip in the conduction band. In our numerical calculations, we identified that most of this asymmetry arises because of next-nearest-neighbour interlayer coupling, which effectively induces modulated hopping between different graphene sublattices and breaks electron–hole symmetry (see Supplementary Information). Figure 2c plots |d2I/dV2| for the 9.0 nm moiré pattern as a function of gate voltage and sample voltage. We clearly see the Dirac point in this measurement crossing the Fermi energy near zero gate voltage. There is a second dip which moves parallel to it that is offset by −0.28 V in sample voltage. This dip is due to the superlattice periodic potential induced by the hBN and indicates the emergence of new superlattice Dirac points.

Figure 2: Density of states of graphene on hBN showing new superlattice Dirac points.
figure 2

a, Theoretical LDOS curves for three different rotation angles between graphene and hBN, red is φ=0.5° (12.5 nm), blue is φ=1° (10.0 nm) and green is φ=2° (6.3 nm). The curves have been vertically offset for clarity. b, Experimental dI/dV curves for two different moiré wavelengths, 9.0 nm (black) and 13.4 nm (red). The dips in the dI/dV curves are marked by arrows. c, |d2I/dV2| as a function of gate and sample voltage for the 9.0 nm moiré pattern, showing the shift of the Dirac point and one of the dips. d, Energy of the dips away from the Dirac point as a function of moiré wavelength. The red points are the experimentally measured values and the black line is the expected theoretical dependence. The error bars in energy represent the minimum and maximum observed energies. The error bars in wavelength represent the standard deviation.

Full size image

We have observed these dips in the LDOS for seven different moiré wavelengths. The energy of the dips from the Dirac point is plotted (red points) as a function of wavelength in Fig. 2d. The solid black line plots the expected energy dependence , assuming the linear band structure of graphene and vF=1.1×106 m s−1. For the necessary high-resolution spectroscopy, our STM is limited to observing dips in an energy range of ∼ ±1 V, which restricts the moiré wavelengths to longer than 2 nm. At higher energies, the spectroscopy tends to be smoothed by interaction effects which modify the lifetime of the graphene quasiparticles20, making the identification of dips difficult.

To better understand these dips, we focus on the low-energy regime and neglect intervalley scattering in graphene. This is justified by the energy range in our STM experiments and the long wavelength of the moiré potential. The interlayer hopping term between the graphene and hBN layers reflects the same periodic structure as the moiré pattern4. Therefore we model the influence of the hBN by an effective periodic potential with the same symmetry as the observed moiré pattern. We accordingly consider the single-valley Hamiltonian

where k=(kx,ky), is a vector of Pauli matrices and is the identity matrix. The potential strength is estimated as V =0.06 eV from numerical second-order perturbation theory, and the Gα are the reciprocal superlattice vectors corresponding to the periodic potential generated by the hBN substrate. The reciprocal superlattice vector is determined by the relative rotation of the graphene and hBN lattices according to equations (1) and (2). The other superlattice wave vectors are obtained by two rotations of 60°. Larger superlattice vectors are not included in our model, because the corresponding couplings are smaller by more than one order of magnitude4.

The dips in ρ(r,E) are due to k→−k processes induced by the periodic potential for values 2k=Gα corresponding to one of the reciprocal superlattice vectors Gα. Unlike for Schrödinger particles, the chirality of the Dirac fermions prevents such processes from opening a bandgap at the edges of the superlattice Brillouin zone, as long as the potential does not break sublattice symmetry (see Supplementary Information).

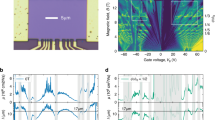
The presence of the new superlattice Dirac points can be detected by examining the gate dependence of the LDOS. As seen in Fig. 2c, the two Dirac points move in parallel with the gate voltage. Figure 3a plots dI/dV for a 13.4 nm moiré pattern over a larger range of gate voltage than in Fig. 2c. The white dashed lines show the energy of the two Dirac points as a function of gate voltage. When the Fermi energy approaches the superlattice Dirac point, the gate dependence of the Dirac points changes. This is plotted in Fig. 3b, which tracks the energy of the original Dirac point when the Fermi energy crosses the superlattice Dirac point at −53 V. Both Dirac points move more quickly with gate voltage, indicating a reduced density of states at this energy. The gate dependence for the original Dirac point is given by the equation

where V g is the gate voltage, V 0 is the offset voltage, α is the coupling to the gate and gv is the valley degeneracy. When the Fermi energy is near the original Dirac point, the valley degeneracy is gv=2 and from the fit we extract the value of the Fermi velocity at the original Dirac point to be vF=vF0=0.94±0.02×106 m s−1 for both electrons and holes. At the new superlattice Dirac points, the valley degeneracy is gv=6 because the periodic potential creates three superlattice Dirac points in each of the original Dirac cones corresponding to the three reciprocal lattice vectors Gα. Furthermore, the Dirac cones are anisotropic and therefore the constant energy contours are given by ellipses rather than circles. Therefore, the Fermi velocity in equation (3) must be modified to where vF0 is the unmodified Fermi velocity parallel to Gα and vF* is the reduced Fermi velocity perpendicular to Gα. From the fit near the energy of the superlattice Dirac points, we find that vF*=0.5±0.1×106 m s−1 for the new electrons and holes. The reduction is in qualitative agreement with our numerical calculations in the Supplementary Information. Evidence for the presence of the superlattice Dirac points can also be seen in the global conductivity as a function of gate voltage (see Supplementary Information).

Figure 3: Gate dependence of graphene density of states near the superlattice Dirac points for a 13.4 nm moiré pattern.
figure 3

a, dI/dV as a function of sample and gate voltage showing both the Dirac point and the new superlattice Dirac point. The white dashed lines mark the locations of the Dirac point and the superlattice Dirac point. b, Shift of the Dirac point as a function of gate voltage when the superlattice Dirac point crosses the Fermi energy (black line). The solid red line is a theoretical fit for the shift of the Dirac point with the presence of the superlattice Dirac points. The dashed red line shows the expected shift without the superlattice Dirac points. The inset shows the shift of both Dirac points over a large gate voltage range as well as theoretical fits (red and blue solid lines).

Full size image

As well as the formation of superlattice Dirac points, the presence of the periodic potential also leads to a spatial variation in the LDOS. Figure 4 shows experimental and numerical images of the LDOS as a function of energy. Near the Dirac point, (Fig. 4b,e), we observe a nearly featureless density of states. This is in agreement with previous STM measurements which show a strong suppression of charge fluctuations in graphene on hBN (refs 4, 5). At higher energies, the presence of the moiré potential manifests itself as a local variation in the density of states. Figure 4a and d are taken at a lower energy than the superlattice Dirac points in the valence band. At this energy the hexagonal pattern of the potential is clearly visible. On the conduction band side, Figs. 4c and f, the moiré pattern is once again visible but its contrast is inverted. The centres of the hexagons now correspond to points of increased density of states. However, the dips in the LDOS from the superlattice Dirac points occur at the same energy independent of the location on the superlattice. We observe that the moiré pattern becomes much more visible in the local density of states at energies above the superlattice Dirac points. Previous measurements of the LDOS in graphene on hBN did not observe any variations due to the short moiré patterns and low energies probed4.

Figure 4: Experimental and theoretical images of LDOS for a long wavelength moiré pattern.
figure 4

a–c, Experimental dI/dV maps for a 13.4 nm moiré pattern. The sample voltages are −0.16 V (a), 0.17 V (b) and 0.44 V (c). The sample voltage in b is near the Dirac point because the gate voltage was 60 V whereas the other two maps are near the energy of the superlattice Dirac points. d–f, Theoretical dI/dV maps for a 13.4 nm moiré pattern. The energies are −0.3 eV (d), 0.03 eV (e) and 0.3 eV (f). The energy in e corresponds to the Dirac point and is shifted from the experimental images because of the gate voltage. The scale bars in all images are 10 nm.

Full size image

Graphene-on-hBN devices are becoming widely used owing to their improved mobility and reduced charged impurities. We have shown that lattice mismatch and relative rotation between the graphene and hBN leads to a periodic potential for graphene charge carriers. This potential creates new Dirac points whose energy is determined by the wavelength of the potential. These superlattice Dirac points have the potential to control the transport properties of electrons in graphene as it induces anisotropic velocities for the charge carriers. Future work is necessary to exploit this periodic potential for the creation of novel graphene devices.

Methods

Graphene on hBN devices were fabricated using two different methods. In the first method, mechanically exfoliated graphene was transferred to high-quality single crystals of hBN which were mechanically exfoliated on a SiO2 substrate4,18. In the second method, commercially available hBN (Momentive AC6004) was exfoliated on SiO2 substrates and then CVD grown graphene was deposited over the hBN. Both types of devices gave similar results, so we do not distinguish between the two types. After depositing the graphene on hBN, Cr/Au electrodes were written using electron beam lithography. The devices were annealed at 350 °C for 2 h in a mixture of argon and hydrogen and then at 300 °C for 1 h in air before being transferred to the ultrahigh vacuum low-temperature STM for topographic and spectroscopic measurements. We have measured a total of 29 samples of which seven had long enough moiré patterns for the observation of a superlattice Dirac point.

Figure 1a shows a schematic diagram of the measurement set-up used for imaging and spectroscopy of the graphene flakes. All the measurements were performed in ultrahigh vacuum at a temperature of 4.5 K. dI/dV measurements were acquired by turning off the feedback circuit and adding a small (5–10 mV) a.c. voltage at 563 Hz to the sample voltage. The current was measured by lock-in detection.