Main

The study of many-body quantum entangled states including atomic spin squeezed states is an active research frontier. In addition to being intrinsically fascinating, such states have applications in precision measurements, quantum information and fundamental tests of quantum mechanics4. Squeezed states were first demonstrated in optical fields5 and later with ensembles of pseudo-spin-1/2 atoms using nonlinear atom–light interactions6. For spin-1/2 particles, coherent states of the system are uniquely specified by the components of the total spin vector 〈S〉, typically illustrated on an SU(2) Bloch sphere. For particles with higher spin, further degrees of freedom beyond the spin vector are required to fully specify the state. For spin-1 particles, a natural basis to describe the wavefunction is the SU(3) Cartesian dipole–quadrupole basis, consisting of the three components of the spin vector, , and the moments of the rank-2 quadrupole or nematic tensor, ({i,j}∈{x,y,z}). In matrix form, the nematic moments can be written Qi j=SiSj+SjSi−(4/3)δi j, where δi j is the Kronecker delta.

Spin-1 atomic Bose–Einstein condensates7,8,9,10,11 provide an exceptionally clean experimental platform to investigate the quantum dynamics of many-body spin systems and have been realized using the f=1 hyperfine manifold of 87Rb and 23Na. They feature controllable quantum phase transitions, well-understood underlying microscopic models and flexible defect-free geometries. Importantly, it is possible to initialize non-equilibrium or excited states of the system and to directly measure both the spin vector and the nematic tensor using standard atomic-state manipulation tools. It was demonstrated in ref. 12 that the spinor interaction can be written as total spin angular momentum, , where . It is natural to describe this many-body system in the second quantized formalism in terms of the mode operators of three Zeeman states (for example ). Here ai are particle annihilation operators for the magnetic sublevels mf=−1,0,1, and we use the single-mode approximation where the modes share the same spatial wavefunction ϕ(r) determined by the spin-independent part of the Hamiltonian. The spinor Hamiltonian describing the collisionally induced spin dynamics of the condensate and the effects of an applied magnetic field B (by convention along the z axis) can be written (Supplementary Information)

Here λ and q∝B2 characterize the inter-spin and Zeeman energies, respectively, and . At high fields, the system favours nematic ordering of the spins, an eigenstate of . This is a state with 〈S〉=0 with broken rotational symmetry given by the anisotropy of spin fluctuations, for example , and whose alignment is specified by a time-reversal invariant ‘director’, in this case the z axis. In the Fock basis, |N1,N0,N−1〉, this is just the state with all N atoms in the mf=0 state: |0,N,0〉. At low fields, the sign of λ determines whether the interactions favour a ferromagnetic (λ<0, that is 87Rb used in our work) or anti-ferromagnetic (λ>0, that is 23Na) ground state, with the ground states being maximum and minimum total spin respectively. At intermediate fields, the system undergoes a quantum phase transition between orders with a quantum critical point at q=2|c|for the ferromagnetic case, where c=2N λ (ref. 13).

In spin-1/2 systems, nonlinear Hamiltonians such as Sz2 produce squeezing of the spin variables satisfying Heisenberg uncertainty relations, for example ΔSxΔSy≥(1/2)|〈Sz〉|. Although criteria for squeezing and entanglement are now well established for spin-1/2 particles within an SU(2) framework, there was considerable early discussion about different squeezing definitions14,15. There has been much less work for higher-spin particles with correspondingly higher symmetries. Squeezing in spin-1 systems has been studied from the perspective of two-mode squeezing16,17,18,19, in terms of the Gell-Mann (quark) framework of the SU(3) algebra20 and in terms of spin-nematic measurables21. Very recently, general criteria for spin squeezing for arbitrary spin particles have been developed22.

The source of squeezing in a spin-1 condensate is the nonlinear collisional spin interaction , which reduces to for states with of interest here. This Hamiltonian contains four-wave mixing terms, , which generate squeezing that can be described using a two-mode formalism where the modes are the signal and idler (Supplementary Information). Here we prefer an analysis using the commutators of the SU(3) group describing the spin-1 system, as it provides more insight. Experimental investigations of spin-1 condensates have been predominantly in the mean-field limit; however, first explorations beyond the mean field have been reported23,24,25,26.

From the generalized uncertainty relation , only operator pairs with non-zero expectation values for their commutation relations can exhibit squeezing. For condensates with the atoms in the mf=0 state, only two of the SU(3) commutators have non-zero expectation values: and , leading to the relevant uncertainty relations ΔSxΔQy z≥N and ΔSyΔQx z≥N. For each of these, the uncertainty relationship is between a spin operator and a quadrupole nematic operator; these operators and their commutators define two subspaces. From these relations, two squeezing parameters are defined in terms of quadratures of the operators:

with θ as the quadrature angle18,21. Squeezing within a given SU(2) subspace is indicated by the variance of the quadrature operator being less than the standard quantum limit of N for some value of θ.

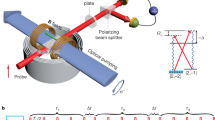
The experimental sequence is illustrated in Fig. 1 with the help of the spin SU(2) subspace {Sx,Sy,Sz} and both of the subspaces that exhibit squeezing, {Sx,Qy z,Qz z} and {Sy,Qx z,Qz z} (Supplementary Information). The initial state of the condensate is shown in Fig. 1a. It has no spin moment, 〈S〉=0, but non-zero diagonal quadrupole elements , and uncorrelated equal uncertainties in Sx,Sy,Qx z,Qy z. Subsequent evolution is governed by equation (1) in the regime q≤2|c|. Out-of-equilibrium dynamics of spin-1 condensates generally exhibit oscillatory behaviour in the spin components27,28, except near a separatrix (green contour) in phase space where the period diverges29. For our case, the initial state lies on the separatrix, and hence evolution is wholly dictated by quantum fluctuations corresponding to the initial uncertainties. These uncertainties evolve exponentially, generating anti-squeezing for a quadrature of {Sx,Qy z} aligned along a branch of the separatrix and squeezing for the orthogonal quadrature, as shown in Fig 1b. Measuring the squeezing requires state tomography involving two SU(3) rotations. The first is a rotation about Qz z that rotates the quadrature squeezing to align to Sx. Conceptually, Qz z is the generator of the rotation in the squeezed subspaces and the rotation of the quadrature angle is given by the operator exp(iΔθ Qz z). The second is a π/2 rotation about the Sy axis (in the laboratory frame) that rotates the fluctuations in Sxinto the measurement basis, Sz=N1−N−1 (Fig. 1d). These manipulations are equivalent to the homodyne technique used in quantum optics to measure two-mode squeezing where the mode is the local oscillator (Supplementary Information).

Figure 1: Illustration of the experimental sequence using semi-classical simulation and quasi-probability distributions.
figure 1

a, The initial state is a condensate with the atoms prepared in the mf=0 state. An N=30-atom distribution is used to emphasize features. b, After 25 ms of evolution, spin-nematic squeezing develops along the separatrix (green line) in the upper two spheres. c, A microwave pulse rotates the quadrature phase. For comparison the state from the previous plot is shown in red in the upper two spheres. d, A π/2 radiofrequency pulse rotates the transverse magnetization Sx into Sz. For comparison the state from the previous plot is shown in red in the lower two spheres. e, After the trap is turned off, a Stern–Gerlach field is applied during the time-of-flight expansion and the clouds of atoms are counted using fluorescence imaging. Measurements of 〈Sz〉=N1−N−1 are shown for 100 runs of a squeezed quadrature (green) and an unsqueezed quadrature (orange).

Full size image

Identical squeezing also occurs in the degenerate {Sy,Qx z,Qz z} subspace, which leads to an important, but subtle, point. In the laboratory frame, the system does not confine itself to either of the SU(2) subspaces but rather undergoes rapid Larmor precession described by rotations about Szin two other SU(2) subspaces, {Sx,Sy,Sz} and {Qy z,Qx z,Sz} (not shown). However, because the squeezing is identical in both subspaces, and the Larmor precession of the spin vector and quadrupole are synchronized, it is not necessary to track the precession to measure squeezing. This has important experimental consequences in that it is not necessary to maintain synchronization with the Larmor rotation to carry out quantum state tomography.

For the experiment, we prepare a condensate of N=45,000, 87Rb atoms in the |f=1,mf=0〉 hyperfine state in a high magnetic field (2 G). The condensate is tightly confined in an optical dipole trap with trap frequencies of 250 Hz. For these parameters, the Thomas–Fermi radii of the condensate are 3.8 μmand the spin healing length is 11 μm, indicating that the condensate is well described by the single-mode approximation. To initiate evolution, the condensate is quenched below the quantum critical point by lowering the magnetic field to a value of 210 mG and then allowed to freely evolve for a set time. During this evolution the squeezing is developed. Note that during this time there is essentially no population transfer (<1%) from the mf=0 state (Fig. 2c top), hence this corresponds to squeezed vacuum of the mf=±1 modes. The quadrature rotation is accomplished by shifting the phase of the mf=0 amplitude using a microwave detuned from the clock transition. This is immediately followed by an RF rotation to rotate Sx into Sz. The trap is then turned off and a Stern–Gerlach field is applied to separate the mf components during a 22 ms time-of-flight expansion. The atoms are probed for 400 μs with three pairs of orthogonal laser beams, and the resulting fluorescence signal is collected by a CCD (charge-coupled device) camera. Sample Sz measurements are shown in Fig. 1e for two different quadrature angles and show qualitatively both enhanced and suppressed fluctuations.

Figure 2: Comparison of measured quadrature fluctuations with a fully quantum calculation.
figure 2

a, Measurement of the quadrature variances for different evolution times and quadrature phase shifts. The phase shift is calculated from the microwave detuning normalized to the on-resonance Rabi rate (Supplementary Information). b, Detailed view of the maximum squeezing for different evolution times. The phase of data is shifted to match the simulation. c, Time evolution of the populations and the maximum and minimum quadrature variances. The squeezing measurement is made before significant population evolution. Estimated errors are approximately the size of the markers for both phase and variance. Open markers are statistics of the raw data; filled markers have been corrected for PSN, but the difference is negligible for all but the most squeezed data points.

Full size image

The experiment cycle is repeated 100 times for each quadrature angle to collect sufficient statistics to determine the fluctuations ξx2. The measurement results are shown in Fig. 2 for different evolution times. The fluctuations clearly exhibit noise reduced below the standard quantum limit (ξx2<0 dB) for certain quadrature phases and show increased noise π/2 radians away. The measurements are compared to a fully quantum theoretical calculation (Supplementary Information) carried out by numerically integrating equation (1) with a spinor dynamical rate c/h=−8 Hz (h is Planck’s constant) and q(t) determined experimentally using microwave spectroscopy. The spinor dynamical rate is chosen to match the degree of anti-squeezing observed and is also a good fit to the long-time evolution of the populations (Fig. 2c top) as well as estimates from the trap frequencies and N.

As evolution time is increased, the maximum variance shows anti-squeezing that increases in good agreement with the simulation (Fig. 2c. black lines) and is approximately exponential with a time constant of (2|c|/ℏ)−1 given by the two-mode squeezing model (Fig. 2c, red lines). The minimum variance shows squeezing that limits asymptotically after ∼ 30 ms of evolution owing to detection noise from a combination of light scattered by the apparatus and the photoelectron shot noise (PSN). The PSN limit is indicated by the grey lines in Fig. 2. The maximum observed squeezing is −8.3−0.7+0.6 dB, which is the highest degree of quadrature squeezing observed in any atomic system. When corrected for the PSN, it is possible to infer a ‘corrected’ squeezing parameter of −10.3−0.9+0.7 dB that would be obtained with detection improvements. The phase of maximum squeezing also evolves in time, converging to the phase of the separatrix given by cos 2θ = −q/c−1 with a small (∼ 150 mrad) discrepancy between the measured phase of maximum squeezing and the theoretical prediction. After this initial time of approximately exponential squeezing, the minimum squeezing parameter reaches a turning point due to pump depletion.

We also reconstruct the phase space distribution of the squeezing for each time (Fig. 3) using an inverse Radon transform (Supplementary Information). The theoretical squeezing ellipse is shown for comparison. Just as the theoretical prediction shows, the quadrature evolves in both aspect ratio and phase rotation; however, quantitative agreement is limited by the finite number of data sets. Furthermore, the minimum width of parts c and d is limited by the PSN.

Figure 3: Reconstructions of the phase space for different evolution times.
figure 3

a, 15 ms, b, 30 ms, c, 45 ms and d, 65 ms. The last two are at half the scale of the first. The black trace in each is the calculated uncertainty ellipse from the simulation.

Full size image

Very recently, two papers related to ours have appeared30,31. These experiments share a similar spin mixing mechanism to generate quantum correlations, though in their case it is in the f=2 hyperfine manifold. For both of these other experiments, the starting point is the observation of strong non-classical fluctuations of Sz = N1 − N−1 due to spin mixing, which we previously reported in ref. 26. In ref. 31, atomic homodyne detection of the quadrature fluctuations using a technique that is very similar to ours was demonstrated. In their case, they were not able to show that the fluctuations were smaller than the classical limit, only that the fluctuations were dependent on the local oscillator phase. Only by subtracting detection noise do they claim entanglement of the two modes at the 4±17 atom level. In ref. 30, the number-squeezed mf = ±1 states are coupled using a sequence of microwave transitions to realize a two-level pseudo-spin-1/2 system. On the corresponding Bloch sphere, the number-squeezed states are completely phase uncorrelated. By measuring the resulting variance and fourth moment of Sz, they were able to show that the angle could be determined with an uncertainty −1.6 dB below the classical limit. These other experiments are in the regime of twin-atom states where the mf = ±1 states are macroscopically populated, whereas in our case we are in the limit of negligible population of the two states corresponding to squeezing of the atomic vacuum modes.