Nonlinear detection of spin currents in graphene with non-magnetic electrodes

Abstract

The abilities to inject and detect spin carriers are fundamental for research on transport and manipulation of spin information^1,2. Pure electronic spin currents have been recently studied in nanoscale electronic devices using a non-local lateral geometry, both in metallic systems ³ and in semiconductors⁴. To unlock the full potential of spintronics we must understand the interactions of spin with other degrees of freedom. Such interactions have been explored recently, for example, by using spin Hall^5,6,7 or spin thermoelectric effects^6,8,9. Here we present the detection of non-local spin signals using non-magnetic detectors, through an as-yet-unexplored nonlinear interaction between spin and charge. In analogy to the Seebeck effect¹⁰, where a heat current generates a charge potential, we demonstrate that a spin current in a paramagnet leads to a charge potential, if the conductivity is energy dependent. We use graphene¹¹ as a model system to study this effect, as recently proposed¹². The physical concept demonstrated here is generally valid, opening new possibilities for spintronics.

Main

Previous reports on detection of spin signals using non-magnetic contacts have made use of spin–orbit interaction through the (inverse) spin Hall effect^5,6. Recently, large non-local signals in graphene have been attributed to an effect with similar phenomenology, given by the difference in Hall resistance between two (spin) channels induced by an applied perpendicular magnetic field⁷. Both effects produce a charge potential transversal to the direction of the spin current and are valid in the linear regime. In the present work we deal with a different concept based on a nonlinear interaction between spin and charge which results in charge potentials longitudinal to the spin current¹². This effect is solely based on the energy dependence of the conductivity σ(ε), not requiring spin–orbit interaction or external magnetic fields.

To explain the concept of detection of spin signals used here it is useful to make an analogy with thermoelectrics. As shown in Fig. 1a, a temperature gradient sets up a heat current. Under open-circuit conditions, this results in a built-up voltage V =−S(T₂−T₁), with S the Seebeck coefficient of the conducting system. For the case of diffusive spin transport¹³ (Fig. 1b) the electrochemical potential of each spin channel can be described as μ_±=μ_avg±Δμ, with Δμ the spin accumulation (created by electrical spin injection) in the conductor, which decays with a characteristic spin-relaxation length λ. The gradient in spin accumulation sets up a spin current, which results, for ferromagnetic or ferrimagnetic materials with a spin polarization of the conductivity¹³β, in a built-up voltage V =−(β/e)(Δμ₂−Δμ₁). While S is a general property of conductors, β is in general zero for paramagnetic materials. Therefore, pure spin currents are not expected to generate charge voltages in a paramagnet such as graphene. The latter is not true if we consider spin transport away from the Fermi level. When a sizable Δμ is present, each spin channel experiences a different conductivity even in a paramagnet, as long as the conductivity is energy dependent. So we consider a spin polarization of the conductivity induced by Δμ, which can be approximated as¹²β=−Δμ σ⁻¹∂ σ/∂ ε.

Figure 1: Analogy between spin and heat transport illustrated by electronic distributions f(ε).

a, A temperature gradient (T₂>T₁) sets up a heat current, with high-energy electrons moving towards the cold region and low-energy electrons moving towards the hot region. When the conductivity is energy dependent (here ∂ σ/∂ ε>0) a Seebeck voltage is built up under open-circuit conditions, to compensate for the different conductivities of high- and low-energy electrons. b, A gradient in spin accumulation Δμ sets up a spin current, with majority-spin electrons moving towards the region with lower Δμ and minority-spin electrons moving in the opposite direction. Similar to thermoelectricity, a voltage is built up if the conductivity is energy dependent owing to the different conductivities of the two electron spin species.

To complete the analogy, we define α=σ⁻¹∂ σ/∂ ε. The previous expressions for V are only valid when the coefficients S and β are independent of the driving forces T and Δμ, respectively. In reality, the Seebeck coefficient is given by the Mott formula^10,14S=−L₀e α T, with L₀=(π²/3)(k_B²/e²)the Lorentz number. In the limit T≈T₂−T₁, the Seebeck voltage depends quadratically on the driving force as V ∝L₀e α(T)². Similarly, for spin transport in a paramagnet, the induced spin polarization mentioned above (β=−αΔμ) also results in a quadratic dependence on the driving force as V ∝(α/e)(Δμ)². Owing to the common factor α the effect described here has similar behaviour to the Seebeck voltage, showing opposite polarity for electron and hole regimes. Furthermore, because Δμ is (to lowest order) linear in the injection current^3,15, the result is a second-order signal V ∝I².

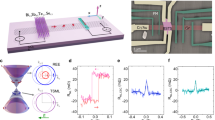
For our proof of concept we use graphene, which, apart from being a two-dimensional platform for relativistic quantum mechanics¹¹, has proved to be an excellent system for spin transport, where large values of Δμ≈1 meV can be obtained¹⁵. The sample is shown in Fig. 2a. It consists of a lateral graphene field-effect transistor covered with a thin aluminium oxide barrier that yields high-resistance contacts for efficient spin transport¹⁶ and electrostatic gating through the Si/SiO₂ substrate, as previously reported^15,17. As well as using magnetic Co contacts for electrical spin injection and detection (Fig. 2b), we also include Ti/Au contacts. These non-magnetic contacts are used to electrically detect spins in the configuration shown in Fig. 2c. There are two key aspects to such a measurement configuration. First, the use of non-magnetic detectors simplifies the analysis of the non-local signal, because for the case of using magnetic detectors both linear and nonlinear signals are expected owing to direct detection of Δμ (refs 12, 18). Second, the use of two magnetic contacts as source and drain for charge current enables us to measure the non-local signal for both parallel V ^Pa and antiparallel V ^Ap alignment of their magnetizations and thereby to focus on the difference between the two states ΔV. This way we can exclude background signals that do not depend on Δμ and can be present in non-local measurements¹⁸. We use a lock-in technique to determine the linear V₁ and second-order V₂ components of the resulting root-mean-square signal. From them we extract the non-local resistances R_icontributing to the total signal V=R₁I+R₂I². All measurements are at room temperature, unless otherwise noted.

Figure 2: Sample geometry and non-local measurement configuration.

a, Coloured scanning electron microscopy image of the device (after measurement and sample failure). Tunnel contacts have electrodes made of 5/25-nm-thick Ti/Au (contacts 1, 4 and 5) or 30-nm-thick Co (contacts 2 and 3). Upper inset: Optical image before measurement. Lower inset: Atomic force microscopy image of graphene before contact deposition. b, Configuration for measuring linear spin resistance using a magnetic detector. c, Configuration for measuring nonlinear resistance using non-magnetic detectors.

We start by characterizing spin transport in the linear regime. The results in Fig. 3 show a non-local spin-valve effect, demonstrating spin transport between contacts 2 and 3, for a centre-to-centre separation of L=1.0 μm and width of graphene w≈1.1 μm. The obtained spin resistance ΔR₁≈4 Ω is nearly constant versus the gate voltage V_g applied to the substrate. V_gcontrols the charge-carrier density n_g in graphene as n_g=γ(V_g−V_D), with V_D the condition for charge neutrality (Dirac point) and γ=7.2×10¹⁴ m⁻² V⁻¹. On the other hand, the graphene square resistance R_sq depends on V_g, changing by a factor of five. The observed ΔR₁ versus R_sq behaviour can be understood by the standard relation¹⁵ ΔR₁=(P²R_sqλ/w)exp(−L/λ), with P the spin polarization of the magnetic contacts, as being due to the charge-carrier-density dependence of λ with a minimum at the Dirac point. The latter is given by the behaviour of the spin-diffusion constant D and spin-relaxation time τ in graphene^19,20,21 (Supplementary Section SA). Furthermore, the previous relation is valid only for contact resistances R_c≫R_sqλ/w, where the contacts do not affect the spin transport^16,17,22. We take into account both considerations in our modelling below, by parameterizing λ (Fig. 3d) and by including the finite resistance of the contacts used for spin injection and detection.

Figure 3: Linear spin detection using a magnetic detector.

a, Spin-valve effect in non-local linear resistance R₁ by sweeping an in-plane magnetic field at V_g=0 V. Two well-defined values correspond to parallel (R₁^Pa) and antiparallel (R₁^Ap) alignment of Co contacts. b, Spin resistance ΔR₁=R₁^Pa−R₁^Ap versus V_g. The dashed line is the square resistance R_sq of graphene between contacts 2 and 3 with V_D≈−20 V. c, Hanle spin-precession curve by sweeping a perpendicular magnetic field at V_g=10 V. The solid line is a fit with the one-dimensional Bloch equation. The obtained parameters are D=0.025 m² s⁻¹ and τ=71 ps, with contact spin polarization P=9%. d, Spin-relaxation length , with D and τ extracted from Hanle curves taken at several values of V_g. The solid line is a fit with a Gaussian function for parameterization purposes.

Next, we demonstrate nonlinear detection of spins by using non-magnetic contacts. In Fig. 4b is shown a clear spin-valve effect in the second-order component V₂ of the non-local signal. The transitions in V₂ occur at the switching fields of the magnetic contacts used for current injection. We observe at zero gate voltage that V₂^Ap>V₂^Pa, consistent with the presence of a larger Δμ for the antiparallel magnetic configuration¹⁵ and a positive sign of the parameter α for electron transport¹². Therefore, we expect that the sign of the nonlinear spin resistance ΔR₂ should follow that of α and change sign when going from transport in the electron (V_g>V_D) to the hole (V_g<V_D) regime. The latter is confirmed by observing that ΔR₂<0 for gate voltages V_g≪V_D. We remark that the measured spin-valve signal cannot be explained by spurious detection of potentials in the current-carrying part of the sample, owing to the absence of spin-valve signal in the first-order response (Fig. 4a).

Figure 4: Nonlinear spin detection using non-magnetic detectors.

a, Linear non-local signal versus in-plane magnetic field; no spin-valve effect is observed. b, Second-order signal (same measurement as in a) showing spin-valve effect. Two well-defined values correspond to parallel (V₂^Pa) and antiparallel (V₂^Ap) alignment of the Co contacts. Curves in a and b correspond to (from top to bottom) V_g=30,0,−40,−80 and −90 V and are offset vertically for clarity. Each curve is the average of ten measurements. All data are for a root-mean-square current of 5 μA (configuration as in Fig. 2c). c, Nonlinear spin resistance ΔR₂=R₂^Ap−R₂^Pa versus V_g. For each data point the average value of V₂ for (anti)parallel configuration, and its standard deviation, was extracted from curves such as those shown in b. The solid line is a result from numerical modelling.

The gate-voltage dependence of the nonlinear spin resistance is presented in Fig. 4c. The ΔR₂ versus V_g curve shows a maximum of ≈5 k Ω A⁻¹ for electron transport. We did not observe a clear sign change when crossing the Dirac point, whereas for hole transport there was a minimum value of only ≈−2 kΩ A⁻¹. To understand this electron–hole asymmetry we looked into the charge-transport properties of the detector circuit, between contacts 4 and 5. The Dirac curve in Fig. 5a shows that, while there is a reasonable symmetry for V_g close to V_D=−9 V, this is not the case for larger V_g, as shown by the kink visible at V_g=−55 V. Such kinks in the Dirac curve have been described as arising owing to electron doping from metal contacts with a thin oxide layer that prevents charge-density pinning²³. Our contacts are deposited onto a thin oxide barrier. Therefore, we interpret the Dirac curve of the detector circuit as being composed of two contributions, the graphene under (and next to) the contacts and that away from the contacts (curves 1 and 2 in Fig. 5a, Supplementary Section SB).

Figure 5: Role of charge-density distribution.

a, Resistance of graphene between contacts 4 and 5 (Au detectors). The red solid line is a fit using a phenomenological description including two Dirac curves (solid lines labelled 1 and 2) and a constant 0.35 kΩ for the low-resistance contact 5 (dashed line). b, Extracted parameter α=σ⁻¹∂ σ/∂ ε for each of the two Dirac curves mentioned in a. c, Schematic representation of charge-density distribution within graphene. Different properties are considered for graphene under and next to the contacts (1) and for the region away from the contacts (2).

Having described both spin and charge transport in the linear regime, we now construct a minimal one-dimensional model that enables quantitative comparison with experiment. As mentioned above, we model Δμ by considering the induced conductivity spin polarization β, finite-resistance contacts and gate-voltage dependence of λ. We use a fixed P=9% for the magnetic contacts (extracted in the regime R_c≥5R_sqλ/w) and a width profile for graphene as extracted from atomic force microscopy. Furthermore, we describe the Dirac curve for each graphene region using the approximate relation²⁴σ=ν e(n_g²+n_i²)^1/2, with ν the carrier mobility and n_i a background carrier density due to the presence of electron–hole puddles and thermally generated carriers. We then extract the parameter α for each region¹² (Fig. 5b) in a similar way to the extraction of the Seebeck coefficient of graphene from the Dirac curve ^14,24.

The model, schematically shown in Fig. 5c, has the extension of the graphene region 1 beyond the contact edge as the only free parameter. Scanning photocurrent work²⁵ has shown that the doping in graphene decays gradually from the contact edge, extending up to a distance of ≈0.3 μm. For simplicity we consider a constant doping up to a distance of 0.15 μm. The modelled ΔR₂-versus- V_g curve (solid line in Fig. 4c) successfully reproduces both the trend and the magnitude of the data. The agreement imparts certainty to our interpretation of the measured ΔR₂ signal as arising owing to the nonlinear interaction between spin and charge.

The magnitude of ΔR₂ is only slightly limited by the finite resistance of our contacts (R_c≈7 kΩ). Assuming infinite contact resistance, we predict only up to a twofold increase in ΔR₂. On the other hand, the use of high-quality tunnel contacts²² with P=30% would yield a tenfold increase. Moreover, as , similar to the Seebeck coefficient¹⁴, decreasing n_i by two orders of magnitude by using a boron nitride substrate²⁶ would yield a further tenfold increase. Therefore, the herewith demonstrated effect is a real candidate for spin detection. It can be regarded as a step in the logical progression from linear interactions between spin and charge towards interactions between spin and heat, as studied in the field of spin caloritronics²⁷.

Methods

Sample preparation.

Graphene is obtained from highly oriented pyrolytic graphite by mechanical exfoliation and deposited on a highly n-doped Si substrate covered with a thermal oxide layer 300 nm thick. The Si substrate is used as electrostatic gate. Graphene is first covered by 0.8 nm Al followed by natural oxidation to obtain a thin aluminium oxide layer. Electron-beam lithography, deposition by evaporation and lift-off were carried out twice, first for the Ti/Au contacts and then for Co. We observed in previous samples a lower resistance of the Ti/Au contacts, which prevented us from using them for spin detection¹⁶. This problem was possibly related to the required baking of poly(methyl methacrylate) for the second electron-beam lithography step, which may cause diffusion of Ti/Au through the oxide barrier. To solve it we increased the thickness of the oxide barrier only for the Ti/Au contacts by deposition and oxidation of an extra 0.3 nm of Al. This yielded non-invasive Au contacts with similarly high resistances to those of the Co contacts.

Measurements.

Characterization took place at room temperature and at 77 K (Supplementary Section SA) in a cryostat with a base pressure ≈1×10⁻⁷ mbar. The sample was first annealed under vacuum at 130 °C for ≈24 h for removal of physisorbed water, resulting in low hysteresis in the Dirac curve (ΔV_D<10 V). This hysteresis leads to the increased uncertainty of ΔV₂ around V_g=−20 V seen in Fig. 4c. Measurements were made using a 1–5 μA a.c. current source and recording simultaneously the first- and second-harmonic responses using two lock-in systems. All current and voltage signals reported are root-mean-square values. Therefore, the resistances were extracted as R₁=V₁/I and . Excitation frequency was kept at ≤3 Hz to prevent signals due to capacitive coupling, as determined by frequency scans. Contribution from higher harmonics was found to be negligible.

Modelling.

We developed a one-dimensional finite-element code using the program MATLAB to find numerical solutions for the two-channel spin diffusion equations¹³

with the inclusion of an element-specific conductivity spin polarization¹²β, as described in the main text. Element length was kept ≤10 nm. I_± and Δμ were set to be continuous across element boundaries. We consider point contacts located at the centre of the fabricated electrodes, which could either inject a spin current P I or detect the electrochemical potential μ_avg+PΔμ. Spin relaxation under contacts with finite resistance (4.9, 9.2, 7.3 and <1 kΩ for contacts 2, 3, 4 and 5, respectively) was implemented as in ref. 17, with the extra consideration of contact spin polarization P. We use a phenomenological description of each Dirac curve by the relation σ=ν e(n_g²+n_i²)^1/2, which describes the data using a constant mobility ν by including the effect of electron–hole puddles through a background carrier density n_i (ref. 24). For each Dirac curve the parameter α=σ⁻¹∂ σ/∂ ε is extracted using ∂ σ/∂ ε=(∂ σ/∂ n_g)(∂ n_g/∂ ε), in a manner similar¹² to that used in the literature for the Seebeck coefficient^14,24. The extracted parameters for the curve Dirac 2 (graphene between contacts) were ν=3,900 cm² V⁻¹ s⁻¹ and n_i=3.5×10¹⁵ m⁻², consistent with previous experiments on SiO₂ substrates²⁴, whereas for Dirac 1 we obtained ν=800 cm² V⁻¹ s⁻¹ and n_i=2×10¹⁶ m⁻². To obtain ΔR₂ we calculated the difference in potential V=−μ_avg/e between the Au detectors, for both parallel and antiparallel configurations and d.c. currents I=±5 μA. The result was then fitted with ΔV =ΔR₁I+ΔR₂I². The odd contribution |ΔR₁|<3 mΩ was found to be negligible.