Dynamical d-wave condensation of exciton–polaritons in a two-dimensional square-lattice potential

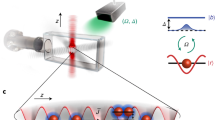
Abstract

Macroscopic order appears as the collective behaviour of many interacting particles. Prime examples are superfluidity in helium¹, atomic Bose–Einstein condensation², s-wave³ and d -wave superconductivity⁴ and metal–insulator transitions⁵. Such physical properties are tightly linked to spin and charge degrees of freedom and are greatly enriched by orbital structures⁶. Moreover, high-orbital states of bosons exhibit exotic orders distinct from the orders with real-valued bosonic ground states⁷. Recently, a wide range of related phenomena have been studied using atom condensates in optical lattices^8,9,10, but the experimental observation of high-orbital orders has been limited to momentum space^11,12. Here we establish microcavity exciton–polariton condensates as a promising alternative for exploring high-orbital orders. We observe the formation of d -orbital condensates on a square lattice and characterize their coherence properties in terms of population distributions both in real and momentum space.

Main

Exciton–polaritons emerge from the strong light–matter coupling in semiconductor quantum wells embedded in a planar microcavity structure. They behave as degenerate Bose gases in the low-density and low-temperature limit¹³. Exciton–polaritons have undergone a dynamic phase transition, in which a macroscopic number of particles are accumulated in the lowest-energy single-particle state with a long-range order^14,15,16,17. Owing to their very light effective mass, the phase transition temperatures of exciton–polaritons are eight to nine orders of magnitude higher than those of atomic Bose–Einstein condensates. Coherence properties of exciton–polariton condensates have been characterized by the direct optical access in spatial and momentum spaces^14,15,16,18.

Modern solid-state physics has studied quantum many-body phenomena whose properties reflect exotic orbital nature, another intrinsic degree of freedom, which interplays with charge and spin degrees of freedom. Its energy degeneracy and spatial anisotropy generate rich dynamics in weakly interacting many-body systems. For example, a key role of d -orbital nature has been actively investigated in salient phenomena including metal–insulator transitions⁵, colossal magnetoresistance^6,19, and recently discovered iron-pnictide superconductors^20,21. These orbital ordering phenomena originate from the strong correlation effects of electrons in the anisotropic degenerate d -orbitals. Theoretical modelling of such phenomena is beyond the single orbital band picture and necessarily complicated. As high-orbital bosonic condensate states can exhibit unconventional quantum order distinct from those induced by the conventional many-body ground-state wavefunctions beyond Feynman’s no-node theorem^7,22, the formation of designated high-orbital condensate states would pave a way to investigate exotic quantum order. Recently, a p -orbital condensate using ultracold atoms in an optical lattice has been prepared²³; however, to the best of our knowledge, a d -orbital condensate in the atom–optical lattice system has not yet been realized because of experimental difficulties. On the other hand, high-orbital bosonic condensates in the p - and d -orbital states are readily accessible in exciton–polariton systems through the bottleneck condensation dynamics by controlling the polariton density. Anti-phased p -orbital condensates were first demonstrated in a one-dimensional condensate array analogous to a Josephson π -junction array¹⁸, and the condensates in excited states are created in a single trap potential naturally induced by an impurity or disorder²⁴ or in a micropillar trap potential²⁵. Here we present our first demonstration of coherent anti-phased d -orbital condensates formed in a two-dimensional square-lattice potential. The direct natural leakage of the photons out of the microcavity allows real-space and momentum-space spectroscopy of the d -orbital order.

Our two-dimensional (2D) square-lattice device is patterned by depositing a thin metal film on top of a AlGaAs/AlAs planar microcavity wafer containing 12 GaAs quantum wells at the three central antinodes. The potential depth induced by the metal film is ∼200 μeV near zero detuning^18,26 (see Methods for details on the device preparation and experimental set-up). We present our experimental results with a 2D square-lattice device with a=4 μm near zero detuning (∼−0.5 meV). We examine the spatial and the momentum distribution of microcavity exciton–polaritons in this periodic lattice potential at liquid He temperatures (∼4 K). We excite the system using a mode-locked Ti:sapphire laser in a pulsed scheme, resonant to the excitonic branch at an energy (∼767.7 nm) ∼6 meV higher than the energy of the polariton ground state with k_∥∼7.39 ×10⁴ cm⁻¹∼5(2π/a), ten times larger than the momentum values of the first Brillouin zone edges (±π/a). We collect time-averaged lower polariton emission, and the far-field spectroscopy reveals the lower polariton energy–momentum dispersion curve, and the far-field imaging directly maps the Brillouin zones of the reciprocal Bravais lattices.

The estimated kinetic energies at the boundaries of the first Brillouin zone, X and M points, are K_X(k_∥=±(π/a))∼260 μeV and with an effective mass of a polariton m^*∼9×10⁻⁵m₀ (m₀ is the bare electron mass) and a=4 μm. A square lattice, one of the simplest 2D lattice structures, holds translational, rotational and reflection symmetry. The reciprocal Bravais lattice is also a square pattern with a unit length 2π/a. The band structures (Fig. 1b) and the 2D Brillouin zones (Fig. 1c) of a single particle with an effective mass m^* are computed with the standard plane-wave bases²⁷. Figure 1c illustrates the first four Brillouin zones, where three high-symmetry points (Γ, X, M) are specified. Experimental far-field images at a pump rate above the condensation threshold clearly identify these Brillouin zones for the 4 μm-period square lattice (Fig. 1d). Whereas both Γ and M points exhibit four-fold rotational symmetry, X points exhibit two-fold symmetry. At these high-symmetry points, the eigenstates can be classified according to their symmetry properties of the rotation group analogous to atomic orbital state denotation. At the Γ point, the lowest-energy ground state exhibits non-degenerate 1s -wave symmetry, and the next excited (quartet) states are denoted by $3d_{x^2-y^2}$,2p_x,2p_y and 2s -wave symmetries in real space. It is expected that the equilibrium condensation takes place with this 1s -wave symmetry at the Γ point. Similarly, the lowest-energy (quartet) states at the M point are split into 3d_{x y},2p_x,2p_y and 1s —states for which the 3d_{x y}-wave state is only metastable, and thus it is expected that the dynamic condensation occurs with the 3d_{x y}-wave symmetry at the M point. Finally, the lowest-energy (doublet) states at the X point are 2p_x (or 2p_y) and 1s states, for which the 2p_x (or 2p_y) state is only metastable as a candidate for the dynamic condensation at X points.

Figure 1: Two-dimensional square-lattice device, band structure and Brillouin zones.

a, Photograph of a 2D square-lattice structure of metal films on top of an AlGaAs/AlAs planar microcavity. A square lattice is formed by the array of circular apertures whose diameter is half the size of the lattice period a . The arrows represent the unit vectors, . b, The band structure of a periodic 2D square-lattice potential assuming V ₀=0.2E₀, where V ₀ and E₀ are the confining potential energy and the ground-state kinetic energy. c, Theoretical Brillouin zones of the 2D square lattice. d, Experimental far-field pattern corresponding to the Brillouin zones of c. The axis orientations of are given by the arrows. The dashed lines labelled 1 and 2 indicate the measurement axes for the energy–momentum dispersion (see the text). The colour scale bar shows the photoluminescence intensity strength from low (blue) to high (red) values.

Figure 2a shows the observed far-field images in momentum (k_∥,x, k_∥,y) space at various optical pump powers. These images are taken under the pump direction of ( are momentum space unit vectors of the configuration in Fig. 1d). This particular pump direction was chosen to access energy values of s, p and d_{x y} states individually from spectrometer measurements. Exciton–polaritons are injected at a fixed wavenumber k_p∼7.39×10⁴ cm⁻¹ (∼5(2π/a)) even far outside the first Brillouin zone edges indicated by the red arrow in Fig. 2a. We clearly observe that different momentum distributions of exciton–polaritons emerge in a distinct order with increasing injected particle density. Below the condensation threshold pump power (P<P_th∼7 mW), isotropic thermal lower polaritons leak as photons at finite |k| values ∼(2π/a) before they relax to the ground state at (k_∥,x,k_∥,y)∼0, giving a doughnut-shaped emission pattern (bottleneck effect). Near the condensation threshold pump power P∼P_th, the metastable 3d_{x y} state at M points, , of the first Brillouin zone is selectively occupied as expected. The injected exciton–polaritons with the initial momentum relax anddynamically condense at M points. As the pump rate increases, the momentum spread Δk at M points markedly decreases, indicating that a phase order is formed over a macroscopic distance ∼40 μm. With a further increase of the pump rate, the condensation in the metastable 2p_x state at X points and finally the condensation in the 1s ground state at the Γ point are observed. The crossover behaviour among the 3d_{x y}, 2p_x and 1s states for varying pump rates is presented in Fig. 2b. As our initial laser momentum is ten times larger than the first Brillouin zone edge, a significant incoherent scattering process by acoustic phonons should be involved to relax into the first Brillouin zone. Consequently, the coherence of the d - and p -band is established spontaneously. Figure 2c shows that this dynamical competition among states is well captured by a simple theoretical model using the coupled rate equations with a reasonable decay rate of an individual state.

Figure 2: Lower polariton distribution in reciprocal lattice space.

a, Pump-power-dependent far-field images for the pumping direction along . The relative pump rates (P/P_th) are 0.29, 1, 1.7, 4.3 and 29. The narrow peaks in the square-lattice positions originate from pump laser scatterings by the periodic circular aperture, whose distance provides the size of the first Brillouin zone, 2π/a (white bar), empirically with a 0.5% error due to the difference in the laser wavelength and polariton wavelength. b, The population of 1s,2p_x and 3d_{x y} -orbital states plotted against the pump power. c, Numerical simulation results of integrated lower polariton photoluminescence intensity of the 1s, 2p_x and 3d_{x y} -orbital states against the normalized pump power.

The far-field interference patterns manifest the relative phase between the real-space Bloch wavefunctions of the orbital symmetry. We compute the real-space wavefunction configurations (near-field images) and the momentum distribution (far-field images). Figure 3 shows the strong parabolic trap potential case in a 3-by-3 lattice site, where real-space wavefunctions are tightly localized at each site, which elucidate clearly the near-field orbital symmetry (the near-field wavefunctions and the far-field distribution in a weak trap potential case, which are more relevant to our experimental condition, are presented in the Supplementary Information). The 1s ground state is stable at the Γ point, the metastable 2p_x states appear at X points and the metastable 3d_{x y} states appear at M points. The anti-phased 3d_{x y} -orbital symmetry between nearest-neighbour sites is the reason for the intensity peaks at M points in momentum space in Fig. 3c. Similarly, the anti-phased 2p_x states are responsible for the intensity peaks at X points in Fig. 3b. On the other hand, the conventional in-phased 1s -orbital condensate produces the intensity peak at the Γ point in Fig. 3a. Multiple side peaks in the far-field patterns in Fig. 3 arise from the tightly localized wavefunction per site in the strong potential case, whereas only the first-order interference peaks appear in the weak potential case (Supplementary Information). In our experimental results presented in Fig. 2a, the interference patterns created by the 1s and 2p_x orbitals are broader in momentum space compared with that created by the 3d_{x y} orbitals. This feature implies that the 1s and 2p_x orbitals are less coherent than the 3d_{x y} orbitals in real space. This is a direct consequence of the larger tunnelling coupling between sites for the 3d_{x y} state.

Figure 3: Theoretical near-field and far-field patterns in a strong potential.

The calculation assumed a strong harmonic potential trap, and the near-field (top) and far-field (bottom) wavefunctions for the 1s (a), 2p_x (b) and 3d_{x y} (c) orbital condensates are presented, where the red (blue) colour indicates positive (negative) amplitudes in real-space wavefunctions. The positions of circular traps (apertures) on the device surface are indicated by dotted circles. Whereas 1s -orbital wavefunctions are connected in-phase between lattice sites, both 2p_x and 3d_{x y} wavefunctions are connected in an anti-phased manner. The square of the far-field wavefunction or the momentum distribution of the three condensates is also shown. The anti-phased 2p_x,3d_{x y} wavefunctions in real space induce interference peaks at the X and M points, respectively, in momentum space. The calculation results in the case of the weak trap potential are given in the Supplementary Information.

To quantify the energy eigenvalues of the three orbital states, we carry out the spectroscopic measurement of the energy–momentum dispersion relation by selecting a particular cross-section in momentum space (Fig. 4a,b). Selected cross-sections are along the lines indicated by diagonal lines with numbers 1 and 2 in Fig. 1d. The 1s and 3d_{x y} orbitals are observed in line 1, whereas only the 3d_{x y} orbital is observed in line 2. From the pump-power dependence of the observed energy–momentum dispersion curves, we extract two quantities: the energy eigenvalues and the 2D in-plane wavenumbers of individual orbital states. Along line 1, the distance between two prominent peaks (3d_{x y} -orbital states) corresponds to the diagonal length of the first Brillouin zone , and the energy of these states lies at E_{3d x y}(M)∼1,610.55 meV near the threshold pump, P_th,d=7 mW (Fig. 4a, left). The 1s ground-state energy at (k_∥,x,k_∥,y)=(0,0) is E(0)∼1,608.93 meV below the condensation threshold, but this s-orbital state also condenses at E_s(0)∼1,609.83 meV at the slightly higher threshold power P_th,s=10 mW. An energy blueshift (∼0.9 meV) is due to the repulsive polariton–polariton interactions. The E_{3d x y}(M) at line 2 is identical to that of the 3d_{x y} state along line 1 (Fig. 4a, right) as expected. Near the threshold pump power, the energy eigenvalues of the 1s state at the Γ point, 2p_x state at X points, and 3d_{x y} states at M points are equally spaced by 0.36 meV, which is compatible with the theoretically expected energy spacing ∼0.26 meV within 30% error. At higher pump power, lower polaritons at high-orbital states are further relaxed into smaller k_∥ -valued states, and Fig. 4b shows some representative data at P∼50 mW∼7P_th .

Figure 4: Energy-momentum dispersion characteristics.

The cross-sectional energy–momentum dispersion relations are measured along lines 1 and 2 in Fig. 1d. Line 1 (left column) follows the high-symmetry point Γ–M direction of the first Brillouin zone and line 2 (right column) examines the edge of the second Brillouin zone around the M point. Experimental data are taken at P/P_th=1 (P_th=7 mW; a) and P/P_th∼7 (b), presented on a linear intensity scale. Along line 1, we have extracted the energy values and the population of the 1s and 3d_{x y} condensate states in terms of the pump power. The same information for the 2p_x condensate states between lines 1 and 2 is presented in Supplementary Fig. S2. The nonlinear increases for 1s, 2p_x and 3d_{x y} condensate populations are given in Fig. 2c. Distinct signals from M points along line 2 in b appear even at high power values, whereas the dominant 1s condensate signals mask the signals at M points along line 1 in b.

We execute spatially resolved spectroscopy and capture the near-field images, from which the 3d_{x y}-orbital condensation is confirmed. The cross-sectional cuts at two energy eigenvalues (s (blue) and d (red) orbitals) along the direction ( are real-space unit vectors of the configuration in Fig. 1a) show the anti-correlated emission profiles in spatial coordinates for the 1s -orbital condensate and 3d_{x y} -orbital condensates (Fig. 5a). A similar result is obtained along the direction, which unambiguously confirms the 3d_{x y} symmetry of the real-space Bloch wave. Phase coherence of the 3d_{x y} -orbital condensate is further confirmed by a Michelson interferometer constructed in momentum space. We place a simple mirror and a right-angle prism at each arm of the Michelson interferometer to fold the far-field images with respect to the centre line. Figure 5b shows that the interference fringes indeed exist only at M points near P∼P_th. This result rules out the independent condensation at four M points (condensate fragmentation in momentum space) but supports our previous discussion that the dynamic condensation takes place with the anti-phased 3d_{x y}-wave symmetry over many sites.

Figure 5: Energy-resolved spatial characteristics.

a, Cross-sectional intensity profile at two energy eigenvalues, 1,609.64 meV (3d_{x y} orbital, red) and 1,608.76 meV (1s orbital, blue). b, Interference fringe at P/P_th=1 observed in a far-field plane from Michelson interferometry, in which one arm has a standard mirror and the other has a right-angle prism for folding an image along the centre (dashed line).

Methods

Sample preparation.

Our wafer is grown by molecular beam epitaxy on a (100)-oriented GaAs substrate. We have placed three four-fold stacks of 7-nm-thick quantum wells separated by 3-nm-thick AlAs barriers at the three central antinodes of the microcavity. The wafer displays an exciton–polariton splitting of ∼13.6 meV at zero detuning, and the cavity resonance energy is tapered for the detuning parameter adjustment. An electrostatic in-plane trap potential in a 2D square-lattice geometry is produced by depositing a thin Au/Ti (25/3 nm) film on a lithographic pattern (Fig. 1a). The pattern arranges circular apertures with a period of a, where a/2 is the diameter of the aperture.

Experimental set-up.

The sample was optically pumped by a mode-locked Ti:sapphire laser, focused to a 60-by-120 μm² spot. A circularly polarized 3 ps pulse is injected at an incident angle of 60° (corresponding to the in-plane wavenumber, k_∥∼7.39×10⁴ cm⁻¹∼5(2π/a)) with a 76 MHz repetition rate. We collect time-averaged lower polariton emission through a 0.55 NA microscope objective lens, fed into either a 750 mm grating spectrometer with a nitrogen–cooled CCD (charge-coupled device) for spectroscopy or a CCD camera for imaging.